Note：[ wechat：Y466551 | 可加勿騷擾，付費諮詢 ]

論文資訊

論文標題：WIND: Weighting Instances Differentially for Model-Agnostic Domain Adaptation
論文作者：
論文來源：2021 ACL
論文地址：download 
論文程式碼：download
視屏講解：click

1 介紹

　　出發點：傳統的範例加權方法由於不能學習權重，從而不能使模型在目標領域能夠很好地泛化；

　　方法：為了解決這個問題，在元學習的啟發下，將領域自適應問題表述為一個雙層優化問題，並提出了一種新的可微模型無關的範例加權演演算法。提出的方法可以自動學習範例的權重，而不是使用手動設計的權重度量。為了降低計算複雜度，在訓練過程中採用了二階逼近技術；

　　貢獻：

• • 提出了一種新的可微範例加權演演算法，該演演算法學習梯度下降範例的權重，不需要手動設計加權度量；
  • 採用了一種二階近似技術來加速模型的訓練；
  • 對三個典型的NLP任務進行了實驗：情緒分類、機器翻譯和關係提取。實驗結果證明了該方法的有效性；

2 相關

　　事實：把域外、域內資料聯合訓練做領域適應，但並不是所有來自域外資料集的樣本在訓練過程中都具有相同的效果。一些關於神經機器翻譯（NMT）任務的研究表明，與域內資料相關的域外範例是有益的，而與域內資料無關的範例甚至可能對翻譯質量有害 。

　　目前的實列加權方法：

• • 核心思想：根據範例的重要性以及與目標域的相似性來加權範例；
  • 問題：當前領域適應場景中，域外語料庫的規模大於域內語料庫，容易導致學習到的權值偏向於域外資料，導致域內資料的效能較差；

3 方法

 　　為避免域內資料的效能較差，如何有效地利用 $\mathcal{D}_{\text {in }}$ 是域轉移的關鍵。為解決這個問題，首先從 $\mathcal{D}_{\text {in }}$ 中抽取子集 $\mathcal{D}_{i t}=\left\{\left(x_{i}, y_{i}\right)\right\}_{i=1}^{n_{1}}$，併為每個範例 $\left(x_{i}, y_{i}\right) \in \mathcal{D}_{i t} \cup \mathcal{D}_{\text {out }}$ 分配一個標量權值 $w_{i}$。本文希望在訓練過程中，模型能夠找到最優的權重 $\boldsymbol{w}=\left(w_{1}, \ldots, w_{n_{1}+m}\right)$，因此，權重 $w$ 是可微的，並可通過梯度下降優化。此外，將 DNN 表示為由 $\theta$ 引數化的函數 $f_{\theta}: \mathcal{X} \rightarrow \mathcal{Y}$，並將 $x_{i}$ 從輸入空間對映到標籤空間。

　　最終訓練損失遵循一個加權和公式：

　　　　$\mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})=\frac{1}{n_{1}+m} \sum_{\substack{\left(x_{i}, y_{i}\right) \;\in \; \mathcal{D}_{i t}\; \cup\; \mathcal{D}_{\text {out }}}} \; w_{i} \ell\left(f_{\boldsymbol{\theta}}\left(x_{i}\right), y_{i}\right)$

　　其中 $\ell$ 表示損失函數，可以是任何型別的損失，如分類任務的交叉熵損失，或標籤平滑交叉熵損失。

　　由於域內和域外資料集的資料分佈存在差異，簡單聯合優化 $\boldsymbol{\theta}$ 和 $\boldsymbol{w}$ 可能會對 $\boldsymbol{w}$ 引入偏差。本文期望在 $\boldsymbol{w}$ 上訓練的模型可以推廣到域內資料。受 MAML 的啟發，本文建議從 $\mathcal{D}_{i n}$ 中取樣另一個子集 $\mathcal{D}_{q}=\left\{\left(x_{i}, y_{i}\right)\right\}_{i=1}^{n_{2}}$ 命名為查詢集，使用這個查詢集來優化 $\boldsymbol{w}$。具體來說，目標是得到一個權重向量 $w$ 減少 $\mathcal{D}_{q}$ 上的損失：

　　　　$\mathcal{L}_{q}(\boldsymbol{\theta})=\frac{1}{n_{2}} \sum_{\left(x_{i}, y_{i}\right) \in \mathcal{D}_{q}} \ell\left(f_{\boldsymbol{\theta}}\left(x_{i}\right), y_{i}\right)$

　　總結：隨機初始化 $\boldsymbol{w}$，用 $\mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})$ 訓練一個模型，得到優化後的引數 $\boldsymbol{\theta}^{*}$，接著固定 $\boldsymbol{\theta}^{*}$ ，最小化在查詢集上的損失，得到新的 $\boldsymbol{w}$。

　　該過程表述為以下雙層優化問題：

　　　　$\begin{array}{ll}\underset{\boldsymbol{w}}{\text{min}}& \mathcal{L}_{q}\left(\boldsymbol{\theta}^{*}\right) \\\text { s.t. } & \boldsymbol{\theta}^{*}=\underset{\boldsymbol{\theta}}{\arg \min }\; \mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})\end{array}$

　　上述雙層優化問題由於求解複雜性高，難以直接解決。受 MAML 中的優化技術啟發，將每次迭代的訓練過程分為以下三個步驟：

• 偽更新

　　　　$\widehat{\boldsymbol{\theta}}=\boldsymbol{\theta}-\beta \cdot \nabla_{\boldsymbol{\theta}} \mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})$

• 範例權重更新

　　　　$\begin{aligned}\boldsymbol{w}^{*} & =\underset{\boldsymbol{w}}{\arg \min } \mathcal{L}_{q}(\widehat{\boldsymbol{\theta}}) \\& =\underset{\boldsymbol{w}}{\arg \min } \mathcal{L}_{q}\left(\boldsymbol{\theta}-\beta \cdot \nabla_{\boldsymbol{\theta}} \mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \boldsymbol{w})\right)\end{aligned}$

　　　　$\widehat{\boldsymbol{w}}=\boldsymbol{w}-\gamma \cdot \nabla_{\boldsymbol{w}} \mathcal{L}_{q}(\widehat{\boldsymbol{\theta}})$

• 最終更新

　　　　$\boldsymbol{\theta} \leftarrow \boldsymbol{\theta}-\beta \cdot \nabla_{\boldsymbol{\theta}} \mathcal{L}_{\text {train }}(\boldsymbol{\theta}, \widehat{\boldsymbol{w}})$

　　對 $\nabla_{\boldsymbol{w}} \mathcal{L}_{q}(\widehat{\boldsymbol{\theta}})$ 使用鏈式法則：

　　　　$\begin{aligned}\widehat{\boldsymbol{w}} & =\boldsymbol{w}-\gamma \cdot \nabla_{\boldsymbol{w}} \mathcal{L}_{q}(\widehat{\boldsymbol{\theta}}) \\& =\boldsymbol{w}-\gamma \cdot \nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \cdot \nabla_{\boldsymbol{w}} \widehat{\boldsymbol{\theta}} \\& =\boldsymbol{w}+\beta \gamma \cdot \nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \cdot \nabla_{\boldsymbol{\theta}, \boldsymbol{w}}^{2} \mathcal{L}_{\text {train }}\end{aligned}$

　　問題：使用 $|\boldsymbol{\theta}|$，$|\boldsymbol{w}|$ 分別表示 $\boldsymbol{\theta}$，$\boldsymbol{w}$ 的維數，二階推導 $\nabla_{\boldsymbol{\theta}, \boldsymbol{w}}^{2} \mathcal{L}_{\text {train }}$ 是一個 $|\boldsymbol{\theta}| \times|\boldsymbol{w}|$ 矩陣，無法計算和儲存。幸運的是，可採用 DARTS 中使用的近似技術來解決這個問題，這種技術使用了有限差分近似：

　　　　$\begin{array}{c}\nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \cdot \nabla_{\boldsymbol{\theta}, \boldsymbol{w}}^{2} \mathcal{L}_{\text {train }} \approx \frac{\nabla_{\boldsymbol{w}} \mathcal{L}_{\text {train }}\left(\boldsymbol{\theta}^{+}, \boldsymbol{w}\right)-\nabla_{\boldsymbol{w}} \mathcal{L}_{\text {train }}\left(\boldsymbol{\theta}^{-}, \boldsymbol{w}\right)}{2 \epsilon} \\\boldsymbol{\theta}^{+}=\boldsymbol{\theta}+\epsilon \nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \\\boldsymbol{\theta}^{-}=\boldsymbol{\theta}-\epsilon \nabla_{\widehat{\boldsymbol{\theta}}} \mathcal{L}_{q} \\\end{array}$

演演算法

4 實驗結果

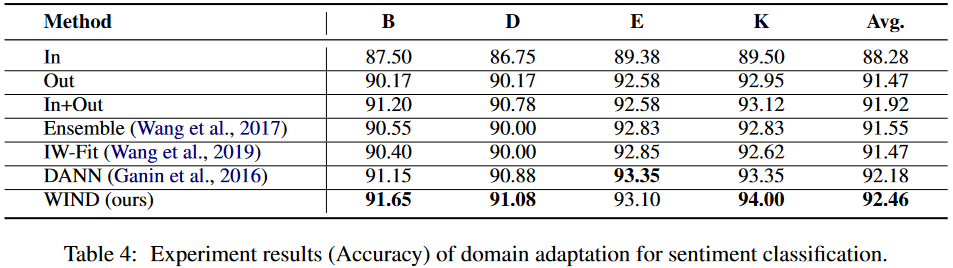
情感分析