「學習筆記」擴充套件 KMP(Z 函數)
對於個長度為 \(n\) 的字串 \(s\)。定義 \(z[i]\) 表示 \(s\) 和 \(s[i,n-1]\)(即以 \(s[i]\) 開頭的字尾)的最長公共字首(LCP)的長度。\(z\) 被稱為 \(s\) 的 Z 函數。這裡注意,在 Z 函數中,\(z[0] = 0\),但是根據 LCP 的定義,\(z[0] = n\),具體應該為何值,根據題目意思來判斷。本文更偏向根據 LCP 的定義來確定 \(z[0]\) 的值
演示
對於字串 \(\texttt{aaaaaaaba}\),它的 Z 函數是這樣的。
過程
我們設現在 \(i + z[i] - 1\) 的最大值為 \(r\),得到這個最大值的 \(i\) 為 \(l\)。

假設我們現在要求 \(z[x]\),\(z[0, x - 1]\) 已經求出來了,現在,讓我們分類討論各種情況。
-
當 \(x \le r\) 時
如圖所示,
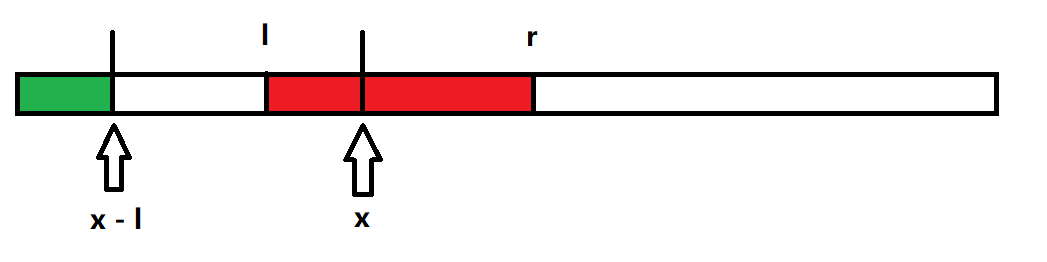
因為 \(s[l, r]\) 等於 \(s[0, r - l]\),所以 \(s[l, x] = s[0, x - l]\),對應到下圖,就是綠色區域和黃色區域相同。
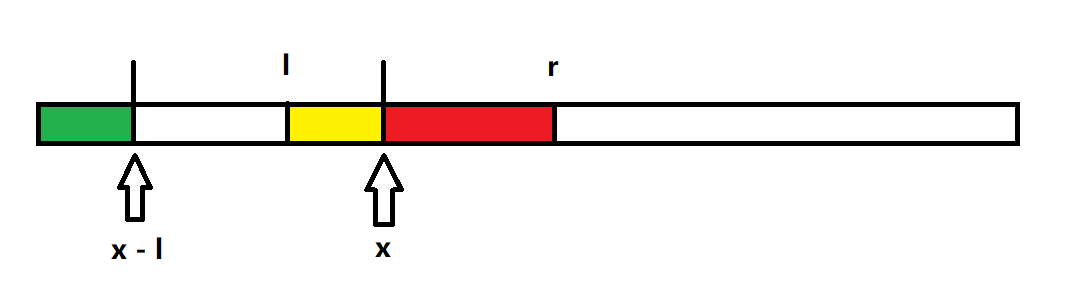
因此,\(z[x]\) 的取值可以參考 \(z[l - x]\)。
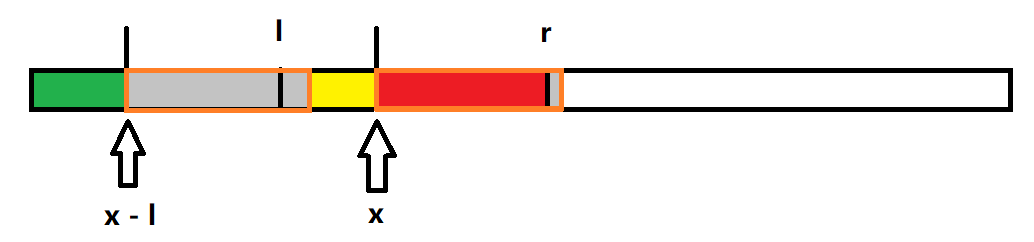
\(z[x]\) 可以直接等於 \(z[l - x]\) 嗎?
顯然是不行的,像下面的情況,灰色區域為 \(z[l - x]\) 的長度,但是,對於 \(x\),有一小段的灰色區域超出了紅色區域,因此不保證這段灰色區域與前面灰色區域的對應位置相等,所以,我們正確的寫法應該是 \(z[x] = \min \{z[l - x], r - x + 1 \}\),隨後再暴力拓展。
-
當 \(x > r\) 時
沒有「前車之鑑」,我們直接進行暴力拓展即可。
程式碼中的 \(i\) 就是 \(x\)。
if (i <= r) {
z[i] = min(z[i - l], 1ll * r - i + 1);
}
暴力拓展 + 修改 \(l, r\)
注意要判斷邊界,同時判斷 \(x + z[x] - 1\) 與 \(r\) 的大小更新 \(l, r\),相信你可以看懂這段程式碼。
while (i + z[i] < len and s[z[i]] == s[i + z[i]]) {
++ z[i];
}
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
拼湊一下,就是 Z 函數(或者是擴充套件 KMP)的程式碼了。
void Z(char* s, ll* z) {
int len = strlen(s), l = 0, r = 0;
rep (i, 1, len - 1, 1) {
if (i <= r) {
z[i] = min(z[i - l], 1ll * r - i + 1);
}
while (i + z[i] < len and s[z[i]] == s[i + z[i]]) {
++ z[i];
}
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
}
}
匹配所有子串
為了避免混淆,我們將 \(t\) 稱作 文字,將 \(p\) 稱作 模式。所給出的問題是:尋找在文字 \(t\) 中模式 \(p\) 的所有出現。
為了解決該問題,我們構造一個新的字串 \(s = p + \diamond + t\),也即我們將 \(p\) 和 \(t\) 連線在一起,但是在中間放置了一個分割字元 \(\diamond\)(我們將如此選取 \(\diamond\) 使得其必定不出現在 \(p\) 和 \(t\) 中)。
首先計算 \(s\) 的 Z 函數。接下來,對於在區間 \([0,\left |t \right | - 1]\) 中的任意 \(i\),我們考慮以 \(t[i]\) 為開頭的字尾在 \(s\) 中的 Z 函數值 \(k = z[i + \left |p \right | + 1]\)。如果 \(k = \left |p \right |\),那麼我們知道有一個 \(p\) 的出現位於 \(t\) 的第 \(i\) 個位置,否則沒有 \(p\) 的出現位於 \(t\) 的第 \(i\) 個位置。
其時間複雜度(同時也是其空間複雜度)為 \(O(\left |t \right | + \left |p \right |)\)。
// 匹配 A 在 B 中的所有出現
void Z(char* s, ll* z) {
int len = strlen(s), l = 0, r = 0;
rep (i, 1, len - 1, 1) {
if (i <= r) {
z[i] = min(z[i - l], 1ll * r - i + 1);
}
while (i + z[i] < len and s[z[i]] == s[i + z[i]]) {
++ z[i];
}
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
}
}
void get_ext() {
strcpy(p, b);
strcat(p, "#");
strcat(p, a);
Z(p, z);
}
P5410 【模板】擴充套件 KMP(Z 函數) - 洛谷 | 電腦科學教育新生態 (luogu.com.cn)
//The code was written by yifan, and yifan is neutral!!!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 2e7 + 5;
ll z[N << 1];
char a[N], b[N], p[N << 1];
void input() {
scanf("%s", a);
scanf("%s", b);
}
void Z(char* s, ll* z) {
int len = strlen(s), l = 0, r = 0;
rep (i, 1, len - 1, 1) {
if (i <= r) {
z[i] = min(z[i - l], 1ll * r - i + 1);
}
while (i + z[i] < len and s[z[i]] == s[i + z[i]]) {
++ z[i];
}
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
}
}
void get_ext() {
strcpy(p, b);
strcat(p, "#");
strcat(p, a);
Z(p, z);
}
void solve() {
int lenz = strlen(b);
int lenext = strlen(p);
ll ans = 0;
z[0] = lenz;
rep (i, 0, lenz - 1, 1) {
ans = ans ^ ((i + 1) * (z[i] + 1));
}
cout << ans;
putchar('\n');
ans = 0;
rep (i, lenz + 1, lenext - 1, 1) {
ans = ans ^ ((i - lenz) * (z[i] + 1));
}
cout << ans;
putchar('\n');
}
int main() {
input();
get_ext();
solve();
return 0;
}
字串整週期
給定一個長度為 \(n\) 的字串 \(s\),找到其最短的整週期,即尋找一個最短的字串 \(t\),使得 \(s\) 可以被若干個 \(t\) 拼接而成的字串表示。
考慮計算 \(s\) 的 Z 函數,則其整週期的長度為最小的 \(n\) 的因數 \(i\),滿足 \(i+z[i]=n\)。
題目
P7114 [NOIP2020] 字串匹配 - 洛谷 | 電腦科學教育新生態 (luogu.com.cn)
求出每個位置的 Z 函數,通過判斷 \((AB)\) 個數的奇偶來計算出現奇數次字元的個數,用樹狀陣列維護。
//The code was written by yifan, and yifan is neutral!!!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))
#define lowbit(x) (x & (-x))
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 2e6 + 5;
int T, n, all, prefix, suffix;
int pre[30], nxt[30], Z[N], t[30];
char s[N];
void input() {
scanf("%s", s);
}
void exkmp() {
int l = 0, r = 0;
rep (i, 1, n - 1, 1) {
if (i <= r) {
Z[i] = min(Z[i - l], r - i + 1);
}
while (s[i + Z[i]] == s[Z[i]] and i + Z[i] < n) {
++ Z[i];
}
if (i + Z[i] - 1 > r) {
r = i + Z[i] - 1;
l = i;
}
}
Z[0] = n;
}
void modify(int x) {
while (x <= 27) {
++ t[x];
x += lowbit(x);
}
}
int query(int x) {
int ans = 0;
while (x) {
ans += t[x];
x -= lowbit(x);
}
return ans;
}
void deal() {
n = strlen(s);
memset(pre, 0, sizeof pre);
memset(nxt, 0, sizeof nxt);
memset(Z, 0, sizeof Z);
memset(t, 0, sizeof t);
all = prefix = suffix = 0;
exkmp();
rep (i, 0, n - 1, 1) {
if (i + Z[i] == n) {
-- Z[i];
}
}
rep (i, 0, n - 1, 1) {
++ nxt[s[i] - 'a'];
}
rep (i, 0, 25, 1) {
if (nxt[i] & 1) {
++ all;
}
}
suffix = all;
ll ans = 0;
rep (i, 0, n - 1, 1) {
if (nxt[s[i] - 'a'] & 1) {
-- suffix;
} else {
++ suffix;
}
-- nxt[s[i] - 'a'];
if (pre[s[i] - 'a'] & 1) {
-- prefix;
} else {
++ prefix;
}
++ pre[s[i] - 'a'];
if (i != 0 && i != n - 1) {
int t = Z[i + 1] / (i + 1) + 1;
ans += 1ll * (t / 2) * query(all + 1) + 1ll * (t - t / 2) * query(suffix + 1);
}
modify(prefix + 1);
}
cout << ans << '\n';
}
void solve() {
T = read<int>();
while (T --) {
input();
deal();
}
}
int main() {
solve();
return 0;
}