Note：[ wechat：Y466551 | 可加勿騷擾，付費諮詢 ]

論文資訊

論文標題：Black-box Source-free Domain Adaptation via Two-stage Knowledge Distillation
論文作者：Shuai Wang, Daoan Zhang, Zipei Yan, Shitong Shao, Rui Li
論文來源：2023 aRxiv
論文地址：download
論文程式碼：download
視屏講解：click

1 介紹

　　動機：無源域自適應的目標是僅使用預先訓練過的源模型和目標資料來適應深度神經網路。然而，存取源模型仍然存在洩漏源資料的潛在問題。在本文中，研究了一個具有挑戰性但實際的問題：黑盒無源域自適應，其中只有源模型和目標資料的輸出可用；

　　方法簡介：提出了一種簡單而有效的兩階段知識蒸餾方法。在第一階段，用源模型以知識蒸餾的方式對源模型生成的軟偽標籤從頭開始訓練目標模型。在第二階段，初始化另一個模型作為新的學生模型，以避免噪聲偽標記引起的誤差積累；

2 相關

　　SFDA 存在的問題：

• • 可以使用生成模型[10,11]來恢復源資料，可能會引發潛在的資料安全問題；
  • 通常會調整源模型的引數，所以目標模型必須使用和源模型相同的方法網路架構作為模型，這對於低源目標使用者，即一些社群醫院是不現實的；

3 方法

模型框架

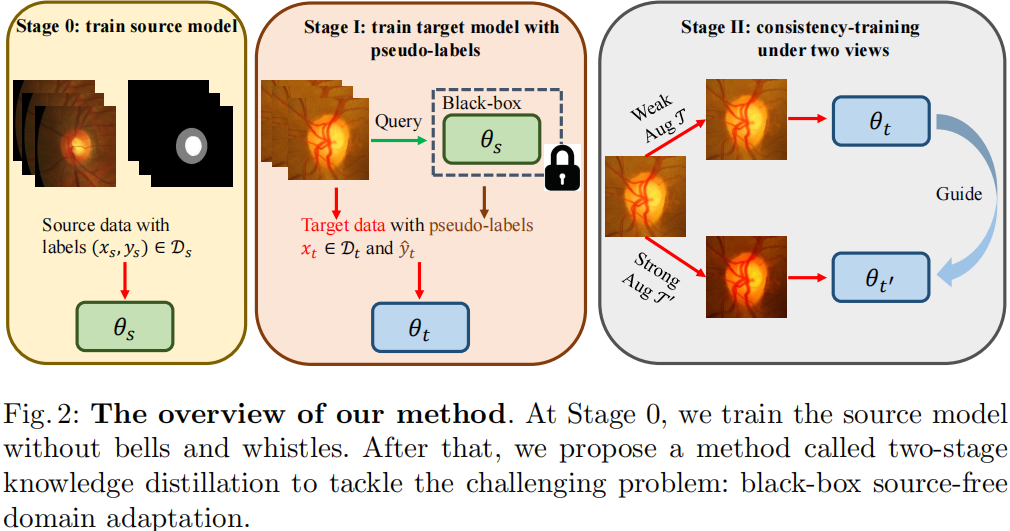
　　對比：

• • UDA：    源資料（√）、源模型（√）
  • SFDA：  源資料（×）、源模型（√）
  • BSFDA：源資料（×）、源模型（×）　　

　　注意：BSFDA 是通過源域資料預訓練好源模型，然後可以通過 API 的形式輸入資料到雲端源模型（Black-box）得到輸出；

3.1 源模型訓練

　　源域資料訓練源模型，交叉熵損失：

　　　　$\mathcal{L}_{s}=-\mathbb{E}_{\left(x_{s}, y_{s}\right) \in \mathcal{D}_{s}} y_{s} \log f_{s}\left(x_{s}\right)$

　　注意：在此之後，就無法存取源模型和源資料，只能利用源模型的輸出；

3.2 兩階段知識蒸餾

　　對於目標域資料 $x_t$，可以使用帶有開放 API 的黑盒源模型 $f_s$ 得到軟偽標籤 $\hat{y}_{t}=f_{s}\left(x_{t}\right)$。

　　訓練目標模型的一個簡單策略是使用具有交叉熵損失的偽標籤 $\hat{y}_{t}$ 的自訓練，但是使用這種偽標籤存在的問題：

• • 由於源域和目標域之間的分佈位移，偽標籤不可避免地成為噪聲；
  • 偽標籤被凍結，因為在源訓練後無法更新源模型；

　　在第一階段，使用軟偽標籤而不是硬標籤從頭開始訓練目標模型 $f_t$ ，目的是從源域獲取更多的幫助知識；

　　在第二階段，另一個模型被隨機初始化，以避免錯誤積累。然後，使用弱資料增強下的偽標籤來指導強增強影象的學習；

第一階段

　　在這個階段，使用知識蒸餾[12]從源模型中精確提取知識：

　　　　$\mathcal{L}_{1}=D_{\mathrm{KL}}\left(\hat{y}_{t} \| f_{t}\left(x_{t}\right)\right)$

　　使用軟標籤的好處：

• • 軟標籤可以提供來自源模型的知識[12]；
  • 對於域外資料，軟偽標籤比硬偽標籤工作得更好；

　　方法具有一定的效果，但模型 $f_t$ 是在有噪聲和固定標籤 $f_t$ 的目標域上進行訓練的，這對目標域是次優的。因此，利用第二階段來增強訓練的模型 $f_t$ 依賴於知識蒸餾之間的兩個影象。

　　使用預訓練模型初始化另外一個模型 $f_{t^{\prime}}$，對目標域資料分別進行 弱、強資料增廣  $\mathcal{T}\left(x_{t}\right)$、$\mathcal{T}^{\prime}\left(x_{t}\right)$。將弱增強影象 $\mathcal{T}\left(x_{t}\right)$ 輸入 $f_{t}$，得到偽標籤 $\hat{y}_{t}^{\prime}=f_{t}\left(\mathcal{T}\left(x_{t}\right)\right)$。之後，使用 $\hat{y}_{t}^{\prime}$ 來指導輸入強增廣資料 $\mathcal{T}^{\prime}\left(x_{t}\right)$ 的模型 $f_{t^{\prime}}$ ，因為弱增廣資料通常會產生更可靠的偽標籤。

　　　　$\mathcal{L}_{2}=D_{\mathrm{KL}}\left(\hat{y}_{t}^{\prime} \| f_{t^{\prime}}\left(\mathcal{T}^{\prime}\left(x_{t}\right)\right)\right)$

　　最後，得到了用於評估的目標模型 $f_{t^{\prime}}$。　

3 實驗

分類結果

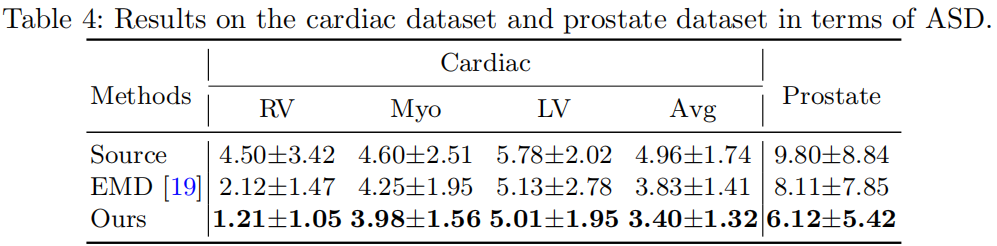
 　　資料集太小了，baseline太少，不做評價；