1. 簡介

1.1 線性迴歸模型概述

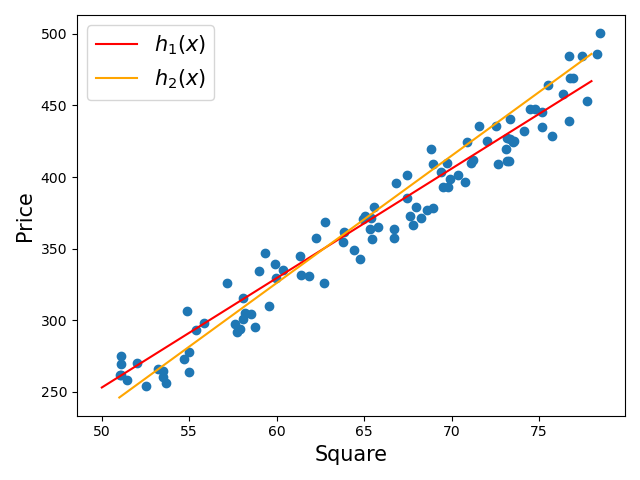
線性迴歸是一種統計學中的預測分析，該方法用於建立兩種或兩種以上變數間的關係模型。線性迴歸使用最佳的擬合直線（也稱為迴歸線）在獨立（輸入）變數和因變數（輸出）之間建立一種直觀的關係。簡單線性迴歸是輸入變數和輸出變數之間的線性關係，而多元線性迴歸是多個輸入變數和輸出變數之間的線性關係。

1.2 Python和PyTorch簡介

Python 是一種強大的程式語言，特別適合處理和分析巨量資料，廣泛應用於各種科學計算中。Python有很多庫可以方便地實現各種高階功能，例如：NumPy, Pandas, Matplotlib等。

PyTorch 是一個開源的 Python 機器學習庫，基於 Torch。它主要由 Facebook 的 AI 研究團隊開發，用於實現深度學習演演算法。PyTorch 以張量為基本資料結構，可以在GPU或CPU上進行計算。具有動態定義計算圖的特性，使得 PyTorch 在編寫和偵錯模型方面更具優勢。

在接下來的部分，我們將使用Python和PyTorch庫實現線性迴歸模型。

2. 工具和庫的準備

在開始實現線性迴歸模型之前，我們需要準備好相關的工具和庫。我們將使用Python作為程式語言，而PyTorch將作為主要的深度學習庫。

2.1 Python環境設定

首先，我們需要安裝Python。如果你的計算機上還沒有安裝Python，可以從Python的官方網站下載：https://www.python.org/downloads/
安裝完成後，可以通過在命令列中執行以下命令來驗證Python是否安裝成功：

python --version

你應該能看到Python的版本號。如果Python已成功安裝，我們可以開始安裝必要的Python庫。這些庫包括：NumPy，Pandas，Matplotlib 和 PyTorch。

2.2 PyTorch安裝與使用簡介

接下來，我們需要安裝PyTorch庫。PyTorch的安裝過程取決於你的作業系統和你是否已經安裝了CUDA（如果你打算在GPU上執行PyTorch，那麼你需要CUDA）。你可以在PyTorch官方網站上找到詳細的安裝指南：https://pytorch.org/get-started/locally/

在命令列中執行以下命令，根據你的環境選擇合適的命令：

# For CPU only
pip install torch==1.9.0+cpu torchvision==0.10.0+cpu torchaudio===0.9.0 -f https://download.pytorch.org/whl/torch_stable.html

# For CUDA 10.2
pip install torch==1.9.0+cu102 torchvision==0.10.0+cu102 torchaudio===0.9.0 -f https://download.pytorch.org/whl/torch_stable.html

安裝完成後，我們可以通過執行以下Python程式碼來驗證PyTorch是否已成功安裝：

import torch
print(torch.__version__)

3. 資料準備

3.1 資料集概述

在這個範例中，我們將使用一個虛構的資料集，該資料集包含房屋面積和價格的資訊。我們的目標是通過面積來預測房價，這是一個典型的線性迴歸問題。

假設我們有以下資料：

面積（平方米）	價格（萬元）
50	300
60	360
70	420
...	...

3.2 資料載入和預處理

接下來，我們需要載入資料並進行預處理。這通常包括缺失值的處理，資料規範化等步驟。在這個範例中，我們假設所有資料都是完整的，不需要進行缺失值處理。但是，為了使梯度下降演演算法能更快地收斂，我們需要對資料進行規範化處理。

import numpy as np

# 房屋面積
areas = np.array([50, 60, 70, ..., 120, 130, 140], dtype=float)

# 房價
prices = np.array([300, 360, 420, ..., 720, 780, 840], dtype=float)

# 資料規範化
areas = (areas - np.mean(areas)) / np.std(areas)
prices = (prices - np.mean(prices)) / np.std(prices)

上面的程式碼首先定義了房屋面積和價格的陣列，然後對這兩個陣列進行了規範化處理，即使得這兩個陣列的值在0附近波動，標準差為1。這樣處理的好處是可以加速梯度下降的收斂。

4. 線性迴歸理論基礎

在這一部分，我們將介紹線性迴歸的基本理論知識，包括線性迴歸的數學模型和梯度下降法。

4.1 線性迴歸模型公式

線性迴歸模型的基本公式如下：

y = wx + b

其中，y是我們要預測的目標變數，x是我們的特徵變數，w和b是我們的模型引數，分別代表權重和偏置。

4.2 損失函數和梯度下降

為了訓練我們的模型，我們需要一個方法來度量我們的模型的預測值和實際值之間的差距。這就是損失函數（也叫成本函數）。對於線性迴歸模型，我們通常使用均方誤差（MSE）作為損失函數：

L = 1/N * ∑(y_pred - y_actual)^2

其中，y_pred是模型的預測值，y_actual是實際值，N是樣本的數量。

我們的目標是通過調整模型的引數w和b來最小化損失函數。這個過程被稱為優化。梯度下降是一種常見的優化方法，工作原理是計算損失函數關於引數的梯度（導數），然後按照梯度的反方向調整引數，以便在損失函數上下降。

5. 使用PyTorch實現線性迴歸模型

有了前面的理論基礎，我們現在可以開始使用PyTorch來實現我們的線性迴歸模型。

5.1 定義模型

首先，我們需要定義我們的模型。在PyTorch中，我們可以通過繼承torch.nn.Module類來定義我們的模型，並實現forward方法來定義前向傳播。

import torch
import torch.nn as nn

class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(1, 1)  # 輸入和輸出的維度都是1

    def forward(self, x):
        out = self.linear(x)
        return out

5.2 範例化模型類

然後，我們可以建立一個模型的範例。

model = LinearRegressionModel()

5.3 設定損失函數和優化器

接下來，我們定義我們的損失函數和優化器。我們使用均方誤差作為損失函數，使用隨機梯度下降作為優化器。

criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

5.4 訓練模型

最後，我們可以開始訓練我們的模型。

# 轉換為 PyTorch 張量
inputs = torch.from_numpy(areas)
targets = torch.from_numpy(prices)

# 轉換為二維張量
inputs = inputs.view(-1,1)
targets = targets.view(-1,1)

# 進行 60 輪訓練
for epoch in range(60):
    # 前向傳播
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    
    # 反向傳播和優化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if (epoch+1) % 5 == 0:
        print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, 60, loss.item()))

上述程式碼將完成線性迴歸模型的訓練過程，訓練結果將在控制檯輸出。

6. 模型評估與預測

訓練完成後，我們需要評估模型的效能，並使用模型進行預測。

6.1 模型評估

首先，我們可以計算模型在所有訓練資料上的平均損失。

model.eval()  # 將模型設定為評估模式
with torch.no_grad():  # 不需要計算梯度
    predictions = model(inputs)
    loss = criterion(predictions, targets)
print('Final Loss:', loss.item())

在這裡，model.eval()是將模型設定為評估模式，這樣在計算梯度時，不會考慮到dropout和batch normalization等操作。torch.no_grad()是告訴PyTorch我們不需要計算梯度，因為我們不需要進行模型優化。

6.2 模型預測

下面我們來使用訓練好的模型進行預測。

# 預測一個 100 平方米的房子的價格
area = torch.tensor([100.0])
area = (area - torch.mean(inputs)) / torch.std(inputs)  # 需要進行同樣的資料規範化
price = model(area)
print('Predicted price:', price.item())

上述程式碼使用訓練好的模型預測了一個100平方米房子的價格。需要注意的是，我們在預測新資料時，需要對新資料進行與訓練資料相同的預處理操作。

到此為止，我們已經完成了線性迴歸模型的全部內容，包括理論知識的學習，使用PyTorch進行模型實現和訓練，以及模型的評估和預測。

7. 總結

我們已經完成了一次完整的線性迴歸模型的構建、訓練和預測過程。在這個過程中，我們學習了線性迴歸模型的基本理論知識，如何使用PyTorch實現線性迴歸模型，以及如何評估和使用訓練好的模型。

7.1 關鍵點總結

在本文中，我們主要做了以下幾點內容：

介紹了線性迴歸模型的基本概念和數學原理。
使用Python和PyTorch實現了線性迴歸模型的訓練和預測過程。
展示瞭如何評估模型的效能。

通過這次的學習，希望你對線性迴歸模型有了更深的理解，並能在實際問題中靈活運用。

7.2 展望

雖然線性迴歸模型是最基本的機器學習模型，但是其思想和方法在許多複雜的模型中都有所體現。例如，神經網路就可以看作是對線性迴歸模型的擴充套件和深化。因此，理解和掌握線性迴歸模型對於學習更復雜的機器學習模型非常重要。

如有幫助，請多關注
個人微信公眾號：【TechLead】分享AI與雲服務研發的全維度知識，談談我作為TechLead對技術的獨特洞察。
TeahLead KrisChang，10+年的網際網路和人工智慧從業經驗，10年+技術和業務團隊管理經驗，同濟軟體工程本科，復旦工程管理碩士，阿里雲認證雲服務資深架構師，上億營收AI產品業務負責人。

Python和PyTorch深入實現線性迴歸模型：一篇文章全面掌握基礎機器學習技術