FPGA移位加三法
介紹
BCD碼
BCD碼的英文全稱是Binary-Coded Decimal,簡稱BCD,按字面解釋是二進位制十進位制程式碼,是一種二進位制的數位編碼形式。
常見的BCD碼有8421BCD碼,2421BCD碼,5421BCD碼,餘3碼以及格雷碼等等。
在本文中,我們所採用的BCD碼為8421BCD碼。
8421碼,即從左到右的二進位制位權重分別為8、4、2、1。即
| BCD碼 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
|---|---|---|---|---|---|---|---|---|---|---|
| 值 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
應用場景
數位時鐘,需要十進位制地顯示時分秒;溫度顯示也需要十進位制;次數顯示也需要十進位制······
錯誤例子
module func(i_data, o_data)
input wire [7:0] i_data;
output wire [11:0] o_data;
assign o_data[11:8] = i_data / 100;
assign o_data[7:4] = i_data / 10 % 10;
assign o_data[3:0] = i_data % 10;
endmodule
這是我們在做演演算法題的時候用到的方法,而且Verilog是支援除法和取餘運算的,但是這樣會耗費太多資源。對於硬體設計來說,我們需要用適合硬體的方法。
8421碼與二進位制碼的關係
對於4位元二進位制碼,是逢16進位。而8421碼是逢10進位。
因此,大於9的二進位制碼,加6就可以得到8421碼。
移位加三法
首先給出步驟:(8位元二進位制數為例)
- BCD碼初始化為0。
- 將原二進位制碼左移一位,左移出的一位添到BCD碼的低位上。
- 判斷BCD碼所對應的個,十,百位是否大於等於5,如果是則該段加3。
- 繼續重複以上步驟直到移位8次後停止。
總之,在移位的過程中,如果移位出的數值大於等於5,則將數值加3,再進行移位。對於n位二進位制數,就進行n次移位。
例子
以二進位制數 0111_1101為例,數值為125。
| 百位 | 十位 | 個位 | 二進位制數 | |
|---|---|---|---|---|
| 開始 | 4'b0000 | 4'b0000 | 4'b0000 | 8'b0111_1101 |
| 左移1 | 4'b0000 | 4'b0000 | 4'b0000 | 8'b1111_1010 |
| 左移2 | 4'b0000 | 4'b0000 | 4'b0001 | 8'b1111_0100 |
| 左移3 | 4'b0000 | 4'b0000 | 4'b0011 | 8'b1110_1000 |
| 左移4 | 4'b0000 | 4'b0000 | 4'b0111 | 8'b1101_0000 |
| 加3 | 4'b0000 | 4'b0000 | 4'b1010 | 8'b1101_0000 |
| 左移5 | 4'b0000 | 4'b0001 | 4'b0101 | 8'b1010_0000 |
| 加3 | 4'b0000 | 4'b0001 | 4'b1000 | 8'b1010_0000 |
| 左移6 | 4'b0000 | 4'b0011 | 4'b0001 | 8'b0100_0000 |
| 左移7 | 4'b0000 | 4'b0110 | 4'b0010 | 8'b1000_0000 |
| 加3 | 4'b0000 | 4'b1001 | 4'b0010 | 8'b1000_0000 |
| 左移8 | 4'b0001 | 4'b0010 | 4'b0101 | 8'b0000_0000 |
可以看到,最終結果為 12'b0001_0010_0101。按照8421BCD碼解析,即為125。
為什麼要大於等於5
之前的聯絡不是說,大於9嘛?其實這只是一個簡單的運算前後順序關係。
BCD碼是4位元二進位制數表示一個十進位制數的1位,如果大於等於5,比如5,4'b0101,下一次移位後變成了4’b1010,而BCD碼中是沒有4’b1010的,所以要加6,向高位進位。(見聯絡)
所以移位後加6和移位前加3都是可以的。
具體實現
實現一
RTL結構
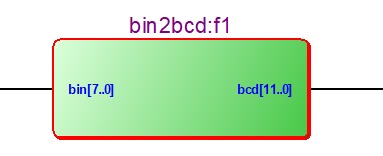
- bin[7:0]:二進位制數輸入
- bcd[11:0]:8421BCD碼輸出,[11:8] 為百位,[7:4] 為十位,[3:0] 為個位。
- 該模組呼叫8次移位加3模組,如圖:


程式碼
移位加3模組
module shift(i_data, o_data);
input wire [19:0] i_data;
output wire [19:0] o_data;
wire [19:0] shift_data;
assign shift_data[19:16] = i_data[19:16] > 4'd4 ? i_data[19:16] + 4'd3 : i_data[19:16];
assign shift_data[15:12] = i_data[15:12] > 4'd4 ? i_data[15:12] + 4'd3 : i_data[15:12];
assign shift_data[11:8] = i_data[11:8] > 4'd4 ? i_data[11:8] + 4'd3 : i_data[11:8];
assign shift_data[7:0] = i_data[7:0];
assign o_data = shift_data << 1'b1;
endmodule
頂層模組
module bin2bcd(bin, bcd);
input wire [7:0] bin;
output wire [11:0] bcd;
wire [19:0] w_0;
wire [19:0] w_1;
wire [19:0] w_2;
wire [19:0] w_3;
wire [19:0] w_4;
wire [19:0] w_5;
wire [19:0] w_6;
wire [19:0] w_7;
shift shift_ins0 (.i_data({12'd0, bin}), .o_data(w_0));
shift shift_ins1 (.i_data(w_0), .o_data(w_1));
shift shift_ins2 (.i_data(w_1), .o_data(w_2));
shift shift_ins3 (.i_data(w_2), .o_data(w_3));
shift shift_ins4 (.i_data(w_3), .o_data(w_4));
shift shift_ins5 (.i_data(w_4), .o_data(w_5));
shift shift_ins6 (.i_data(w_5), .o_data(w_6));
shift shift_ins7 (.i_data(w_6), .o_data(w_7));
assign bcd = w_7[19:8];
endmodule
實現二
- inData[15:0]:二進位制數輸入
- outData[19:0]:8421BCD碼輸出,個十百千位同理。
- 本程式碼通過迴圈實現。
程式碼
module BinaryToBCD(
input wire [16-1:0] inData, //二進位制輸入
output wire [16+3:0] outData //BCD輸出
);
parameter bit_binary = 16; //二進位制資料位數
reg [bit_binary-1:0] bin;
reg [bit_binary+3:0] ShiftReg;
always@(inData)
begin
bin = inData;
ShiftReg = 'd0;
repeat (bit_binary - 1)
begin
ShiftReg[0] = bin[bit_binary-1];
//adjust by add 3
if(ShiftReg[19:16] > 4)
ShiftReg[19:16] = ShiftReg[19:16] + 2'd3;
else
ShiftReg[19:16] = ShiftReg[19:16];
if(ShiftReg[15:12] > 4)
ShiftReg[15:12] = ShiftReg[15:12] + 2'd3;
else
ShiftReg[15:12] = ShiftReg[15:12];
if(ShiftReg[11:8] > 4)
ShiftReg[11:8] = ShiftReg[11:8] + 2'd3;
else
ShiftReg[11:8] = ShiftReg[11:8];
if(ShiftReg[7:4] > 4)
ShiftReg[7:4] = ShiftReg[7:4] + 2'd3;
else
ShiftReg[7:4] = ShiftReg[7:4];
if(ShiftReg[3:0] > 4)
ShiftReg[3:0] = ShiftReg[3:0] + 2'd3;
else
ShiftReg[3:0] = ShiftReg[3:0];
ShiftReg = ShiftReg << 1;
bin = bin << 1;
end
ShiftReg[0] = bin[bit_binary-1];
end
assign outData = ShiftReg;
endmodule
參考文獻
[1] https://blog.51cto.com/u_15076212/3816404 "基於FPGA的二進位制轉BCD設計與實現(移位加3法)"
[2] https://zhuanlan.zhihu.com/p/209083141 "[走近FPGA]之二進位制轉BCD碼"
本文來自部落格園,作者:江水為竭,轉載請註明原文連結:https://www.cnblogs.com/Az1r/p/17584630.html