量子力學的應用：量子計算

親愛的讀者，

歡迎回到我們的量子力學系列文章。在前面的幾篇文章中，我們已經深入探討了量子力學的起源、基本概念、實驗驗證以及解釋問題。今天，我們將聚焦在量子力學的一個引人注目的應用領域：量子計算。

1. 傳統計算機與量子計算機的區別

在傳統計算機中，資訊由位元表示，每個位元的狀態可以是0或1。而在量子計算機中，資訊由量子位元（或稱為量子位或qubit）表示，它們可以處於0和1的疊加態。這個特性使得量子計算機具有處理大規模平行計算的潛力，從而在某些特定問題上能夠遠遠超越傳統計算機。

量子計算機的計算模型採用量子位的疊加和糾纏來進行計算。量子糾纏是一種奇特的量子現象，當兩個或多個量子位糾纏在一起時，它們的狀態是相互關聯的。這種相互關聯的性質使得量子計算機能夠進行平行計算，從而在一些特定的問題上實現指數級的加速。

2. 量子計算的演演算法

量子計算中最著名的演演算法之一是Shor演演算法，它被設計用於分解大整數。在傳統計算機上，對大整數進行質因數分解是非常耗時的，這種問題在密碼學中有著重要的應用。Shor演演算法通過利用量子糾纏和疊加的特性，在多項式時間內解決了這個問題，從而破解了RSA加密等傳統加密方法。

另一個重要的量子演演算法是Grover演演算法，它用於搜尋未排序資料庫中的目標項。在傳統計算機上，搜尋未排序資料庫的時間複雜度是O(N)，其中N是資料庫中項的數量。然而，Grover演演算法可以在O(√N)的時間內找到目標項，從而實現了量子計算的加速效果。

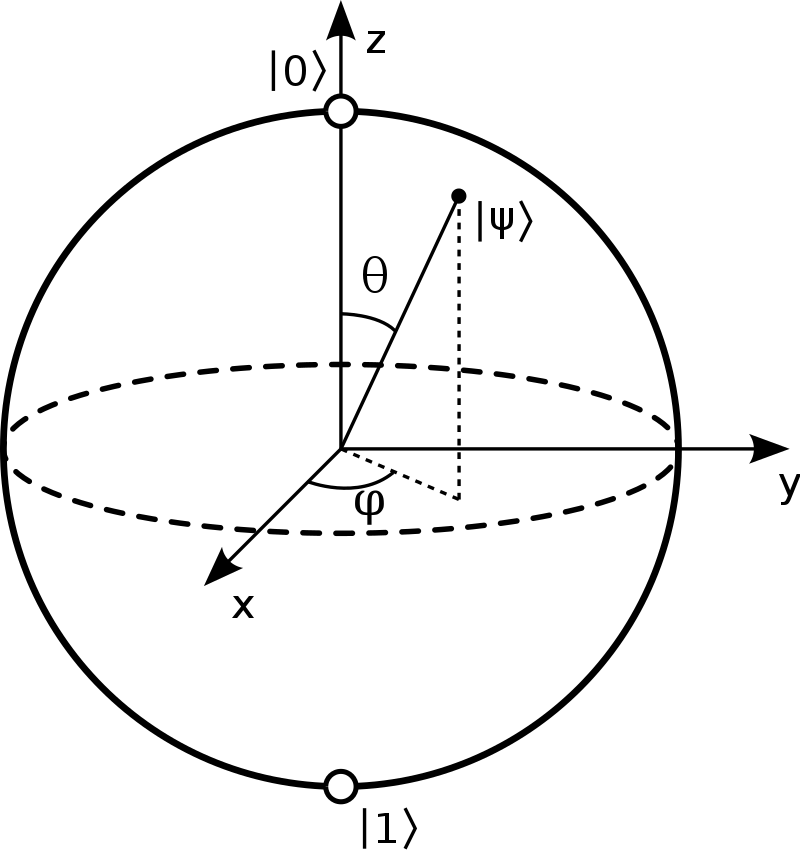
3. 量子位元的表示

在量子計算中，我們使用數學上的復向量空間來表示量子位。一個量子位可以寫成如下形式：

|Ψ⟩ = α|0⟩ + β|1⟩

其中，|0⟩和|1⟩分別表示量子位的基態，α和β是複數係數，表示量子位處於0態和1態的概率振幅。

為了保證量子位的概率振幅滿足歸一化條件，即概率之和為1，我們有：

|α|^2 + |β|^2 = 1

4. 疊加和量子干擾

在量子力學中，疊加是指一個量子系統處於多個狀態的疊加態。例如，一個量子位可以同時處於0態和1態的疊加態，用波函數表示為：

|Ψ⟩ = α|0⟩ + β|1⟩

其中，α和β是複數係數，表示量子位分別處於0態和1態的概率振幅。在疊加態中，量子位處於0態和1態的概率是同時存在的，而不是確定性地處於其中一個狀態。

疊加態的一個重要性質是量子干擾。當兩個或多個量子系統處於疊加態時，它們的量子性質會相互干涉，導致一些奇特的現象。量子干擾是量子計算的重要基礎之一，它使得量子計算在某些問題上能夠實現指數級的加速。

5. 量子門操作

在量子計算中，我們使用量子門操作來進行量子位的操作和控制。量子門操作是一種么正操作，它可以在量子位上進行線性變換，實現量子位之間的糾纏和疊加。

一個常見的量子門操作是Hadamard門，它可以將一個量子位從0態變換到一個等概率的疊加態。Hadamard門的矩陣表示如下：

H = 1/√2 * |0⟩⟨0| + 1/√2 * |0⟩⟨1| + 1/√2 * |1⟩⟨0| - 1/√2 * |1⟩⟨1|

當一個量子位經過Hadamard門操作後，它的狀態將變為：

H|0⟩ = 1/√2 * (|0⟩ + |1⟩)

這是一個等概率的疊加態，記為|+⟩。

6. 量子糾纏的應用

量子糾纏是量子計算中最重要的資源之一。它可以用於實現量子位元之間的相互作用和通訊，從而在量子計算中進行並行運算。

一個著名的量子糾纏應用是量子電報。假設有兩個糾纏的量子位A和B，它們之間的狀態可以表示為：

|Ψ⟩ = 1/√2 * (|00⟩ + |11⟩)

當我們對A進行測量時，B的狀態會瞬間發生改變，即使它們之間的距離非常遠。這種現象被稱為量子糾纏的非局域性，它在量子通訊和量子金鑰分發等領域有著重要的應用。

7. 退相干與量子計算的挑戰

退相干是指量子系統在與外部環境的相互作用下，失去了疊加態的特性，變得更加經典化的過程。當量子系統與外界發生相互作用時，干涉項會被抵消，導致量子疊加態變為經典概率分佈。

退相干是量子資訊的主要敵人之一。在量子計算和量子通訊中，保持量子態的相干性對於實現正確的計算和通訊至關重要。因此，控制和抑制退相干是量子技術研究的一個重要課題。

儘管量子計算在理論上具有巨大的潛力，但要實現大規模的量子計算仍然面臨著許多挑戰。量子位元的相干性和糾纏性非常脆弱，容易受到環境干擾而失去量子性質。

此外，量子計算中的量子位數目和計算複雜性也受到限制。目前，我們只能實現少量的量子位元，遠遠不能滿足大規模量子計算的需求。

8. 公司如何使用量子計算？

量子計算可以顛覆許多行業。我們在下面給出了一些使用場景範例：

• 8.1 ML

機器學習（ML）是分析大量資料以幫助計算機做出更好的預測和決策的過程。量子計算研究研究了資訊處理的物理極限，並在基礎物理學領域開闢了新天地。這項研究促進了多個科學和工業領域（例如化學、優化和分子模擬）的進步。它也是一個日益受關注的領域，金融服務業可以通過它來預測市場動向，製造業也可以通過它來改善運營。

• 8.2 優化

量子計算可以改善研發、供應鏈優化和生產。例如，您可以通過優化複雜流程中的路徑規劃等元素，應用量子計算來降低製造流程相關成本並縮短週期時間。另一個應用是貸款組合的量子優化，以便貸方可以釋放資本、降低利率並改進其產品。

• 8.3 模擬

精確模擬系統所需的計算量隨著藥物分子和材料的複雜性呈指數增長。即使使用近似方法，當前的超級計算機也無法達到這些模擬所需的精度水平。量子計算有可能解決化學中面臨的一些極具挑戰性的計算問題，使科學界能夠進行當今難以處理的化學模擬。例如，Pasqal 構建了他們的 QUBEC 計算軟體來執行化學模擬。QUBEC 將執行量子計算任務所需的繁重工作自動化，涵蓋計算基礎設施的自動設定、執行預處理和後處理經典計算以及執行錯誤緩解任務等。

9. 量子計算的未來展望

儘管面臨挑戰，量子計算依然被認為是未來計算領域的一顆明星。隨著量子技術的不斷髮展，我們相信量子計算會為人類帶來深遠的影響。

在未來，我們有望實現更多量子位元的糾纏和控制，從而實現更復雜的量子計算任務。量子計算將在化學模擬、優化問題、密碼學和人工智慧等領域發揮重要作用，為解決一些傳統計算機難以解決的問題提供新的途徑。

總結

量子計算作為量子力學的一個重要應用領域，提供了一種全新的計算模型和計算正規化。量子計算通過利用量子糾纏和疊加的特性，能夠在一些特定問題上實現指數級的加速效果，遠遠超越傳統計算機的能力。

雖然量子計算仍面臨諸多挑戰，但我們對未來的展望充滿信心。隨著量子技術的不斷進步，我們相信量子計算將為人類帶來前所未有的計算能力和科學發現。