二元堆積

二元堆積具有兩個性質, 結構性和排序性.

結構性質

堆是一棵被完全填滿的二元樹, 叫做完全二元樹, 除了底層以外都被填滿了, 而最底層從左到右填入了.

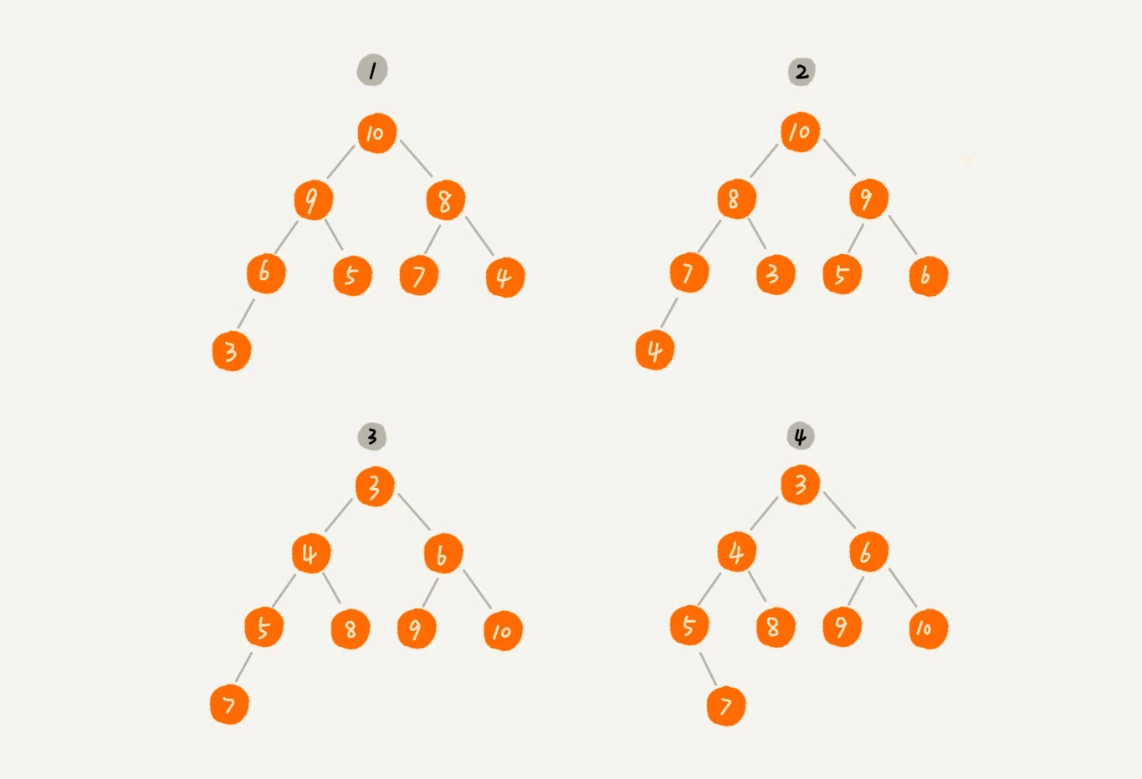
以上圖為例, 1是小頂堆, 2是大頂堆, 3是小頂堆, 4不是堆.
這種完全二元樹並不一定被填滿, 為什麼要被稱作是完全二元樹呢? 這是因為這種二元樹可以被高效的儲存在陣列中. 二元樹通常有兩種方式儲存:

基於連結串列

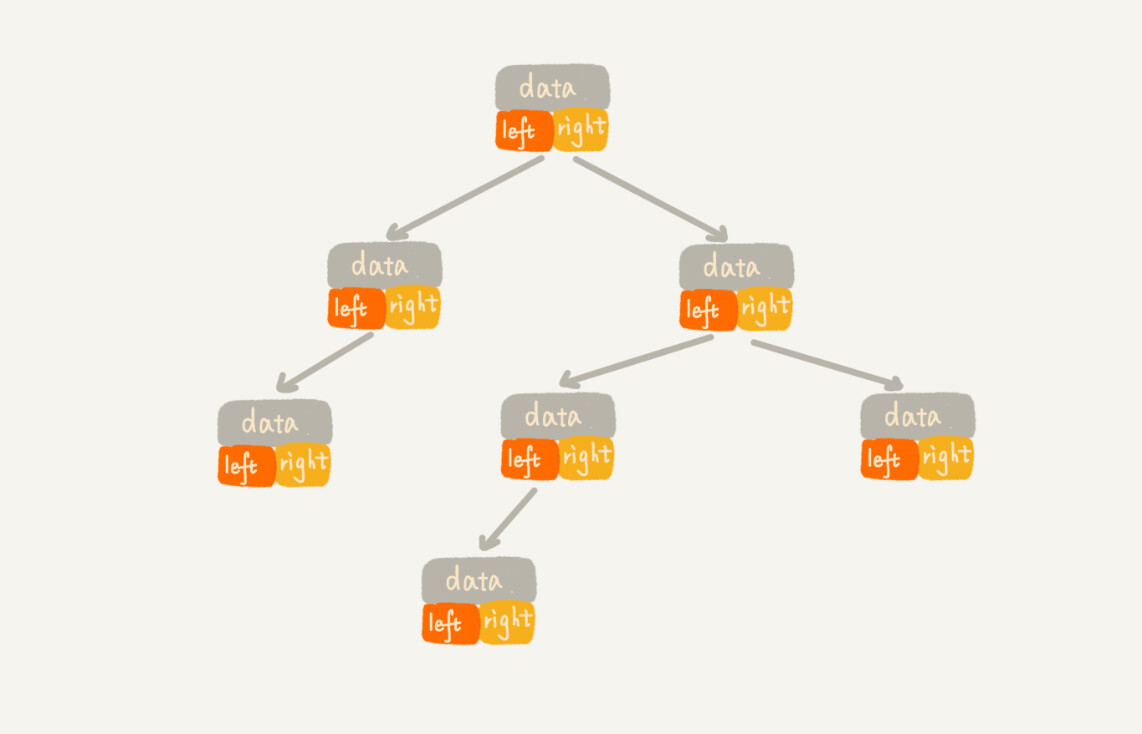
每個節點儲存3個欄位

基於陣列

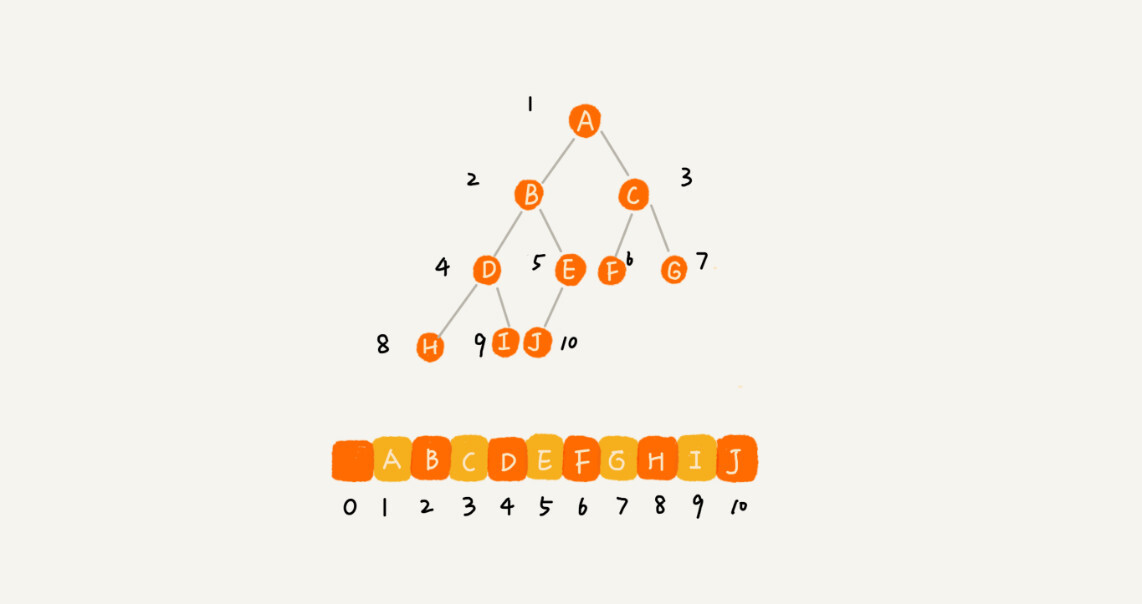
這種方式中根節點儲存在1位, 後面左節點儲存在 2i位, 右子節點儲存在2i+1位. 通過這種方式只要知道根節點的位置, 就可以利用上述的關係構建出整個樹, 這樣的儲存非常的緊密, 不需要額外儲存左右指標.
但是如果二元樹不是滿二元樹按照這種方式儲存就會存在空洞, 造成空間浪費

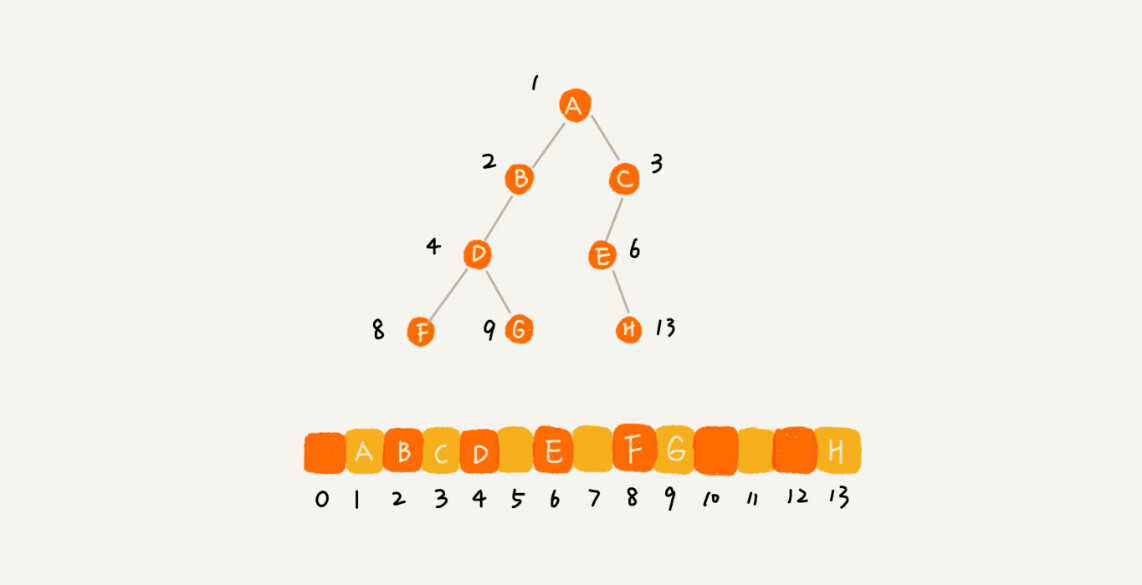
回到堆的話題, 因為堆滿足完全二元樹的結構性, 所以通常堆都是儲存在陣列中.

堆序性質

在一個堆(小根堆)中, 對於每一個節點X, X的父親節點 <= X節點

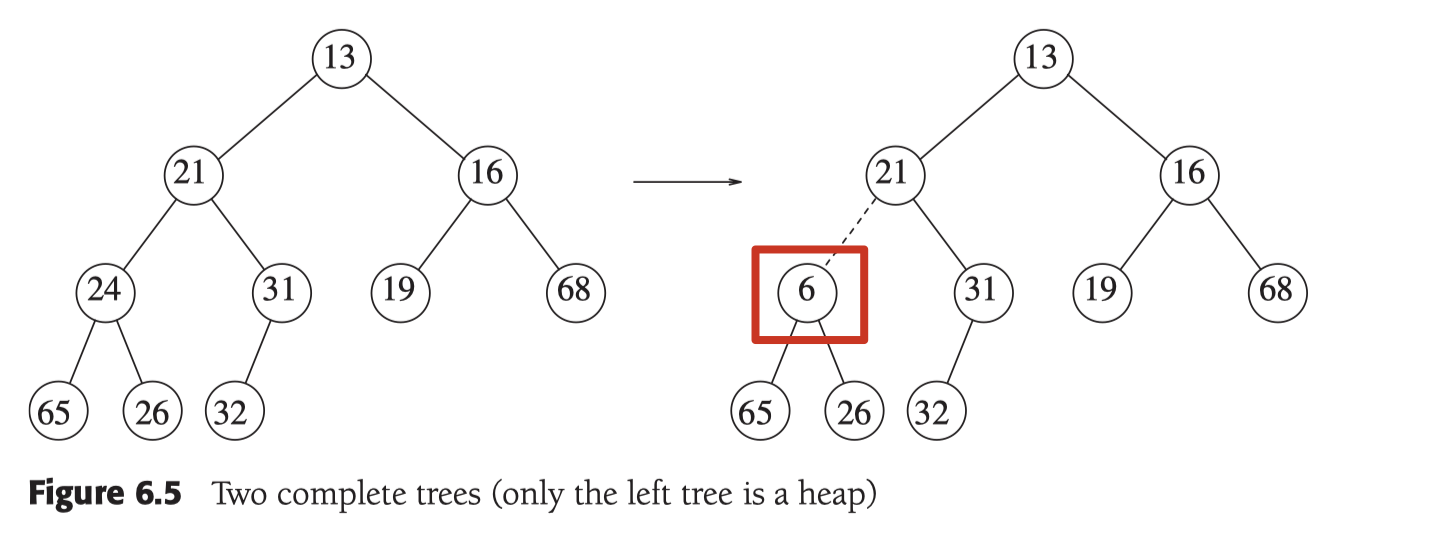
如上圖右側的完全二元樹就不是堆.

從上面定義的資訊可以看出堆所提供的有序性是有限的, 只能知道堆頂是最大或最小值, 因此堆最常用的就是用作優先順序佇列, 優先順序佇列所需要的介面.

add
findMin
deleteMin

在新增和刪除的時候都需要去維護上面提到的兩個堆的性質.

實現

add

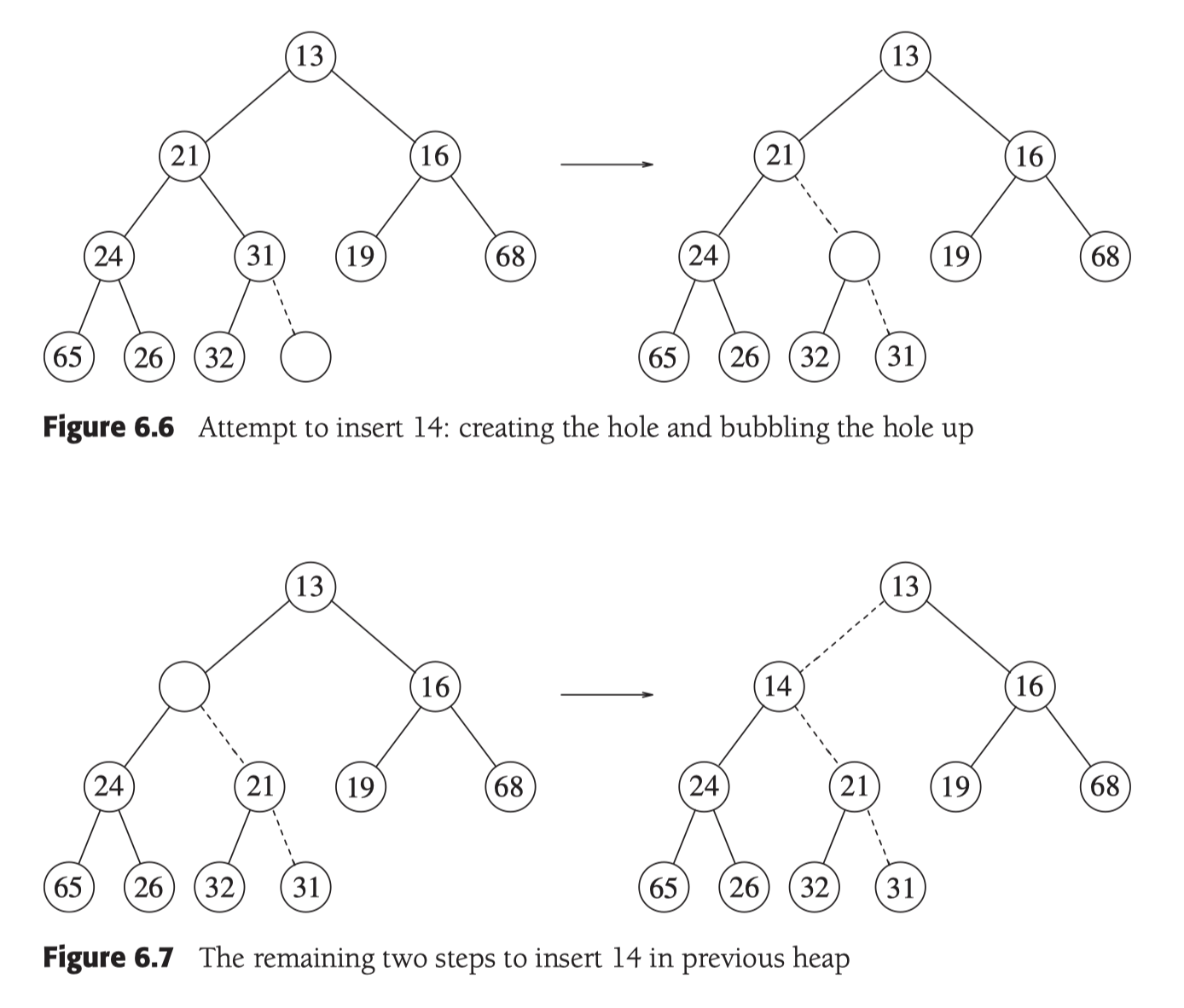
新插入的值預設插在末尾, 這會破快堆的有序性, 所以需要找到合適的位置放置新加入的值. 將插入的值逐步和parent比較, 如果小於parent 則上浮

樣例實現

public void add(int x) {
    if (size == elements.length - 1) {
    enlargeArray();
}

// 複製elements[0]的好處是for迴圈不需要對 index 0 特殊處理
// i = 1時, 就會和elements[0] 作比較
elements[0] = x;
// percolate up / sift up
// i 要從 ++size算起, 不然找的parent可能是錯的
for (int i = ++size; i >= 1; i = i / 2) {
    // 插入值小於父節點, 將父節點下移, 空穴上移
    if (x < elements[i / 2]) {
        elements[i] = elements[i / 2];
    } else {
        elements[i] = x;
        break;
    }
}
}

deleteMin

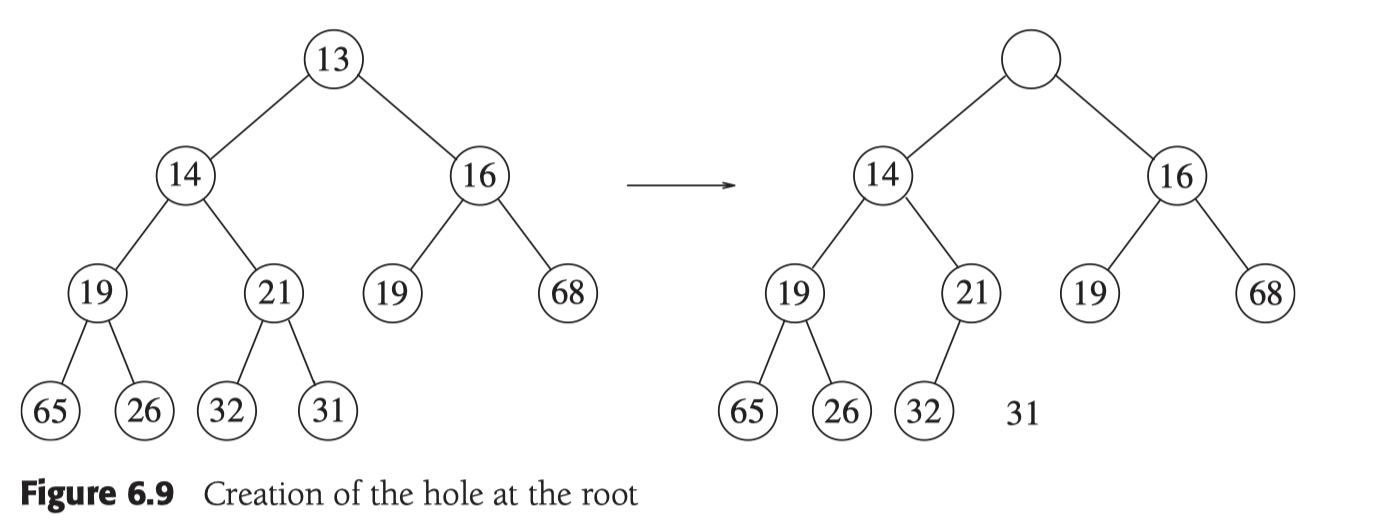
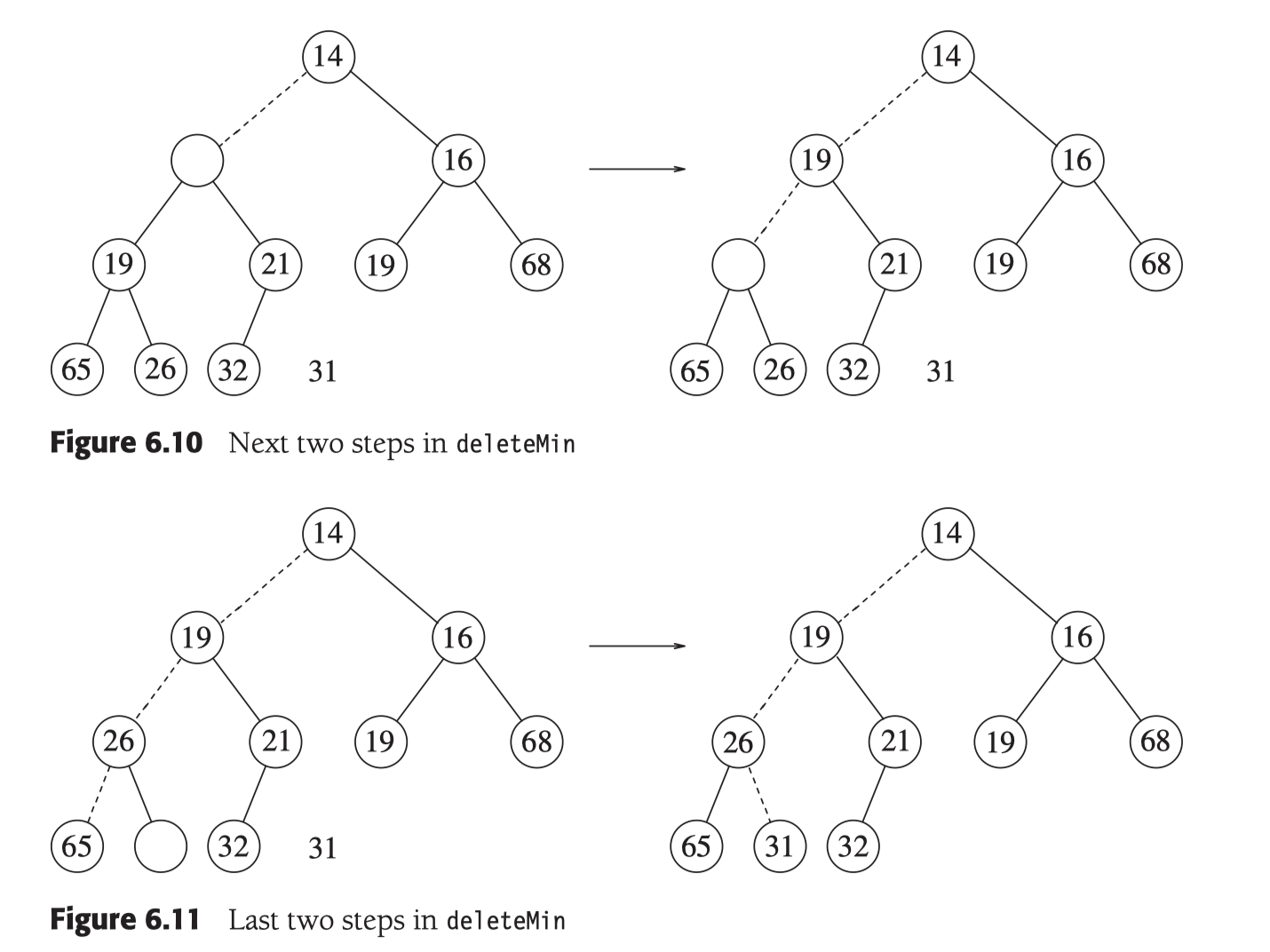
刪除最小值後, 根節點就變成了空值, 為了保障堆的結構性, 將最後一位填充到根節點處, 同時這不一定滿足堆序性質, 所以要和左右子樹逐步比較下沉.

這裡我開始思考的是另一種思路實現

判斷是否右子樹為空或者左子樹小於右子樹, 如果是則左子樹上移, 否則右子樹上移
退出條件為移動到沒有子樹的節點即 i > size /2
退出後將最後一位賦值給當前值

需要注意的是左右子樹不一定都存在

private void deleteMin() {
    int i = 1;
    if (size == 1) {
        size = 0;
        return;
    }
    for (; i <= size / 2;) {
        // 右子樹為空或者左子樹小於右子樹
        if (2 * i + 1 > size || elements[2 * i] < elements[2 * i + 1]) {
            // 左子樹上移
            elements[i] = elements[2 * i];
            i = 2 * i;
        } else {
            elements[i] = elements[2 * i + 1];
            i = 2 * i + 1;
        }
    }

    elements[i] = elements[size];
    size--;
}

書上的解法

首先將last element賦值給array[1]
將array[1] 下沉

這兩種實現差別

第一種的思路是不斷的在兩個子樹中查詢較小值提升
第二種思路是將末尾設定為root後, 不斷地將這個值下沉, 第二種更符合演演算法的 percolate down的描述. 而且第一種一定會比較logN次, 而第二種實際上是可能會提前終止的. 所以第二種的最優執行情況中的比較次數會更少

列印

同樣新增了一個方法來列印堆的結構方便檢驗準確性

private void print() {
    int currentLevel = 0;
    int currentIndent = 0;
    int totalLevel = (int) Math.floor(Math.log(size) / Math.log(2)) + 1;
    StringBuilder levelBuilder = new StringBuilder();
    levelBuilder.append(String.format("level% 2d: ", currentLevel));
    for (int i = 1; i <= size; i++) {
        // 不精確的計算 log2(N)
        int level = (int) Math.floor(Math.log(i) / Math.log(2));
        if (level != currentLevel) {
            System.out.println(levelBuilder.toString());
            currentLevel = level;
            currentIndent = 0;
            levelBuilder = new StringBuilder();
            levelBuilder.append(String.format("level% 2d: ", currentLevel));
        }
        int toLeftIntent = indent(i, totalLevel - 1);
        levelBuilder.append(blank((toLeftIntent - currentIndent), currentLevel));
        currentIndent = toLeftIntent;
        levelBuilder.append(String.format("%d", elements[i]));
    }
    System.out.println(levelBuilder.toString());

    //        for (int i = 1; i <= size; i++) {
    //            System.out.printf("%d ", elements[i]);
    //        }
}

參考

<資料結構與演演算法分析 Java描述> 6.3 BinaryHeap
完全二元樹看起來並不完全，為什麼叫完全二元樹呢？
https://blog.csdn.net/qq_42006733/article/details/104580717

二元堆積原理與實現

二元堆積

結構性質

堆序性質

實現

add

deleteMin

列印

參考