Knowledge Distill

蒸餾思想

知識蒸餾是一種模型壓縮方法，通過引導輕量化的學生模型「模仿」效能更好、結構更復雜的的教學模型（教師模型），在不改變學生模型結構的情況下提高其效能。最早由Hinton在2015年提出，應用於分類任務。知識蒸餾的目的是將教師模型中的知識轉移到學生模型中，從而提高學生模型的效能。這個過程類似於資料壓縮，將重要的資訊從複雜的的資料中提取出來，以便更好地傳輸和儲存。在深度學習中，知識蒸餾通常用於訓練輕量級模型，以獲得與更復雜的模型相似的效能。

知識蒸餾就是將已經訓練好的模型包含的知識，蒸餾到另一個模型中去。具體來說，知識蒸餾，可以將一個網路的知識轉移到另一個網路，兩個網路可以是同構或者異構。一般是將一個複雜模型（或整合模型）蒸餾到一個輕量級模型中以提升執行速度，但也有以提升指標為目的的蒸餾。

蒸餾的常規做法是先訓練一個 teacher 網路，然後使用這個 teacher 網路的輸出和資料的真實標籤去訓練 student 網路。

在訓練過程中，我們需要使用複雜的模型，大量的計算資源，以便從非常大、高度冗餘的資料集中提取出資訊。在實驗中，效果最好的模型往往規模很大，甚至由多個模型整合得到。而大模型不方便部署到服務中去，常見的瓶頸如下:

推斷速度慢
對部署資源要求高(記憶體，視訊記憶體等)，在部署時，我們對延遲以及計算資源都有著嚴格的限制。

因此，模型壓縮(在保證效能的前提下減少模型的引數量)成為了一個重要的問題，而」模型蒸餾「屬於模型壓縮的一種方法。從模型壓縮的角度來看，知識蒸餾像一種正則化的方法，student學習的是teacher的泛化能力，而非過擬合能力。

發展起源

KDD2006論文 Model Compression 中，Rich Caruana 等人提出大型整合模型所獲得的知識可以轉移到單個小型的模型中，屬於蒸餾思想的先驅性的論文。

Geoffrey Hinton 等人在論文 Distilling the Knowledge in a Neural Network（NIPS 2014）中提出了可應用於神經網路模型的知識蒸餾技術。

方法分類

按照待遷移的知識型別，KD主要分為三個大類：

Output Transfer——將網路的輸出（Soft-target）作為知識，常用 Logit Distillation
Feature Transfer——將網路學習的特徵作為知識（特徵蒸餾方法如TinyBERT等）
Relation Transfer——將網路或者樣本的關係作為知識

本文主要介紹前兩個主流技術：Logits方法及特徵蒸餾方法。

BERT 蒸餾

BERT蒸餾方式包括Logit Distillation、特徵蒸餾，其它還有 Curriculum Distillation、Dynamic Early Exit: FastBert 等。

從teacher/student模型結構的相似程度來看，可分成兩種：

第一種，異構，如從 transformer 到非 transformer 框架的知識蒸餾。

這種由於中間層引數的不可比性，導致從 teacher model 可學習的知識比較受限。但比較自由，可以把知識蒸餾到一個非常小的 model，但效果可能會差一些。

第二種，同構，如從 transformer 到 transformer 框架的知識蒸餾。還可細分為中間層同維度/不同維度。

由於中間層引數可利用，所以知識蒸餾的效果會好很多，甚至能夠接近原始 bert 的效果。但 transformer 即使只有三層，引數量其實也不少，另外蒸餾過程的計算也無法忽視。

在業務中選用哪種蒸餾方法，還是要根據真實需求來取捨。

蒸餾方法

Logits蒸餾方法

一般的分類問題最終是通過softmax對logits進行歸一化，在計算交叉熵損失時只有正類對應的logit參與損失的貢獻，而負類標籤被統一對待，但是負類標籤對應的概率存在差異較大的情況，這些資訊被忽略了。Logits蒸餾方法讓student模型的logits（soft target）輸出逼近teacher模型的logits以達到近似softmax預測hard target的目的，如最小化MSE： \(L_{student}={1\over 2}\|z_t-z_s\|^2\)。

在這裡，Teacher的Logits就是傳給Student的暗知識（Dark Knowledge）。

舉一個容易理解的例子，MNIST手寫數位識別任務中包含0~9的數點陣圖片，通過CNN網路接softmax輸出10個類別的概率。比如對於數位2，手寫的形狀有的像3，有的像7，那麼不同的數位2的圖片應當有不同的類別概率分佈。因此如果只用hard target label去訓練，會忽略掉這些細節資訊。

既然Softmax抹除了不同負類之間的差異, 那麼也可以對Softmax進行改造來弱化兩極分化，保留更多的隱含知識。

Hinton在論文Distilling the Knowledge in a Neural Network中提出了稱為Softmax Temperature的改進方法，繼續採用交叉熵損失而非MSE，並第一次正式提出了「知識蒸餾」的叫法。Softmax Temperature改造了Softmax函數，加入溫度係數：

\[q_{i}=\frac{\exp \left(z_{i}\right)}{\sum_{j} \exp \left(z_{j}\right)} \quad \rightarrow \quad q_{i}=\frac{\exp \left(z_{i} / T\right)}{\sum_{j} \exp \left(z_{j} / T\right)} \]

其中超引數 T 是溫度，這是從統計力學中的玻爾茲曼分佈中借用的概念。如果將T設大，則Softmax之後的Logits數值，各個類別之間的概率分值差距會縮小，也即是強化那些非最大類別的存在感；反之，則會加大類別間概率的兩極分化。當T趨向於0時，softmax輸出將收斂為一個one-hot向量。當T趨向於無窮大時，softmax損失等價於MSE（當\(T\to \infty\)，用 \(1+x/T \to e^{x/T}\)來近似，再加上logits是零均值的假設，可推匯出該結論，具體見後文梯度公式推導），也就是擬合概率分佈變成了擬合logits。

logits經過Temperature影響的softmax之後得到的輸出相當於調節了logits的分佈。採用調節後的logits取代one-hot標籤，使得負標籤對應的非零logits也能參與交叉熵損失的計算。

Hinton論文中讓student去擬合調節後的歸一化的logits，並同時採用了標準的交叉熵損失作為聯合損失的一部分, λ 用於調節蒸餾Loss的影響程度。

\[L_{student}=CE(y, f(x)) + \lambda \cdot CE(\rm{Softmax}_T(z_t), \rm{Softmax}_T(z_s)) \]

注意，Softmax Temperature版的損失的數量級大約是原版的 \(1/T^2\)倍，因此如果想平衡兩個損失，可設定 \(\lambda=T^2\)。

在訓練新模型的時候，可以使用較高的 T 使得softmax產生的分佈足夠平緩，這時讓新模型（同樣溫度下）的softmax輸出近似原模型；在訓練結束以後再使用正常的溫度來預測。訓練過程中可以設定teacher annealing（退火），逐漸減少teacher暗知識的權重，讓student學習到一定程度之後不受teacher的限制。

化學意義

在化學中，蒸餾是一個有效的分離沸點不同的組分的方法，大致步驟是先升溫使低沸點的組分汽化，然後降溫冷凝，達到分離出目標物質的目的。在前面提到的這個過程中，我們先讓溫度升高，然後在測試階段恢復低溫，從而將原模型中的知識提取出來，因此將其稱為是蒸餾。

適用範圍

Logits蒸餾方法約束較少，同時適用於同構或異構的網路結構間的知識傳遞。異構網路如BERT與LSTM之間，參考 Distilled BiLSTM：Distilling Task-Specific Knowledge from BERT into Simple Neural Networks（2019），該論文提出了通過 BiLSTM 蒸餾BERT的方法，其思想與Hinton原始的logits蒸餾思想一致，蒸餾的結果弱於Bert但是比原始的雙向LSTM效果好很多。

Q：為什麼蒸餾需要提高溫度？

如果T為1，即原始的softmax，當teacher的預測logits兩級分化嚴重時softmax輸出與標籤接近，那麼 student 從蒸餾損失中就學不到額外的資訊了。而將T設定<1，則會使兩極分化更嚴重，因此需要設定 T>1。但是T也不能設定地太高，因為logit分值越低越不置信，過高的T反而引入噪聲。

Q：student只用soft target損失，不用hard target是否可以？

由於teacher模型一般不能達到完美的模型狀態，soft target僅是參考答案，可能存在錯誤，在傳授給student時會將student帶偏，而hard target則是標準答案，用來糾錯。

Q：如何解釋學生網路可能出現比教師網路精度更好的情況？

在學生網路引數量遠小於教師網路，並且學生網路不使用額外資料的前提下通常很難超過教師網路的精度，但是不盡然。

教師網路過擬合了，學生網路泛化更好（尤其在從多個教師網路學習的情況下，相當於專家系統投票平滑）
如果學生網路採用了新資料，那麼學生網路學習的資料分佈與教師網路不同，通過知識蒸餾，相當於用教師資料的分佈對學生網路進行了正則化約束，提高泛化能力。

特徵蒸餾方法

讓Student學習Teacher網路結構中的中間層特徵。最早採用這種模式的工作來自於自於論文：「FITNETS：Hints for Thin Deep Nets」，它強迫Student某些中間層的網路響應，要去逼近Teacher對應的中間層的網路響應。這種情況下，Teacher中間特徵層的響應，就是傳遞給Student的暗知識。

特徵蒸餾需要考慮的點包括：

中間層的特徵選取問題，如一般的DNN隱層、Transformer的Attention矩陣等；還需要考慮從哪些隱層選擇用於計算蒸餾損失。
損失函數的選擇：MSE、交叉熵、KL散度等。
以及不同的蒸餾策略，包括同時蒸餾多層、先蒸餾中間層再蒸餾最後一層、逐層蒸餾等。

下面介紹幾種典型的蒸餾方法。

BERT-PKD

BERT-PKD (Patient Knowledge Distillation for BERT Model Compression，EMNLP2019) 基於BERT-base蒸餾小型BERT，在中間的某些層上採用歸一化的MSE，再結合logits蒸餾方法。關於中間層的選擇，提出了兩種策略，一種是skip，用BERT-base的第[2,4,6,8,10]層，另一種是last，採用最後第[7,8,9,10,11]層。兩種策略實驗結果相差不大，skip 策略略好一點（<0.01）。

DistillBERT

多數蒸餾模型是對下游任務進行蒸餾，而 HuggingFace 提出的 DistilBERT, 論文：DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter（NIPS2019），則是在預訓練階段進行蒸餾。類似BERT-PKD，將層數減少了一半，基於12層的BERT-base，蒸餾6層的BERT student（用teacher模型引數初始化），同樣採用基本的損失函數（輸出層的logits softmax交叉熵損失，預訓練任務原本的MLM損失），不同之處在於隱層特徵蒸餾方式選用的cosine loss，用來調整教師和學生的隱層向量方向。

在該模型中，刪除了 token-type embeddings 和 pooler，並保持體系架構其餘部分不變，同時借鑑了 RoBERTa 論文中的一些訓練技巧。DistilBERT 與 BERT 相比保留了 95％以上的效能，但引數卻減少了 40％。

TinyBERT

TinyBERT: Distilling BERT for Natural Language Understanding: （華為諾亞方舟實驗室，EMNLP2019）提出了一種兩階段學習框架，包括通用蒸餾和特定任務蒸餾。相當於結合了BERT-PKD和DistillBERT，同時在預訓練和微調下游任務後做蒸餾，使得student達到了接近BERT-base的效能效果。TinyBERT對於隱層特徵，採用MSE；增加了Attention矩陣logits的MSE損失；增加了輸入embedding層的MSE。對於下游任務的微調，做了資料增廣來進一步提升蒸餾的效果。

實驗設定：預訓練階段只對中間層進行了蒸餾；下游任務微調階段先對中間層蒸餾20個epoch，再對最後一層蒸餾3個epoch。

在 GLUE 資料集上相對於 BERT-base，其效能並沒有下降多少，而推理引數小了 7.5 倍，推理時間快了 9.4 倍。

論文中比較重要的是Attention蒸餾方式，發現 BERT 學習的注意力權重可以捕獲大量的語言知識，而在 BERT 的現有知識蒸餾的方法（如 Distilled BiLSTM_SOFT，BERT-PKD 和 DistilBERT）中卻忽略了這一點。

為了靈活性，TinyBERT在計算隱層的特徵蒸餾損失時採用了一個變換矩陣，旨在將student的特徵變換到和teacher相同的空間中。這樣TinyBERT支援設計較小特徵維度的student網路，而BERT-PKD和DistillBERT的student都是和teacher具有相同的特徵維度，只是層數不同。

\[\mathcal L_{hidden} = MSE(H_SW_h, H_T) \]

輸入embedding層的MSE同樣採用了變換矩陣。

MobileBERT

MobileBERT: a Compact Task-Agnostic BERT for Resource-Limited Devices（Google brain，ACL2020）

MobileBERT 首先是在預訓練的模型結構上做壓縮，借鑑ResNet深層網路中採用的bottleneck結構（即先降維再升維），減少模型的引數量。結構圖和引數設定如下，其中圖(b)的結構是inverted-bottleneck，思路源自論文Mobilenet-v2: Inverted residuals and linear bottlenecks（2018）。可以看出MobileBERT充分借鑑了之前CV模型中thin&deep的發展路徑。

論文對Bottleneck的應用方式是在transformer block的輸入輸出各加入一個線性層，實現維度的縮放。採用加入inverted-bottleneck的BERT-large作為教師模型，加入bottleneck的相同層數但是維度數減少的BERT作為學生模型。在預訓練階段蒸餾之後，直接用蒸餾預訓練模型在下游任務上微調，同DistillBERT。

在BERT中Attention模組之後緊跟FFN來增加非線性，並且每個block中層數比固定為1:2，但在引入bottleneck之後單層FFN的引數量大大減少，繼續用2層的FFN非線效能力變弱，因此對FFN模組增加了層數，論文采用了固定值4。

損失函數：預訓練任務（MLM+NSP）+中間層MSE+Attention Prob KL散度。

論文實驗了不同的蒸餾策略，包括同時蒸餾多層、先蒸餾中間層再蒸餾最後一層、逐層蒸餾，發現逐層蒸餾略勝一籌。

此外，為了在嵌入式移動裝置上提速，通過分析運算元的執行耗時，選擇了替換兩個運算元：

LayerNorm -> NoNorm，取消LayerNorm中的normalization，保留線性變換的部分。
gelu -> relu，減少了erf() 函數的計算。

整體模型的預測耗時對比如下：

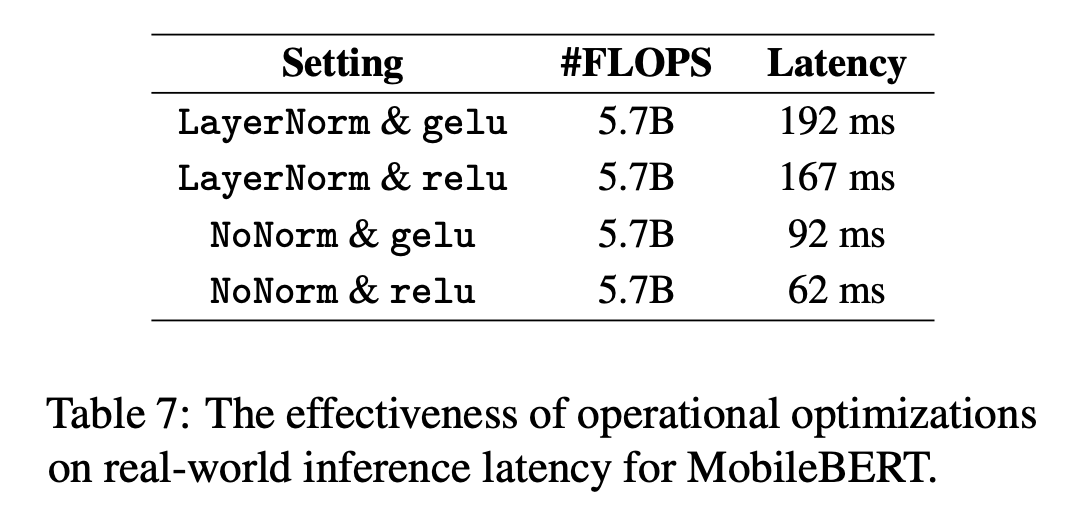
效果：MobileBERT在保留24層的情況下，相比BERT-base減少了4.3倍的引數，速度提升5.5倍，在GLUE上平均只比BERT-base低了0.6個點，在 Pixel 4 手機上執行耗時62ms。

MiniLM

MiniLM: Deep Self-Attention Distillation for Task-Agnostic Compression of Pre-Trained Transformers（MSRA，2020）

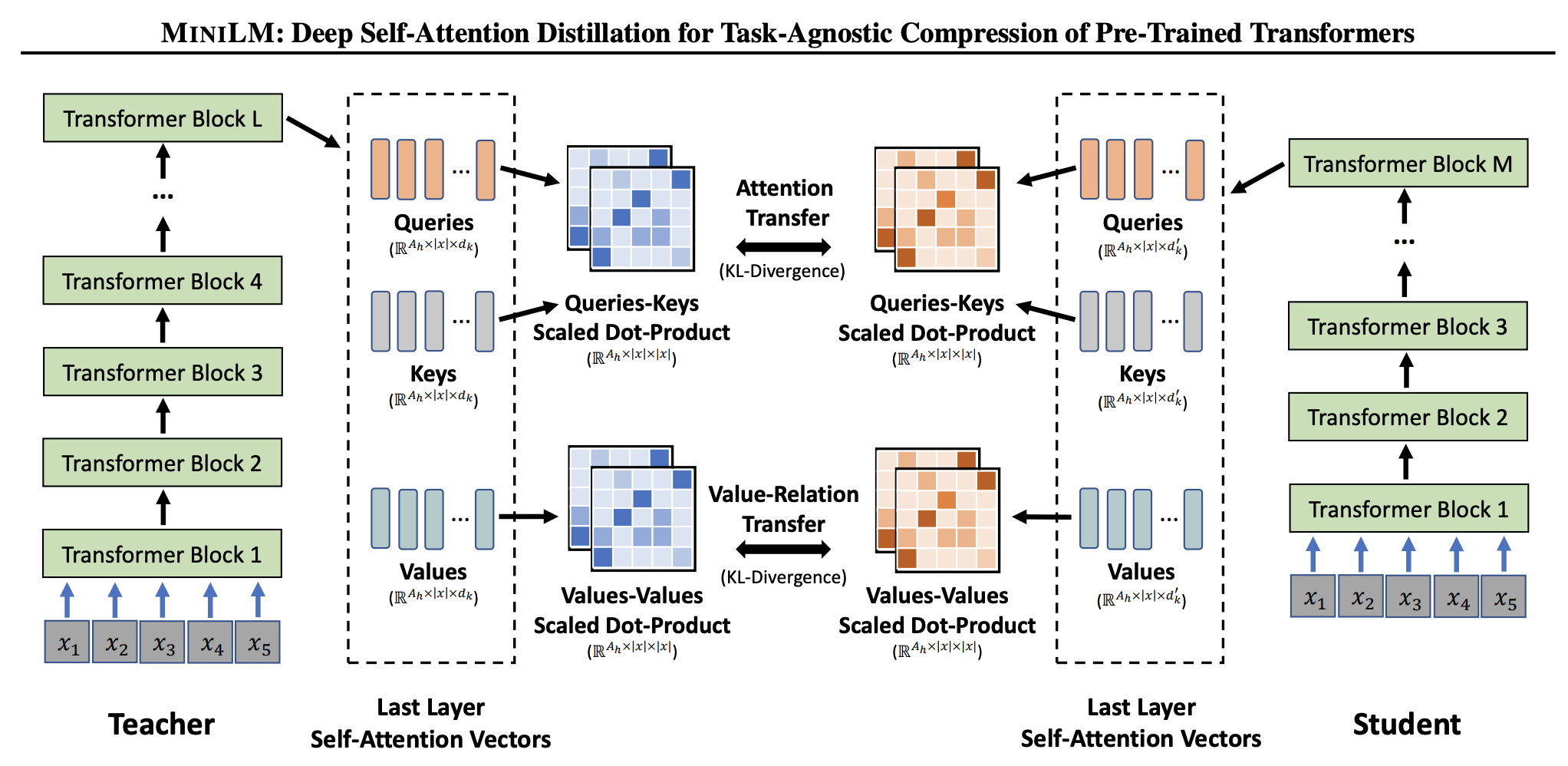
損失函數設計：

MiniLM也採用了和TinyBERT相同的Attention Prob KL散度損失，但僅應用於最後一層，這樣的簡化給模型設計帶來靈活性，不必在teacher-student layer對映的選擇上下功夫。
新增一個Value-Relation map的KL散度，計算方式類似Attention的softmax(Query*Key/sqrt(d)) -> softmax(Val*Val/sqrt(d)) ，在Transformer encoder中Query、Key、Val是對同一值採用了不同的變換矩陣對映到不同的值，Val-Relation能表示不同token之間的一些關係，用來補充Attention的關係。這裡可能欠缺一個可解釋性。

Attention和Value-Relation map都是與文字輸入長度有關，但與特徵維度無關的，因此student可以設定與teacher不同的維度。

MiniLM與UniLM屬於同一團隊，程式碼開源在UniLM倉庫中。對於生成式任務，可以採用UniLM來做蒸餾。

總結前面介紹的幾個模型：

任務	預訓練	.	.	.	.	下游任務微調	.	.	.
蒸餾方法\layers	Embedding層	Attention	Value-Relation	隱層	輸出預測層	Embedding層	Attention	隱層	輸出預測層
Distilled BiLSTM									MSE
BERT-PKD								MSE	CE
DistillBERT				cosine	CE
TinyBERT	MSE	MSE		MSE		MSE	MSE	MSE	CE
MobileBERT		KL		MSE	MSE
MiniLM		KL	KL

聯合訓練方法

除了常規的兩階段分步驟訓練的方式（先訓練teacher再訓練student），還可以像雙塔結構一樣聯合訓練。兩個網路之間共用底層特徵，如embedding lookup特徵，相當於右側網路使用了copy and freeze的特徵遷移正規化，這樣知識蒸餾地可能更充分一些。

這種聯合訓練方法在論文 "Rocket Launching: A Universal and Efficient Framework for Training Well-performing Light Net"（阿里媽媽）中被提出，用於精排模型。

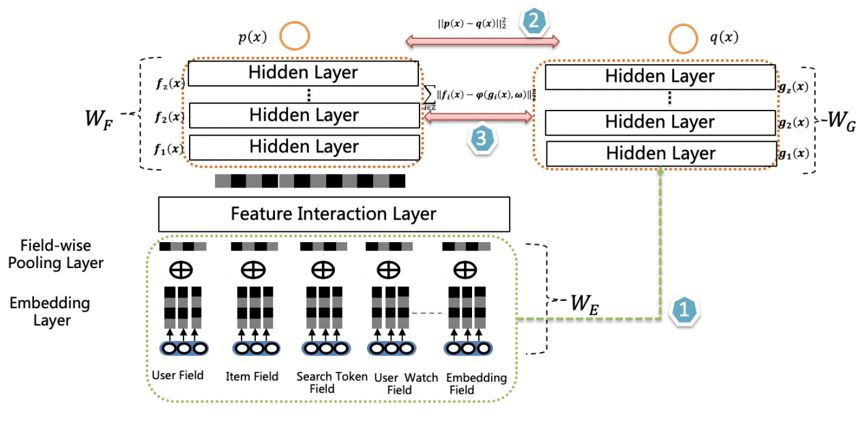
愛奇藝也提出了一種雙塔蒸餾的排序模型，相比Rocket Launching，增加了特徵蒸餾，即在損失中加入中間層的特徵差異。為了增加teacher的複雜度，在輸入層後新增了特徵互動層（Feature Interaction Layer）。

雙DNN排序模型結構如下，由兩個DNN CTR Model組成，右側是Student，Student 模型是最終用於上線推理的CTR 模型。相比 Teacher 模型推理速度提高5倍，模型大小縮小2倍。

參考：

附

標籤平滑（Label Smoothing）

標籤平滑歸一化：Label Smoothing Regularization (LSR)

LSR是一種通過在輸出y中新增噪聲，實現對模型進行約束，降低模型過擬合（overfitting）程度的一種約束方法（regularization methed）。

one hot存在的問題：

丟失了類內、類間關聯
對於模稜兩可的樣本表徵較差
使模型容易學的過於自信，容易過擬合
對噪聲標籤（錯誤標註資料）敏感

例如採用01標籤的訓練資料計算交叉熵損失時損失值只與非0項相關，

\[H(\boldsymbol{y}, \boldsymbol{p})=\sum_{k=1}^{K}-y_{k} \log \left(p_{k}\right) \]

LSR的優化方式為對「硬目標」進行「軟化」，標籤平滑的定義為：

\[y_{k}^{L S}=y_{k}(1-\alpha)+\alpha / K \]

將one hot中的0改為 \(\alpha/K\) ，其中K為類別數，1改為\(1-\alpha+\alpha/K\), 總和仍然為1. 超引數α通常取0.1。

簡單地說，標籤平滑是將真實的one hot標籤做一個標籤平滑處理，使得標籤變成soft label。

軟化有什麼好處？

從函數曲線來看，約往1靠近，函數值變化越慢，也越難優化（交叉熵損失中的log曲線與sigmoid類似，靠近1時到達飽和區）。通過降低預測目標（soft label），保證優化過程始終處於優化效率最高的中間區域，避免進入飽和區。

適用場景

hinton的這篇[when does label smoothing help? ]論文從另一個角度去解釋了 label smoothing的作用：

多分類可能更有效果，類別更緊密，不同類別分的更開；小類別可能效果弱一些。

注：在知識蒸餾中的teacher模型通常不使用標籤平滑。而知識蒸餾方法中採用soft target的方式正好相當於標籤平滑。hinton在論文中說了一些原因：標籤平滑丟失了一些資訊，泛化有利於教師網路的效能，但是它傳遞給學生網路的資訊更少。但是這篇 ICLR 2021論文 IS LABEL SMOOTHING TRULY INCOMPATIBLE WITH KNOWLEDGE DISTILLATION: AN EMPIRICAL STUDY 提出了不同的觀點：標籤平滑和知識蒸餾並不衝突，針對不同的場景和任務，需要的teacher型別也不盡相同，但大體上來說，精度越高的網路，通常可以蒸餾出更強的student。

knowledge distillation相比於label smoothing，最主要的差別在於，知識蒸餾的soft label是通過網路推理得到的，而label smoothing的soft label是人為設定的。

原始訓練模型的做法是讓模型的softmax分佈與真實標籤進行匹配，而知識蒸餾方法是讓student模型與teacher模型的softmax分佈進行匹配。直觀來看，後者比前者具有這樣一個優勢：經過訓練後的原模型，其softmax分佈包含有一定的知識——真實標籤只能告訴我們，某個影象樣本是一輛寶馬，不是一輛垃圾車，也不是一顆蘿蔔；而經過訓練的softmax可能會告訴我們，它最可能是一輛寶馬，不大可能是一輛垃圾車，但絕不可能是一顆蘿蔔。

知識蒸餾得到的soft label相當於對資料集的有效資訊進行了統計，保留了類間的關聯資訊，剔除部分無效的冗餘資訊。 相比於label smoothing，模型在資料集上訓練得到的soft label更加可靠。

參考：

Google Brain最新論文：標籤平滑何時才是有用的？https://www.jiqizhixin.com/articles/2019-07-09-7
從標籤平滑和知識蒸餾理解Soft Label https://jishuin.proginn.com/p/763bfbd66830
Müller R, Kornblith S, Hinton G. When Does Label Smoothing Help?[J]. arXiv preprint arXiv:1906.02629, 2019.
https://cloud.tencent.com/developer/article/1853009

附-Softmax Temperature梯度推導

\[\begin{align} q_i &=\frac{\exp(z_i/T)}{\sum_j\exp(z_j/T)} \\ L &= - \sum_i p_i\log q_i \\ {\partial L \over \partial z_i} &= -{p_i\over q_i} {\partial q_i \over \partial z_i} - \sum_{j\ne i}{p_j\over q_j}{\partial q_j \over \partial z_i} \\ &= -{1\over T} \left( {p_i\over q_i}(q_i-q_i^2) + \sum_{j\ne i} {p_j\over q_j} \cdot -q_iq_j \right) = -{1\over T} \left( p_i(1-q_i) -q_i(1-p_i) \right) \\ &= {1\over T} \left( q_i-p_i \right) \\ \end{align} \]

當\(T\to \infty\)，用 \(1+x/T \to e^{x/T}\)來近似，假設logits均值為0，設teacher模型的logit為 \(v_i\)，那麼有 \(q_i\approx{1+z_i/T\over N}, p_i\approx{1+v_i/T\over N}, {\partial L \over \partial z_i}\approx {1\over NT^2}(z_i-v_i)\). 這等價於最小化MSE：\(1/2 (z_i-v_i)^2\)，對\(z_i\)的梯度為 \(z_i-v_i\).

注意到 \({\partial L \over \partial z_i}\approx {1\over NT^2}(z_i-v_i)\)式中分母包含\(T^2\)，這也是Softmax Temperature版的損失的數量級大約是原版的 \(1/T^2\)倍的由來。

附-KL散度、交叉熵損失關係

KL散度定義如下

\[\begin{align} D_{KL}(p∣∣q) &=E[\log p(x)−\log q(x)] \\ &=E[\log{1\over q(x)} - \log{1\over p(x)}] \\ &=\sum^N_i p(x_i)\cdot [\log{1\over q(x_i)} - \log{1\over p(x_i)}] \\ &=H(p,q)-H(p) \end{align} \]

這裡的 \(p\) 是真實分佈，\(q\) 是預測分佈。衡量的是給定分佈偏離真實分佈的程度，取值範圍 \([0, +\infty)\)。KL 散度越小，分佈之間的匹配就越好。如果兩個分佈完全匹配，KL散度為0。

真實分佈與預測分佈的KL散度等價於兩者的交叉熵減去真實分佈的資訊熵。

真實分佈 \(p\) 確定的情況下熵 \(H(p)\) 是一個定值，對於模型來說是一個不可優化的常數項，對模型優化沒有影響，因此優化交叉熵和優化KL散度（即預測標籤的分佈與真實標籤分佈的差異）是等價的，並且對於多分類的one hot標籤來說：\(H(p)=0\)。但是當兩個分佈p、q相等時交叉熵 \(H(p,q)=H(p)\ne 0\)，這樣損失不為0，模型可能總是保持學習狀態。
如果目標真實分佈是有顯著變化的，那麼就不適合用交叉熵。比如mini-batch設定為1，那麼 \(H(p)\) 會變化較大，而且交叉熵損失會隨著mini-batch的變化而振盪。但通常mini-batch不會設太小，真實分佈接近不變，不太影響模型的學習。

在蒸餾模型中用KL散度、交叉熵的都有，hinton的logits蒸餾方式正是交叉熵。

蒸餾工具

哈工大訊飛聯合實驗室的蒸餾工具TextBrewer：airaria/TextBrewer: A PyTorch-based knowledge distillation toolkit for natural language processing