我真的想知道,AI框架跟計算圖什麼關係?PyTorch如何表達計算圖?
目前主流的深度學習框架都選擇使用計算圖來抽象神經網路計算表達,通過通用的資料結構(張量)來理解、表達和執行神經網路模型,通過計算圖可以把 AI 系統化的問題形象地表示出來。
本節將會以AI概念落地的時候,遇到的一些問題與挑戰,因此引出了計算圖的概念來對神經網路模型進行統一抽象。接著展開什麼是計算,計算圖的基本構成來深入瞭解誒計算圖。最後簡單地學習PyTorch如何表達計算圖。
視訊、文章、PPT都開源在:chenzomi12.github.io
AI系統化問題
遇到的挑戰
在真正的 AI 工程化過程中,我們會遇到諸多問題。而為了高效地訓練一個複雜神經網路,AI 框架需要解決許多問題,例如:
- 如何對複雜的神經網路模型實現自動微分?
- 如何利用編譯期的分析 Pass 對神經網路的具體執行計算進行化簡、合併、變換?
- 如何規劃基本計算 Kernel 在計算加速硬體 GPU/TPU/NPU 上高效執行?
- 如何將基本處理單元派發(Dispatch)到特定的高效後端實現?
- 如何對通過神經網路的自動微分(反向傳播實現)衍生的大量中間變數,進行記憶體預分配和管理?
為了使用用統一的方式,解決上述提到的挑戰,驅使著 AI 框架的開發者和架構師思考如何為各類神經網路模型的計算提供統一的描述,從而使得在執行神經網路計算之前,能夠對整個計算過程儘可能進行推斷,在編譯期間自動為深度學習的應用程式補全反向計算、規劃執行、降低執行時開銷、複用和節省記憶體。能夠更好地對特定領域語言(DSL),這裡特指深度學習和神經網路進行表示,並對使用 Python 編寫的神經網路模型進行優化與執行。
因此派生出了目前主流的深度學習框架都選擇使用計算圖來抽象神經網路計算。
計算圖的定義
我們會經常遇到有些 AI 框架把統一的圖描述稱為資料流圖,有些稱為計算圖,這裡可以統稱為計算圖。下面簡單介紹為什麼可以都統稱為計算圖的原因。
- 資料流圖(Data Flow Diagram,DFD):從資料傳遞和加工角度,以圖形方式來表達系統的邏輯功能、資料在系統內部的邏輯流向和邏輯變換過程,是結構化系統分析方法的主要表達工具及用於表示軟體模型的一種圖示方法。在 AI 框架中資料流圖表示對資料進行處理的單元,接收一定的資料輸入,然後對其進行處理,再進行系統輸出。
- 計算圖(Computation Graph):被定義為有向圖,其中節點對應於數學運算,計算圖是表達和評估數學表示式的一種方式。而在 AI 框架中,計算圖就是一個表示運算的有向無環圖(Directed Acyclic Graph,DAG)。
其兩者都把神經網路模型統一表示為圖的形式,而圖則是由節點和邊組成。其都是在描述資料在圖中的節點傳播的路徑,是由固定的計算節點組合而成,資料在圖中的傳播過程,就是對資料進行加工計算的過程。下面以公式為例:
f(x1,x2)=ln(x1)+x1x2−sin(x2)
對上述公式轉換為對應的計算圖。
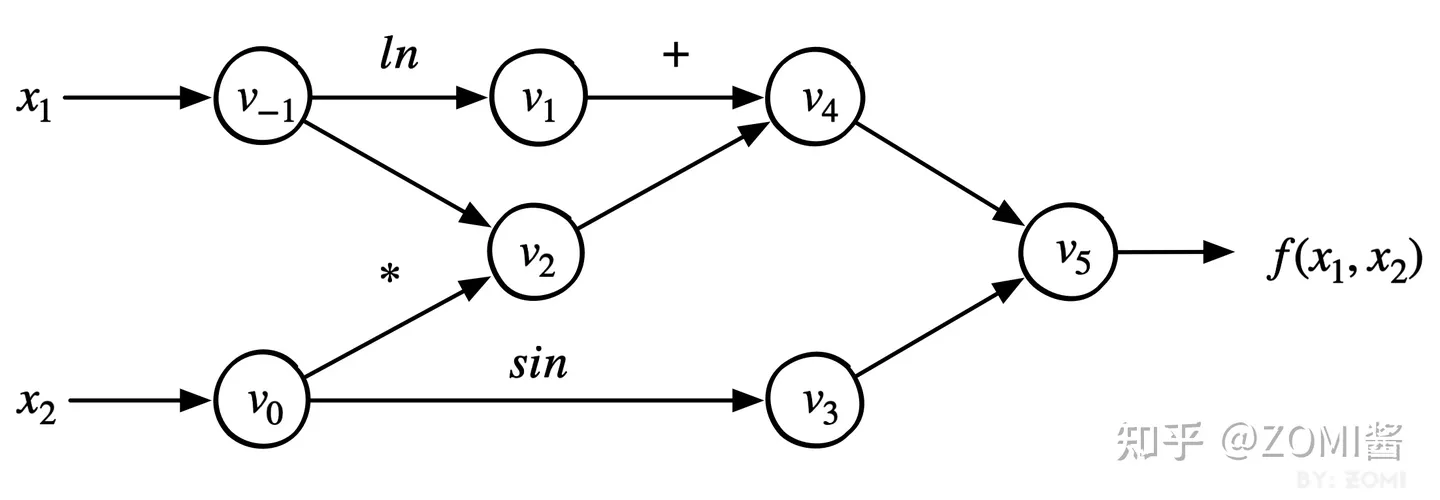
計算圖的基本構成
資料表達方式
- 標量 Scalar
標量(scalar),亦稱「無向量」。有些物理量,只具有數值大小,而沒有方向,部分有正負之分,物理學上指有大小而沒有方向的量(跟「向量」相區別)。物理學中,標量(或作純量)指在座標變換下保持不變的物理量。用通俗的說法,標量是隻有大小,沒有方向的量,如功、體積、溫度等。
在 AI 框架或者計算機中,標量是一個獨立存在的數,比如線性代數中的一個實數 488 就可以被看作一個標量,所以標量的運算相對簡單,與平常做的算數運算類似。程式碼 x 則作為一個標量被賦值。
x = 488- 向量 Vector
向量(vector),物理、工程等也稱作向量、歐幾里得向量(Euclidean vector),是數學、物理學和工程科學等多個自然科學中的基本概念。指一個同時具有大小和方向,且滿足平行四邊形法則的幾何物件。理論數學中向量的定義為任何在稱為向量空間的代數結構中的元素。
在 AI 框架或者計算機中,向量指一列順序排列的元素,通常習慣用括號將這些元素擴起來,其中每個元素都又一個索引值來唯一的確定其中在向量中的位置。其有大小也有方向,以公式為例,其程式碼 x_vec 則被作為一個向量被賦值。
xvec=[1.12.23.3]
x_vec = [1.1, 2.2, 3.3]- 矩陣 Matrix
矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等代數學中的常見工具,也常見於統計分析等應用數學學科中。
在機器學習領域經常被使用,比如有 N 個使用者,每個使用者有 M 個特徵,那這個資料集就可以用一個 NxM 的矩陣表示,在折積神經網路中輸入模型的最初的資料是一個圖片,讀取圖片上的畫素點(Pixel)作為輸入,一張尺寸大小為 256x256 的圖片,實質上就可以用 256*256 的矩陣進行表示。
以公式為例,其程式碼 x_mat 則被表示為一個矩陣被賦值。
xmat=[123456789]
x_mat = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]圖中對標量、向量、矩陣進行形象化表示:

張量
張量(tensor)理論是數學的一個分支學科,在力學中有重要應用。張量這一術語起源於力學,它最初是用來表示彈性媒介中各點應力狀態的,後來張量理論發展成為力學和物理學的一個有力的數學工具。張量之所以重要,在於它可以滿足一切物理定律必須與座標系的選擇無關的特性。張量概念是向量概念的推廣,向量是一階張量。
在幾何代數中,張量是基於向量和矩陣的推廣,通俗一點理解的話,可以將標量是為零階張量,向量視為一階張量,矩陣視為二階張量。在 AI 框架中,所有資料將會使用張量進行表示,例如,影象任務通常將一副圖片根據組織成一個3維張量,張量的三個維度分別對應著影象的長、寬和通道數,一張長和寬分別為 H, W 的彩色的圖片可以表示為一個三維張量,形狀為 (C, H, W)。自然語言處理任務中,一個句子被組織成一個2維張量,張量的兩個維度分別對應著詞向量和句子的長度。
一組影象或者多個句子只需要為張量再增加一個批次(batch)維度,N 張彩色圖片組成的一批資料可以表示為一個四維張量,形狀為 (N, C, H, W)。
張量和張量操作
在執行計算任務中,資料常常被組織成一個高維陣列,整個計算任務的絕大部分時間都消耗在高維陣列上的數值計算操作上。高維陣列和高維陣列之上的數值計算是神經網路的核心,構成了計算圖中最重要的一類基本運算元。在 AI 框架的資料中主要有稠密張量和稀疏張量,這裡先考慮最為常用的稠密張量。
張量作為高維陣列,是對標量,向量,矩陣的推廣。AI 框架對張量的表示主要有以下幾個重要因素:
- 元素資料型別:在一個張量中,所有元素具有相同的資料型別,如整型,浮點型,布林型,字元型等資料型別格式
- 形狀:張量每個維度具有固定的大小,其形狀是一個整型數的元組,描述了一個張量的維度以及每個維度的長度
- 裝置:決定了張量的儲存裝置,如在通用處理器 CPU 中的 DDR 上還是 GPU/NPU 的 HBM 上等。
下面是針對形狀為 (3, 2, 5) 的三維張量進行表示。
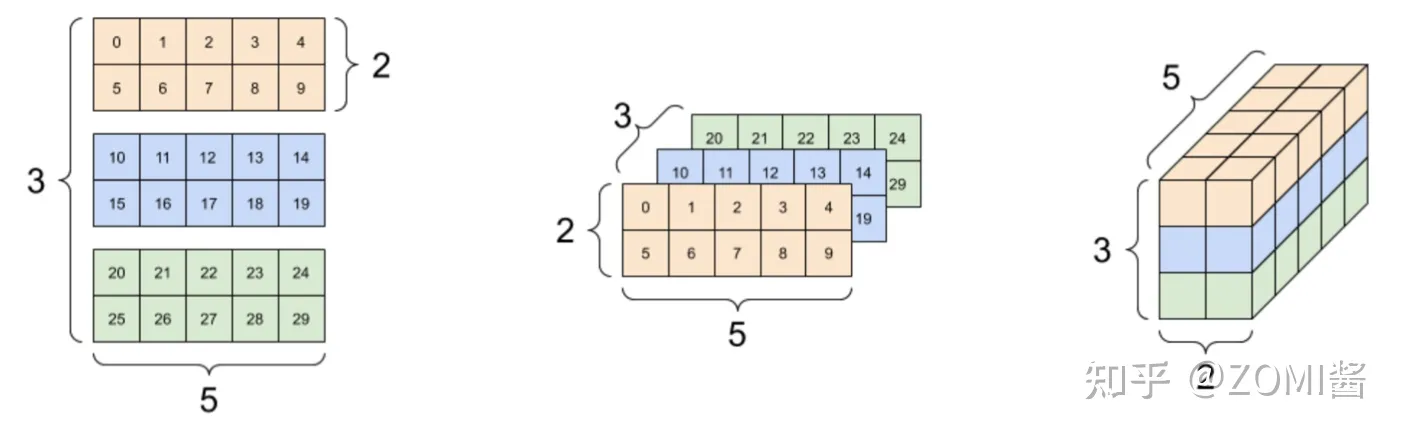
雖然張量通常用索引來指代軸,但是始終要記住每個軸的含義。軸一般按照從全域性到區域性的順序進行排序:首先是批次軸,隨後是空間維度,最後是每個位置的特徵。這樣,在記憶體中,特徵向量就會位於連續的區域。例如針對形狀為 (3, 2, 4, 5) 的四維張量進行表示,其記憶體表示如圖中右側所示。
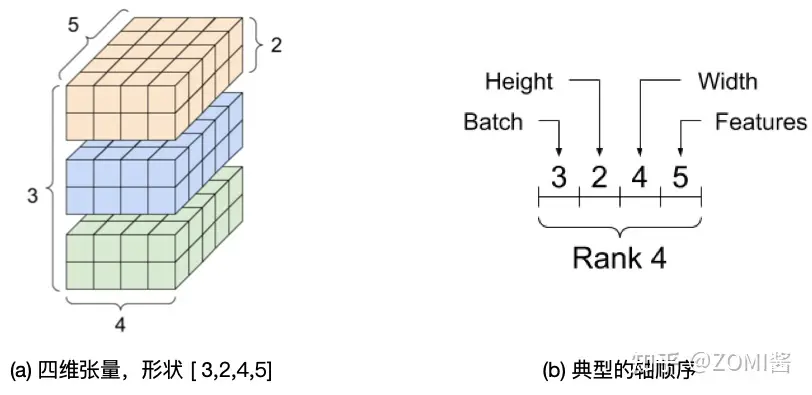
高維陣列為開發者提供了一種邏輯上易於理解的方式來組織有著規則形狀的同質資料,極大地提高了程式設計的可理解性。另一方面,使用高維資料組織資料,易於讓後端自動推斷並完成元素邏輯儲存空間向物理儲存空間的對映。更重要的是:張量操作將同構的基本運算型別作為一個整體進行批次操作,通常都隱含著很高的資料並行性,因此非常適合在單指令多資料(SIMD)並行後端上進行加速。
計算圖表示AI框架
計算圖是用來描述運算的有向無環圖,有兩個主要元素:節點 (Node) 和邊 (Edge)。節點表示資料,如向量、矩陣、張量;邊表示具體執行的運算,如加、減、乘、除和折積等。
下面以簡單的數學公式 $z = x + y$ 為例,可以繪製上述方程的計算圖如下:
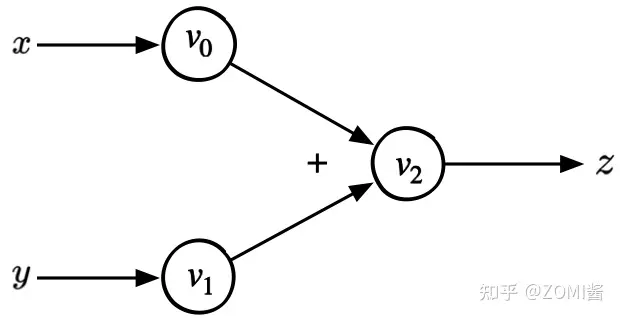
上面的計算圖具有一個三個節點,分別代表張量資料中的兩個輸入變數 x 和 y 以及一個輸出 z。兩條邊帶有具體的 「+」 符號表示加法。
在 AI 框架中會稍微有點不同,其計算圖的基本組成有兩個主要的元素:1)基本資料結構張量和2)基本計算單元運算元。節點代表 Operator 具體的計算操作(即運算元),邊代表 Tensor 張量。整個計算圖能夠有效地表達神經網路模型的計算邏輯和狀態。
- 基本資料結構張量:張量通過 shape 來表示張量的具體形狀,決定在記憶體中的元素大小和元素組成的具體形狀;其元素型別決定了記憶體中每個元素所佔用的位元組數和實際的記憶體空間大小
- 基本運算單元運算元:具體在加速器 GPU/NPU 中執行運算的是由最基本的代數運算元組成,另外還會根據深度學習結構組成複雜運算元。每個運算元接受的輸入輸出不同,如Conv運算元接受3個輸入Tensor,1個輸出Tensor
下面以簡單的一個折積、一個啟用的神經網路模型的正向和反向為例,其前向的計算公式為:
f(x)=ReLU(Conv(w,x,b))
反向計算微分的時候,需要加上損失函數:
Loss(x,x′)=f(x)−x′
根據正向的神經網路模型定義,AI 框架中的計算圖如下:
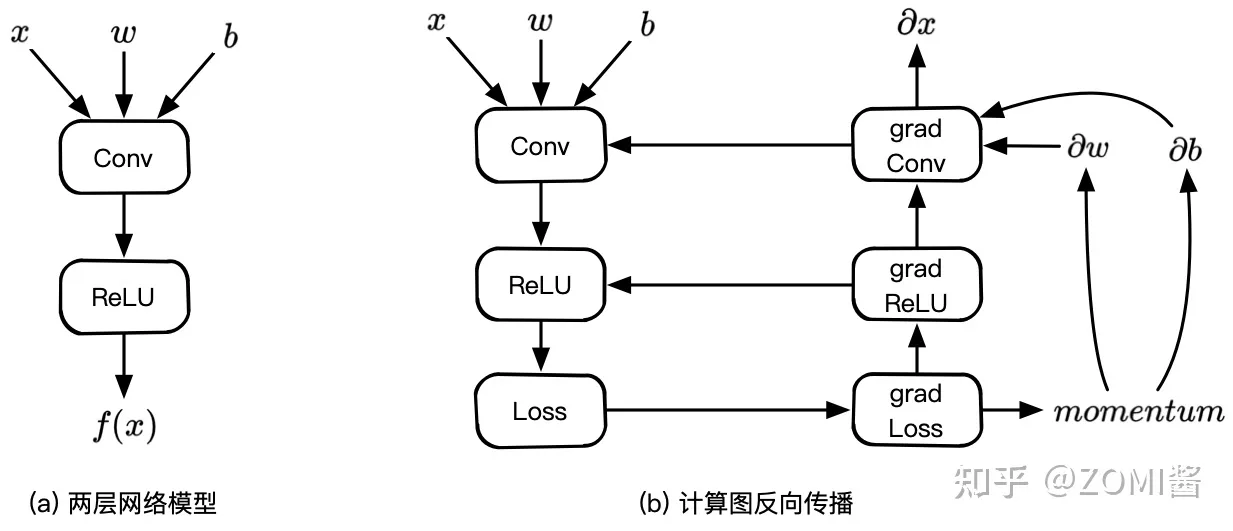
上面 (a) 中計算圖具有兩個節點,分別代表折積 Conv 計算和啟用 ReLU 計算,Conv 計算接受三個輸入變數 x 和權重 w 以及一個偏置 b,啟用接受 Conv 折積的輸出並輸出一個變數。(b)為對應(a)的反向計算圖,在神經網路模型訓練的過程當中,自動微分功能會為開發者自動構建反向圖,然後輸入輸出完整一個完整step計算。
總而言之,AI 框架的設計很自然地沿用了張量和張量操作,將其作為構造複雜神經網路的基本描述單元,開發者可以在不感知複雜的框架後端實現細節的情況下,在 Python 指令碼語言中複用由後端優化過的張量操作。而計算 Kernel 的開發者,能夠隔離神經網路演演算法的細節,將張量計算作為一個獨立的效能域,使用底層的程式設計模型和程式語言應用硬體相關優化。
在這裡的計算圖其實忽略了2個細節,特殊的操作:如:程式程式碼中的 For/While 等構建控制流;和特殊的邊:如:控制邊表示節點間依賴。
PyTorch計算圖
動態計算圖
在Pytorch的計算圖中,同樣由節點和邊組成,節點表示張量或者函數,邊表示張量和函數之間的依賴關係。其中Pytorch中的計算圖是動態圖。這裡的動態主要有兩重含義。
- 第一層含義是:計算圖的正向傳播是立即執行的。無需等待完整的計算圖建立完畢,每條語句都會在計算圖中動態新增節點和邊,並立即執行正向傳播得到計算結果。
import torch
w = torch.tensor([[3.0,1.0]],requires_grad=True)
b = torch.tensor([[3.0]],requires_grad=True)
X = torch.randn(10,2)
Y = torch.randn(10,1)
# Y_hat定義後其正向傳播被立即執行,與其後面的loss建立語句無關
Y_hat = [email protected]() + b
print(Y_hat.data)
loss = torch.mean(torch.pow(Y_hat-Y,2))
print(loss.data)- 第二層含義是:計算圖在反向傳播後立即銷燬。下次呼叫需要重新構建計算圖。如果在程式中使用了backward方法執行了反向傳播,或者利用torch.autograd.grad方法計算了梯度,那麼建立的計算圖會被立即銷燬,釋放儲存空間,下次呼叫需要重新建立。
# 如果再次執行反向傳播將報錯
loss.backward()
# 計算圖在反向傳播後立即銷燬,如果需要保留計算圖, 需要設定retain_graph = True
loss.backward(retain_graph = True)計算圖中Function
計算圖中的另外一種節點是Function, 實際上為對張量操作的函數,其特點為同時包括正向計算邏輯和反向傳播的邏輯。通過繼承torch.autograd.Function來建立。
以建立一個ReLU函數為例:
class MyReLU(torch.autograd.Function):
# 正向傳播邏輯,可以用ctx存輸入張量,供反向傳播使用
@staticmethod
def forward(ctx, input):
ctx.save_for_backward(input)
return input.clamp(min=0)
#反向傳播邏輯
@staticmethod
def backward(ctx, grad_output):
input, = ctx.saved_tensors
grad_input = grad_output.clone()
grad_input[input < 0] = 0
return grad_input接著在構建動態計算圖的時候,加入剛建立的Function節點。
# relu現在也可以具有正向傳播和反向傳播功能
relu = MyReLU.apply
Y_hat = relu([email protected]() + b)
loss = torch.mean(torch.pow(Y_hat-Y,2))
loss.backward()
print(w.grad)
print(b.grad)
print(Y_hat.grad_fn)
tensor([[4.5000, 4.5000]])
tensor([[4.5000]])
<torch.autograd.function.MyReLUBackward object at 0x1205a46c8>總結
- 瞭解AI應用或者深度學習需要工程化、系統化過程中會遇到哪些問題
- 計算圖的提出,解決了AI系統向下硬體執行計算統一表示,向上承接AI相關程式表示
- 瞭解了計算圖的基本構成是由獨立的資料結構張量和基本計算單元運算元組成