2023-07-22：一共有n個專案，每個專案都有兩個資訊，

projects[i] = {a, b}，

表示i號專案做完要a天，但是當你投入b個資源，它就會縮短1天的時間，

你一共有k個資源，你的目標是完成所有的專案，但是希望總天數儘可能縮短。

在所有專案同時開工的情況下，返回儘可能少的天數。

1 <= n <= 10^5，

1 <= k <= 10^7。

答案2023-07-22：

以下是程式碼的大致過程和功能描述：

1.匯入所需的包：fmt 用於列印輸出，math 用於數學運算。

2.定義函數 minDays，該函數接受專案詳情和可用資源數量作為輸入引數。

3.初始化變數 l 和 r，用於跟蹤搜尋範圍的左右邊界。

4.遍歷專案列表，並更新 r 的值為當前 r 和專案完成時間 (project[0]) 中的最大值。

5.將變數 m 和 ans 初始化為 r，作為找到的目標最少天數的初始猜測。

6.使用二分搜尋演演算法找到最小天數。重複以下步驟，直到 l 小於等於 r：

• 計算中間值 m，即 l 和 r 的平均值。

• 如果在 m 天或更少的時間內完成所有專案所需的總資源量 (yeah(projects, m)) 小於等於可用資源量 k，則更新 ans 為 m，並將右邊界 r 調整為 m - 1。

• 否則，將左邊界 l 調整為 m + 1。

7.返回 ans 的最終值，表示完成所有專案所需的最少天數。

8.定義 yeah 函數，該函數接受專案詳情和天數作為輸入引數。

9.初始化變數 ans，用於跟蹤所有需要的資源總量。

10.遍歷專案列表，並計算超過給定天數的每個專案所需的資源量。

11.將每個專案所需的資源量新增到 ans。

12.返回 ans 的最終值，表示超過給定天數的所有專案所需的資源總量。

13.在 main 函數中，建立一個範例專案資料集 project，其中包含專案的詳細資訊。

14.將可用資源 k 設定為特定值。

15.列印呼叫 minDays 函數並傳入專案資料集和可用資源作為引數的結果。

總的時間複雜度：

• minDays 函數中的二分搜尋演演算法的時間複雜度為 O(log(r))，其中 r 是最大專案完成時間。

• yeah 函數中的遍歷專案列表的時間複雜度為 O(n)，其中 n 是專案的數量。

因此，總的時間複雜度為 O(log(r) + n)。

總的空間複雜度：

• 空間複雜度主要來自於變數的儲存和函數呼叫的堆疊空間。

• 不考慮輸入資料的空間佔用，變數和資料結構的空間複雜度是常數級的，不隨輸入規模的增長而變化。

• 函數呼叫的堆疊空間複雜度是 O(log(r) + n)，其中 r 是最大專案完成時間，n 是專案的數量。

因此，總的空間複雜度可以近似為 O(log(r) + n)。

go完整程式碼如下：

package main

import (
	"fmt"
	"math"
)

func minDays(projects [][]int, k int) int {
	l := 0
	r := 0
	for _, project := range projects {
		r = int(math.Max(float64(r), float64(project[0])))
	}
	m, ans := r, r
	for l <= r {
		m = (l + r) / 2
		if yeah(projects, m) <= k {
			ans = m
			r = m - 1
		} else {
			l = m + 1
		}
	}
	return ans
}

func yeah(projects [][]int, days int) int {
	ans := 0
	for _, p := range projects {
		if p[0] > days {
			ans += (p[0] - days) * p[1]
		}
	}
	return ans
}

func main() {
	project := [][]int{{1, 2}, {3, 4}, {5, 6}}
	k := 4
	fmt.Println(minDays(project, k))
}

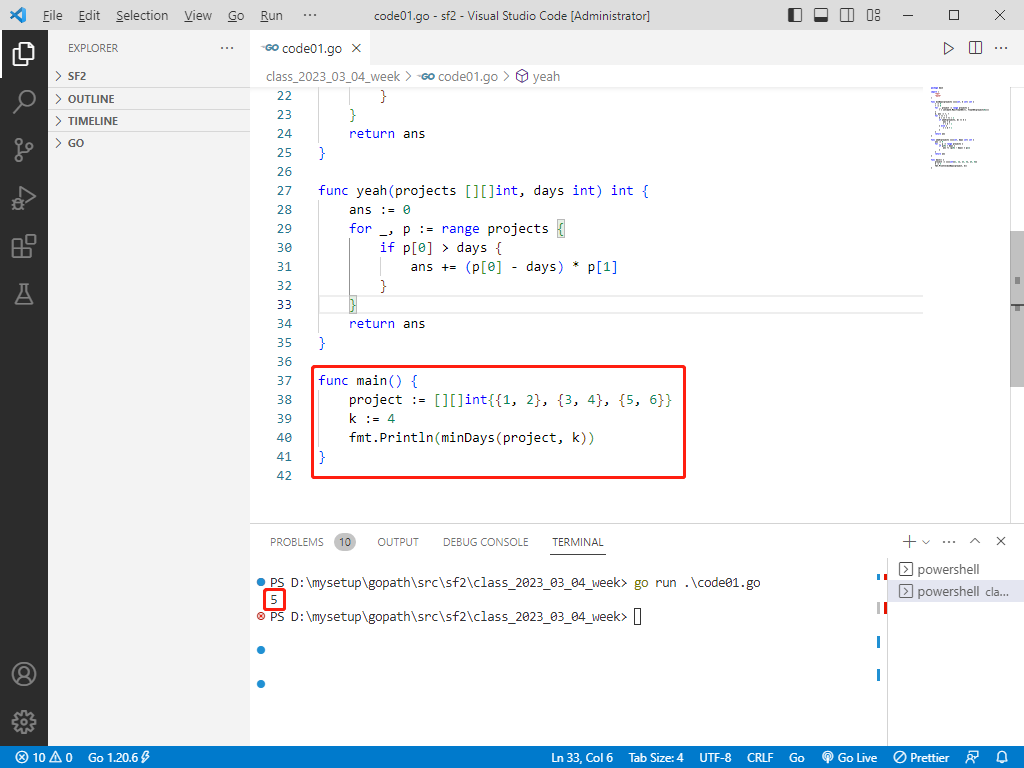
rust完整程式碼如下：

fn main() {
    let project = vec![vec![1, 2], vec![3, 4], vec![5, 6]];
    let k = 4;
    println!("{}", min_days(&project, k));
}

fn min_days(projects: &Vec<Vec<i32>>, k: i32) -> i32 {
    let mut l = 0;
    let mut r = 0;
    for project in projects {
        r = r.max(project[0]);
    }
    let mut ans = r;
    while l <= r {
        let m = (l + r) / 2;
        if yeah(projects, m) <= k {
            ans = m;
            r = m - 1;
        } else {
            l = m + 1;
        }
    }
    ans
}

fn yeah(projects: &Vec<Vec<i32>>, days: i32) -> i32 {
    let mut ans = 0;
    for p in projects {
        if p[0] > days {
            ans += (p[0] - days) * p[1];
        }
    }
    ans
}

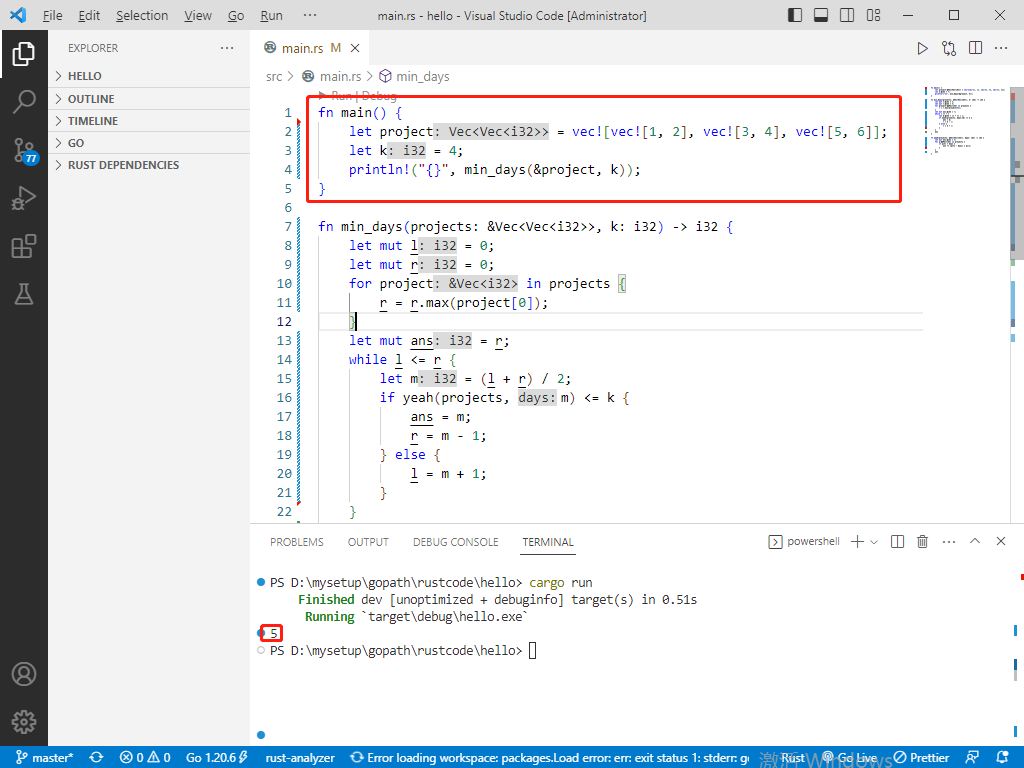
c++完整程式碼如下：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int yeah(vector<vector<int>>& projects, int days);

int minDays(vector<vector<int>>& projects, int k) {
    int l = 0;
    int r = 0;

    for (auto project : projects) {
        r = max(r, project[0]);
    }

    int m, ans = r;

    while (l <= r) {
        m = (l + r) / 2;
        if (yeah(projects, m) <= k) {
            ans = m;
            r = m - 1;
        }
        else {
            l = m + 1;
        }
    }
    return ans;
}

int yeah(vector<vector<int>>& projects, int days) {
    int ans = 0;
    for (auto p : projects) {
        if (p[0] > days) {
            ans += (p[0] - days) * p[1];
        }
    }
    return ans;
}

int main() {
    vector<vector<int>> projects = { {1, 2}, {3, 4}, {5, 6} };
    int k = 4;

    int result = minDays(projects, k);

    cout << result << endl;

    return 0;
}

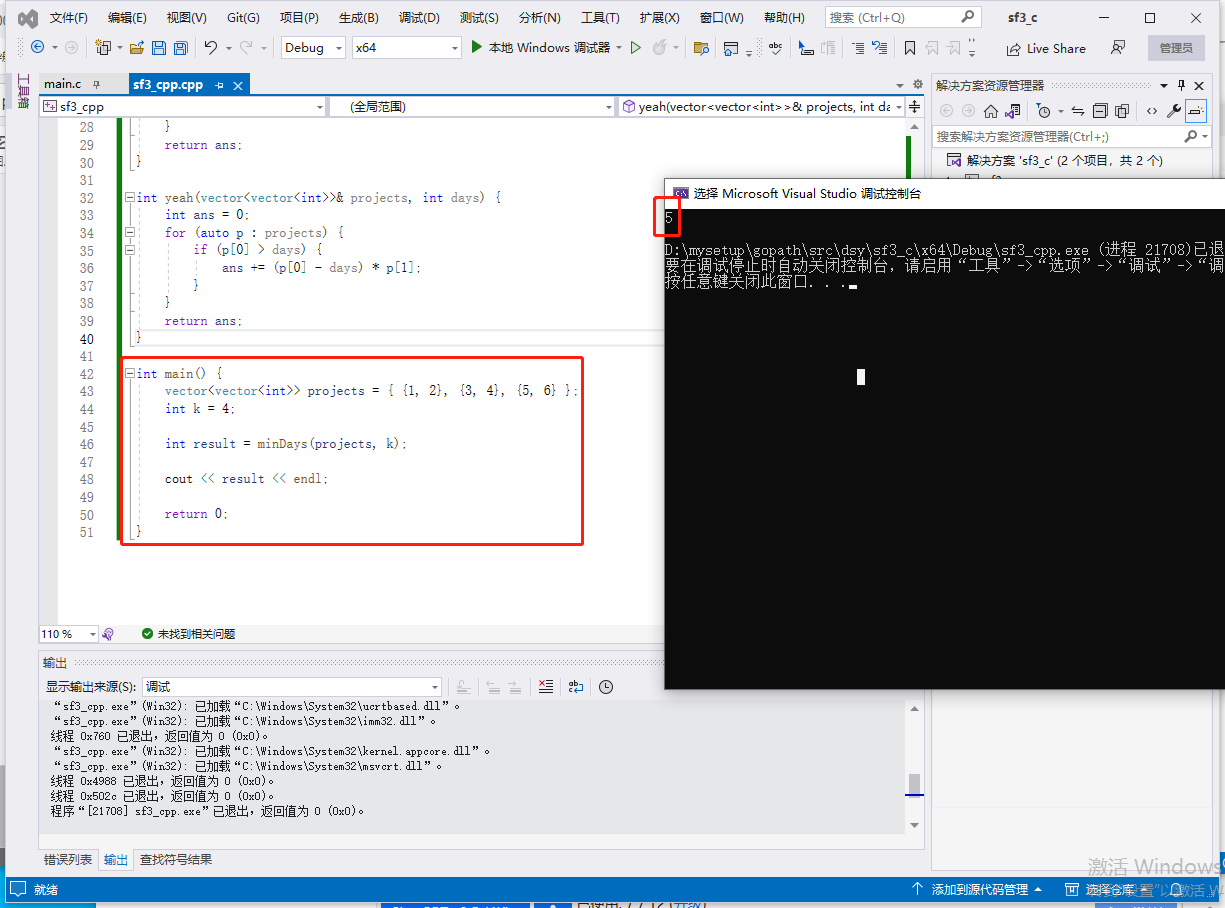
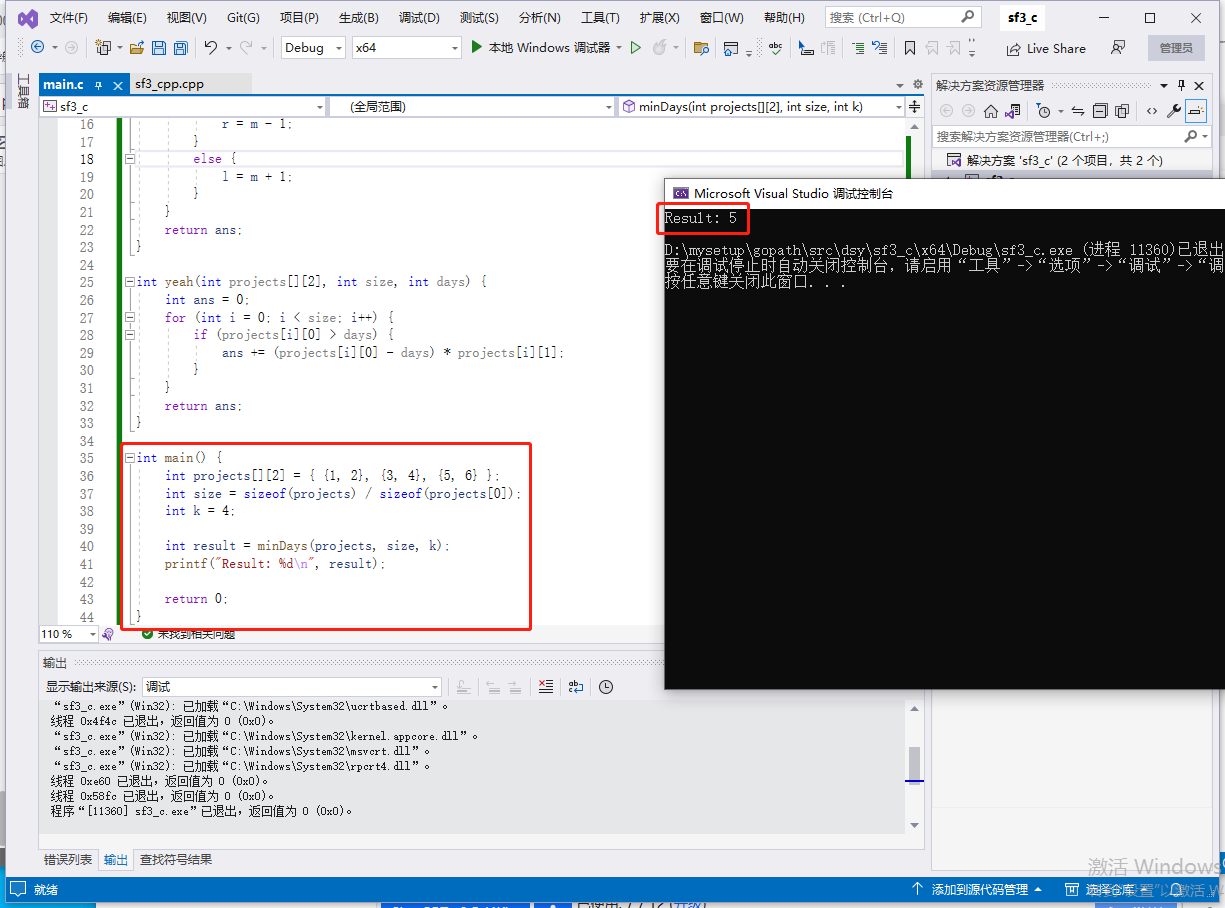
c完整程式碼如下：

#include <stdio.h>

int minDays(int projects[][2], int size, int k) {
    int l = 0;
    int r = 0;

    for (int i = 0; i < size; i++) {
        r = (projects[i][0] > r) ? projects[i][0] : r;
    }

    int m, ans = r;
    while (l <= r) {
        m = (l + r) / 2;
        if (yeah(projects, size, m) <= k) {
            ans = m;
            r = m - 1;
        }
        else {
            l = m + 1;
        }
    }
    return ans;
}

int yeah(int projects[][2], int size, int days) {
    int ans = 0;
    for (int i = 0; i < size; i++) {
        if (projects[i][0] > days) {
            ans += (projects[i][0] - days) * projects[i][1];
        }
    }
    return ans;
}

int main() {
    int projects[][2] = { {1, 2}, {3, 4}, {5, 6} };
    int size = sizeof(projects) / sizeof(projects[0]);
    int k = 4;

    int result = minDays(projects, size, k);
    printf("Result: %d\n", result);

    return 0;
}