小白也能看懂的 ROC 曲線詳解
作者:PrimiHub-Kevin
ROC 曲線是一種座標圖式的分析工具,是由二戰中的電子和雷達工程師發明的,發明之初是用來偵測敵軍飛機、船艦,後來被應用於醫學、生物學、犯罪心理學。
如今,ROC 曲線已經被廣泛應用於機器學習領域的模型評估,說到這裡就不得不提到 Tom Fawcett 大佬,他一直在致力於推廣 ROC 在機器學習領域的應用,他釋出的論文《An introduction to ROC analysis》更是被奉為 ROC 的經典之作(參照 2.2w 次),知名機器學習庫 scikit-learn 中的 ROC 演演算法就是參考此論文實現,可見其影響力!
不知道大多數人是否和我一樣,對於 ROC 曲線的理解只停留在呼叫 scikit-learn 庫的函數,對於它的背後原理和公式所知甚少。
前幾天我重讀了《An introduction to ROC analysis》終於將 ROC 曲線徹底搞清楚了,獨樂樂不如眾樂樂!如果你也對 ROC 的演演算法及實現感興趣,不妨花些時間看完全文,相信你一定會有所收穫!
一、什麼是 ROC 曲線
下圖中的藍色曲線就是 ROC 曲線,它常被用來評價二值分類器的優劣,即評估模型預測的準確度。
二值分類器,就是字面意思它會將資料分成兩個類別(正/負樣本)。例如:預測銀行使用者是否會違約、內容分為違規和不違規,以及廣告過濾、圖片分類等場景。篇幅關係這裡不做多分類 ROC 的講解。
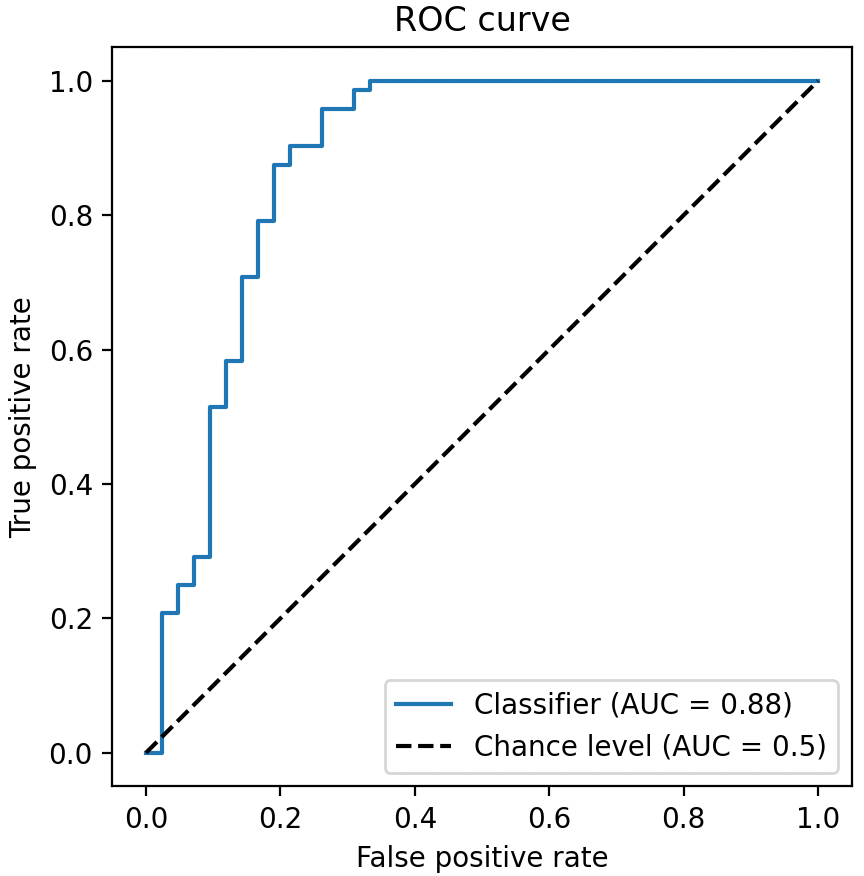
TPR: True positive rate; FPR: False positive rate
座標系中縱軸為 TPR(真陽率/命中率/召回率)最大值為 1,橫軸為 FPR(假陽率/誤判率)最大值為 1,虛線為基準線(最低標準),藍色的曲線就是 ROC 曲線。其中 ROC 曲線距離基準線越遠,則說明該模型的預測效果越好。
- ROC 曲線接近左上角:模型預測準確率很高
- ROC 曲線略高於基準線:模型預測準確率一般
- ROC 低於基準線:模型未達到最低標準,無法使用
二、背景知識
考慮一個二分類模型, 負樣本(Negative) 為 0,正樣本(Positive) 為 1。即:
- 標籤 \(y\) 的取值為 0 或 1。
- 模型預測的標籤為 \(\hat{y}\),取值也是 0 或 1。
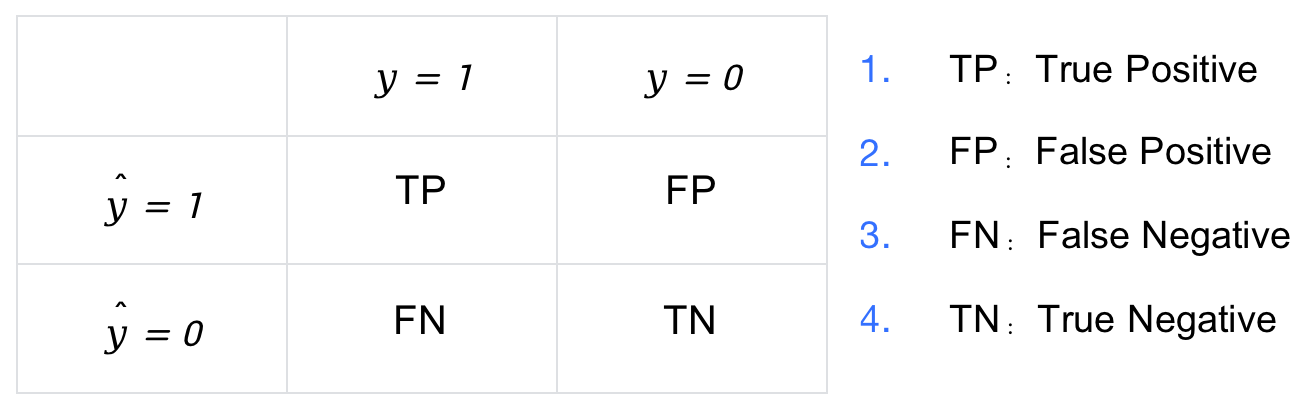
因此,將 \(y\) 與 \(\hat{y}\) 兩兩組合就會得到 4 種可能性,分別稱為:
2.1 公式
ROC 曲線的橫座標為 FPR(False Positive Rate),縱座標為 TPR(True Positive Rate)。FPR 統計了所有負樣本中 預測錯誤(FP) 的比例,TPR 統計了所有正樣本中 預測正確(TP) 的比例,其計算公式如下,其中 # 表示統計個數,例如 #N 表示負樣本的個數,#P 表示正樣本的個數
\(\text{FPR}=\frac{\#\text{FP}}{\#\text{N}}\),\(\text{TPR}=\frac{\#\text{TP}}{\#\text{P}}\)
2.2 計算方法
下面舉一個實際例子作為講解,以下表 5 個樣本為例,講解如何計算 FPR 和 TPR。
| id | 真實標籤\(y\) | 預測標籤\(\hat{y}\) |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 0 |
| 3 | 0 | 0 |
| 4 | 1 | 1 |
| 5 | 0 | 1 |
正樣本數 #P=3,負樣本數 #N=2。
其中 \(y=0\) 且 \(\hat{y}=1\) 的樣本有 1 個,即 #FP=1,所以 FPR=1/2=0.5
其中 \(y=1\) 且 \(\hat{y}=1\) 的樣本有 2 個,即 #TP=2,所以 FPR=2/3
FPR 和 TPR 的取值範圍均是 0 到 1 之間。對於 FPR,我們希望其越小越好。而對於 TPR,我們希望其越大越好。
至此,我們已經介紹完如何計算 FPR 和 TPR 的值,下面將會講解如何繪製 ROC 曲線。
三、繪製 ROC 曲線
講到這裡,可能有的同學會問:ROC 不是一條曲線嗎?講了這麼多它到底應該怎麼畫呢?下面將分為兩部分講解如何繪製 ROC 曲線,直接打通你的「任督二脈」徹底拿下 ROC 曲線:
- 第一部分:通過手繪的方式講解原理
- 第二部分:Python 程式碼實現,程式碼清爽易讀
如果說上面是「開胃小菜」,那下面就是正菜啦!
3.1 手繪 ROC 曲線
一般在二分類模型裡(標籤取值為 0 或 1),會預設設定一個閾值 (threshold)。當預測分數大於這個閾值時,輸出 1,反之輸出 0。我們可以通過調節這個閾值,改變模型預測的輸出,進而畫出 ROC 曲線。
以下面表格中的 20 個點為例,介紹如何人工畫出 ROC 曲線,其中正樣本和負樣本都是 10 個,即 #P = #N = 10。
| id | 真實標籤 | 預測分數 | id | 真實標籤 | 預測分數 |
|---|---|---|---|---|---|
| 1 | 1 | .9 | 11 | 1 | .4 |
| 2 | 1 | .8 | 12 | 0 | .39 |
| 3 | 0 | .7 | 13 | 1 | .38 |
| 4 | 1 | .6 | 14 | 0 | .37 |
| 5 | 1 | .55 | 15 | 0 | .36 |
| 6 | 1 | .54 | 16 | 0 | .35 |
| 7 | 0 | .53 | 17 | 1 | .34 |
| 8 | 0 | .52 | 18 | 0 | .33 |
| 9 | 1 | .51 | 19 | 1 | .30 |
| 10 | 0 | .505 | 20 | 0 | .1 |
當設定閾值為 0.9 時,只有第一個點預測為 1,其餘都為 0,故 #FP=0、#TP=1,計算出 FPR=0/10=0,TPR=1/10=0.1,畫出點 (0,0.1)
當設定閾值為 0.8 時,只有前兩個點預測為 1,其餘都為 0,故 #FP=0、#TP=2,計算出 FPR=0/10=0,TPR=2/10=0.2,畫出點 (0,0.2)
當設定閾值為 0.7 時,只有前三個點預測為 1,其餘都為 0,故 #FP=1、#TP=2,計算出 FPR=1/10=0.1,TPR=2/10=0.2,畫出點 (0.1,0.2)。
以此類推,畫出的 ROC 曲線如下:
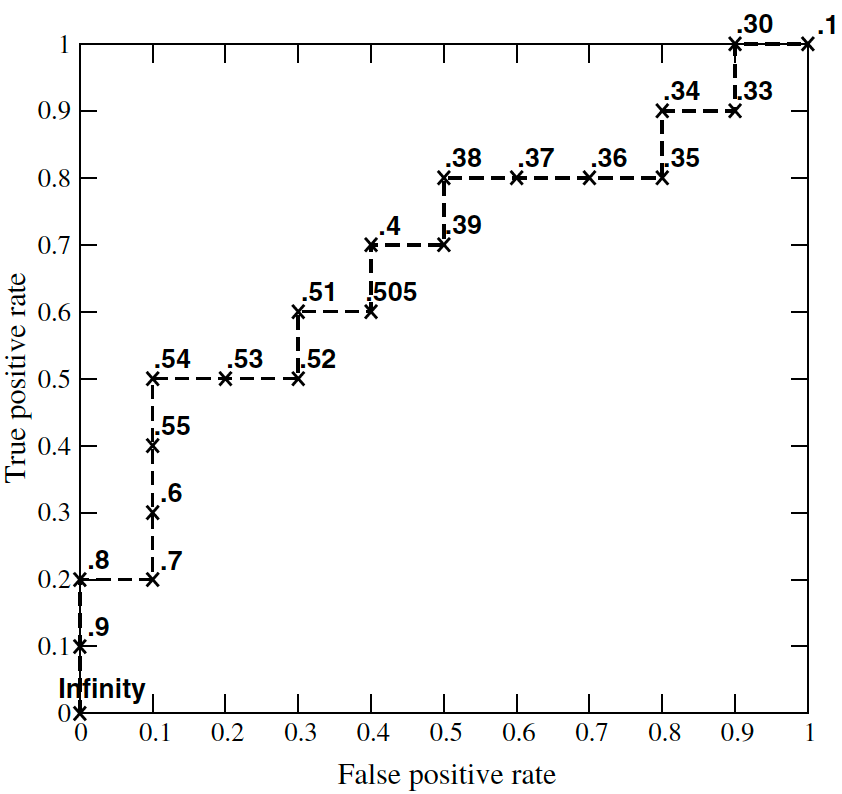
因此,在畫 ROC 曲線前,需要將預測分數從大到小排序,然後將預測分數依次設定為閾值,分別計算 FPR 和 TPR。而對於基準線,假設隨機預測為正樣本的概率為 \(x\),即 \(\Pr(\hat{y}=1)=x\) 由於 FPR 計算的是負樣本中,預測為正樣本的概率,因此 FPR=\(x\)(同理,TPR=\(x\))。所以,基準線為從點 (0, 0) 到 (1, 1) 的斜線。
3.2 Python 程式碼
接下來,我們將結合程式碼講解如何在 Python 中繪製 ROC 曲線。
下面的程式碼參考了《An Introduction to ROC Analysis》中的演演算法 1(虛擬碼)。值得一提的是,知名機器學習庫 scikit-learn 的 roc_curve 函數 也參考了這個演演算法。

下面我自己實現的 roc 函數可以理解為是簡化版的 roc_curve,這裡的程式碼邏輯更加簡潔易懂,演演算法的時間複雜度 \(O(n\log n)\)。完整的程式碼如下:
# import numpy as np
def roc(y_true, y_score, pos_label):
"""
y_true:真實標籤
y_score:模型預測分數
pos_label:正樣本標籤,如「1」
"""
# 統計正樣本和負樣本的個數
num_positive_examples = (y_true == pos_label).sum()
num_negtive_examples = len(y_true) - num_positive_examples
tp, fp = 0, 0
tpr, fpr, thresholds = [], [], []
score = max(y_score) + 1
# 根據排序後的預測分數分別計算fpr和tpr
for i in np.flip(np.argsort(y_score)):
# 處理樣本預測分數相同的情況
if y_score[i] != score:
fpr.append(fp / num_negtive_examples)
tpr.append(tp / num_positive_examples)
thresholds.append(score)
score = y_score[i]
if y_true[i] == pos_label:
tp += 1
else:
fp += 1
fpr.append(fp / num_negtive_examples)
tpr.append(tp / num_positive_examples)
thresholds.append(score)
return fpr, tpr, thresholds
匯入上面 3.1 表格中的資料,通過上面實現的 roc 方法,計算 ROC 曲線的座標值。
import numpy as np
y_true = np.array(
[1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0]
)
y_score = np.array([
.9, .8, .7, .6, .55, .54, .53, .52, .51, .505,
.4, .39, .38, .37, .36, .35, .34, .33, .3, .1
])
fpr, tpr, thresholds = roc(y_true, y_score, pos_label=1)
最後,通過 Matplotlib 將計算出的 ROC 曲線座標繪製成圖。
import matplotlib.pyplot as plt
plt.plot(fpr, tpr)
plt.axis("square")
plt.xlabel("False positive rate")
plt.ylabel("True positive rate")
plt.title("ROC curve")
plt.show()
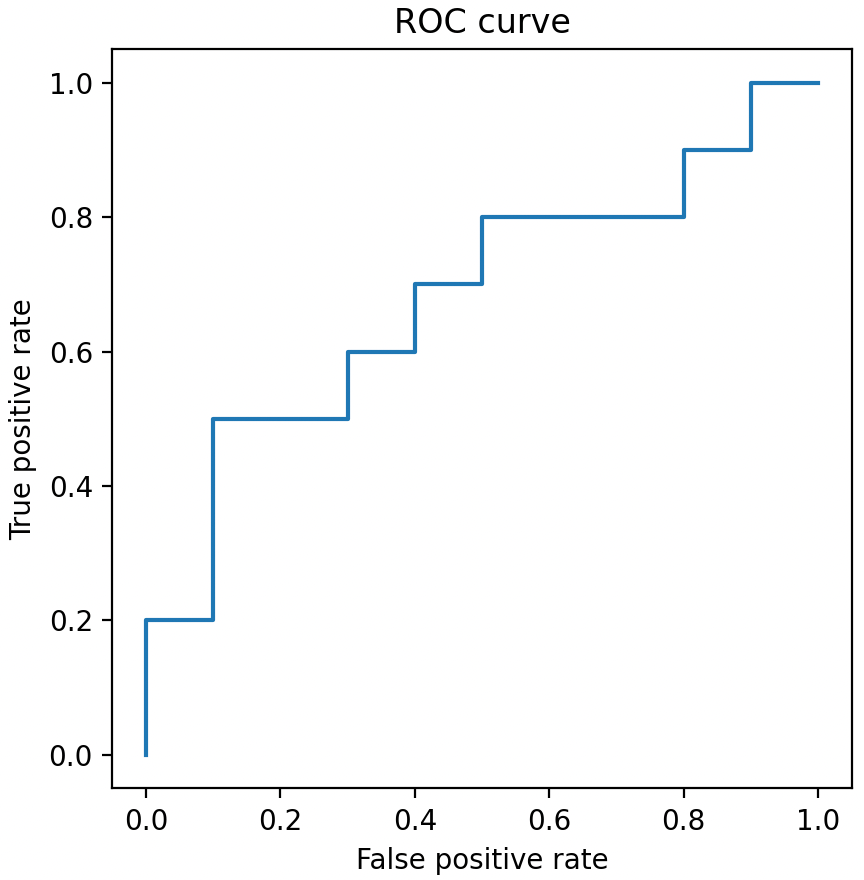
至此,ROC 的基礎知識部分就全部講完了,如果還想深入瞭解的同學可以繼續往下看。
四、聯邦學習中的 ROC 平均
如果將上面的內容比作「正餐」,那這裡就是妥妥乾貨了,打起精神衝鴨!
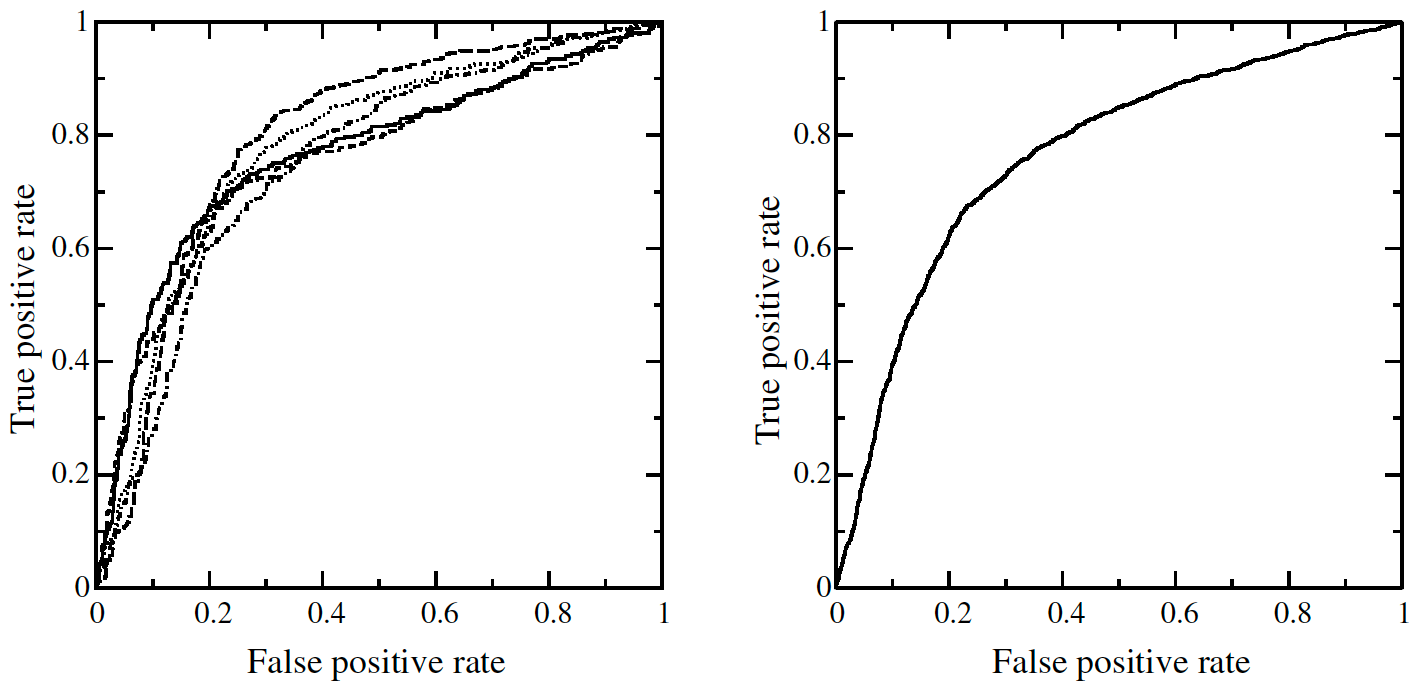
顧名思義,ROC 平均就是將多條 ROC 曲線「平均化」。那麼,什麼場景需要做 ROC 平均呢?例如:橫向聯邦學習中,由於樣本都在使用者本地,伺服器可以採用 ROC 平均的方式,計算近似的全域性 ROC 曲線。
ROC 的平均有兩種方法:垂直平均、閾值平均,下面將逐一進行講解,並給出 Python 程式碼實現。
4.1 垂直平均
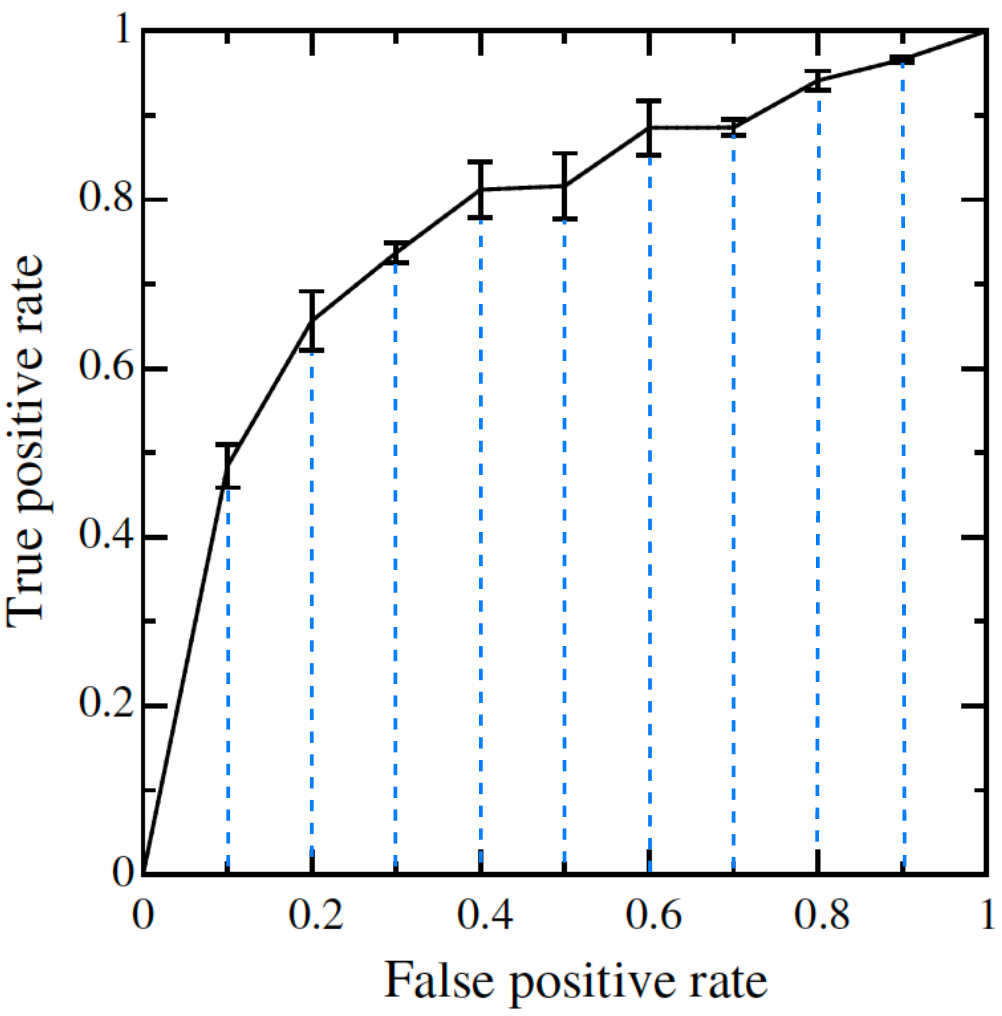
垂直平均(Vertical averaging)的思想是,選取一些 FPR 的點,計算其平均的 TPR 值。下面是論文中的演演算法描述的虛擬碼,看不懂可直接略過看 Python 程式碼實現部分。

下面是 Python 的程式碼實現:
# import numpy as np
def roc_vertical_avg(samples, FPR, TPR):
"""
samples:選取FPR點的個數
FPR:包含所有FPR的列表
TPR:包含所有TPR的列表
"""
nrocs = len(FPR)
tpravg = []
fpr = [i / samples for i in range(samples + 1)]
for fpr_sample in fpr:
tprsum = 0
# 將所有計算的tpr累加
for i in range(nrocs):
tprsum += tpr_for_fpr(fpr_sample, FPR[i], TPR[i])
# 計算平均的tpr
tpravg.append(tprsum / nrocs)
return fpr, tpravg
# 計算對應fpr的tpr
def tpr_for_fpr(fpr_sample, fpr, tpr):
i = 0
while i < len(fpr) - 1 and fpr[i + 1] <= fpr_sample:
i += 1
if fpr[i] == fpr_sample:
return tpr[i]
else:
return interpolate(fpr[i], tpr[i], fpr[i + 1], tpr[i + 1], fpr_sample)
# 插值
def interpolate(fprp1, tprp1, fprp2, tprp2, x):
slope = (tprp2 - tprp1) / (fprp2 - fprp1)
return tprp1 + slope * (x - fprp1)
4.2 閾值平均
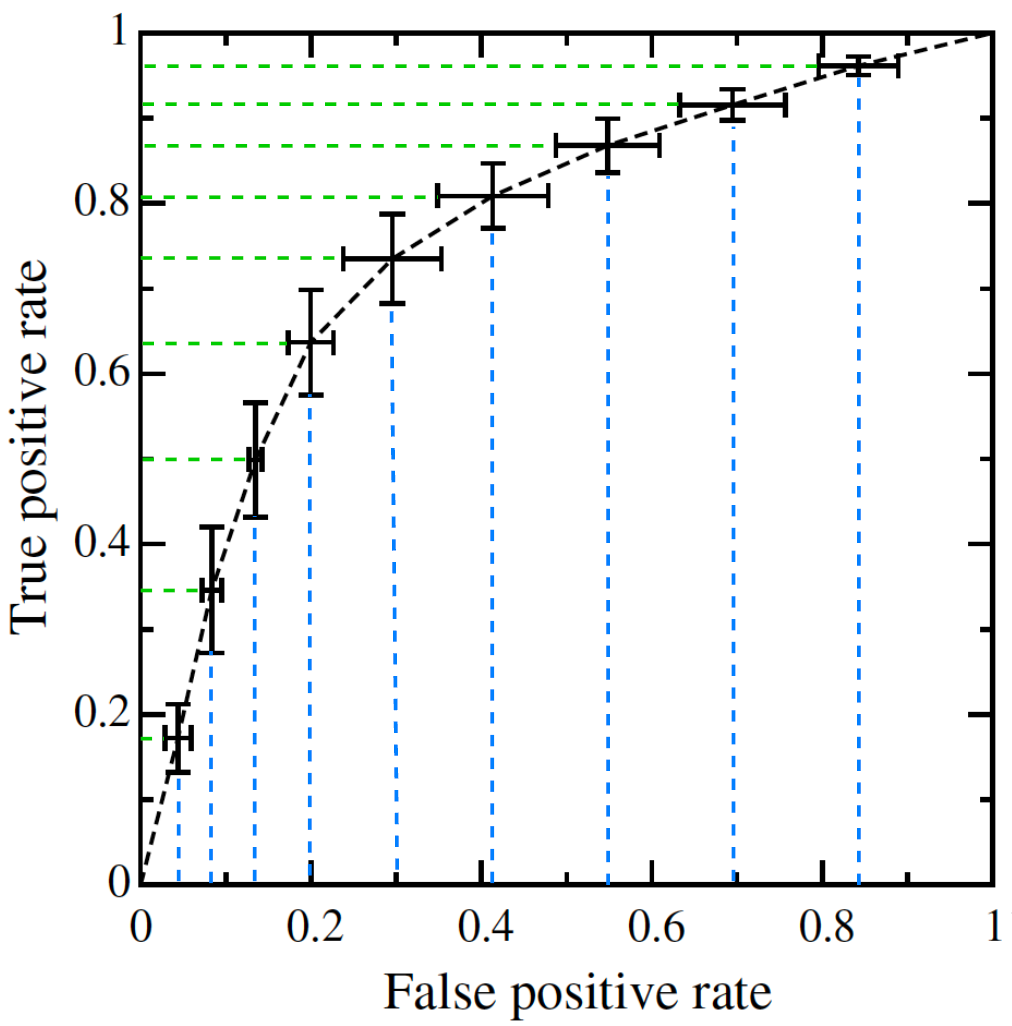
閾值平均(Threshold averaging)的思想是,選取一些閾值的點,計算其平均的 FPR 和 TPR。

下面是 Python 的程式碼實現:
# import numpy as np
def roc_threshold_avg(samples, FPR, TPR, THRESHOLDS):
"""
samples:選取FPR點的個數
FPR:包含所有FPR的列表
TPR:包含所有TPR的列表
THRESHOLDS:包含所有THRESHOLDS的列表
"""
nrocs = len(FPR)
T = []
fpravg = []
tpravg = []
for thresholds in THRESHOLDS:
for t in thresholds:
T.append(t)
T.sort(reverse=True)
for tidx in range(0, len(T), int(len(T) / samples)):
fprsum = 0
tprsum = 0
# 將所有計算的fpr和tpr累加
for i in range(nrocs):
fprp, tprp = roc_point_at_threshold(FPR[i], TPR[i], THRESHOLDS[i], T[tidx])
fprsum += fprp
tprsum += tprp
# 計算平均的fpr和tpr
fpravg.append(fprsum / nrocs)
tpravg.append(tprsum / nrocs)
return fpravg, tpravg
# 計算對應threshold的fpr和tpr
def roc_point_at_threshold(fpr, tpr, thresholds, thresh):
i = 0
while i < len(fpr) - 1 and thresholds[i] > thresh:
i += 1
return fpr[i], tpr[i]
在我們的 PrimiHub 聯邦學習模組中,就實現了上述 ROC 平均方法。
五、最後
本文由淺入深地詳細介紹了 ROC 曲線演演算法,包含演演算法原理、公式、計算、原始碼實現和講解,希望能夠幫助讀者一口氣(看的時候可得喘氣