技術文章 » BigCode 背後的大規模資料去重

BigCode 背後的大規模資料去重

2023-07-21 06:00:45

目標受眾

本文面向對大規模檔案去重感興趣，且對雜湊 (hashing) 、圖 (graph) 及文書處理有一定了解的讀者。

動機

老話說得好: 垃圾進，垃圾出 (garbage in, garbage out)，把資料處理乾淨再輸入給模型至關重要，至少對大語言模型如此。雖然現在一些明星大模型 (嚴格來講，它們很多是 API) 的存在讓大家恍惚產生了資料質量好像不那麼重要了的錯覺，但事實絕非如此。

在 BigScience 和 BigCode 專案中，在資料質量方面，我們面臨的一個很大的問題是資料重複，這不僅包括訓練集內的資料重複，還包括訓練集中包含測試基準中的資料從而造成了基準汙染 (benchmark contamination)。已經有研究表明，當訓練集中存在較多重複資料時，模型傾向於逐字輸出訓練資料 [1] (這一現象在其他一些領域並不常見 [2])，而且訓得的模型也更容易遭受隱私攻擊 [1]。除了能避免上面兩個問題外，去重還有不少好處:

  1. 讓訓練更高效: 你可以用更少的訓練步驟獲得相同的，甚至是更好的效能 [3] [4]。
  2. 防止可能的資料洩漏和基準汙染: 資料重複會損害你的模型效能報告的公信力，並可能讓所謂的改進淪為泡影。
  3. 提高資料可得性。我們大多數人都負擔不起重複下載或傳輸數千 GB 文字的成本，更不用說由此帶來的額外訓練成本了。對資料集進行去重，能使其更易於學習、傳輸及共同作業。

從 BigScience 到 BigCode

我想先分享一個故事，故事主要講述我如何接受資料去重這一任務，過程如何，以及在此過程中我學到了什麼。

一切開始於 LinkedIn 上的一次對話，當時 BigScience 已經開始幾個月了。Huu Nguyen 注意到我在 GitHub 上的一個小專案並找到了我，問我是否有興趣為 BigScience 做資料去重工作。我當然願意了，儘管當時我完全沒意識到由於資料量巨大，這項工作比想象中麻煩很多。

這項工作既有趣又充滿挑戰。挑戰在於，我對處理如此大規模的資料並沒有太多經驗。但專案組的每個人仍然歡迎我、信任我，還給了我數千美元的雲端計算預算。有多少回，我不得不從睡夢中醒來，反覆確認我是否關閉了那些雲範例。我不停地在試驗和錯誤中學習，在此過程中，新的視角被開啟了。如果沒有 BigScience，可能我永遠不會有這種視角。

一年後的今天，我正在把從 BigScience 學到的東西應用到 BigCode 專案中去，去處理更大的資料集。除了英語 [3] LLM 之外，我們已經再次證明資料去重也能改程序式碼模型 [4] 的效能。有了資料去重，我們可以用更小的資料集達到更優的效能。現在，親愛的讀者，我想與你分享我學到的知識，希望你能透過資料去重的鏡頭一瞥 BigCode 專案的幕後故事。

下表列出了 BigScience 專案中各資料集使用的去重方法，以供參考:

資料集 輸入資料量 輸出資料尺寸或資料精簡比 去重粒度 方法 引數 語種 耗時
OpenWebText2[5] 對 URL 去重後: 193.89 GB（69M） 使用 MinHash LSH 後: 65.86 GB（17M） URL + 檔案 URL（精確匹配）+ 檔案（MinHash LSH） \((10, 0.5, ?, ?, ?)\) 英語
Pile-CC[5] ~306 GB 227.12 GiB（~55M） 檔案 檔案（MinHash LSH） $(10, 0.5, ?, ?, ?) $ 英語 數天
BNE5[6] 2 TB 570 GB 檔案 Onion 5-元組 西班牙語
MassiveText[7] 0.001 TB ~ 2.1 TB 檔案 檔案（精確匹配 + MinHash LSH） \((?, 0.8, 13, ?, ?)\) 英語
CC100-XL[8] 0.01 GiB ~ 3324.45 GiB URL + 段落 URL（精確匹配） + 段落（精確匹配） SHA-1 多語種
C4[3] 806.92 GB (364M) 3.04% ~ 7.18% ↓ （訓練集） 子字串或檔案 子字串（字尾陣列）或檔案（MinHash） 字尾陣列：50-詞元，MinHash: \((9000, 0.8, 5, 20, 450)\) 英語
Real News[3] ~120 GiB 13.63% ~ 19.4% ↓（訓練集） 同 C4 同 C4 同 C4 英語
LM1B[3] ~4.40 GiB（30M） 0.76% ~ 4.86% ↓（訓練集） 同 C4 同 C4 同 C4 英語
WIKI40B[3] ~2.9M 0.39% ~ 2.76% ↓（訓練集） 同 C4 同 C4 同 C4 英語
BigScience ROOTS 語料集[9] 0.07% ~ 2.7% ↓ (檔案) + 10.61% ~ 32.30% ↓ (子字串) 檔案 + 子字串 檔案 (SimHash) + 子字串 (字尾陣列) SimHash：6-元組，漢明距離（hamming distance）為 4，字尾陣列：50-詞元 多語種 12 小時 ~ 數天

下表是我們在建立 BigCode 的訓練資料集 (訓練資料皆為程式碼) 時所用的方法。這裡，如果當遇到沒有名字的資料集時，我們就用模型名稱來代替。

模型 去重方法 引數 去重級別
InCoder[10] 精確匹配 程式碼詞元/MD5 + 布隆濾波（Bloom filtering） 檔案
CodeGen[11] 精確匹配 SHA256 檔案
AlphaCode[12] 精確匹配 忽略空格 檔案
PolyCode[13] 精確匹配 SHA256 檔案
PaLM Coder[14] Levenshtein 距離 檔案
CodeParrot[15] MinHash + LSH \((256, 0.8, 1)\) 檔案
The Stack[16] MinHash + LSH \((256, 0.7, 5)\) 檔案

MinHash + LSH 引數 \((P, T, K, B, R)\) :

  1. \(P\) 雜湊函數的個數或排列的個數
  2. \(T\) Jaccard 相似度閾值
  3. \(K\) K- 元組
  4. \(B\) 條帶數
  5. \(R\) 每條帶包含的行數

我們做了一個簡單的演示程式來說明這些引數對結果的影響: MinHash 數學演示。

例解 MinHash

在本節中，我們將詳細介紹在 BigCode 中使用的 MinHash 方法的每個步驟，並討論該方法的系統擴充套件性問題及其解決方案。我們以一個含有三個英文檔案為例來演示整個工作流程:

doc_id 內容
0 Deduplication is so much fun!
1 Deduplication is so much fun and easy!
2 I wish spider dog[17] is a thing.

MinHash 的典型工作流程如下:

  1. 詞袋生成 (生成 n- 元組) 及指紋生成 (生成 MinHash): 將每個檔案對映成一組雜湊值。
  2. 區域性敏感雜湊 (LSH): 逐條帶 (band) 的比較檔案的相似性，並將相似的檔案聚類以減少後續比較的次數。
  3. 去重: 決定保留或刪除哪些重複檔案。

詞袋生成

與大多數文字應用一樣，我們需要先把文字表示成詞袋，這裡我們通常使用 N- 元組詞袋。在本例中，我們使用以單詞為基本單元的 3- 元組 (即每 3 個連續單片語成一個元組)，且不考慮標點符號。我們後面會回過頭來討論元組大小對效能的影響。

doc_id 3-元組
0
1
2

這個操作的時間複雜度為 \(\mathcal{O}(NM)\)，其中 \(N\) 表示檔案數，而 \(M\) 表示檔案長度。也就是說，時間複雜度與資料集大小呈線性關係。我們可以用多程序或分散式計算來並行化詞袋生成過程。

指紋計算

使用 MinHash 方法時，每個 N- 元組需要生成多個雜湊值，此時我們通常要麼 1) 使用不同的雜湊函數進行多次雜湊，要麼 2) 使用一個雜湊函數進行雜湊後再進行多次重排。本例中，我們選擇第二種方法，重排生成 5 個雜湊值。 更多 MinHash 的變體可以參考 MinHash - 維基百科。

N-元組 雜湊值
Deduplication is so [403996643, 2764117407, 3550129378, 3548765886, 2353686061]
is so much [3594692244, 3595617149, 1564558780, 2888962350, 432993166]
so much fun [1556191985, 840529008, 1008110251, 3095214118, 3194813501]

對以上檔案雜湊矩陣中的每一列取最小值 —— 即 「MinHash」 中的 「Min」 的題中之義，我們就能得到該檔案最終的 MinHash 值:

doc_id MinHash
0 [403996643, 840529008, 1008110251, 2888962350, 432993166]
1 [403996643, 840529008, 1008110251, 1998729813, 432993166]
2 [166417565, 213933364, 1129612544, 1419614622, 1370935710]

從技術上講，雖然我們通常取最小值，但這並不代表我們一定要取每列的最小值。其他順序統計量也是可以的，例如最大值、第 k 個最小值或第 k 個最大值 [21]。

在具體實現時，我們可以使用 numpy 來對這些操作進行向量化。該操作的時間複雜度為 \(\mathcal{O}(NMK)\)，其中 \(K\) 是排列數。以下列出了我們的程式碼，它是基於 Datasketch 的實現修改而得的。

def embed_func(
    content: str,
    idx: int,
 *,
    num_perm: int,
    ngram_size: int,
    hashranges: List[Tuple[int, int]],
    permutations: np.ndarray,
) -> Dict[str, Any]:
    a, b = permutations
    masks: np.ndarray = np.full(shape=num_perm, dtype=np.uint64, fill_value=MAX_HASH)
    tokens: Set[str] = {" ".join(t) for t in ngrams(NON_ALPHA.split(content), ngram_size)}
    hashvalues: np.ndarray = np.array([sha1_hash(token.encode("utf-8")) for token in tokens], dtype=np.uint64)
    permuted_hashvalues = np.bitwise_and(
        ((hashvalues * np.tile(a, (len(hashvalues), 1)).T).T + b) % MERSENNE_PRIME, MAX_HASH
    )
    hashvalues = np.vstack([permuted_hashvalues, masks]).min(axis=0)
    Hs = [bytes(hashvalues[start:end].byteswap().data) for start, end in hashranges]
    return {"__signatures__": Hs, "__id__": idx}

熟悉 Datasketch 的讀者可能會問，為什麼我們要費心費力剝離 Datasketch 庫提供的所有高階功能？其主要原因並不是因為我們要減少依賴項，而是因為我們想要儘可能地榨取 CPU 的算力。而將多個步驟融合到一個函數中，是更好利用計算資源的手段之一。

由於每個檔案的計算互相獨立，因此我們可以充分利用 datasets 庫的 map 函數來實現並行化:

embedded = ds.map(
	function=embed_func,
	fn_kwargs={
		"num_perm": args.num_perm,
		"hashranges": HASH_RANGES,
		"ngram_size": args.ngram,
		"permutations": PERMUTATIONS,
	},
	input_columns=[args.column],
	remove_columns=ds.column_names,
	num_proc=os.cpu_count(),
	with_indices=True,
	desc="Fingerprinting...",
)

指紋計算完畢之後，每個檔案都被對映成了一個整數陣列。為了弄清楚哪些檔案彼此相似，我們需要根據這些指紋對它們進行聚類。輪到 區域性敏感雜湊 (Locality Sensitive Hashing，LSH) 閃亮登場了。

區域性敏感雜湊 (LSH)

LSH 將指紋陣列按行分成若干個條帶 (band)，每個條帶的行數相同，如果遇到最後一個條帶行數不足，我們就直接忽略它。以條帶數 \(b=2\) 為例，每個條帶有 \(r=2\) 行，具體組織如下:

doc_id MinHash 條帶
0 [403996643, 840529008, 1008110251, 2888962350, 432993166] [0:[403996643, 840529008], 1:[1008110251, 2888962350]]
1 [403996643, 840529008, 1008110251, 1998729813, 432993166] [0:[403996643, 840529008], 1:[1008110251, 1998729813]]
2 [166417565, 213933364, 1129612544, 1419614622, 1370935710] [0:[166417565, 213933364], 1:[1129612544, 1419614622]]

若兩個檔案在某條帶上 MinHash 值相同，這兩個檔案就會被聚到同一個桶中備選。

條帶 ID 條帶值 doc_ids
0 [403996643, 840529008] 0, 1
1 [1008110251, 2888962350] 0
1 [1008110251, 1998729813] 1
0 [166417565, 213933364] 2
1 [1129612544, 1419614622] 2

遍歷 doc_ids 列的每一行，將其中的檔案兩兩配對就生成了候選對。上表中，我們能生成一個候選對: (0, 1) 。

候選對生成後 ……

很多資料去重的論文或教學講完上一節就結束了，但在實際專案中我們還涉及如何處理這些候選對的問題。通常，候選對生成後，我們有兩個選擇:

  1. 由於 MinHash 只是一個近似，所以仍需計算兩個檔案的 N- 元組集合的交併比來算得準確的 Jaccard 相似性。此時，因為 LSH 已經幫我們過濾了不少，所以最終參與計算的候選對的量會大大減少。在 BigCode 專案中，我們起初就採用了這種做法，效果相當不錯。
  2. 我們還可以直接認可 LSH 選出來的相似對。這裡面可能會有個問題: Jaccard 相似性不具傳遞性，也就是說 \(A\) 相似於 \(B\) 且 \(B\) 相似於 \(C\)，並不意味著 \(A\) 相似於 \(C\)。所以這裡可能會有不少假陽性。通過在 The Stack 資料集上的實驗，我們發現，直接認可 LSH 選出來的相似對在很大程度上能提高下游模型的效能，同時還節省了處理時間和訓練時間。因此目前我們正慢慢開始轉向這種方法。但是，這個經驗並不是放之四海而皆準的，如果你準備在自己的資料集上仿效我們的做法，我們建議你在此之前好好檢查你的資料集及其特點，然後作出資料驅動的決策。

最後，我們可以用生成的相似文字對構建一個圖，在這個圖中，重複的檔案會被聚至同一個社群或同一個連通子圖中。不幸的是， datasets 在這方面幫不上什麼忙，因為現在我們需要類似 groupby 的功能，以根據 條帶 ID 及 檔案在該條帶上的取值 對檔案進行聚類。下面列出了我們嘗試過的一些方案:

方案 1: 老辦法，迭代資料集以建立圖，然後用一個圖處理庫對其做社群檢測或者連通分量檢測。

我們測試下來，該方案的擴充套件性不怎麼好，其原因是多方面的: 首先，整個資料集迭代起來很慢，而且記憶體消耗很大; 其次，諸如 graphtool 或 networkx 的市面上流行的圖處理庫建立圖的開銷較大。

方案 2: 使用流行的 Python 框架 (如 dask ) 及其高效的 groupby 操作。

但迭代慢和建立圖慢的問題仍然存在。

方案 3: 迭代資料集並使用並查集 (union find data structure) 對檔案進行聚類。

這個方案引入了一個很小的迭代開銷，對中等資料集的有不錯的效果不錯，但在巨量資料集上還是慢。

for table in tqdm(HASH_TABLES, dynamic_ncols=True, desc="Clustering..."):
	for cluster in table.values():
		if len(cluster) <= 1:
			continue
		idx = min(cluster)
		for x in cluster:
			uf.union(x, idx)

方案 4: 對巨量資料集，使用 Spark。

我們已經知道到 LSH 的有些步驟是可以並行化的，我們可以用 Spark 來實現它們。Spark 的好處是，它開箱即支援分散式 groupBy ，而且也能很輕鬆地實現像 [18] 這樣的連通分量檢測演演算法。注意，這裡我們並沒有使用 Spark 的原生 MinHash 實現，其原因是迄今為止我們所有的實驗都源於 Datasketch，而 Datasketch 的 MinHash 實現與 Spark 的原生實現完全不同。我們希望之前的經驗和教訓能幫助到後面的工作，而不是另起爐灶，進入另一個消融實驗的輪迴，因此我們選擇在 Spark 中自己實現 Datasketch 的 MinHash 演演算法。

edges = (
	records.flatMap(
		lambda x: generate_hash_values(
			content=x[1],
			idx=x[0],
			num_perm=args.num_perm,
			ngram_size=args.ngram_size,
			hashranges=HASH_RANGES,
			permutations=PERMUTATIONS,
		)
	)
	.groupBy(lambda x:(x[0], x[1]))
	.flatMap(lambda x: generate_edges([i[2] for i in x[1]]))
	.distinct()
	.cache()
)

以下是基於 [18] 的簡單連通分量檢測演演算法的 Spark 實現。

a = edges
while True:
	b = a.flatMap(large_star_map).groupByKey().flatMap(large_star_reduce).distinct().cache()
	a = b.map(small_star_map).groupByKey().flatMap(small_star_reduce).distinct().cache()
	changes = a.subtract(b).union(b.subtract(a)).collect()
	if len(changes) == 0:
		break

results = a.collect()

多虧了雲端計算提供商，我們可以使用 GCP DataProc 等服務輕鬆地搭建 一個 Spark 叢集。 最終，我們把程式執行起來，只用了不到 4 小時就完成了 1.4 TB 資料的去重工作，每小時僅需 15 美元。

資料質量很重要

我們不可能爬著梯子登上月球。因此我們不僅要確保方向正確，還要確保方法正確。

早期，我們使用的引數主要來自 CodeParrot 的實驗，消融實驗表明這些引數確實提高了模型的下游效能 [16]。後來，我們開始沿著這條路進一步探索，由此進一步確認了以下結論 [4]:

  1. 資料去重可以在縮小資料集 (6 TB VS. 3 TB) 規模的同時提高模型的下游效能
  2. 雖然我們還沒有完全搞清楚其能力邊界及限制條件，但我們確實發現更激進的資料去重 (6 TB VS. 2.4 TB) 可以進一步提高效能，方法有:
  3. 降低相似度閾值
  4. 使用更長的元組 (如: 一元組 → 五元組)
  5. 放棄誤報檢查，承受一小部分誤報帶來的資料損失

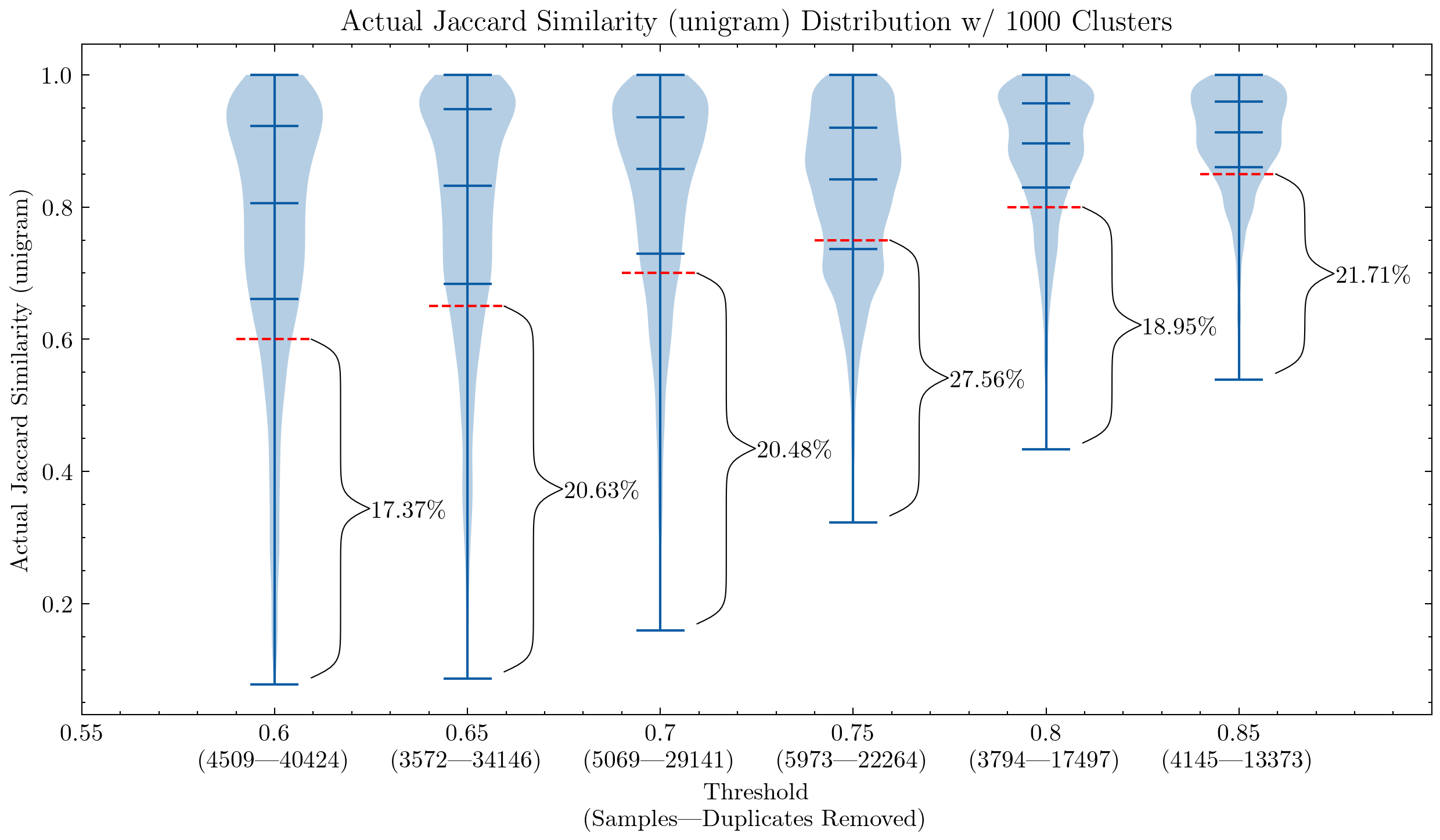
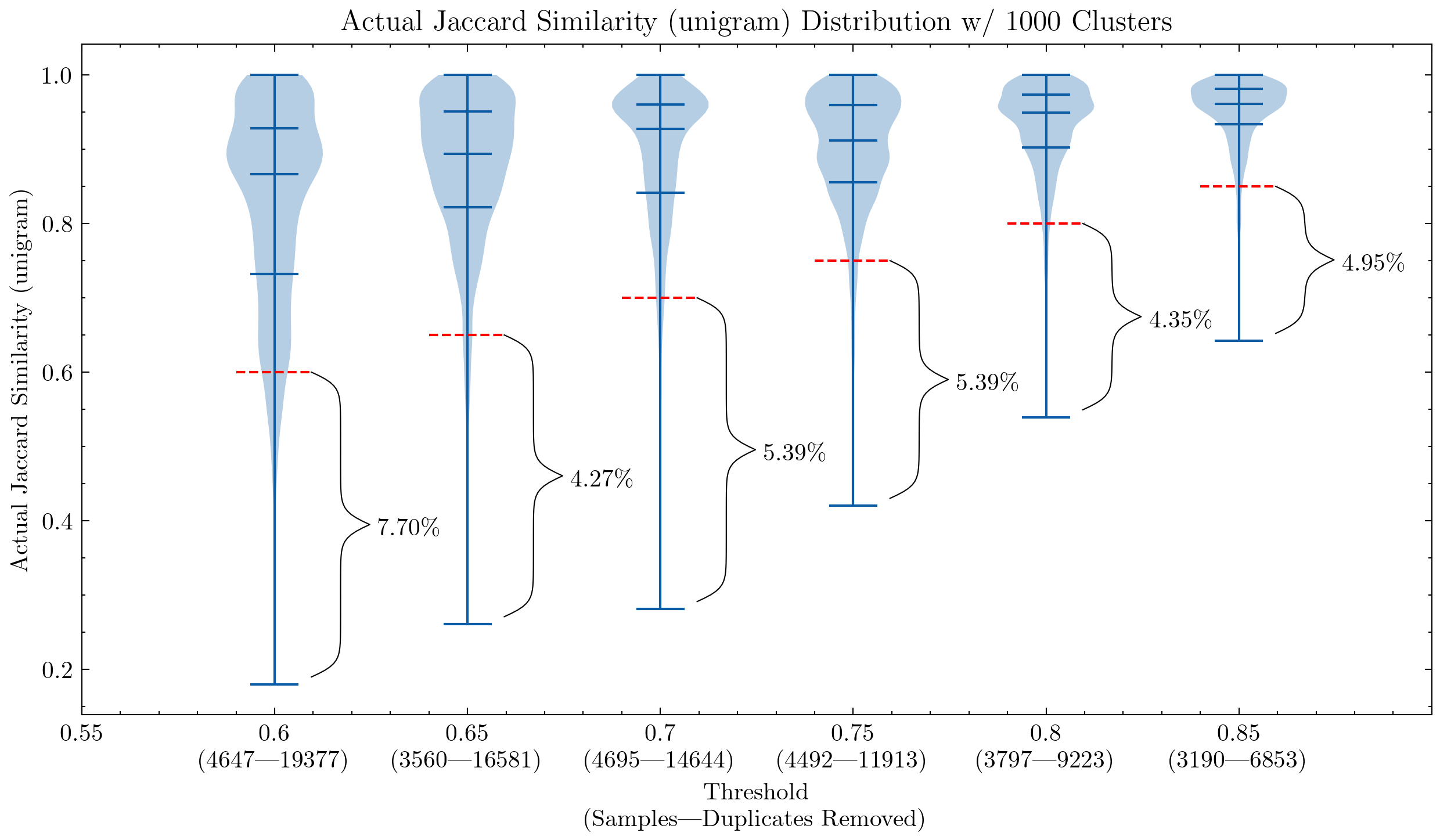
圖例: 上述兩幅圖展示了相似性閾值和元組大小帶來的影響，第一幅圖使用 1- 元組，第二幅圖使用 5- 元組。紅色虛線表示相似性閾值: 低於該值的檔案與同一簇中其他檔案的相似性低於閾值，我們將其視為誤報。

上面兩幅圖可以幫助我們理解為什麼有必要仔細檢查 CodeParrot 以及早期版本的 The Stack 訓練資料上的誤報: 這是使用 1- 元組的誤報比例會很大; 上圖還表明，將元組大小增加到 5，誤報比例會顯著降低。如果想激進點去重的話，閾值可以設低點。

還有實驗表明，降低閾值會刪除更多包含部分相似內容的檔案，因此意味著提高了我們最想刪除的那部分檔案的查全率。

系統擴充套件性

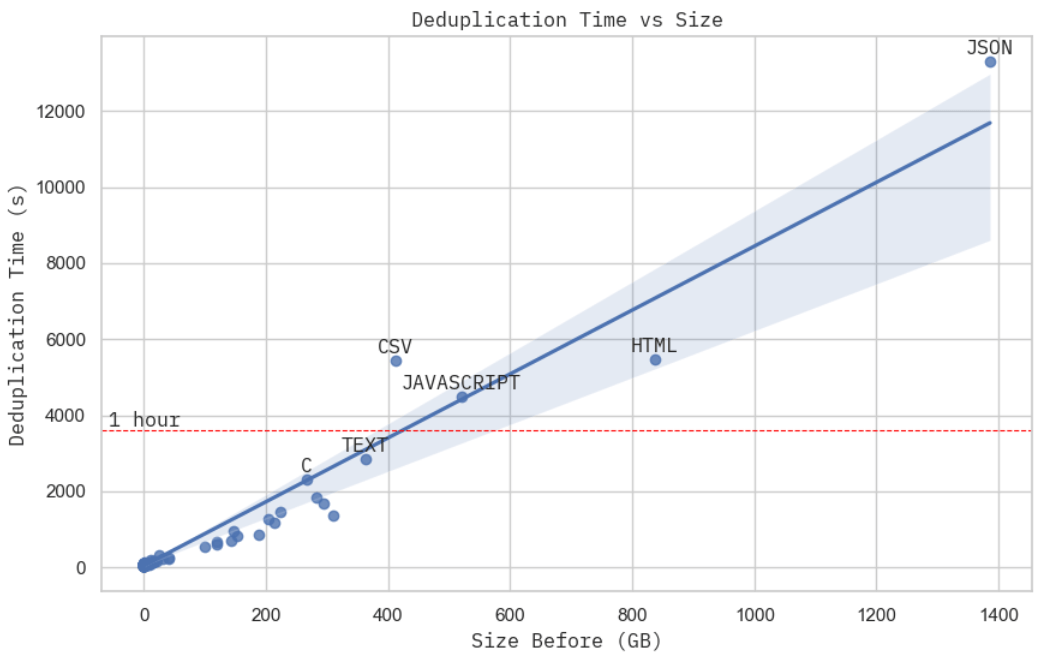
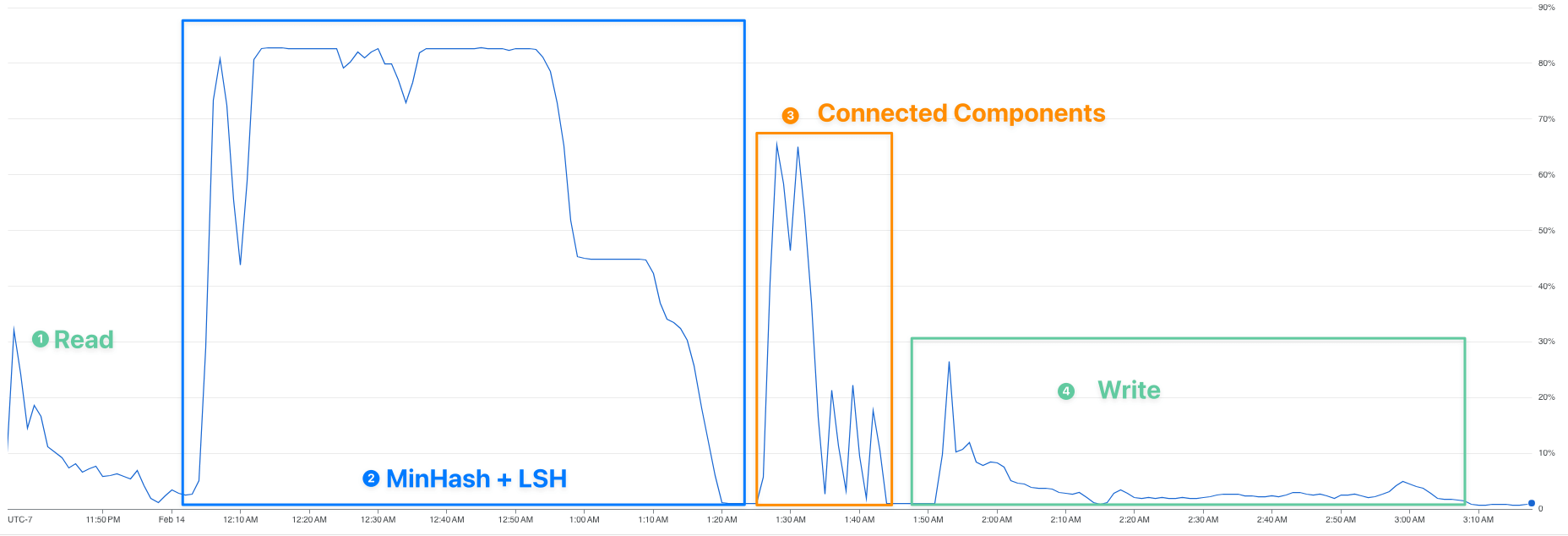
圖例: 資料去重時間與原始資料集規模的關係。測試基於 GCP 上的 15 個 c2d-standard-16 範例，每個範例每小時的成本約為 0.7 美元。

圖例: 叢集在處理 JSON 資料集時的 CPU 使用率。

上述擴充套件性資料未必非常嚴格，但也足夠說明，在給定預算的情況下，資料去重耗時與資料集規模的關係應該是線性的。如果你仔細看一下處理 JSON 資料集 (The Stack 資料集的最大子集) 的叢集資源使用情況，你會發現實際總計算時間 (圖中第 2 和第 3 階段) 主要都花在了 MinHash + LSH (圖中第 2 階段) 上，這與我們先前的分析一致，即第 2 階段 d 的時間複雜度為 $ \mathcal{O}(NM) $ — 與資料體量成線性關係。

謹慎行事

資料去完重並不意味著萬事大吉了，你仍然需要對資料進行徹底的探索和分析。此外，上文這些有關資料去重的發現來自於 The Stack 資料集，並不意味著它能無腦適用於其他資料集或語言。要構建一個好的訓練資料集，我們僅僅邁出了萬里長征的第一步，後面還有很多工作要做，例如資料質量過濾 (如過濾漏洞資料、毒性資料、偏見資料、模板生成的資料、個人身份資料等)。

我們還鼓勵你在訓練前像我們一樣對資料集進行徹底的分析，因為大家的情況可能各不相同。例如，如果你的時間和計算預算都很緊張，那麼資料去重可能不是很有幫助: @geiping_2022 提到基於子字串的資料去重並沒有提高他們模型的下游效能。在使用前，可能還需要對現存資料集進行徹底檢查，例如，@gao_2020 宣告他們只確保 Pile 本身及其子集都已去重，但不保證其與任何下游基準資料集沒有重複，要不要對 Pile 與下游基準資料集進行去重取決於使用者自己。

在資料洩露和基準汙染方面，還有很多需要探索的地方。由於 HumanEval 也是 GitHub Python 儲存庫之一，我們不得不重新訓練了我們的程式碼模型。早期的工作還發現，最流行的編碼基準之一的 MBPP[19] 與許多 Leetcode 問題有很多相似之處 (例如，MBPP 中的任務 601 基本上是 Leetcode 646，任務 604 ≃ Leetcode 151)。我們都知道 GitHub 中不乏很多程式設計挑戰賽題及其答案程式碼。如果居心叵測的人把所有基準測試的 Python 程式碼以不易察覺的方式上傳到 Github，汙染你所有的訓練資料，這事兒就更難了。

後續方向

  1. 子串去重。儘管在英語 [3] 上子串去重是有益的，但尚不清楚是否對程式碼資料也有用;
  2. 重複段落: 在一篇檔案中重複多次的段落。 @rae_2021 分享了一些關於如何檢測和刪除它們的有趣的啟發式方法。
  3. 使用模型嵌入進行語意級的去重。這是另外一套思路了，需要一整套去重、擴充套件性、成本、銷蝕等各方面的實驗和權衡。對此 [20] 提出了一些有趣的看法，但我們仍然需要更多實際證據才能得出結論 (其文字去重工作僅參考了 @lee_2022a 的工作，而 @lee_2022a 的主張主要是去重有作用而並未證明其效果達到了 SOTA)。
  4. 優化。還有不少優化空間: 更好的質量評估標準、擴充套件性、對下游效能影響的分析等。
  5. 換個角度: 對相似資料，去重到什麼程度就會開始損害效能？需要保留多少相似資料以保留資料的多樣性又不至冗餘？

致謝

題圖中的表情符 (Hugging Face、聖誕老人、檔案、巫師以及魔杖) 來自於 Noto Emoji (Apache 2.0)。我也莊嚴保證，這篇博文是我一個字一個字敲出來的，沒有使用任何文字生成 API。

非常感謝 Huu Nguyen(@Huu) 和 Hugo Laurençon(@HugoLaurencon) 在 BigScience 專案中的合作，以及 BigCode 專案中每個人一路上的幫助！如果你發現任何錯誤，請隨時聯絡我: mouchenghao at gmail dot com。

更多資源

參考文獻

英文原文: https://huggingface.co/blog/dedup

原文作者: Chenghao Mou

譯者: Matrix Yao (姚偉峰)，英特爾深度學習工程師，工作方向為 transformer-family 模型在各模態資料上的應用及大規模模型的訓練推理。

審校/排版: zhongdongy (阿東)