折積操作

一、torch.nn中Convolution Layers函數的介紹

1. 引數介紹

• nn.Conv1d: Conv取自Convolution的前四個字母，1d代表的是一個一維操作。

• nn.Conv2d: 2d表示是一個二維的操作，比如影象就是一個二維的。

• 其餘引數不常用，見官網檔案：torch.nn — PyTorch 2.0 documentation

2. torch.nn和torch.nn.functional的區別

• torch.nn是對torch.nn.functional的一個封裝，讓使用torch.nn.functional裡面的包的時候更加方便

• torch.nn包含了torch.nn.functional，打個比方，torch.nn.functional相當於開車的時候齒輪的運轉，torch.nn相當於把車裡的齒輪都封裝好了，為我們提供一個方向盤

• 如果只是簡單應用，會torch.nn就好了。但要細緻瞭解折積操作，需要深入瞭解torch.nn.functional

• 開啟torch.nn.functional的官方檔案，可以看到許多跟折積相關的操作：torch.nn.functional — PyTorch 2.0 documentation

二、torch.nn.functional.conv2d 介紹

官網檔案：torch.nn.functional.conv2d — PyTorch 2.0 documentation

torch.nn.functional.conv2d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1)

1. 引數詳解

• input: 輸入，資料型別為tensor，形狀尺寸規定為：(minibatch, 幾個通道(in_channels), 高, 寬)

• weight: 權重。更專業地來說可以叫折積核，形狀尺寸規定為：(輸出的通道(out_channel), \(in\_channel\over{groups}\)(groups一般取1), 高, 寬 )

• bias: 偏置。

• strids: 步幅。

• padding: 填充。

2. 舉例講解引數strids

（1）理論

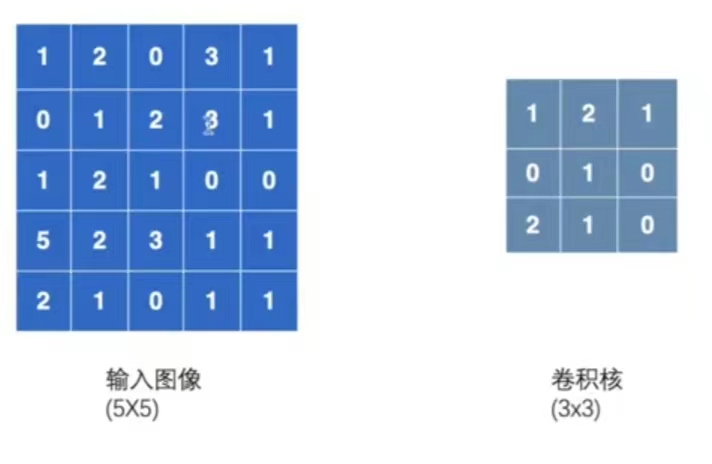
輸入一個5×5的影象，其中的數位代表在每個畫素中的顏色顯示。折積核設定為3×3的大小。

• strids引數的輸入格式是單個數或者形式為 (sH,sW) 的元組，可以理解成：比如輸入單個數：strids=1，每次折積核在影象中向上下或左右移1位；如果輸入strids=(2,3)，那麼每次折積核在影象中左右移動（橫向移動）時，是移動2位，在影象中上下移動（縱向移動）時，是移動3位。

• 本例設定strids=1

第一次移位：

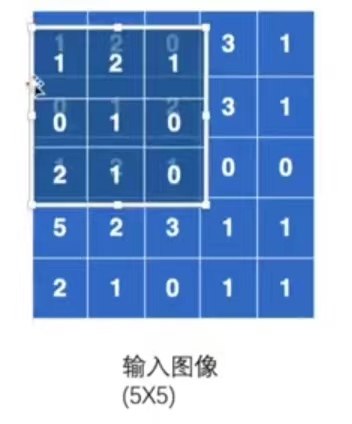
• 基於上述的假設，在做折積的過程中，需要將折積核將影象的前三行和前三列進行匹配：
  

• 在匹配過後，進行折積計算：對應位相乘然後相加，即

  \[1×1+2×2+0×1+0×0+1×1+2×0+1×2+2×1+1×0=10 \]

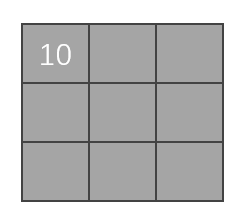
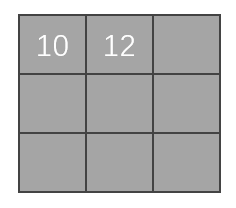
• 上面的得出的\(10\)可以賦值給矩陣，然後作為一個輸出
  

• 之後折積核可以在影象中進行一個移位，可以向旁邊走1位或2位，如下圖（向右走2位）。具體走多少位由strids引數決定，比如strids=2，那就是走2位。本例設定stride=1。
  

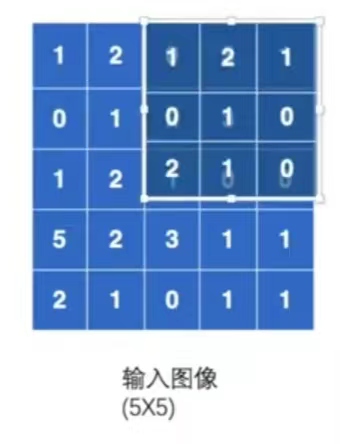
第二次移位：

• 向右移動一位，進行折積計算：

  \[2×1+0×2+3×1+1×0+2×1+3×0+2×2+1×1+0×0=12 \]

• \(12\)可以賦值給矩陣，然後作為一個輸出
  

第三次移位：

• 向右移動一位，進行折積計算：

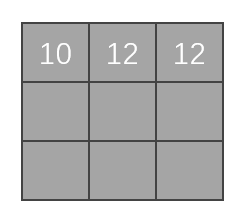
  \[0×1+3×2+1×1+2×0+3×1+1×0+1×2+0×1+0×0=12 \]

• \(12\)可以賦值給矩陣，然後作為一個輸出
  

• 第三次移位後，發現折積核已經沒辦法向右移位，進行匹配了。所以我們在縱向上，向下走：
  

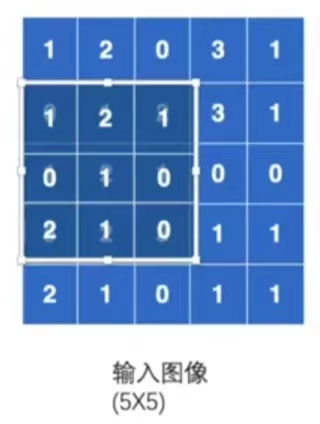
第四次移位：

• 在最開始的位置上，向下移動一位，進行折積計算：

  \[0×1+1×2+2×1+1×0+2×1+1×0+5×2+2×1+2×0=18 \]

• \(18\)可以賦值給矩陣，然後作為一個輸出
  

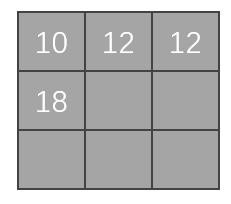
第五次移位：

• 在上面的基礎上，向右移一位，進行折積計算：

  \[1×1+2×2+3×1+2×0+1×1+0×0+2×2+3×1+1×0=16 \]

• \(16\)可以賦值給矩陣，然後作為一個輸出
  

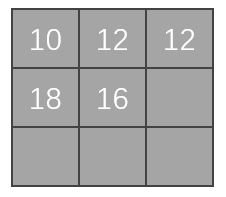
以此類推，走完整個影象，最後輸出的矩陣如下圖。這個矩陣是折積後的輸出。

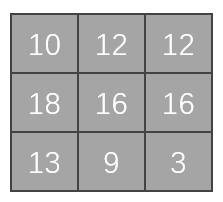
（2）程式操作

將上面的過程寫到程式內：

import torch
import torch.nn.functional as F

# 構造輸入影象（input引數輸入的資料型別為tensor,並且為2維）
input=torch.tensor([[1,2,0,3,1],
                    [0,1,2,3,1],
                    [1,2,1,0,0],
                    [5,2,3,1,1],
                    [2,1,0,1,1]])

# 構造折積核（資料型別也是tensor，並且為2維）
kernel=torch.tensor([[1,2,1],
                     [0,1,0],
                     [2,1,0]])

#檢視尺寸,輸出後發現並不符合引數輸入的尺寸標準，所以需要進一步轉換資料
print(input.shape) #[Run]  torch.Size([5, 5])
print(kernel.shape) #[Run]  torch.Size([3, 3])

#轉換input、kernel資料
input=torch.reshape(input,(1,1,5,5))  #torch.reshape(tensor資料,想變成的格式尺寸(batch=1,通道=1,5×5))
kernel=torch.reshape(kernel,(1,1,3,3))

#檢視尺寸,輸出後發現符合引數輸入的尺寸標準
print(input.shape) #[Run]  torch.Size([1, 1, 5, 5])
print(kernel.shape) #[Run]  torch.Size([1, 1, 3, 3])

# 進行折積操作
#stride=1,輸出結果與上面矩陣一致
output=F.conv2d(input,kernel,stride=1)
print(output)
"""
[Run]
tensor([[[[10, 12, 12],
          [18, 16, 16],
          [13,  9,  3]]]])
"""

#stride=2
output2=F.conv2d(input,kernel,stride=2)
print(output2)
"""
[Run]
tensor([[[[10, 12],
          [13,  3]]]])
"""

3. 舉例講解引數padding

padding的作用是在輸入影象的左右兩邊進行填充，padding的值決定填充的大小有多大，它的輸入形式為一個整數或者一個元組 ( padH, padW )，其中，padH=高，padW=寬。預設padding=0，即不進行填充。

（1）理論

• 仍輸入上述的5×5的影象，並設定padding=1，那麼輸入影象將會變成下圖，即影象的上下左右都會拓展一個畫素，然後這些空的地方畫素（裡面填充的資料）都預設為0。
  

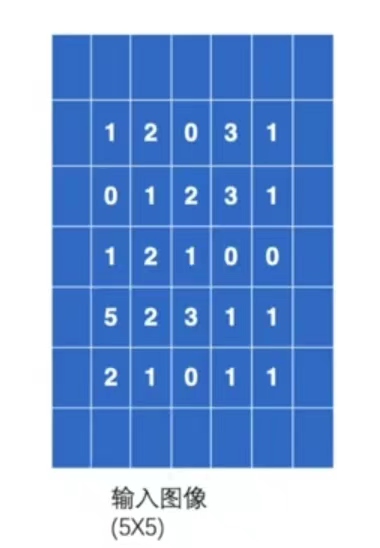
• 按上面的順序進行折積計算，第一次移位時在左上角3×3的位置，折積計算公式變為：

  \[0×1+0×2+0×1+0×0+1×1+2×0+0×2+0×1+1×0=1 \]

• 以此類推，完成後面的折積計算，並輸出矩陣

（2）程式操作

在上面的程式碼後，加入這串程式碼，以驗證padding的操作：

output3=F.conv2d(input,kernel,stride=1,padding=1)
print(output3)
"""
[Run]
tensor([[[[ 1,  3,  4, 10,  8],
          [ 5, 10, 12, 12,  6],
          [ 7, 18, 16, 16,  8],
          [11, 13,  9,  3,  4],
          [14, 13,  9,  7,  4]]]])
"""