簡單瞭解下最近正火的SwissTable
去年看到位元組跳動給golang提了issue建議把map的底層實現改成SwissTable的時候,我就有想寫這篇部落格了,不過因為種種原因一直拖著。
直到最近遇golang官方開始討論為了是否要接受SwissTable作為map的預設實現,以及實際遇到了一個hashtable有關的問題,促使我重新思考了常見的hashtable演演算法,並決定寫下這篇文章。
友情提示:本文不會從零教你寫hashtable或者swisstable,並且需要你對hashtable有一點了解(至少用過且知道常用操作的時間複雜度);文中給出的範例程式碼為了簡單易懂,放棄了一些實現細節上的優化,所以會和一些現成的實現不一樣,還請注意。
接下來我們先簡單複習下hashtable,雜湊表。
傳統的雜湊表
雜湊表提供了一個key到對應value的對映,通過一個hash函數把key轉換成某個「位置「,從這個位置上可以直接拿到我們想要的value,這就是雜湊表的能力。
雜湊表一般來說空間複雜度為O(n),查詢、插入、刪除的平均時間複雜度是O(1),最壞情況均為O(n)。
可見雜湊表在理論上是個效能非常好的資料結構。事實上在大多數情況下也確實是這樣。
在更進一步探討之前,我們先要假設幾個前提。
- 假設相同的資料作為key時計算出的hash結果總是一模一樣的;而資料不同時(哪怕只有一個bit不同時)計算出的hash結果也會完全不同。
根據鴿巢原理,上述假設在真實世界裡是不成立的,不過一般hash函數可產生的hash值的數量很大,通常比較難遇到不同資料產生相同hash的情況,所以這裡我們暫且讓這條假設成立。
- 對於hash函數產生的hash值,每一個bit都是隨機的,且隨機概率均等。
這條假設確保了不會有某些bit會有固定值或者某些值的權重比另一些高導致不平衡,工業級強度的hash函數一般都會盡量保證這條假設裡提出的要求。
符合以上兩條的我們認為它是一個「理想的hash函數」,這樣的函數可以最高效的利用hashtable的記憶體並減少衝突。換句話說,有了這樣的函數的話影響傳統hashtable效能的就只有資料在記憶體中的組織方式了。這樣也方便我們接下來的討論。
不過hash函數再完美,把key對映到一個有限大小的記憶體空間內也還是不可避免得會產生衝突:兩個不同的key會被對映到同一個位置。
為了解決這個問題,傳統的hashtable有好幾個解決方案,我們挑最常見的解決衝突的辦法——「連結串列法」和「線性探測法」簡單複習一下。
連結串列法
連結串列法是最常見的,它的中心思想在於如果key對映到了相同的位置,那麼就把這些key和value存在一張連結串列裡。
查詢的時候先用hash函數計算得到位置,然後再從存放在該位置上的連結串列裡一個個遍歷找到key相等的條目。
它的結構類似這樣:
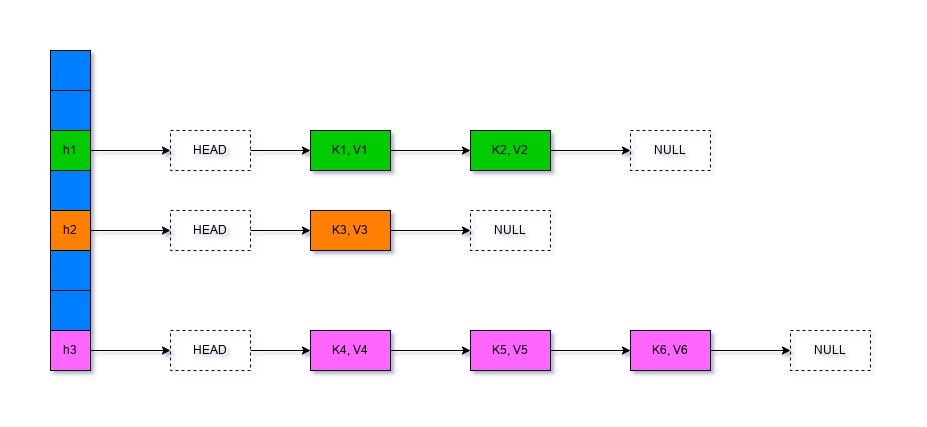
淡藍色的表示還沒有元素存在。
這個是最原始的實現方式,實際上很多庫不會每個位置(以後簡稱為slot)存一個連結串列,而是用一張大連結串列把每個有值存在的slot串聯起來,這樣可以節約n-1個頭結點和n-1個為節點的記憶體。
還有一些庫會在連結串列過長的時候把它轉換成搜尋樹等時間複雜度更低的結構。所以總體來看拉鍊法實現的雜湊表常用操作的平均時間複雜度都接近於O(1)。
優點:
- 實現很簡單,沒那麼多邊界條件要考慮
- 插入資料和刪除資料很快,插入用連結串列的頭插法,刪除只需要移動部分節點的next指標
- 能採取擴容之外的手段阻止查詢效能退化,比如前面提到的把過長連結串列轉換成搜尋樹
- 保證了指標穩定性,所以可以放心地用指標去參照雜湊表內的元素
缺點:
- 連結串列本身對快取不夠友好,衝突較多的時候快取命中率較低從而影響效能。
- 不同的slot之間資料在記憶體裡的跨度較大(即使是用大連結串列串聯的情況下),資料結構整體的空間區域性性較差
設計上的注意點:
- 為什麼不同雙連結串列?因為單連結串列夠用了操作是有點麻煩還需額外的頭節點,但雙連結串列每個節點都會比單連結串列多出一個指標,會浪費比一個頭結點更多的記憶體。
- 為什麼不直接用vector?因為刪除元素的時候vector需要移動大量元素,效能和指標穩定性上都得不到保證,不實用。
線性探測法
線性探測是另一種常見的雜湊表衝突解決方法。
它解決衝突的方式於連結串列法不同,在遇到hash衝突的時候,它會從衝突的位置開始向後一個個查詢,直到找到一個空位,或者沒找到然後索引回到了衝突發生的位置,這時會進行擴容然後再重新執行上述插入流程。
查詢也是一樣的,首先通過hash函數計算得到元素應該在的位置,然後從這個位置開始一個個比較key是否相等,遇到被刪除的元素就跳過,遇到空的slot就停止搜尋,這表示元素不在這個雜湊表中。
可以看到大多數操作都需要從某個位置開始一個個向後比較,這就是它得名線性探測的原因。
這種方法實現的hash表可以是一個陣列,它的結構大致如下:

淡藍色的仍然是沒有元素的空位。值得注意的是虛線標記的被刪除元素。
元素是不能直接刪除後把slot設定為空的,那樣會破壞查詢的流程,例如上面圖裡如果把K2刪瞭然後slot設定成空,那你就永遠找不到K3了。所以需要把slot設定成「已刪除」。
插入的時候可以複用「已刪除」的slot,但需要先檢查key是否存在,否則還是上面那個例子,刪除K2後我們想插入一個K3,實際上K3已經存在,但因為他本身應該在的slot空了出來,如果不提前檢查的話插入操作就會把新的K3存進錯誤的位置,此時一張雜湊表裡會有兩個K3,資料混亂了。這裡得批評下github上某本很受歡迎的演演算法書,它在給出的insert範例裡沒考慮這種問題,這導致了它給出的程式碼在一些情況下會導致錯誤的結果。
這裡只是簡單複習,更詳細的程式碼實現可以看這篇。
時間複雜度上和連結串列法差不多,我們來看看優缺點:
優點:
- 對快取友好,現在可以用陣列或者vector之類的可以在記憶體裡緊密排列的結構實現雜湊表
- slot的利用率高,因為元素是存在slot裡的,不過這也不全是好事,後面細說
- 相對來說更節約記憶體,當然是和最原始的連結串列法實現相比,和用大連結串列串聯過的比優勢不是很明顯,原因在缺點裡細說
缺點:
- 實現複雜,一個slot得分有元素、空、元素被刪除三種狀態
- hash衝突是連鎖式的,一處衝突可能會連續影響多處,最終導致插入同樣的資料,它擴容的次數會比連結串列法更多,最終可能會用掉更多的記憶體
- 因為衝突會造成後續插入和刪除的連鎖反應,所以查詢過程退化到
O(n)的概率更大,而且沒法像連結串列法那樣把有大量衝突的地方轉換成搜尋樹之類的結構 - 沒有指標穩定性,這倒也不是太大的缺點,只有c++標準強制要求標準庫的hashmap要有指標穩定性
因為刪除元素麻煩,加上衝突會有連鎖影響,所以很多庫實現的hashtable都是用的連結串列法。不過即使有這麼多缺點,光快取友好和記憶體利用率高在現代計算機上就是非常大的效能優勢了,所以像golang和python都會使用線性探測法的近似變種來實現雜湊表。
SwissTable簡介
我們複習了兩種常見的雜湊表實現,它們要麼浪費記憶體且對快取不友好;要麼發生衝突後會更容易導致查詢、插入、刪除操作效能下降。這還是在有「完美雜湊函數」的情況下,如果你用了個不那麼好的雜湊函數,那會導致key衝突的概率大大上升,效能問題會更加明顯,最壞的情況下效能甚至會不如在陣列裡進行線性搜尋。
自然而然地,業界開始尋找一種既對快取友好又不會讓查詢效能退化的太厲害的雜湊表演演算法。大多數人的研究方向是開發更好的雜湊函數,在讓雜湊函數不斷接近「完美雜湊函數」的品質的同時用各種手段優化計算效能;另外一些人在改進雜湊表本身的結構力求在快取友好、效能和記憶體用量上找到平衡。swisstable就屬於後者。
swisstable的時間複雜度和線性探測法的差不多,空間複雜度介於連結串列法和線性探測之間。
swisstable的核心思想是hashtable的大部分操作都是圍繞雜湊函數計算得到的結果和slot的狀態(是否能存資料是否有目標資料在slot裡)進行的,而要知道這些資訊不需要整個slot的資料,因此把這些操作需要的資訊提取出來作為元資訊進行操作,記憶體效率和CPU效率都可以優於直接操作存放完整資料的slot。
swisstable的實現有很多,我們主要基於將這個資料結構推廣壯大的abseil庫的實現進行簡要的介紹,有關這個實現,cppcon中的演講比我更詳細,可以去看看,文末會給出連結。不過我講的可能和這兩個演講的內容有些出入,比較又過了好幾年,程式碼庫總是要隨著時代變化而發展的。
SwissTable的結構
別看這名字都把hash改沒了,實際上swisstable依然是hashtable,而且使用改進的線性探測法來解決hash衝突。
所以大家應該能想象到,swisstable的底層應該也是個類似陣列的結構。有了這樣大致的模糊印象就可以了,現在我們可以來看看swisstable的結構了:

圖裡東西挺多,但基本都有詳細的註釋,對於一些比較重要的東西我會稍微再重複講解一遍。
首先是雜湊函數計算的結構,在swisstable裡會被分成兩部分:57bits長度的為H1,用於確定元素存在哪個slot裡,slot的索引和control bytes的是對應的;剩下的7bits叫做H2,被用作是當前key的雜湊特徵值,用於後面的查詢和過濾。
接著是swisstable的主體結構,實際上就是一塊連續的記憶體,但除了slot外還在頭部帶有描述每個slot狀態的控制資訊,以及為了記憶體對齊而放進去的填充資料。
swisstable比傳統雜湊表更快的祕訣就在於這些被叫做「control bytes」的slot控制資訊裡,即前面說的「元資訊」。
控制資訊主要是下面這幾種:
- slot是否為空
- slot裡的元素是否已經被刪除
- slot裡存的鍵值對的key的雜湊特徵(H2)
對於空、刪除和邊界這幾種特殊狀態,對應的值都是特意設定的,目的是為了在SIMD指令操作時獲得最高的效能,如果你想自己實現swisstable,注意這些狀態值需要和圖裡給的一樣(或者你也可以找到在X86和ARM以外的平臺上的最佳值並使用它們)。
查詢、插入、刪除都是基於這些control bytes的,它們非常小,可以儘量多的被放入CPU的快取記憶體,同時又包含了足夠的資訊以滿足雜湊表的增刪改查。而slot就只用來存資料,control bytes和slot一一對應,控制資訊在control bytes裡的索引就是對應的資料在slot裡的索引。
另外還可以看到圖裡還有一個group的結構,這個結構沒有實體存在(雖然在abseil的實現裡有對應的類存在),它由連續的N個控制資訊組成,swisstable的線性探測是以group為基礎單位的,一次探測一個group,沒有找到目標就會移動到下一個group繼續查詢。現在看不懂也沒關係,下節會簡要說明查詢的演演算法。
到目前為止我們瞭解了swisstable的結構,至於它為什麼這麼快,有一個比較次要的原因我們已經知道了:所有的操作基本都在control bytes上進行,一個控制資訊只有8bit,而且控制資訊們緊密排列在連續的記憶體裡對快取更友好,所以雜湊表操作時的快取命中率會更高,客觀上會提高一點效能。但這不是swisstable最精明的地方,我們接著看看查詢一個元素的過程。
在進入下一節之前我還有另外一個重要的說明需要做:對於control bytes以及對它的操作,我會用前後左右這種方位詞,但實際上操作control bytes時要考慮的不是方位而是記憶體的高低位以及位元組序,後者會影響到索引的計算方式,為了方便敘述我故意省略了這些細節而使用「前後左右」,我的圖也是按照從左到右從前往後的順序繪製的,如果要考慮這些圖會畫的比較複雜,演演算法的描述也將變得繁瑣,因此請原諒我偷一個小小的懶。
SwissTable的查詢
提高CPU快取命中率可以極大提升效能,但不會達到很多效能測試裡展示的那種雲泥之別。所以swisstable的快主要體現在別的地方——更巧妙的查詢演演算法。
上一節我們已經提到了group,swisstable會根據H1的值來確定group的起始位置,然後按照一個個group去做「線性探測」。
假設我們有一個key叫Key1,它已經存在了swisstable裡,這時候swisstable裡的區域性資料是下面那樣的:
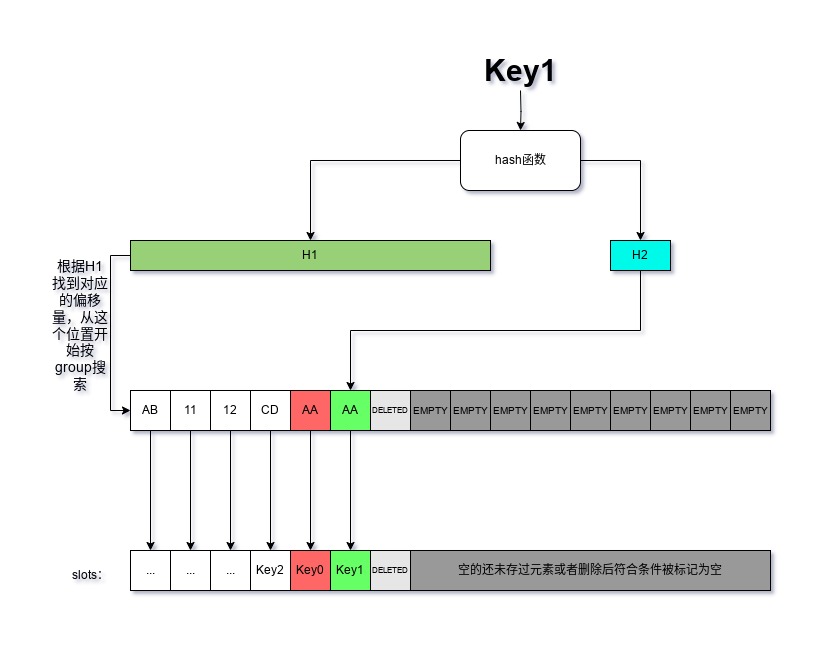
我們要找的資料正好在這個group裡,但還有另一個key的雜湊特徵和我們要找的目標衝突了。按照正常的線性探測法的流程,我們應該根據這個group裡的控制資訊的索引,找到對應的slot,然後把裡面的key拿出來一一做相等比較,直到找到我們要的目標,在這裡我們需要相等比較六次。
這樣也太小看人類的智慧了,下面才是真正的比較過程,也是swisstable的精華:

事實上swisstable會先一次比較一整個group裡的雜湊特徵資訊,先把特徵值不相等的元素全部排除,特徵值不相等那說明key肯定不會相等。
這樣一次檢查了16個值,在這個例子裡我們過濾出了兩個需要檢查的索引值,相等比較的次數一次減少了三分之二。上面這樣的比較藉助現代CPU的SIMD功能,只需要三到四條指令即可完成。
將雜湊特徵比較結果轉換成uint32的整數也是很巧妙的一步。不轉化的話我們仍然需要遍歷去尋找有效的資料的索引,然而轉換成數位之後我們只需要去計算這個數位的二進位制資料裡有多少個尾隨的0即可,這在大部分平臺上都只需要一條指令就能完成;想要查詢下一個有效的所以,只需要一個小小的位運算技巧就可以把上次找到的為1的位轉換成0,然後再次計算尾隨0的數量即可。整體會比遍歷快很多倍。
如果當前的group裡沒找到,那麼就會移動到下一個group,重複上面的步驟,直到找到資料或者遇到了control bytes的結束標誌。
這個例子裡我們在第一個group裡就找到了,而且運氣很好只需要一次相等比較(這裡計算尾隨0的話會導致從後往前檢查詢到的索引,我們要找的Key1正巧在最後面),而普通的線性探測需要相等比較6次。
這就是swisstable擁有驚人效能的主要原因:它儘量避免線性探測法導致的大量等值比較和連結串列法會帶來的快取命中率低下,以及在單位時間內它能同時過濾N個(通常為16,因為16x8=128,是大多數平臺上SIMD指令專用的向量暫存器的大小)元素,且可以用位運算代替對資料的遍歷。這會為雜湊表的吞吐量帶來質的飛躍。
SwissTable的插入、更新和刪除
因為swisstable本質是使用了改進了的線性探測法,因此一些線上性探測法中遇到的問題在這裡也跑不掉。所以插入、更新和刪除都得基於上一節介紹的查詢。
所以對於插入和更新,演演算法的大致步驟是這樣的:
- 利用查詢的過程嘗試找到目標key,如果存在那就直接進行更新
- 不存在的時候會選擇合適的有空位的group,當前group沒有位置的時候就會順延到下一個group,這步和線性探測一樣
- 然後選擇有空位的group裡最左側的一個空位(控制資訊顯示為刪除或者空的slot),寫入控制資訊,然後把key和value插入對應的slot(這裡的左側只是個形象的說法,實際上根據實現的不同略有出入,但group是一次比較一整組的,所以相對順序通常沒有那麼重要)
- 如果沒找到合適的空位,先嚐試把標記為delete的slot按演演算法將符合條件的標記為空,依然沒有合適的空位則會嘗試擴容,然後再插入
查詢是否有合適的空位和將標記為刪除的slot更新為empty這兩個操作都是藉助SIMD指令和位運算批次完成的。
刪除的操作需要考慮一些邊界條件,併為減少記憶體使用量做了一些優化:
- 根據給的key找到對應的control byte和slot
- 將slot裡存的資料釋放掉,slot本身保留
- 將control byte從雜湊特徵值改成表示資料被刪除的標記值
- 這步是優化,會判斷control byte前後的資料,符合條件的情況下可以不標記為被刪除,直接標記為empty。
當然了,設定control byte的值用的是位運算,而檢查是否符合直接標記為空的操作也藉助了SIMD。
從這三個操作來看,SwissTable快的原因還在於:所有可以利用SIMD進行批次操作的地方都進行了對應的優化。
所以SwissTable為什麼這麼快?
看完SwissTable的實現,我覺得可以總結為下面幾點:
- 對hashtable的操作從slot轉移到了control bytes上,控制資訊更小更容易被填入CPU的快取記憶體,因此比直接在slot上操作更快,即使需要多付出一次從control bytes得到索引後再去參照slot的代價
- 記錄雜湊特徵值,減少了無意義的key等值比較,這是線性探測法效能下降的主要元凶
- 對slot的查詢和操作是通過control bytes批次進行的,單位時間內吞吐量有顯著提升
- 標誌位的值和整個資料結構的記憶體佈局都為SIMD進行了優化,可以充分發揮效能優勢
- 對slot也有優化,比如對太大的資料會壓縮儲存以提高快取命中率,不過這只是錦上添花
還有一些abseil特有的優化,比如根據table的大小選擇更合適的擴容策略來平衡效能和記憶體效率。這些不是swisstable演演算法的一部分,就不列進去了。
在解決了空間區域性性問題的基礎上,swisstable還利用了現代CPU的特性批次操作元素,所以效能會有飛躍般的提升。
如果CPU沒有對應的SIMD指令怎麼辦
swisstable需要的主要是sse2的指令,這些指令最早在2000年由Intel釋出,目前X86平臺上常見的處理器都支援,20年前釋出的處理器還在執行的已經非常稀有了。
在ARM平臺上比較特殊,雖然有NEON這樣的SIMD指令集存在,但缺少一部分SSE2的功能,雖然可以靠位運算修補,但整體要比X86上多花幾條指令。以及NEON的普及程度較SSE2稍差,新的晶片上應該都支援,但稍微老一些的裝置和部分嵌入式裝置/單板計算機就夠嗆了。
最麻煩的是一些不支援演演算法要求的SIMD指令的平臺。當然也不是沒辦法,實際上swisstable演演算法中描述的批次操作可以靠位運算實現,其中查詢的操作還可以一次批次處理8條資料。但吞吐量直接腰斬,一次查詢需要的指令數也大幅超過了能使用SIMD的平臺,粗略看了下至少得多用三倍的指令,這會帶來一些效能衰退。
不過快取友好和批次操作帶來的好處還是可以體驗到一部分的,所以即使CPU不支援需要的SIMD指令,你依舊能從swisstable中獲益。
SwissTable還有什麼需要注意的地方
對於使用者來說只有一個需要注意的地方:如果你要自定義key的雜湊函數,一定得提供一個質量最上乘的。因為現在雜湊函數計算出來的值除了要讓資料儘量均勻分佈之外,還得儘量保證每一個bit的概率均等性,也就是儘量接近前面說的「完美雜湊函數」,否則雜湊特徵值會出現很多重複值,這樣即使有再多的批次操作,還是會被大量等值比較拖慢速度。不過這也有上限,最低也差不多在1/128,因為我們就用了七位雜湊值。如果我們用了個質量堪憂的雜湊函數,這個重複率就可能變成1/20,SIMD帶來的效能優勢可能就蕩然無存了。
對於想實現swisstable的人來說,注意點會稍微多一些。
第一點是注意記憶體對齊,SSE2要求操作的記憶體地址是對齊過的,如果不是它會自己轉換,這個轉換非常耗時。所以abseil的實現上不僅分配的時候處理對齊,還用填充資料保證了這一點。
第二點的slot的個數,選擇了不合適的slot數量會導致H1定位衝突的增加,因此像abseil選擇了2**N-1作為slot的數量,擴容也是按照N∈{1, 2, 3, 4, ...}這樣的方式擴容的。
第三點,用作存放控制資訊的資料型別大小最好是8bit,多了浪費少了不能充分表示資訊並加大了衝突概率,而且這8bit必須是全部可以使用的;如果用的是c/c++,那麼char不能用,因為char是否帶符號是平臺和編譯器定義的,沒有可移植性,不用unsigned char是因為標準只規定了它的最小大小,沒規定上限,所以不如intN_t這樣的型別來的保險。可以學abseil用int8_t。
總結
整篇文章其實還忽略了一個影響hashtable演演算法效能的點:雜湊函數的演演算法。因為我們開篇就假設了我們有「完美雜湊函數」,所以沒有對這點進行過多討論。現實是雜湊函數的效能也很重要,但討論怎麼優化它的效能超出了本文的討論範圍。比較常見的優化方向其實和swisstable在實現查詢時用的辦法差不多:依賴SIMD增加資料吞吐量或者利用硬體指令(AES、SHA系列)來加速計算。詳細的就不做展開了。
如果要說swisstable有什麼缺點,那應該只有高度依賴雜湊函數的品質這一點了,依賴SIMD其實不是什麼大問題,現代CPU都支援,新興的平臺比如RISC-V和LoongArch都有活躍的社群和維護者,隨著時間推進提供對等的支援不是太遠的事,但雜湊函數的品質是很難控制的,何況雜湊函數可以使用一些使用者自己實現的。使用者想避免這類問題,最好的辦法就是用現成的被證明品質良好的雜湊演演算法,比如murmur3或者用庫裡提供的,而不是自己去寫。
swisstable正在逐漸被業界接納,例如rust就已經把它內建進標準庫了;golang最後是否會接受swisstable還是未知數,不過swisstable本身最早就是谷歌設計和實現的,帶來的提升也是實打實的,我想官方最終接納的可能性還是比較大的。
參考資料
首次提出swisstable的cppcon演講:https://www.youtube.com/watch?v=ncHmEUmJZf4
兩年後針對swisstable演演算法的一些改進:https://www.youtube.com/watch?v=JZE3_0qvrMg
swisstable用到的位運算可以參考這篇,原理上基本一樣:https://methane.hatenablog.jp/entry/2022/02/22/Swisstable_Hash_に使われているビット演算の魔術
前面提到的即使沒有SIMD也可以同時處理8個控制資訊,使用的位運算參考這篇:http://graphics.stanford.edu/~seander/bithacks.html