【調變解調】PM 調相

說明

學習數位訊號處理演演算法時整理的學習筆記。同系列文章目錄可見《DSP 學習之路》目錄，程式碼已上傳到 Github - ModulationAndDemodulation。本篇介紹 PM 調相訊號的調變與解調，內附全套 MATLAB 程式碼。

1. PM 調變演演算法

1.1 PM 訊號描述

用調變訊號去控制載波的瞬時相位，使其按照調變訊號的規律變化，當調變訊號是模擬訊號時，這個過程就被稱為調相（PM）。在 FM 調頻與 PM 調相的過程中，載波的幅度都保持恆定不變，而頻率和相位的變化都表現為載波瞬時相位的變化，故把調頻和調相統稱為角度調變，與幅度調變技術相比，角度調變最突出的優勢是其較高的抗噪聲效能，然而獲得這種優勢的代價是角度調變佔用比幅度調變訊號更寬的頻寬。PM 訊號的時域表示式為：

\[s_{PM}(t)=Acos{\left[\omega_ct+{K_p}m(t)\right]} \tag{1} \]

式中：\(A\) 為載波恆定振幅，\(K_p\) 為調相靈敏度（單位 \(rad/V\)），\(m(t)\) 是調變訊號（攜帶要發出去的資訊），\(cos{\omega_ct}\) 是載波，\(\omega_c\) 是載波角頻率，與載波頻率 \(f_c\) 之間的關係為 \(\omega_c=2{\pi}f_c\)。由式 \((1)\) 可得 PM 訊號相對於載波相位 \({\omega}_ct\) 的瞬時相位偏移為：

\[\varphi(t)={K_p}m(t) \tag{2} \]

由 \((1)\) 式可知 PM 訊號相對於載波相位 \({\omega}_ct\) 的瞬時相位偏移隨 \(m(t)\) 呈線性變化，比例係數為 \(K_p\)。PM 訊號與 FM 訊號有很多相同之處，如果預先不知道調變訊號 \(m(t)\) 的具體形式，則無法判斷已調訊號是 PM 訊號還是 FM 訊號。PM 訊號的調相指數（調變指數）\(\beta\) 被定義為最大的相位偏移：

\[\beta={K_p}{\lvert}{m(t)}{\rvert}_{max} \tag{3} \]

若 \(m(t)\) 為單一頻率的正弦波（即 \(m(t)={A_m}cos({2{\pi}{f_m}t})\)），則調變指數的表示式如下。

\[{\beta}={K_p}{\lvert}{m(t)}{\rvert}_{max}={K_p}{A_m} \tag{4} \]

1.2 PM 訊號調變範例

與 FM 訊號一樣，PM 訊號的調變方法也可分為 3 種，一種是直接調相法，一種是間接調相法，第三種是正交調變法。

（1）直接調相法

直接調相法是用調變訊號 \(m(t)\) 直接改變諧振迴路的引數，使載波訊號通過諧振迴路時產生相移而形成調相波，最常用的直接調相電路是變容二極體調相器。

（2）間接調相法

間接調相電路比直接調相電路複雜，由於頻率與相位之間存在微分與積分的關係，所以 FM 與 PM 之間是可以相互轉換的。先對調變訊號進行微分，然後對微分結果進行調頻，就得到了調相訊號，這種方式叫間接調相。先對調變訊號進行積分，然後對積分結果進行調相，就得到了調頻訊號，這種方式叫間接調頻。

（3）正交調變法

將 \((1)\) 式進行三角展開，可以得到：

\[\begin{aligned} s_{PM}(t)&=Acos{\left[\omega_ct+{K_p}m(t)\right]}\\[1em] &=Acos{(\omega_ct)}cos{\left[{K_p}m(t)\right]}-Asin{(\omega_ct)}sin{\left[{K_p}m(t)\right]}\\[1em] \end{aligned} \tag{5} \]

正交調變流程如下，其中第 2 步也可以先將 \(I(t)\) 和 \(Q(t)\) 組成一個覆信號 \(Z(t)=I(t)+iQ(t)\)，然後乘以覆載波 \(exp(i\omega_ct)\)，最後取實部，即 \(s_{PM}(t)=Real\left[Z(t)exp(i\omega_ct)\right]\)，兩種方法是等價的。：

對調變訊號 \(m(t)\) 分別取餘弦和正弦，得到 \(I\) 路資料 \(I(t)=cos{\left[{K_p}m(t)\right]}\) 與 \(Q\) 路資料 \(Q(t)=sin{\left[{K_p}m(t)\right]}\)。
分別乘以載波 \(Acos(\omega_ct)\) 與 \(-Asin(\omega_ct)\) 後相加，得到 PM 訊號 \(s_{PM}(t)=I(t)Acos(\omega_ct)-Q(t)Asin(\omega_ct)\)。

調變訊號 \(m(t)\) 可以是確知訊號，也可以是隨機訊號。當 \(m(t)\) 是確知訊號時，不妨假設 \(m(t)\) 的時域表示式如下：

\[m(t) = sin(2{\pi}{f_m}t)+cos({\pi}{f_m}t) \tag{6} \]

各調變引數取值：\(A=1\)，\(f_m=2500Hz\)，\({\beta}=4\)，\(f_c=20000Hz\)。訊號取樣率 \(f_s=8{f_c}\)，模擬總時長為 \(2s\)。PM 調變效果如下圖所示（為了美觀，時域只顯示前 500 個點），調變訊號 \(m(t)\) 雙邊幅度譜有四根離散譜線（\({\pm}2500Hz\)、\({\pm}1250Hz\)），載波 \(c(t)\) 的雙邊幅度譜有兩根離散譜線（\({\pm}20000Hz\)），程式碼詳見附錄 main_modPM_example.m 與 mod_pm.m，設定 beta = 4 即可。

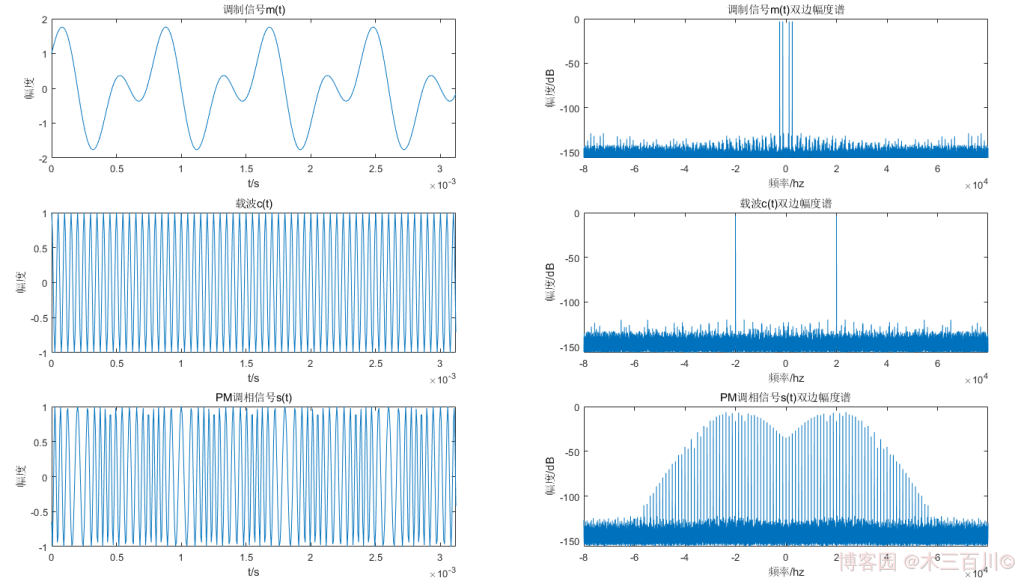
2. PM 解調演演算法

解調是調變的逆過程，其作用是從接收的已調訊號中恢復原基頻訊號（即調變訊號）。PM 解調時，可以先使用 FM 解調器，然後對解調結果進行積分。另一種思路是直接提取 PM 訊號的相位資訊，有希爾伯特變換法以及數位正交解調法。下面分別用幾種不同方法對 1.2 節中確知訊號的 PM 調變結果進行解調。

2.1 FM 解調積分法

FM 訊號的解調詳見本人同系列部落格【調變解調】FM 調頻，內有 FM 解調器相關程式碼。這種方法的流程如下：

第一步：進行 FM 解調。
第二步：對 FM 解調結果進行積分。
第三步：去除直流分量（減去自身均值）。

對 1.2 節中的 PM 訊號，設定訊雜比 \(SNR=50dB\)，解調效果如下，解調後幅度放大係數 \(k=\overline{{\lvert}m(t){\rvert}}/\overline{{\lvert}\hat{m}(t){\rvert}}\approx70439.28\)，使用這個係數放大解調訊號幅值，然後計算誤差，有：\(\sqrt{\sum{{\lvert}m(t_i)-k\hat{m}(t_i){\rvert}^2}}/\sqrt{\sum{{\lvert}m(t_i){\rvert}^2}}\approx0.0388\)。

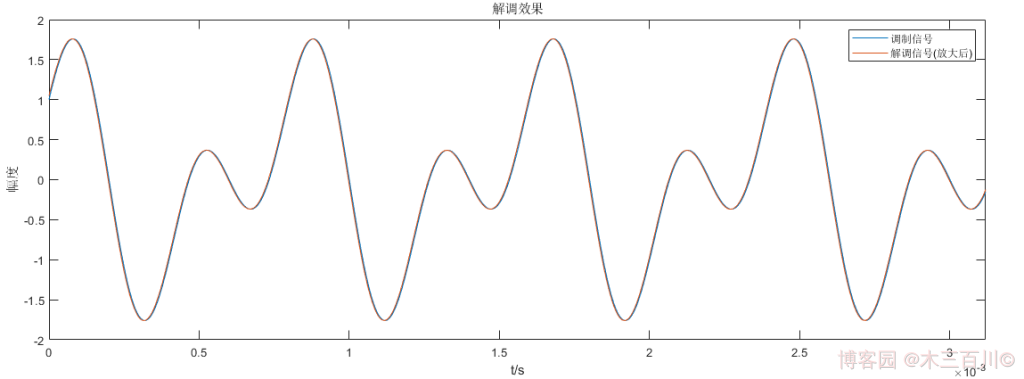
程式碼詳見 demod_pm_method1.m 和 main_demodPM_example1.m，調頻解調器的程式碼詳見本人同系列部落格【調變解調】FM 調頻。

2.2 希爾伯特求瞬時相位法

可以通過希爾伯特變換的方法求得 PM 訊號的瞬時相位，然後減去由載波導致的線性分量 \({\omega_ct}\)，獲得非線性瞬時相位，也就是相對於載波相位 \({\omega}_ct\) 的瞬時相位偏移。這種方法的流程如下：

第一步：計算 \(s(t)\) 的希爾伯特變換，得到一個覆信號（實部為 \(s(t)\)，虛部為其希爾伯特變換結果），對所得覆信號求相位角並去卷疊，得到 PM 訊號的瞬時相位 \({\phi}(t)\)。
第二步：減去由載波導致的線性分量 \(\omega_ct\) 以及載波初相 \(\varphi_0\)，得到解調結果 \(m_o(t)={\phi}(t)-\omega_ct-\varphi_0\)。

對 1.2 節中的 PM 訊號，設定訊雜比 \(SNR=50dB\)，解調效果如下，解調後幅度放大係數 \(k=\overline{{\lvert}m(t){\rvert}}/\overline{{\lvert}\hat{m}(t){\rvert}}\approx0.44\)，使用這個係數放大解調訊號幅值，然後計算誤差，有：\(\sqrt{\sum{{\lvert}m(t_i)-k\hat{m}(t_i){\rvert}^2}}/\sqrt{\sum{{\lvert}m(t_i){\rvert}^2}}\approx0.0010\)。

程式碼詳見 demod_pm_method2.m 和 main_demodPM_example2.m。

2.3 數位正交解調

數位正交解調屬於相干解調的一種，但這種方法具有較強的抗載頻失配能力，不要求相干載波嚴格的同相。PM 數位正交解調一般有以下四個步驟：

第一步：乘以正交相干載波得到 \({s_I}(t)\) 與 \({s_Q}(t)\)，即 \({s_I}(t)=s(t)cos({\omega_ct}+{\phi_0})\)，\({s_Q}(t)=-s(t)sin({\omega_ct}+{\phi_0})\)。
第二步：低通濾波器濾除 \({s_I}(t)\) 與 \({s_Q}(t)\) 中的高頻分量。
第三步：通過反正切函數計算相位，得到解調結果 \(m_o(t)=atan\left[\frac{s_Q(t)}{s_I(t)}\right]=km(t)+\Delta\phi\)。
第四步：去除直流分量（減去自身均值）。

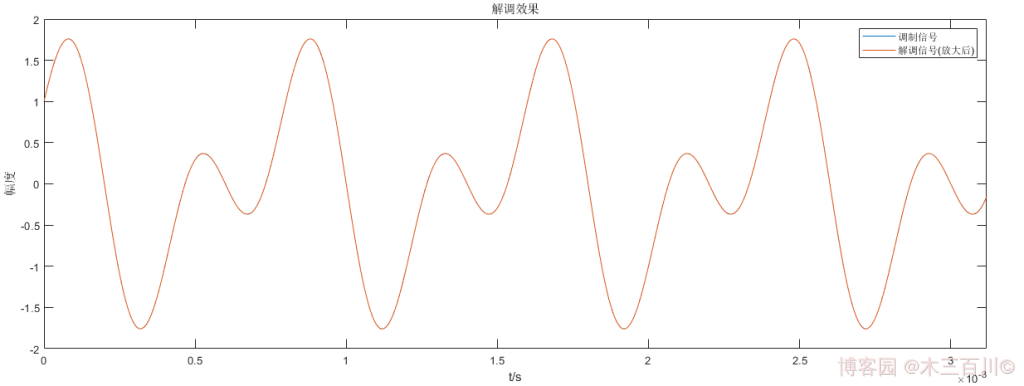
程式碼詳見 demod_pm_method3.m 和 main_demodPM_example3.m。更改相干載波的初始相位為 \({\phi_0}=\pi/4,\pi/2\) 後，解調效果依然很好；但更改相干載波的中心頻率為 \(0.8f_c,1.2f_c\) 後，解調效果變得很差，說明這種方法具有較好的抗載頻相位失配能力。

3. PM 模擬（MATLAB Communications Toolbox）

MATLAB 的 Communications Toolbox 中提供了 PM 調變函數 pmmod，高斯白噪聲函數 awgn，以及 PM 解調函數 pmdemod，可以很方便地完成 PM 訊號模擬。使用這三個函數實現上面 1.2 節中確知訊號 \(m(t)\) 的 PM 調變解調（將調相指數 \(\beta\) 改為 \(1\)），調變後加噪聲的效果如下：

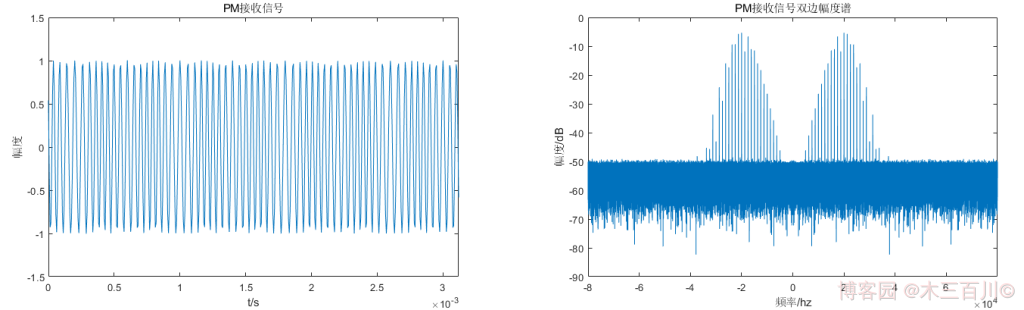
解調效果如下：

解調訊號與調變訊號波形基本重回，計算誤差，有：\(\sqrt{\sum{{\lvert}m(t_i)-\hat{m}(t_i){\rvert}^2}}/\sqrt{\sum{{\lvert}m(t_i){\rvert}^2}}\approx0.0022\)。程式碼詳見附錄 main_CommPM_example.m。

參考資料

[1] 樓才義,徐建良,楊小牛.軟體無線電原理與應用[M].電子工業出版社,2014.

[2] 樊昌信,曹麗娜.通訊原理.第7版[M].國防工業出版社,2012.

[3] 劉學勇.詳解MATLAB/Simulink通訊系統建模與模擬[M].電子工業出版社,2011.

[4] 王麗娜,王兵.衛星通訊系統.第2版[M].國防工業出版社,2014.

附錄程式碼

附.1 檔案 mod_pm.m

function [ sig_pm ] = mod_pm(fc, beta, fs, mt, t, A)
% MOD_PM        PM 調相
% 輸入引數：
%       fc      載波中心頻率
%       beta    調頻指數/調變指數
%       fs      訊號取樣率
%       mt      調變訊號
%       t       取樣時間
%       A       載波恆定振幅
% 輸出引數：
%       sig_pm  調相(PM)實訊號
% @author 木三百川

% 計算調相靈敏度
Kp = beta/max(abs(mt));

% 生成訊號
ct = A*cos(2*pi*fc*t);           % 載波 
sig_pm = A*cos(2*pi*fc*t+Kp*mt); % PM調相訊號

% 繪圖
nfft = length(sig_pm);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm));
subplot(3,2,1);
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('調變訊號m(t)');
subplot(3,2,2);
plot(freq, 10*log10(fftshift(abs(fft(mt,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('調變訊號m(t)雙邊幅度譜');

subplot(3,2,3);
plot(t(1:plot_length), ct(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('載波c(t)');
subplot(3,2,4);
plot(freq, 10*log10(fftshift(abs(fft(ct,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('載波c(t)雙邊幅度譜');

subplot(3,2,5);
plot(t(1:plot_length), sig_pm(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM調相訊號s(t)');
subplot(3,2,6);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('PM調相訊號s(t)雙邊幅度譜');

end

附.2 檔案 main_modPM_example.m

clc;
clear;
close all;
% PM 調變模擬(調變訊號為確知訊號)
% @author 木三百川

% 調變引數
A = 1;                  % 載波恆定振幅
fm = 2500;              % 調變訊號引數
beta = 4;               % 調相指數/調變指數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 取樣率
total_time = 2;         % 模擬時長，單位：秒

% 取樣時間
t = 0:1/fs:total_time-1/fs;

% 調變訊號為確知訊號
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% PM 調變
[ sig_pm ] = mod_pm(fc, beta, fs, mt, t, A);

附.3 檔案 lpf_filter.m

function sig_lpf = lpf_filter(sig_data, cutfre)
% LPF_FILTER    自定義理想低通濾波器
% 輸入引數：
%       sig_data        待濾波資料
%       cutfre          截止頻率，範圍 (0,1)
% 輸出引數：
%       sig_lpf         低通濾波結果
% @author 木三百川

nfft = length(sig_data);
lidx = round(nfft/2-cutfre*nfft/2);
ridx = nfft - lidx;
sig_fft_lpf = fftshift(fft(sig_data));
sig_fft_lpf([1:lidx,ridx:nfft]) = 0;
sig_lpf = real(ifft(fftshift(sig_fft_lpf)));

end

附.4 檔案 demod_pm_method1.m

function [ sig_pm_demod ] = demod_pm_method1(sig_pm_receive, fc, fs, t, phi0)
% DEMOD_PM_METHOD1        PM 解調(FM 解調積分法)
% 輸入引數：
%       sig_pm_receive      PM 接收訊號，行向量
%       fc                  載波中心頻率
%       fs                  訊號取樣率
%       t                   取樣時間
%       phi0                相干載波初始相位
% 輸出引數：
%       sig_pm_demod        解調結果，與 sig_pm_receive 等長
% @author 木三百川

% 第一步：進行 FM 解調
[ sig_pm_demod ] = demod_fm_method4(sig_pm_receive, fc, fs, t, phi0);

% 第二步：對 FM 解調結果進行積分
sig_pm_demod = cumtrapz(t, sig_pm_demod);

% 第三步：去直流
sig_pm_demod = sig_pm_demod - mean(sig_pm_demod);

end

附.5 檔案 main_demodPM_example1.m

clc;
clear;
close all;
% PM 解調模擬(調變訊號為確知訊號，FM 解調積分法)
% @author 木三百川

% 調變引數
A = 1;                  % 載波恆定振幅
fm = 2500;              % 調變訊號引數
beta = 4;               % 調相指數/調變指數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 取樣率
total_time = 2;         % 模擬時長，單位：秒

% 取樣時間
t = 0:1/fs:total_time-1/fs;

% 調變訊號為確知訊號
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% PM 調變
[ sig_pm_send ] = mod_pm(fc, beta, fs, mt, t, A);

% 加噪聲
snr = 50;               % 訊雜比
sig_pm_receive = awgn(sig_pm_send, snr, 'measured');

% FM 解調積分法
ini_phase = 0;
[ sig_pm_demod ] = demod_pm_method1(sig_pm_receive, fc, fs, t, ini_phase);

% 繪圖
nfft = length(sig_pm_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_pm_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM接收訊號');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('PM接收訊號雙邊幅度譜');

coef = mean(abs(mt))/mean(abs(sig_pm_demod));
fprintf('norm(調變訊號 - %.2f * 解調訊號)/norm(調變訊號) = %.4f.\n', coef, norm(mt-coef*sig_pm_demod)/norm(mt));

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), coef*sig_pm_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解調效果');
legend('調變訊號','解調訊號(放大後)');

附.6 檔案 demod_pm_method2.m

function [ sig_pm_demod ] = demod_pm_method2(sig_pm_receive, fc, fs, t, phi0)
% DEMOD_PM_METHOD2        PM 解調(希爾伯特求瞬時相位法)
% 輸入引數：
%       sig_pm_receive      PM 接收訊號，行向量
%       fc                  載波中心頻率
%       fs                  訊號取樣率
%       t                   取樣時間
%       phi0                相干載波初始相位
% 輸出引數：
%       sig_pm_demod        解調結果，與 sig_pm_receive 等長
% @author 木三百川

% 第一步：使用希爾伯特變換計算瞬時相位
inst_phase = unwrap(angle(hilbert(sig_pm_receive)));

% 第二步：去除載波分量
sig_pm_demod = inst_phase - 2*pi*fc*t - phi0;

end

附.7 檔案 main_demodPM_example2.m

clc;
clear;
close all;
% PM 解調模擬(調變訊號為確知訊號，希爾伯特求瞬時相位法)
% @author 木三百川

% 調變引數
A = 1;                  % 載波恆定振幅
fm = 2500;              % 調變訊號引數
beta = 4;               % 調相指數/調變指數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 取樣率
total_time = 2;         % 模擬時長，單位：秒

% 取樣時間
t = 0:1/fs:total_time-1/fs;

% 調變訊號為確知訊號
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% PM 調變
[ sig_pm_send ] = mod_pm(fc, beta, fs, mt, t, A);

% 加噪聲
snr = 50;               % 訊雜比
sig_pm_receive = awgn(sig_pm_send, snr, 'measured');

% 希爾伯特求瞬時相位法
ini_phase = 0;
[ sig_pm_demod ] = demod_pm_method2(sig_pm_receive, fc, fs, t, ini_phase);

% 繪圖
nfft = length(sig_pm_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_pm_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM接收訊號');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('PM接收訊號雙邊幅度譜');

coef = mean(abs(mt))/mean(abs(sig_pm_demod));
fprintf('norm(調變訊號 - %.2f * 解調訊號)/norm(調變訊號) = %.4f.\n', coef, norm(mt-coef*sig_pm_demod)/norm(mt));

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), coef*sig_pm_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解調效果');
legend('調變訊號','解調訊號(放大後)');

附.8 檔案 demod_pm_method3.m

function [ sig_pm_demod ] = demod_pm_method3(sig_pm_receive, fc, fs, t, phi0)
% DEMOD_PM_METHOD4        PM 數位正交解調/相干解調
% 輸入引數：
%       sig_pm_receive      PM 接收訊號，行向量
%       fc                  載波中心頻率
%       fs                  訊號取樣率
%       t                   取樣時間
%       phi0                相干載波初始相位
% 輸出引數：
%       sig_pm_demod        解調結果，與 sig_pm_receive 等長
% @author 木三百川

% 第一步：乘以正交相干載波
sig_pm_i = sig_pm_receive.*cos(2*pi*fc*t+phi0);
sig_pm_q = -sig_pm_receive.*sin(2*pi*fc*t+phi0);

% 第二步：低通濾波
sig_pm_i_lpf = lpf_filter(sig_pm_i, fc/(fs/2));
sig_pm_q_lpf = lpf_filter(sig_pm_q, fc/(fs/2));

% 第三步：計算相位
sig_pm_demod = unwrap(atan2(sig_pm_q_lpf, sig_pm_i_lpf));

% 第四步：去直流
sig_pm_demod = sig_pm_demod - mean(sig_pm_demod);

end

附.9 檔案 main_demodPM_example3.m

clc;
clear;
close all;
% PM 解調模擬(調變訊號為確知訊號，數位正交解調)
% @author 木三百川

% 調變引數
A = 1;                  % 載波恆定振幅
fm = 2500;              % 調變訊號引數
beta = 4;               % 調相指數/調變指數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 取樣率
total_time = 2;         % 模擬時長，單位：秒

% 取樣時間
t = 0:1/fs:total_time-1/fs;

% 調變訊號為確知訊號
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% PM 調變
[ sig_pm_send ] = mod_pm(fc, beta, fs, mt, t, A);

% 加噪聲
snr = 50;               % 訊雜比
sig_pm_receive = awgn(sig_pm_send, snr, 'measured');

% 數位正交解調
ini_phase = 0;
[ sig_pm_demod ] = demod_pm_method3(sig_pm_receive, fc, fs, t, ini_phase);

% 繪圖
nfft = length(sig_pm_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_pm_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM接收訊號');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('PM接收訊號雙邊幅度譜');

coef = mean(abs(mt))/mean(abs(sig_pm_demod));
fprintf('norm(調變訊號 - %.2f * 解調訊號)/norm(調變訊號) = %.4f.\n', coef, norm(mt-coef*sig_pm_demod)/norm(mt));

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), coef*sig_pm_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解調效果');
legend('調變訊號','解調訊號(放大後)');

附.10 檔案 main_CommPM_example.m

clc;
clear;
close all;
% PM 調變解調模擬(使用Communications Toolbox工具箱)
% @author 木三百川

% 調變引數
A = 1;                  % 載波恆定振幅
fm = 2500;              % 調變訊號引數
beta = 1;               % 調相指數/調變指數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 取樣率
total_time = 2;         % 模擬時長，單位：秒

% 取樣時間
t = 0:1/fs:total_time-1/fs;

% 調變訊號為確知訊號
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% FM 調變
ini_phase = 0;
sig_pm_send = A*pmmod(mt,fc,fs,beta,ini_phase);

% 加噪聲
snr = 50;               % 訊雜比
sig_pm_receive = awgn(sig_pm_send, snr, 'measured');

% PM 解調
[ sig_pm_demod ] = pmdemod(sig_pm_receive,fc,fs,beta,ini_phase);

% 繪圖
nfft = length(sig_pm_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_pm_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_pm_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('PM接收訊號');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_pm_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('PM接收訊號雙邊幅度譜');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_pm_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解調效果');
legend('調變訊號','解調訊號');

fprintf('norm(調變訊號 - 解調訊號)/norm(調變訊號) = %.4f.\n', norm(mt-sig_pm_demod)/norm(mt));