並查集和帶權並查集原理
並查集是演演算法競賽中常用的一種資料結構。
它可以高效地處理集合之間的操作與詢問。
其主要功能是查詢兩個元素是否在同一個集合以及將兩個集合合併。
第一部分 並查集的基本操作
演演算法思想
-
我們將所有元素建成很多棵樹(森林),每一棵樹就是一個集合。
-
因為並查集是一個樹結構,那麼每個節點都有一個指標指向父節點。
- 最開始時,每個元素就是一個獨立的集合,每個元素各為一棵樹且自己就是根及自己指向自己。

- 當我們要查詢兩個元素是否在同一個集合時,可以判斷它們是否在同一棵樹上,即只要判斷它們所在樹的根相同與否就可以了。
比如下圖 \(2, 3\) 有相同的根 \(1\),它們便在一個集合,但是 \(2, 9\) 分別擁有根 \(1, 7\),不在同一個集合。
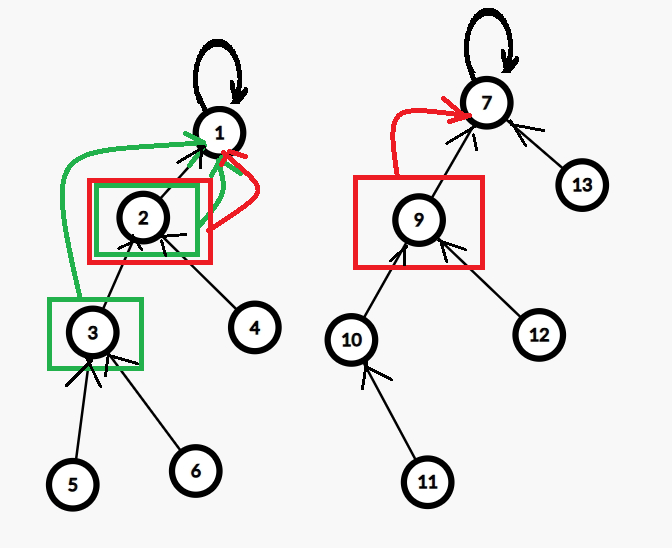
- 當我們要合併兩個集合時,只要兩棵樹合併即可,即只要把兩棵樹的根節點連線起來就可以了。
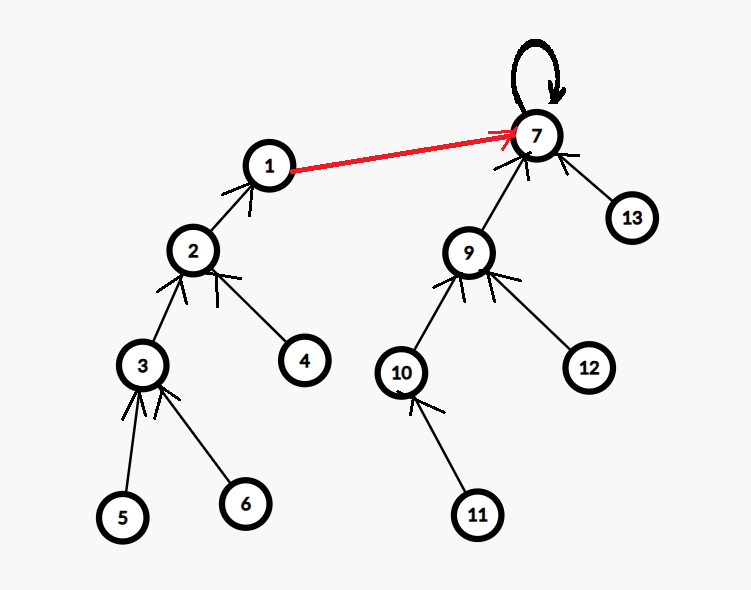
演演算法優化(路徑壓縮)
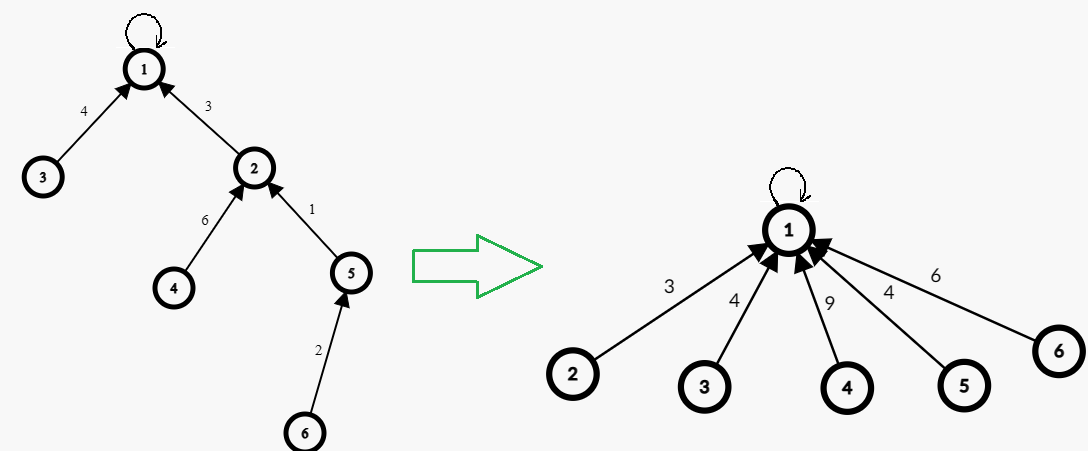
我們發現,如果建出來的樹長這樣:

多次查詢非常費時間,因為每次都可能要從最下面跑到最上面。
因為它們都是一個集合的,不在乎它在集合中的順序或位置,所以我們可以把樹變成這樣:

即每次查詢一個元素在哪一個集合的時候順便把它接在根節點上。
下面我們通過例題講講如何實現該資料結構。
例題
例題1:P3367 【模板】並查集
題目描述

思路
模板題,將上面講述的思路應用到程式碼中即可。
程式碼
#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
int n, m;
int fa[N];
int find(int x) {
if (x == fa[x]) return x;
return fa[x] = find(fa[x]); // 將根節點直接作為 x 點的父親節點
}
void merge(int x, int y) {
int fx = find(x), fy = find(y);
if (fx == fy) return;
fa[fx] = fy; // 將兩個根節點合併
}
void init() {
for (int i = 1; i <= n; i++) fa[i] = i;// 初始化
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
init();
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
if (x == 1) merge(y, z);
else {
if (find(y) == find(z)) cout << "Y\n";
else cout << "N\n";
}
}
return 0;
}
例題2:HDU 1213 How many tables
題目描述

思路
將認識的人合併為一個集合,最後查詢有多少個集合即可。
查詢集合數量有兩種方法:
方法1:等所有操作進行完成以後,我們可以查詢有多少棵樹,也就是查詢有多少個根;
方法2:我們定義 \(cnt\) 初始值為 \(n\),當合並兩個不同的集合時,\(cnt\) 就可以 \(-1\),代表兩個集合合併,集合數量少了一個。
程式碼
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int fa[N];
void init() {
for (int i = 1; i <= n; i++) fa[i] = i;
}
int find(int u) {
if (u == fa[u]) return u;
return fa[u] = find(fa[u]);
}
void merge(int a, int b) {
int fx = find(a), fy = find(b);
if (fx != fy) fa[fx] = fy;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) {
cin >> n >> m;
int cnt = n;
init();
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
if (find(x) != find(y)) cnt--; // 方法2統計結果
merge(x, y);
}
cout << cnt << '\n';
}
return 0;
}
例題3:P3958 [NOIP2017 提高組] 乳酪
題目描述

思路
如果兩個圓的中心相距不超過 \(2R\),\(R\) 為半徑,那麼就將兩個洞合併為一個集合;
如果一個圓的中心與上下表面相距不超過 \(R\),那麼就將洞與上下表面合併;
最後看看上下表面受否在同一個集合,如果在同一個集合,那麼一定可以從下表面走到上表面。
程式碼
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n;
double h, r;
struct pos {
double x, y, z;
} p[N];
int fa[N];
int find(int x) {
if (x == fa[x]) return x;
return fa[x] = find(fa[x]);
}
void merge(int x, int y) {
int fx = find(x), fy = find(y);
if (fx == fy) return;
fa[fx] = fy;
}
double dis(int v1, int v2) {
double x = p[v1].x, y = p[v1].y, z = p[v1].z;
double a = p[v2].x, b = p[v2].y, c = p[v2].z;
return sqrt((x - a) * (x - a) + (y - b) * (y - b) + (z - c) * (z - c));
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) {
cin >> n >> h >> r;
for (int i = 1; i <= n; i++) cin >> p[i].x >> p[i].y >> p[i].z;
for (int i = 0; i <= n + 1; i++) fa[i] = i;
for (int i = 1; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (dis(i, j) <= 2 * r) {
merge(i, j);
}
}
}
for (int i = 1; i <= n; i++) {
if (p[i].z <= r) merge(0, i);
if (p[i].z >= h - r) merge(n + 1, i);
}
if (find(0) == find(n + 1)) cout << "Yes\n";
else cout << "No\n";
}
return 0;
}
例題4:P1111 修復公路
題目描述

思路
我們將所有公路按照修復完成時間從小到大排序,
然後一個一個合併過去,表示公路修好後將兩個村莊可以通車,成為一個集合,
如果什麼時候合併到只有一個集合時,那個時間點就是答案。
程式碼
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
struct road {
int x, y, t;
} r[N];
int n, m;
int fa[N];
int find(int x) {
if (x == fa[x]) return x;
return fa[x] = find(fa[x]);
}
int merge(int x, int y) {
int fx = find(x), fy = find(y);
if (fx == fy) return 0;
fa[fx] = fy;
return 1;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= m; i++) cin >> r[i].x >> r[i].y >> r[i].t;
sort(r + 1, r + m + 1, [](const road a, const road b) { return a.t < b.t; }); // 按照修復完成時間從小到大排序
int cnt = n;
for (int i = 1; i <= m; i++) {
int x = merge(r[i].x, r[i].y);
cnt -= x;
if (cnt == 1) { // 只有一個集合
cout << r[i].t << '\n';
return 0;
}
}
cout << -1 << '\n';
return 0;
}
第二部分 帶權並查集
演演算法思路
即為樹上的每一條邊賦上一個權值,比如邊的長度,維護該節點與父節點的關係。
相應的,當我們進行路徑壓縮的優化時,我們發現所有的節點都接到根上去了,那麼這時每一條邊也自然而然地變成了維護該節點與根節點的關係。
比如權值是是長度時,我們要根據路徑壓縮的結果對路徑權值進行更新:
路徑壓縮時更新權值
還是路徑長度的例子(如上圖),
當我們的父節點 \(f\) 已經被成功合併到根節點時,
我們自然而然地想到如何更新子節點 \(x\) 的距離資訊,
看下面的圖可以幫助理解
有 \(d[x] = d[x_原] + d[f]\),
\(d[x_原]\) 表示 \(x\) 節點與原來的父節點的距離,
\(x\) 現在的的父節點變成了根,所以有:
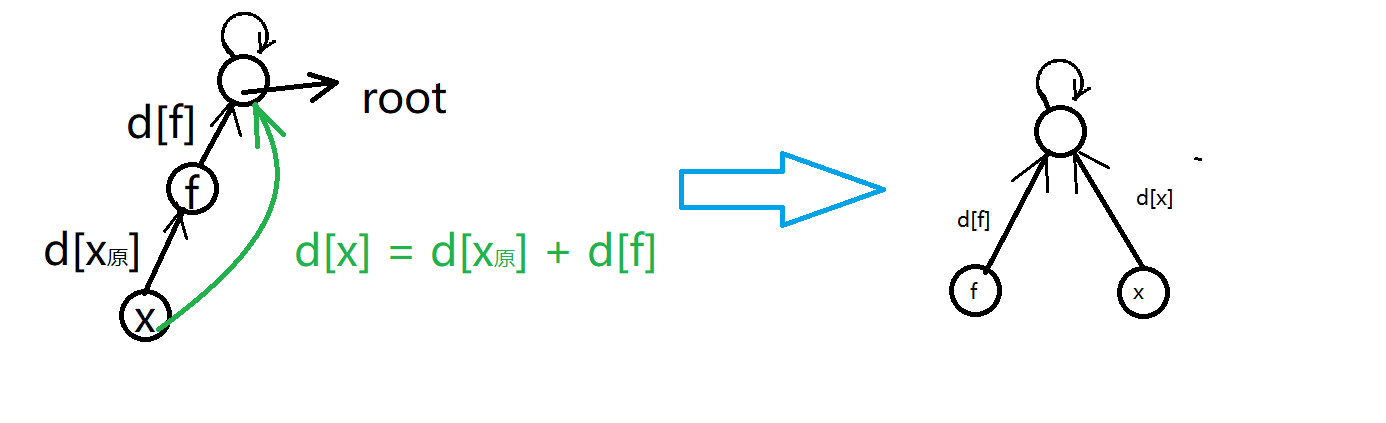
合併時更新權值
合併兩個集合表示兩個集合中的任意兩個點的關係我們都可以知道。
假如給定 \(x\) 點和 \(y\) 點的距離為 \(v\)。
那我們其實已經可以知道 \(x\) 所在子樹和 \(y\) 所在子樹的任意兩個點之間的距離(因為它們都是樹結構)。
然後我們要將 \(x\) 所在集合和 \(y\) 所在集合合併,就可以實現調查任意兩點的關係(距離)
如何處理呢?
我們把 \(x\) 樹接到 \(y\) 上,
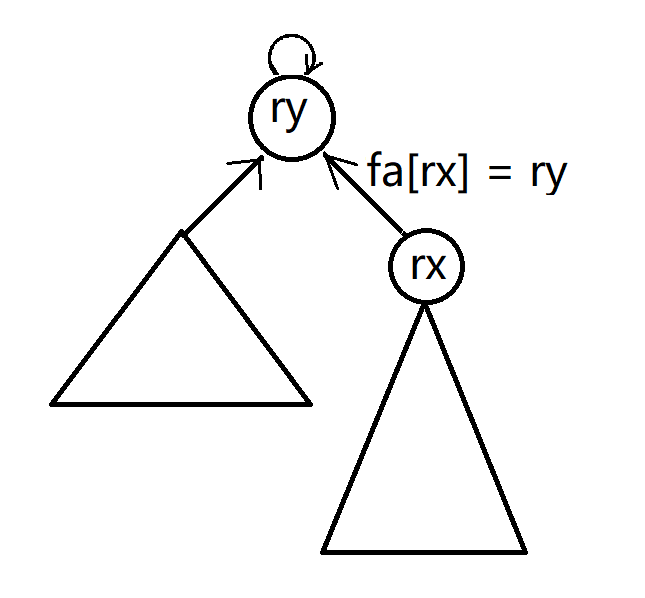
還是直接將 \(x\) 所在子樹的根接到 \(y\) 所在的子樹的根即可。
我們現在開始處理 \(d\) 陣列。
我們發現只要更改一條邊,就是圖中標紅的邊(\(d[rx]\))就夠了:

因為 \(d[rx]\) 被更改了,
其他邊都可以隨著呼叫上面講的 \(find\) 函數進行更新。
怎麼更新 \(d[rx]\) 呢,
我們可以利用高中數學知識(向量)去理解,
容易發現 \(d[rx] = -d[x] + v + d[y]\)。
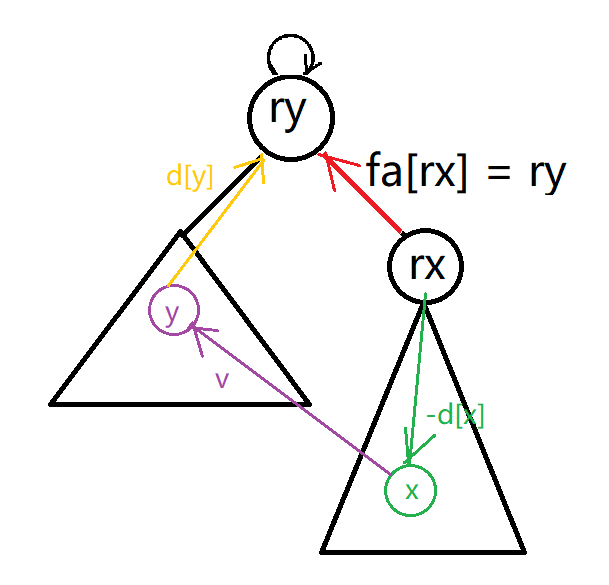
這裡舉的是路徑長度的問題,在遇到各種題目時中可以靈活運用,比如將 \(+\) 改成 \(\times - xor\) 等。
例題
例題5:POJ1703 Find them, Catch them
題目描述
題目翻譯出來有很多種,有說吃糖的,有說警察抓小偷的。。。

思路
一樣的道理,如果一個節點 \(x\) 與父節點的糖的型別相同,那麼關係 \(d[x] = 0\),如果不同 \(d[x] = 1\)。
顯然在 \(find\) 函數中 \(d[x]\) 可以這麼更新: \(d[x] = (d[x] + d[f]) \mod 2\)。
對於第一種操作 D a b ,我們就可以知道 \(a\) 點和 \(b\) 點的關係為 \(1\)。
對於第二種操作 A a b,
首先,如果 \(a\) 和 \(b\) 在不同的集合,我們不能知道它們之間的關係,
否則,\(a\) 和 \(b\) 在相同的集合,我們只要知道 \(a\) 點和 \(b\) 點與根節點的關係是否相同即可,即 \(d[a] - d[b]\) 如果等於 \(0\),那麼 \(a\) 和 \(b\) 型別相同,否則不同。
程式碼
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, m;
int d[N];
int fa[N];
void init() {
for (int i = 0; i <= n; i++) fa[i] = i, d[i] = 0;
}
int find(int x) {
if (x == fa[x]) return x;
int f = fa[x];
fa[x] = find(fa[x]);
d[x] += d[f];
return fa[x];
}
void merge(int x, int y, int v) {
int fx = find(x), fy = find(y);
if (fx == fy) return;
fa[fx] = fy;
d[fx] = -d[x] + v + d[y];
}
int mod(int x, const int m) {
return (x % m + m) % m;
}
void solve() {
scanf("%d%d", &n, &m);
init();
char opt[2];
int a, b;
for (int i = 1; i <= m; i++) {
scanf("%s%d%d", opt, &a, &b);
if (*opt == 'A') {
int fa = find(a), fb = find(b);
if (fa != fb) printf("Not sure yet.\n");
else if (mod(d[a] - d[b], 2) == 0) printf("In the same gang.\n");
else printf("In different gangs.\n");
}
else {
merge(a, b, 1);
}
}
}
int main() {
int T;
scanf("%d", &T);
while (T--) solve();
return 0;
}
例題6:HDU3038 How Many Answers Are Wrong
題目描述

思路
對於一個區間 \([l, r]\) 的和為 \(s\) 我們可以這樣理解:\(l - 1\) 和 \(r\) 的差距為 \(s\)。
我們能想到這一點就非常簡單了,把剛剛的 \(a, b\) 兩點的路徑長度改成 \(l - 1\) 和 \(r\) 相差 \(s\) 即可。
顯然在 \(find\) 函數中 \(d[x]\) 可以這麼更新: \(d[x] = d[x] + d[f]\)。
直接套用模板。
程式碼
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 200010;
int n, m;
int fa[N];
int d[N];
int ans;
void init() {
ans = 0;
for (int i = 0; i <= n; i++) fa[i] = i, d[i] = 0; // 別忘了初始化
}
int find(int u) {
if (u == fa[u]) return u;
int f = fa[u]; // 儲存當前父節點 f,一會要通過 d[f] 更新 d[u]
fa[u] = find(fa[u]); // 路徑壓縮
d[u] += d[f]; // 通過 d[f] 更新 d[u]
return fa[u];
}
void merge(int x, int y, int v) {
int fx = find(x), fy = find(y);
if (fx == fy) { // 在同一個集合,查真偽
if (d[y] - d[x] != v) {
ans++;
}
}
else { // 不在同一個集合,合併以知曉關係
fa[fy] = fx;
d[fy] = -d[y] + v + d[x];
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
while (cin >> n >> m) {
init();
for (int i = 1; i <= m; i++) {
int l, r, s;
cin >> l >> r >> s;
merge(l - 1, r, s); // 注意 l 要 -1
}
cout << ans << '\n';
}
return 0;
}
例題7:P1525 [NOIP2010 提高組] 關押罪犯
題目描述

思路
我們將所有的關係看成邊,所有的犯人看成點,將邊按照怒氣值從大到小排序。
利用貪心,我們從前往後列舉,那麼越靠前的怒氣值越大,我們越不希望將其保留下來,我們更希望將他們放進兩個監獄。
於是我們套路化地將那兩個犯人連上一條權值為 \(1\) 的邊,表示他們最好呆在兩個監獄。
顯然在 \(find\) 函數中 \(d[x]\) 可以這麼更新: \(d[x] = (d[x] + d[f]) \mod 2\)。
即「敵人的敵人是朋友」。
當什麼時候發生矛盾時(比如兩個積怨很深的人不得不在一起時),那麼那個邊的怒氣值就是答案。
程式碼
#include <bits/stdc++.h>
using namespace std;
const int N = 20010, M = 100010;
struct edge {
int u, v, w;
} e[M];
bool cmp(const edge a, const edge b) {
return a.w > b.w;
}
int n, m;
int fa[N];
int d[N];
int mod(int x, const int m) {
return (x % m + m) % m;
}
int find(int x) {
if (x == fa[x]) return x;
int f = fa[x];
fa[x] = find(fa[x]);
d[x] = mod(d[x] + d[f], 2);
return fa[x];
}
bool merge(int x, int y, int v) {
int fx = find(x), fy = find(y);
if (fx == fy) {
if (mod(d[x] - d[y], 2) != v) {
return false;
}
}
else {
fa[fx] = fy;
d[fx] = mod(-d[x] + v + d[y], 2);
}
return true;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= m; i++) cin >> e[i].u >> e[i].v >> e[i].w;
sort(e + 1, e + m + 1, cmp);
for (int i = 1; i <= m; i++) {
if (!merge(e[i].u, e[i].v, 1)) {
cout << e[i].w << '\n';
return 0;
}
}
cout << 0 << '\n';
return 0;
}
例題8:P1196 [NOI2002] 銀河英雄傳說
題目描述

思路
這次權值維護方法的不太一樣。
我們將一列的戰艦當作一個集合,
通過並查集維護集合和每一個點 \(u\) 到根節點的距離 \(dis[u]\),
調查同一個集合的 \(u, v\) 相差多少個戰艦可以通過 \(|dis[u] - dis[v]| - 1\) 算出;
合併 \(x\) 到 \(y\) 時,注意修改 \(dis[x]\) 為 \(y\) 樹原來的大小 \(sz[y]\),然後 \(y\) 樹的大小 \(sz[y]\) 要加上 \(sz[x]\)。
程式碼
#include <bits/stdc++.h>
using namespace std;
const int N = 30010;
int fa[N];
int sz[N];
int d[N];
void init() {
for (int i = 1; i < N; i++) fa[i] = i, sz[i] = 1, d[i] = 0;
}
int find(int x) {
if (x == fa[x]) return x;
int f = fa[x];
fa[x] = find(fa[x]);
d[x] += d[f];
return fa[x];
}
void merge(int x, int y) {
int fx = find(x), fy = find(y);
if (fx == fy) return;
fa[fx] = fy;
d[fx] = sz[fy];
sz[fy] += sz[fx];
}
int query(int x, int y) {
int fx = find(x), fy = find(y);
if (fx != fy) return -1;
return max(0, abs(d[x] - d[y]) - 1);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
init();
int T;
cin >> T;
char opt;
int x, y;
while (T--) {
cin >> opt >> x >> y;
if (opt == 'M') merge(x, y);
else cout << query(x, y) << '\n';
}
return 0;
}