[最長迴文字串]manacher馬拉車

manacher馬拉車 https://www.luogu.com.cn/problem/P3805

閒言一下：花了一箇中午終於把 manacher 給搞懂了。本文將以一個蒟蒻的身份來，來寫寫馬拉車演演算法。首先請自行回顧暴力的 最長迴文字串 演演算法。首先我們將 通過列舉中心點，並擴充套件以該中心點為迴文中心的迴文串長度的演演算法稱為 「中心擴充套件法」。manacher演演算法便是以「中心擴充套件法」為核心，利用列舉中獲取的資訊優化而來的。

具體地來說：

首先在解決奇偶迴文字串時，我們使用分類討論的方法，解決了奇數和偶數的問題，但是這樣未免過於麻煩，有什麼可以將二者統一的方式呢？

這是處理前的字串

這是處理前的字串
a b b c
1 2 3 4


這是處理後的字串
# a # b # b # c #
1 2 3 4 5 6 7 8 9

a b a d a b a 
1 2 3 4 5 6 7

a b b c 
1 2 3 4 

這是處理後的字串 
# a # b # b # c # 
1 2 3 4 5 6 7 8 9 

我們通過加字元的方法，注意這裡不一定要是 # ，也可以是其他字元，主要目標是為了將奇偶迴文字串統一了起來。這樣在處理迴文字串時，會更加的方便。（不過也容易犯一些粗心的小問題，這些問題會在文章末尾提及）。

接下來回想一下 中心擴充套件法 求解最長迴文序列的時候。遇到這種情況時

a b a d a b a 
1 2 3 4 5 6 7

當我們列舉完 以下標為 4 的點為中心時，我們可以知道 1~7 為迴文序列。加上前面以下標為3的點為中心時，我們可知道 1~3 為迴文序列。根據迴文序列的對稱性，我們可以得出 5~7 也為迴文序列。但在我們使用中心擴充套件法時，就需要多餘地去列舉以下標為3的點為中心的迴文半徑的長度。這大大地浪費了時間。因此我們可以從這個角度入手，優化我們的演演算法。

從 中心擴充套件法 的基礎上，再根據剛剛從特殊資料的角度，我們可以想到先定義幾個變數maxr,mid ，用來表示當前已知的迴文序列中最右的右端點，及該回文序列的中點。為什麼要記錄最右的右端點呢？因為右端點越右的迴文序列就越容易包括後面還未遍歷的中心，這樣就能儘可能的達到，通過現有資訊儘可能減少多餘遍歷的目的了。再定義一個陣列 p[i] 表示以 i 為中點的迴文序列的迴文半徑。

具體來講一下優化的要點，

情況一

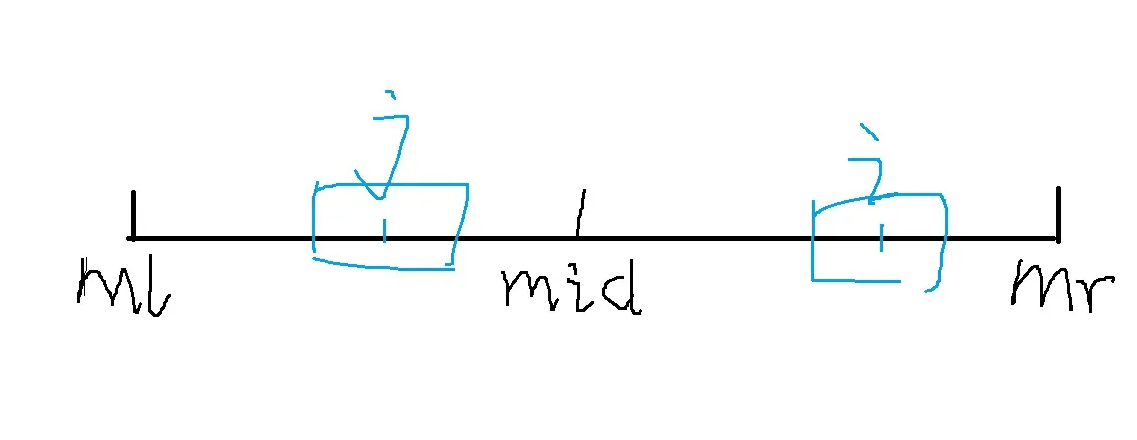
如果是上圖的這種情況，則p[i]=p[j] ， j=mid-(i-mid) --> j=2*mid-i 。（迴文序列的對稱性）

情況二

 

#include<bits/stdc++.h>
using namespace std;
const int N=9*1e7;
string str="!#",c;/*為什麼第一位是「！」？
                    為了避免程式第16行擴充套件時越界 */ 
int p[N],mid=0,mr=0,ans; 
void work(){
    cin>>c; 
    for(int i=0;c[i]>='a'&&c[i]<='z';i++){
        str+=c[i];
        str+='#';
    }/*處理原序列*/ 
    for(int i=1;i<str.size();i++){
        if(i<=mr) p[i]=min(p[2*mid-i],mr-i+1);
        /*i關於mid對稱點; mid-（i-mid）——> 2*mid-i  */ 
        while(str[i-p[i]]==str[i+p[i]]) p[i]++;
        //這裡其實就是擴充套件 迴文序列的 迴文半徑 
        if(i+p[i]>mr){
            mid=i;
            mr=i+p[i]-1; 
        }
        if(p[i]>ans) ans=p[i]; 
    }
    cout<<ans-1;
}
int main(){
    work();
    return 0;
}