【調變解調】ISB 獨立邊帶調幅

說明

學習數位訊號處理演演算法時整理的學習筆記。同系列文章目錄可見 《DSP 學習之路》目錄，程式碼已上傳到 Github - ModulationAndDemodulation。本篇介紹 ISB 獨立邊帶調幅訊號的調變與解調，內附全套 MATLAB 程式碼。

1. ISB 調變演演算法

1.1 演演算法描述

如果發射機仍然發射兩個邊帶，但是和雙邊帶 DSB 訊號不同，兩個邊帶中含有兩種不同的資訊，這種調變方式叫獨立邊帶調變（ISB, Independent Side Band）。ISB 訊號的頻寬等於兩個基頻訊號（調變訊號）頻寬之和，即 \(B_{ISB}={f_{HU}}+{f_{HL}}\)。ISB 訊號的時域表示式為：

式中，\(m_U(t)\) 和 \(m_L(t)\) 分別為上、下邊帶訊號，\(\hat{m}_U(t)\) 和 \(\hat{m}_L(t)\) 分別是上、下邊帶訊號的 Hilbert 變換，推導過程可參考本人同系列文章 【調變解調】SSB 單邊帶調幅。可仿照 SSB 移相法的思路獲得 ISB 訊號。

1.2 ISB 訊號調變範例

調變訊號 \(m(t)\) 可以是確知訊號，也可以是隨機訊號。當 \(m(t)\) 是確知訊號時，不妨假設上邊帶訊號 \(m_U(t)\) 的時域表示式如下：

下邊帶訊號 \(m_L(t)\) 的時域表示式如下：

各調變引數取值：\(f_m=2500Hz\)，\(f_c=20000Hz\)。訊號取樣率 \(f_s=8{f_c}\)，模擬總時長為 \(2s\)。ISB 獨立邊帶調變效果如下圖所示（為了美觀，時域只顯示前 500 個點），上邊帶調變訊號 \(m_U(t)\) 雙邊幅度譜有四根離散譜線（\({\pm}2500Hz\)、\({\pm}1250Hz\)），下邊帶調變訊號 \(m_L(t)\) 雙邊幅度譜有四根離散譜線（\({\pm}3750Hz\)、\({\pm}5000Hz\)），ISB 獨立邊帶訊號有八根離散譜線（\(\pm15000Hz\)、\(\pm16250Hz\)、\(\pm21250Hz\)、\(\pm22500Hz\)）。

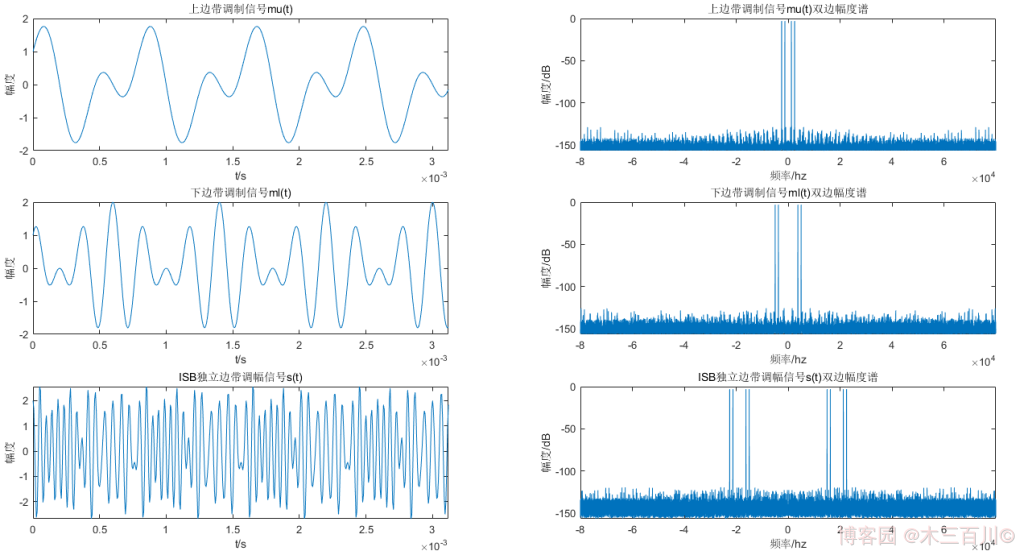
程式碼詳見 mod_isb.m、main_modISB_example.m。

2. ISB 解調演演算法

ISB 訊號解調的相關資料較少，這裡仿照 SSB 訊號數位正交解調的方法做了一個 ISB 訊號數位正交解調。

2.1 數位正交解調

ISB 數位正交解調一般有以下三個步驟：

1. 第一步：乘以正交相干載波得到 \({s_I}(t)\) 與 \({s_Q}(t)\)，即 \({s_I}(t)=s(t)cos({\omega_ct}+{\phi_0})\)，\({s_Q}(t)=-s(t)sin({\omega_ct}+{\phi_0})\)。
2. 第二步：低通濾波器濾除 \({s_I}(t)\) 與 \({s_Q}(t)\) 中的高頻分量。
3. 第三步：計算 \({s_Q}(t)\) 的希爾伯特變換 \(\hat{s}_Q(t)\)，進一步可得上邊帶訊號 \(m_U(t)\) 的解調結果 \(m_{Uo}=s_{I}(t)-\hat{s}_{Q}(t)\)，下邊帶訊號 \(m_L(t)\) 的解調結果 \(m_{Lo}=s_{I}(t)+\hat{s}_{Q}(t)\)。

對 1.2 節中的 ISB 訊號，設定訊雜比 \(SNR=50dB\)，上邊帶解調效果如下，計算誤差，有：\(\sqrt{\sum{{\lvert}m(t_i)-\hat{m}(t_i){\rvert}^2}}/\sqrt{\sum{{\lvert}m(t_i){\rvert}^2}}\approx0.0022\)。

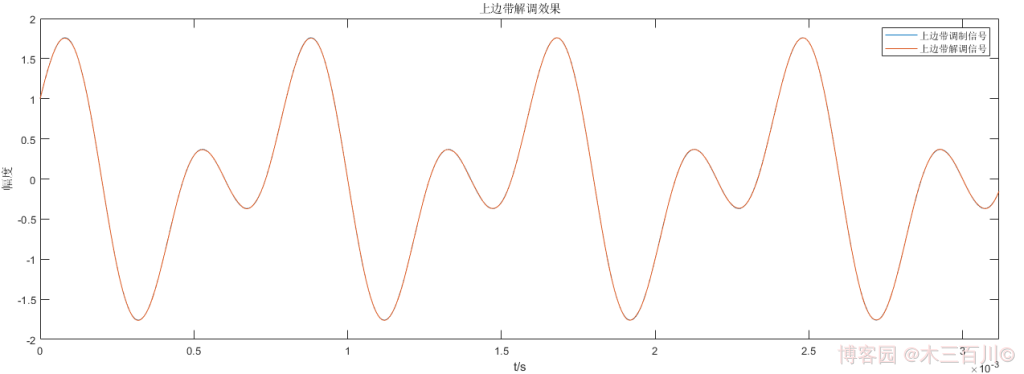
下邊帶解調效果如下，計算誤差，有：\(\sqrt{\sum{{\lvert}m(t_i)-\hat{m}(t_i){\rvert}^2}}/\sqrt{\sum{{\lvert}m(t_i){\rvert}^2}}\approx0.0022\)。

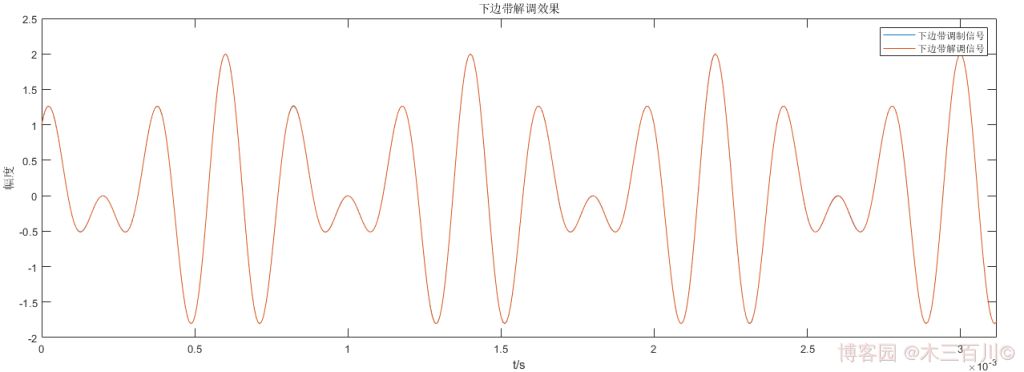
程式碼詳見 demod_isb.m 和 main_demodISB_example.m。更改相干載波的初始相位為 \({\phi_0}=\pi/4,\pi/2\)，或者更改相干載波的中心頻率為 \(0.8f_c,1.2f_c\) 後，解調效果變差，說明這種方法對相干載波同頻同相的要求較高。

參考資料

[1] 樓才義,徐建良,楊小牛.軟體無線電原理與應用[M].電子工業出版社,2014.

附錄程式碼

附.1 檔案 lpf_filter.m

function sig_lpf = lpf_filter(sig_data, cutfre)
% LPF_FILTER    自定義理想低通濾波器
% 輸入引數：
%       sig_data        待濾波資料
%       cutfre          截止頻率，範圍 (0,1)
% 輸出引數：
%       sig_lpf         低通濾波結果
% @author 木三百川

nfft = length(sig_data);
lidx = round(nfft/2-cutfre*nfft/2);
ridx = nfft - lidx;
sig_fft_lpf = fftshift(fft(sig_data));
sig_fft_lpf([1:lidx,ridx:nfft]) = 0;
sig_lpf = real(ifft(fftshift(sig_fft_lpf)));

end

附.2 檔案 mod_isb.m

function [ sig_isb ] = mod_isb(fc, fs, mut, mlt, t)
% MOD_ISB        ISB 獨立邊帶調變
% 輸入引數：
%       fc      載波中心頻率
%       fs      訊號取樣率
%       mut     上邊帶調變訊號
%       mlt     下邊帶調變訊號
%       t       取樣時間
% 輸出引數：
%       sig_isb ISB 獨立邊帶調幅實訊號
% @author 木三百川

% 計算 mu(t) 與 ml(t) 的希爾伯特變換（相移）
hmut = imag(hilbert(mut));
hmlt = imag(hilbert(mlt));

% 與正交載波相合成
sig_isb = (mut+mlt).*cos(2*pi*fc*t)-(hmut-hmlt).*sin(2*pi*fc*t);

% 繪圖
nfft = length(sig_isb);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_isb));
subplot(3,2,1);
plot(t(1:plot_length), mut(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('上邊帶調變訊號mu(t)');
subplot(3,2,2);
plot(freq, 10*log10(fftshift(abs(fft(mut,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('上邊帶調變訊號mu(t)雙邊幅度譜');

subplot(3,2,3);
plot(t(1:plot_length), mlt(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('下邊帶調變訊號ml(t)');
subplot(3,2,4);
plot(freq, 10*log10(fftshift(abs(fft(mlt,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('下邊帶調變訊號ml(t)雙邊幅度譜');

subplot(3,2,5);
plot(t(1:plot_length), sig_isb(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('ISB獨立邊帶調幅訊號s(t)');
subplot(3,2,6);
plot(freq, 10*log10(fftshift(abs(fft(sig_isb,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('ISB獨立邊帶調幅訊號s(t)雙邊幅度譜');

end

附.3 檔案 demod_isb.m

function [ sig_isbu_demod,sig_isbl_demod ] = demod_isb(sig_isb_receive, fc, fs, t, phi0)
% DEMOD_ISB                 ISB 數位正交解調
% 輸入引數：
%       sig_isb_receive     SSB 接收訊號，行向量
%       fc                  載波中心頻率
%       fs                  訊號取樣率
%       t                   取樣時間
%       phi0                載波初始相位
% 輸出引數：
%       sig_isbu_demod      上邊帶解調結果，與 sig_isb_receive 等長
%       sig_isbl_demod      下邊帶解調結果，與 sig_isb_receive 等長
% @author 木三百川

% 第一步：乘以正交相干載波
sig_isb_i = sig_isb_receive.*cos(2*pi*fc*t+phi0);
sig_isb_q = -sig_isb_receive.*sin(2*pi*fc*t+phi0);

% 第二步：低通濾波
sig_isb_i_lpf = lpf_filter(sig_isb_i, fc/(fs/2));
sig_isb_q_lpf = lpf_filter(sig_isb_q, fc/(fs/2));

% 第三步：計算希爾伯特變換
sig_isb_q_lpf = imag(hilbert(sig_isb_q_lpf));
sig_isbu_demod = sig_isb_i_lpf-sig_isb_q_lpf;
sig_isbl_demod = sig_isb_i_lpf+sig_isb_q_lpf;

end

附.4 檔案 main_modISB_example.m

clc;
clear;
close all;
% ISB 調變模擬(調變訊號為確知訊號，相移法)
% @author 木三百川

% 調變引數
fm = 2500;              % 調變訊號引數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 取樣率
total_time = 2;         % 模擬時長，單位：秒

% 取樣時間
t = 0:1/fs:total_time-1/fs;

% 調變訊號為確知訊號
mut = sin(2*pi*fm*t)+cos(pi*fm*t);
mlt = sin(3*pi*fm*t)+cos(4*pi*fm*t);

% ISB 調變
[ sig_isb ] = mod_isb(fc, fs, mut, mlt, t);

附.5 檔案 main_demodISB_example.m

clc;
clear;
close all;
% ISB 解調模擬(調變訊號為確知訊號，數位正交解調)
% @author 木三百川

% 調變引數
fm = 2500;              % 調變訊號引數
fc = 20000;             % 載波頻率
fs = 8*fc;              % 取樣率
total_time = 2;         % 模擬時長，單位：秒

% 取樣時間
t = 0:1/fs:total_time-1/fs;

% 調變訊號為確知訊號
mut = sin(2*pi*fm*t)+cos(pi*fm*t);
mlt = sin(3*pi*fm*t)+cos(4*pi*fm*t);

% ISB 調變
[ sig_isb_send ] = mod_isb(fc, fs, mut, mlt, t);

% 加噪聲
snr = 50;               % 訊雜比
sig_isb_receive = awgn(sig_isb_send, snr, 'measured');

% 數位正交解調
phi0 = 0;
[ sig_isbu_demod,sig_isbl_demod ] = demod_isb(sig_isb_receive, fc, fs, t, phi0);

% 繪圖
nfft = length(sig_isb_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_isb_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_isb_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('ISB接收訊號');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_isb_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('頻率/hz');ylabel('幅度/dB');title('ISB接收訊號雙邊幅度譜');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mut(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_isbu_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('上邊帶解調效果');
legend('上邊帶調變訊號','上邊帶解調訊號');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mlt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_isbl_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('下邊帶解調效果');
legend('下邊帶調變訊號','下邊帶解調訊號');

coefu = mean(abs(mut))/mean(abs(sig_isbu_demod));
fprintf('norm(上邊帶調變訊號 - %.2f * 上邊帶解調訊號)/norm(上邊帶調變訊號) = %.4f.\n', coefu, norm(mut-coefu*sig_isbu_demod)/norm(mut));

coefl = mean(abs(mlt))/mean(abs(sig_isbl_demod));
fprintf('norm(下邊帶調變訊號 - %.2f * 下邊帶解調訊號)/norm(下邊帶調變訊號) = %.4f.\n', coefl, norm(mlt-coefl*sig_isbl_demod)/norm(mlt));