LEA: Improving Sentence Similarity Robustness to Typos Using Lexical Attention Bias 論文閱讀
LEA: Improving Sentence Similarity Robustness to Typos Using Lexical Attention Bias 論文閱讀
KDD 2023 原文地址
Introduction
文字噪聲,如筆誤(Typos), 拼寫錯誤(Misspelling)和縮寫(abbreviations), 會影響基於 Transformer 的模型. 主要表現在兩個方面:
- Transformer 的架構中不使用字元資訊.
- 由噪聲引起的詞元分佈偏移使得相同概念的詞元更加難以關聯.
先前解決噪聲問題的工作主要依賴於資料增強策略, 主要通過在訓練集中加入類似的 typos 和 misspelling 進行訓練.
資料增強確實使得模型在損壞(噪聲)樣本上表現出出更高的魯棒性.
雖然這種策略在一定程度上已被證明有效地緩解了詞元分佈偏移的問題, 但所有這些方法仍然受到在 詞元化(tokenization)中字元資訊會丟失的限制.
Approach
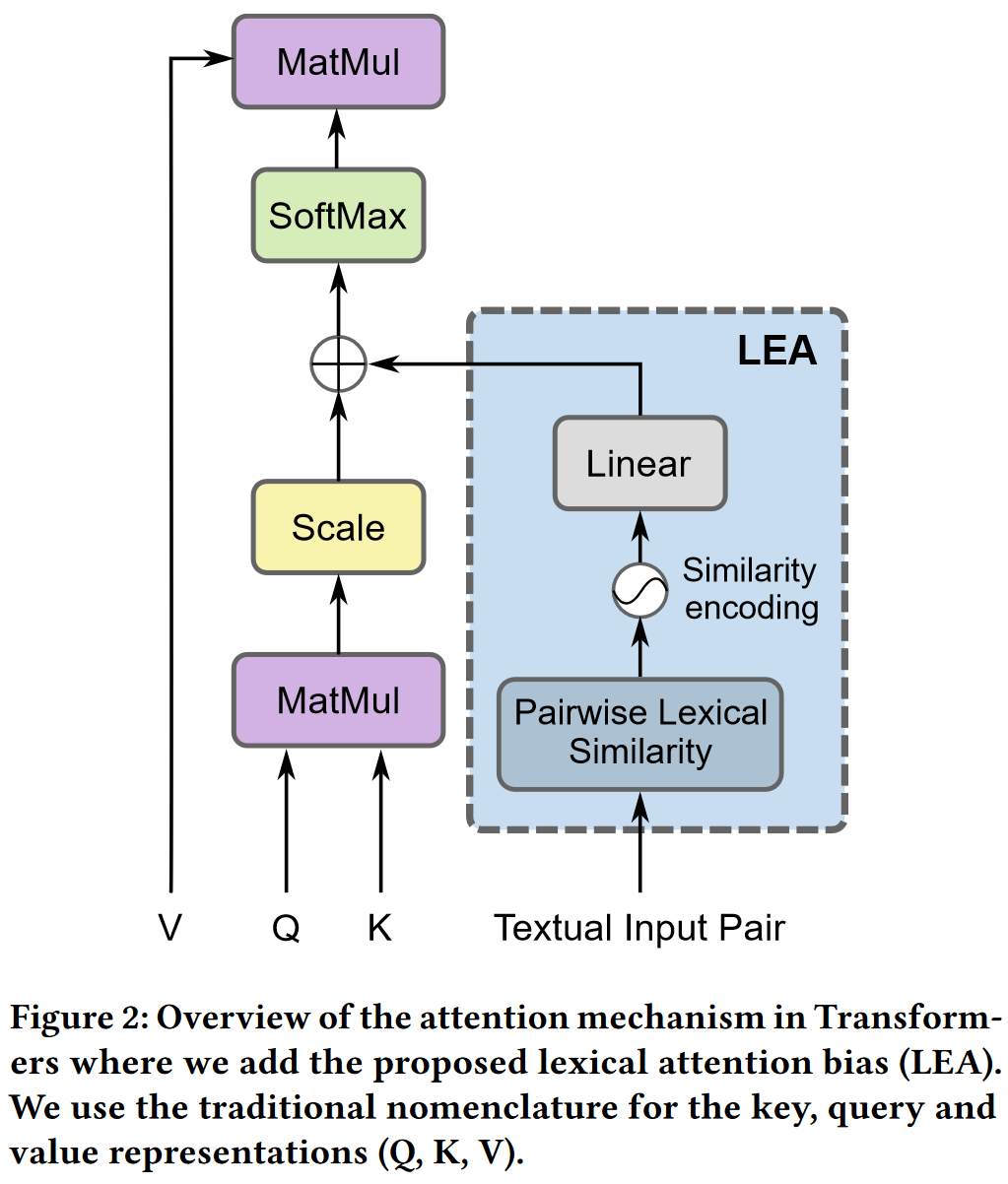
在自注意機制中加入詞感知注意模組(Lexical-aware Attention module, LEA).
LEA 考慮了句子間的詞的字元關係, 文中認為這是提高句子相似性任務的關鍵, 特別是在存在 typos 的情況下.
Self-attention
定義 self-attention 的輸入為 \(X=\set{x_1, x_2, \dots, x_n}\), 輸出為 \(Z=\set{z_1, z_2, \dots, z_n}\), 輸出中的每個 token 的表示計算如下:
其中的注意力權重 \(a_{ij}\) 計算如下:
其中
Lexical attention bias
對於語意文字相似性(textual similarity), 將兩個句子拼接:
主要做法是參考了相對位置嵌入(relative position embeddings)的做法, 對 self-attention 中的 \(e_{ij}\) 進行如下修改:
其中第二項就是詞偏向(lexical bias). \(W^L\in \mathbb R^{d^L\times 1}\) 是可訓練引數, \(l\in \mathbb R^{1\times d^L}\) 是成對詞彙注意嵌入(pairwise lexical attention embedding), \(\alpha\) 是一個固定的比例因子, 它在訓練開始時根據兩個項的大小自動計算一次.
為了計算成對詞彙注意嵌入(pairwise lexical attention embedding), 先計算句子對之間單詞的相似度, 而句子內單詞的相似度設定為0:
其中 Sim 是一個度量, 用於表示兩個單詞之間的字串相似度.
Implementation details
論文中相似度度量選取的是 Jaccard 係數.
只在架構的後半層新增了 lexical attention bias.
之後通過將將 \(s_{ij}\) 帶入 Transformer 中的正餘弦函數, 得到表示詞相似度的 embedding:
最終的詞相似度嵌入 \(l_{ij}\) 是上了兩個向量的拼接.
Experiment
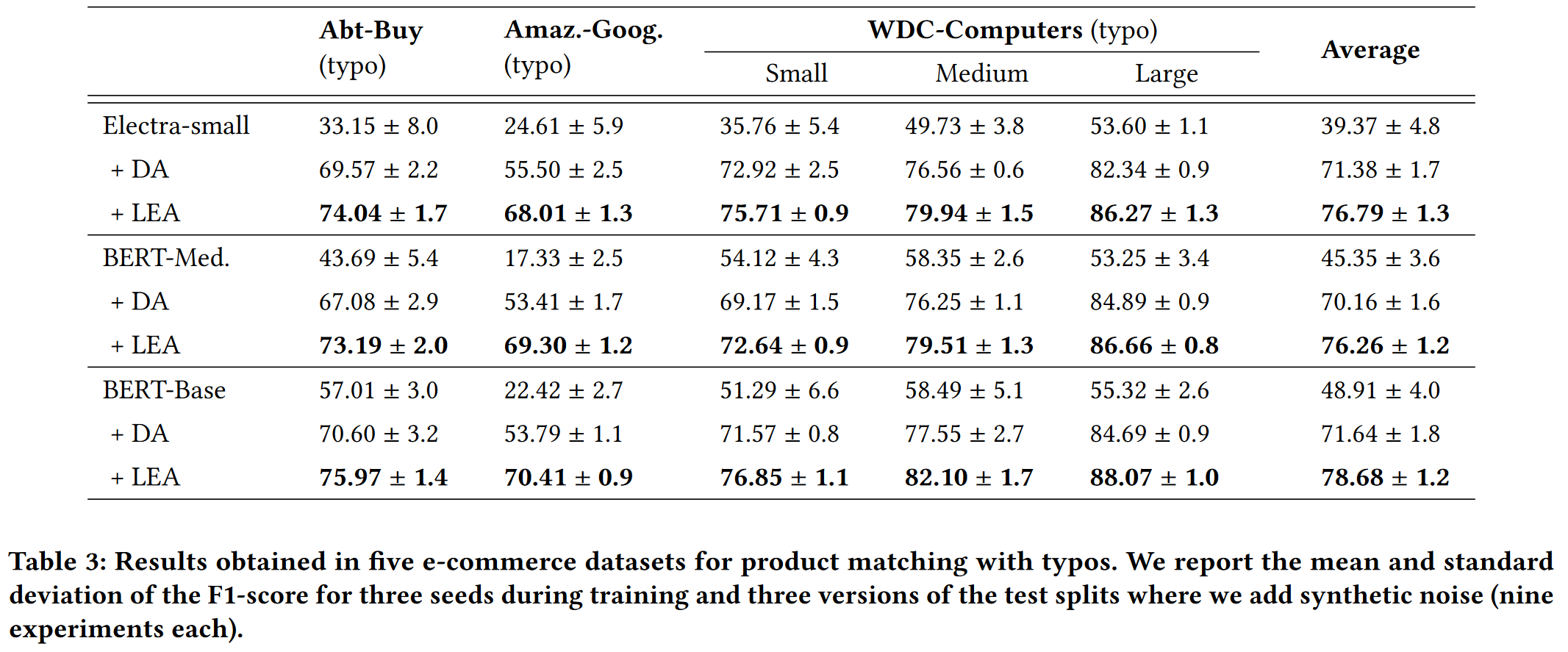
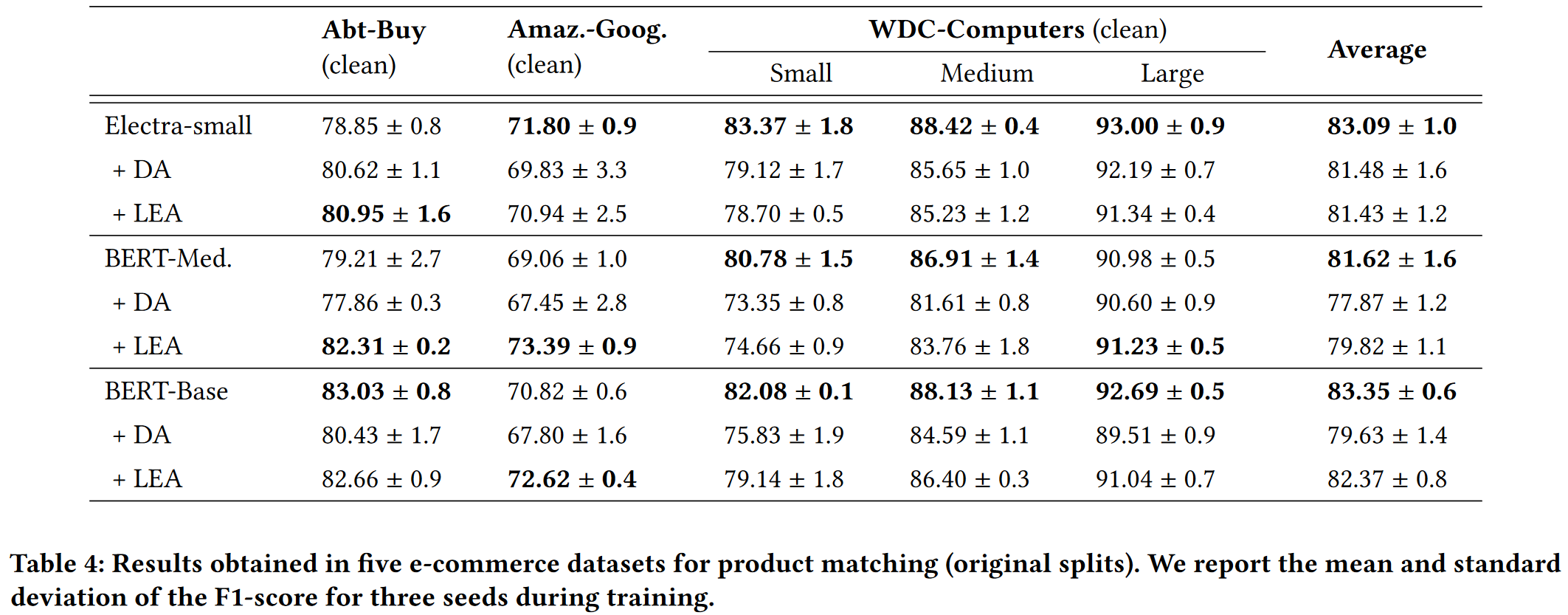
Performance
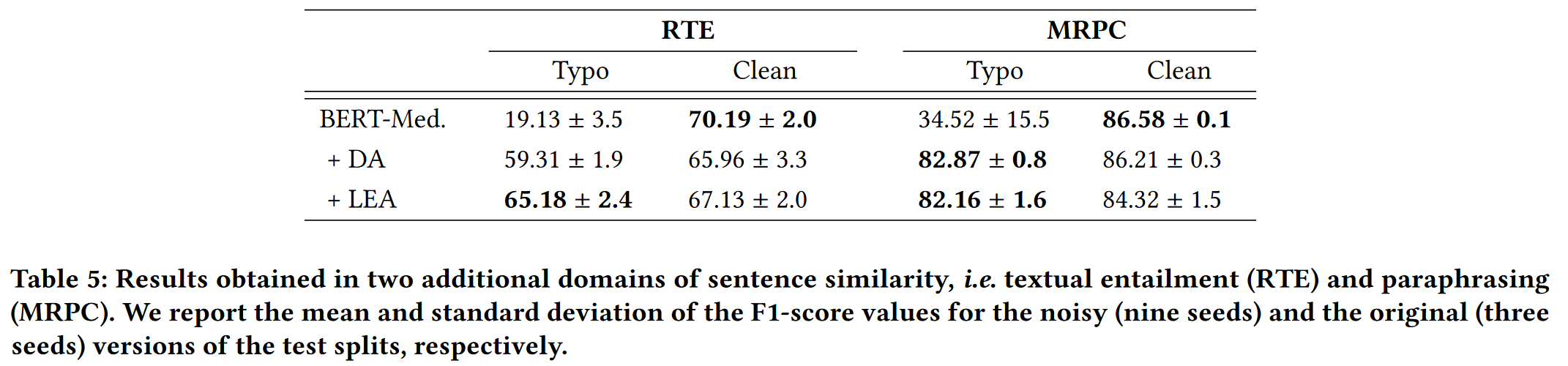
Impact of the lexical similarity choice
分析了使用不同相似度度量在 Abt-Buy 這個資料集上, BERT-Medium 的表現.
相似度度量包括: Jaccard (Jac.), Smith-Waterman (Smith), Longest Common Subsequence (LCS), Levenshtein (Lev.) and Jaro–Winkler (Jaro)

Jaccard 相似度係數是順序不可知的, 因此對字元交換更健壯.
Jaccard 在有錯別字和沒有錯別字的單詞對之間提供了更高的可分離性, 這在短文字中是有益的.
然而, 隨著句子長度的增加, 被比較的單詞具有相似字元但含義不同的概率增加, 這降低了交換不變性優勢.
Jaccard 相似係數: 集合 A, B 的交集與並集的比值
LEA on different layers and sharing strategy
文中認為, LEA 提供的字元級相似性可以被視為一種高階互動資訊.
因此, 它為深層 Transformer 層補充了高層次的特性.
文中並沒有驗證這一假設.
Impact of the noise strength
直觀地說, 由於 LEA 利用的字元級相似性不是在訓練過程中學習到的, 因此它們為模型提供的資訊在某種程度上較少依賴於噪聲的量.
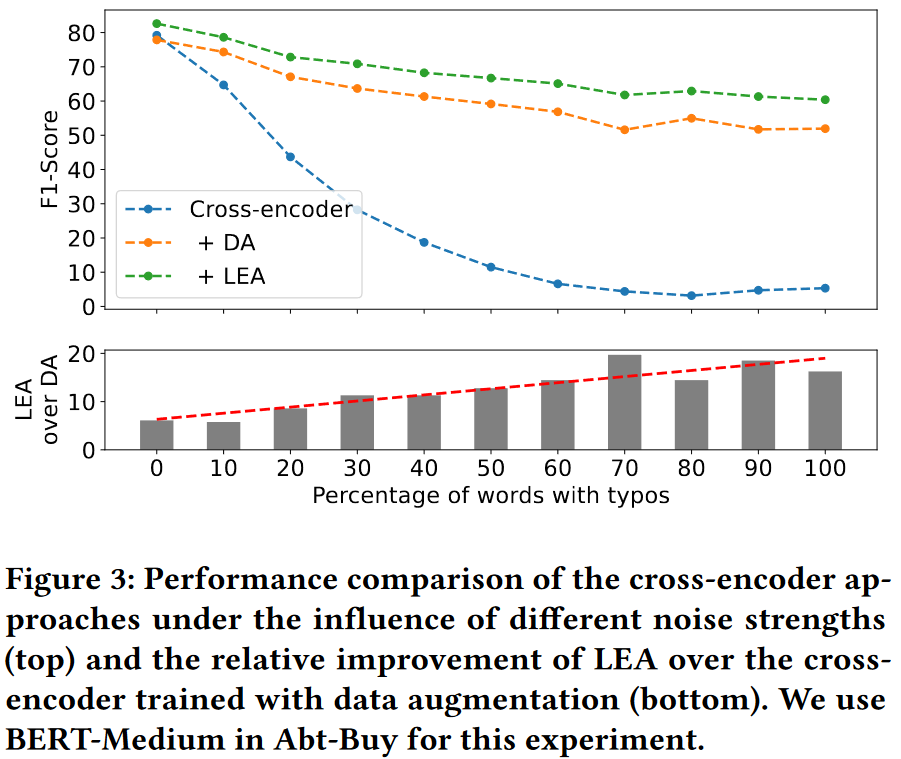
圖3(下)顯示了隨著 typos 數量的增加, LEA 的效能與普通資料增強模型之間的差距越來越大, 這表明 LEA 可以更好地泛化到不同的噪聲強度.
Additional experiments
Larger model
BERT-Large
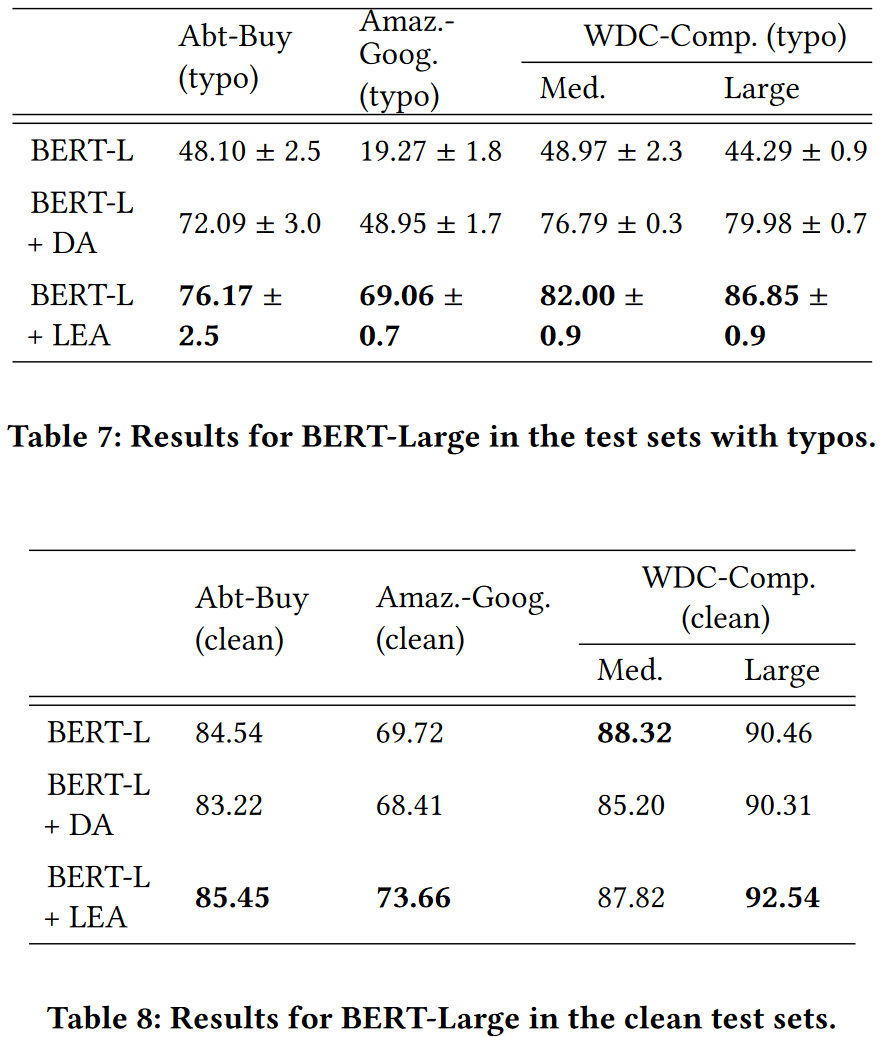
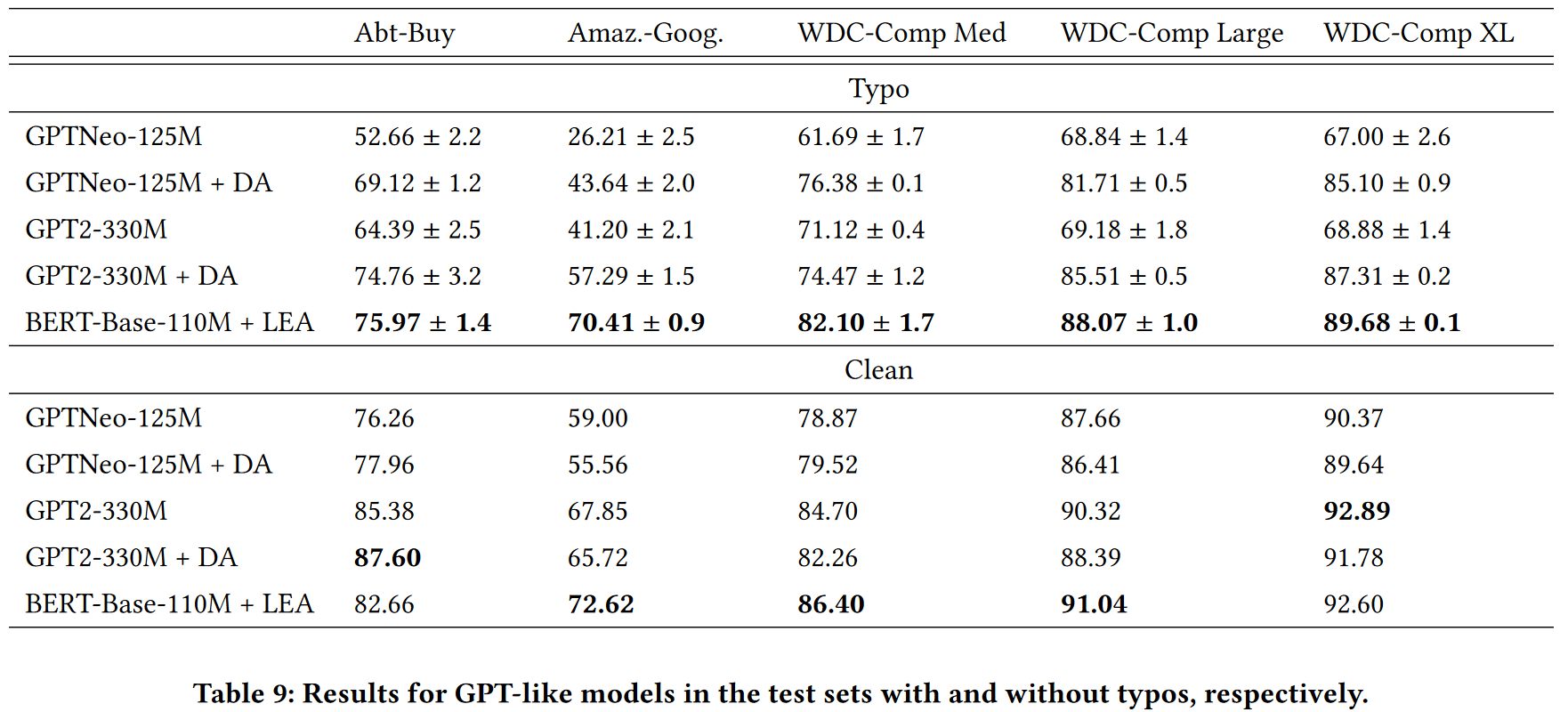
Larger dataset
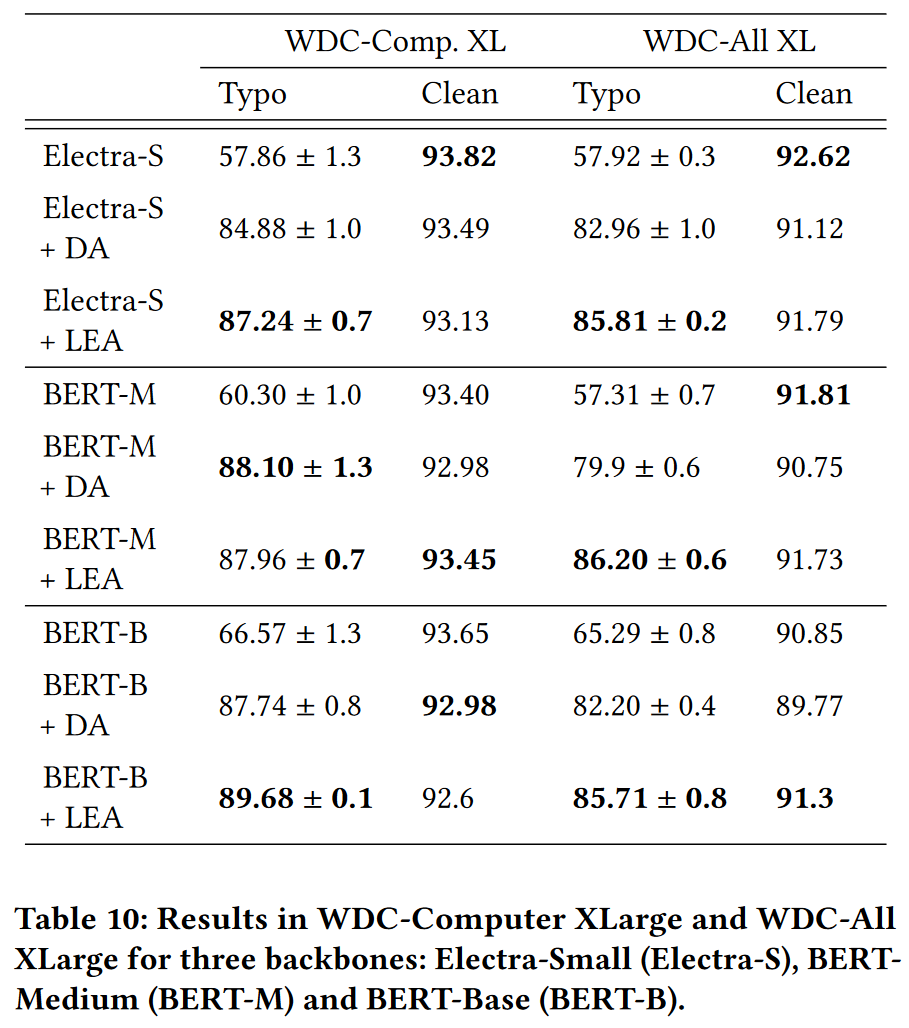
BERT-M + DA 在 WDC-Comp.XL 效能超過了 LEA, 但是標準差較大.