第一部分 按值分裂的 FHQ-Treap

按值分裂的 FHQ-Treap 的典型例題是P3369 【模板】普通平衡樹。

思路

FHQ-Treap 是什麼？

FHQ-Treap 是二元搜尋樹的一種。

比如：

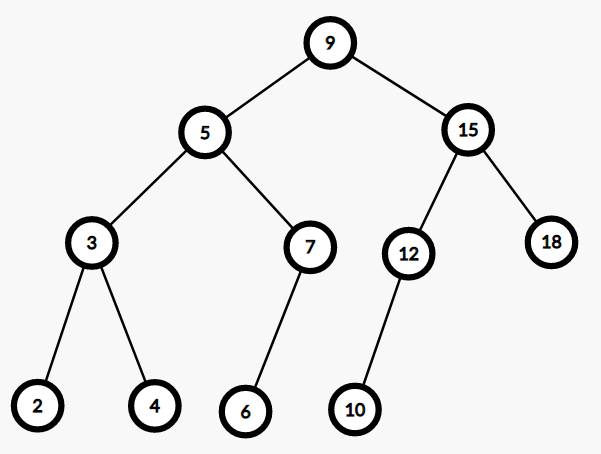
FHQ-Treap 的思想是什麼？

分裂->操作->合併

下面我們就來慢慢講這些操作。

分裂

我們可以根據給定的 \(k\) 將平衡樹分成兩個部分，一部分節點的值都小於等於 \(k\)，一部分節點的值都大於 \(k\)。

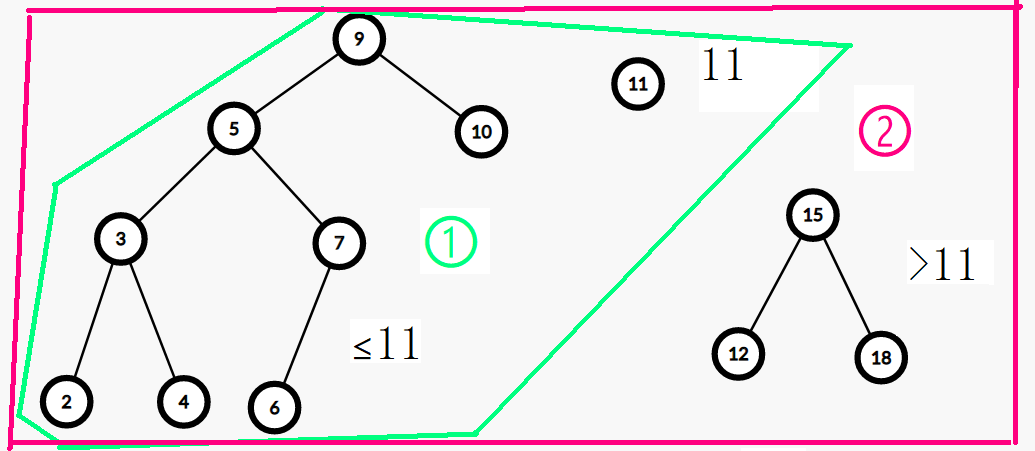
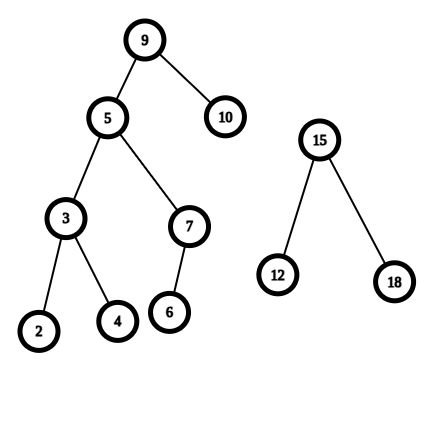
比如 \(k = 10\) 時我們把上圖分成這樣兩個部分：

即：

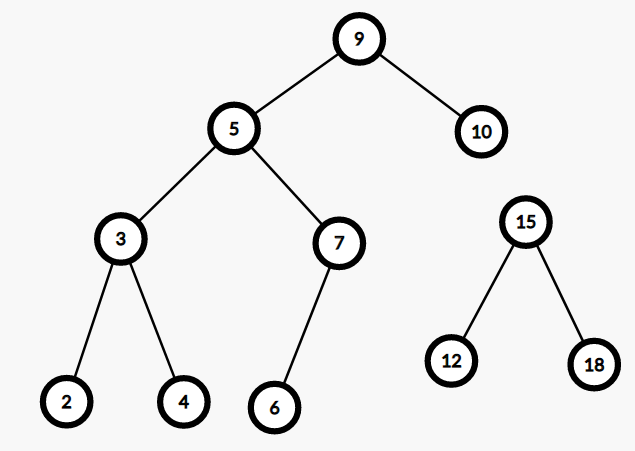
左邊的 \(2, 3, 4, 5, 6, 7, 9, 10\) 都小於等於 \(10\)，右邊的 \(12, 15, 18\) 都大於 \(10\)。

那麼，怎麼讓計算機實現呢？

我們發現圖中的 \(9, 10\) 本不相連，但在分裂後卻是相連的，所以我們並不能討論是否只斷掉某條邊就可以實現分裂。

分裂的過程實際上是在找這個點的過程中完成的：

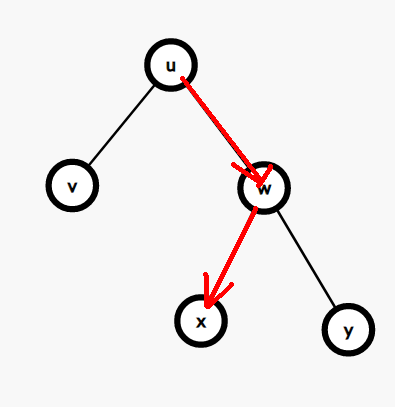
下面我們以分裂出 \(\leq k\) 這部分為例講講怎麼實現分裂。

首先我們發現，當遍歷到一個節點 \(u\)，如果 \(u\) 的值小於等於 \(k\)，我們容易根據二元搜尋樹的性質得出結論：\(u\) 所有的左子樹的值 \(\leq k\)：

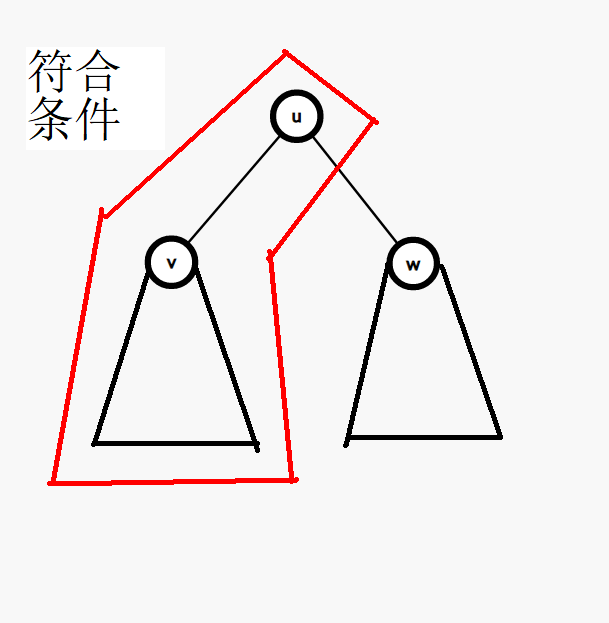
\(u\) 的右子樹的值都不小於 \(u\) 的值，也有可能有 \(\leq k\) 的部分，我們也要把它們（當然也有可能是）連起來。

因為 \(u\) 的右子樹任何一個數值都比 \(u\) 的數值要大，所以從 \(u\) 連向任何右邊的點都是合法的：

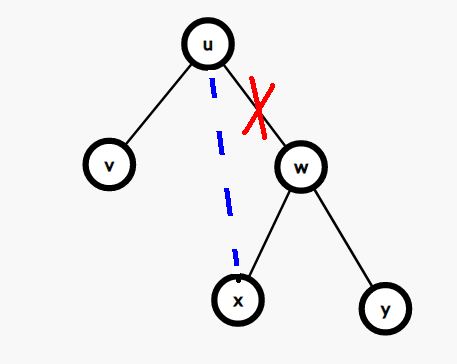
所以當我們在遍歷右子樹的某個點 \(d\) 的時候，如果又出現了 \(d\) 的值 \(\leq k\)，那麼就可以把 \(u\) 的連線右子樹的邊連到 \(d\) 上：

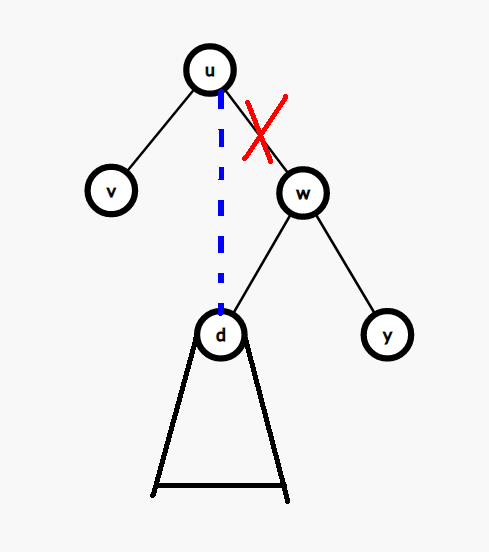
還有一個比較特殊的點，它沒有父節點，那麼它就作為根。

---

以上是處理 \(\leq k\) 的部分的思想，處理 \(> k\) 的方法類似，反著來就行了。

合併

FHQ-Treap 和 普通 Treap 一樣，也分優先順序，維護一個堆的性質。

採用上小下大或上大下小都可以。

合併比分裂容易得多，誰的優先順序高，誰就先上。

插入

分裂：假如要插入 \(k\)，將平衡樹拆分成 \(\leq k\) 和 \(>k\) 兩部分；

新建節點：再新建一個節點，值為 \(k\)；

合併：先合併 \(\leq k\) 的部分和新建節點，然後再與 \(>k\) 的部分合並。

刪除

分裂：假如要刪除 \(k\)，將平衡樹分成 \(<k, =k, >k\) 三個部分。

合併：最後將 \(=k\) 的那個部分的左右子樹合併，再把這三個部分合並就可以了。

查詢一個數的排名

分裂：將平衡樹分裂成 \(\leq (k - 1)\) 和 \(>(k - 1)\) 的兩個部分。

結果：排名就是 \(\leq (k - 1)\) 這一子樹的大小 \(+1\)。

合併：將分裂出來的兩個部分合並。

使用排名來查詢數位

設當前遍歷到點 \(u\)。

1. 如果 \(u\) 的左子樹的大小 \(+1\) 等於排名，那麼結果就是 \(u\) 這個節點的數位；
2. 如果 \(u\) 的左子樹大小大於等於排名，說明結果在左子樹中，那麼遞迴查詢左子樹；
3. 否則遍歷 \(u\) 的右子樹，注意，查詢右子樹時記得將排名減去 \((左子樹的大小 + 1)\)。

找 \(x\) 的前驅

分裂：將平衡樹分成 \(\leq (x - 1)\) 和 \(>(x - 1)\) 的兩個部分

結果：使用上面的「使用排名來查詢數位」的方法求出 \(\leq (x - 1)\) 部分的平衡樹的最大的一個數。

合併：將分裂出來的兩個部分合並。

找 \(x\) 的後繼

分裂：將平衡樹分成 \(\leq x\) 和 \(>x\) 的兩個部分

結果：使用上面的「使用排名來查詢數位」的方法求出 \(>x\) 部分的平衡樹的最小的一個數。

合併：將分裂出來的兩個部分合並。

例題程式碼

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

struct node {
	int l, r;
	int size;
	int rnd;
	int key;
} tr[N];

int root, idx;

void pushup(int u) {
	tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + 1;
}

int newnode(int key) {
	idx++;
	tr[idx].key = key;
	tr[idx].rnd = rand();
	tr[idx].size = 1;
	tr[idx].l = tr[idx].r = 0;
	return idx;
}

void split(int u, int key, int &x, int &y) {
	if (!u) {
		x = y = 0;
		return;
	}
	if (tr[u].key <= key) {
		x = u;
		split(tr[u].r, key, tr[u].r, y);
	}
	else {
		y = u;
		split(tr[u].l, key, x, tr[u].l);
	}
	pushup(u);
}

int merge(int x, int y) {
	if ((!x) || (!y)) return x | y;
	if (tr[x].rnd < tr[y].rnd) {
		tr[x].r = merge(tr[x].r, y);
		pushup(x);
		return x;
	} 
	else {
		tr[y].l = merge(x, tr[y].l);
		pushup(y);
		return y;
	}
}

void insert(int key) {
	int x, y, z;
	split(root, key, x, y);
	z = newnode(key);
	root = merge(merge(x, z), y);
}

void del(int key) {
	int x, y, z;
	split(root, key, x, y);
	split(x, key - 1, x, z);
	z = merge(tr[z].l, tr[z].r);
	root = merge(merge(x, z), y);
}

int get_rank_by_key(int key) {
	int x, y, z;
	split(root, key - 1, x, y);
	int ans = tr[x].size + 1;
	root = merge(x, y);
	return ans;
}

int get_key_by_rank(int u, int rk) {
	if (tr[tr[u].l].size + 1 == rk) return tr[u].key;
	else if (tr[tr[u].l].size >= rk) return get_key_by_rank(tr[u].l, rk);
	else return get_key_by_rank(tr[u].r, rk - tr[tr[u].l].size - 1);
}

int get_pre(int key) {
	int x, y, z;
	split(root, key - 1, x, y);
	int ans = get_key_by_rank(x, tr[x].size);
	root = merge(x, y);
	return ans;
}

int get_nxt(int key) {
	int x, y, z;
	split(root, key, x, y);
	int ans = get_key_by_rank(y, 1);
	root = merge(x, y);
	return ans;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int T;
	cin >> T;
	int opt, x;
	while (T--) {
		cin >> opt >> x;
		if (opt == 1) insert(x);
		else if (opt == 2) del(x);
		else if (opt == 3) cout << get_rank_by_key(x) << '\n';
		else if (opt == 4) cout << get_key_by_rank(root, x) << '\n';
		else if (opt == 5) cout << get_pre(x) << '\n';
		else cout << get_nxt(x) << '\n';
	}
	return 0;
}

第二部分 按大小（\(size\)）分裂的 FHQ-Treap

按大小分裂的 FHQ-Treap 的典型例題是P3391 【模板】文藝平衡樹。

思路

在所有操作中，除了分裂操作以外，都是一樣的。

只有分裂操作與按值分裂的不同，比較的物件是大小：

原圖：

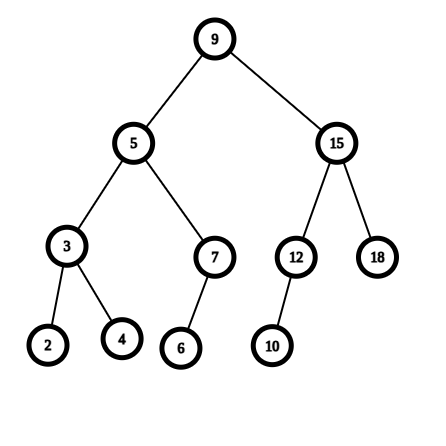
操作：

結果：

例題程式碼

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

struct node {
    int l, r;
    int sz;
    int key;
    int rnd;
    int tag;
} tr[N];

int root, idx;

void pushup(int u) {
    tr[u].sz = tr[tr[u].l].sz + tr[tr[u].r].sz + 1;
}

int newnode(int key) {
    idx++;
    tr[idx].key = key;
    tr[idx].rnd = rand();
    tr[idx].tag = 0;
    tr[idx].l = tr[idx].r = 0;
    tr[idx].sz = 1;
    return idx;
}

void pushdown(int u) {
    if (tr[u].tag) {
        tr[tr[u].l].tag ^= 1;
        tr[tr[u].r].tag ^= 1;
        swap(tr[u].l, tr[u].r);
        tr[u].tag = 0;
    }
}

void split(int u, int sz, int &x, int &y) {
    if (!u) {
        x = y = 0;
        return;
    }
    pushdown(u);
    if (tr[tr[u].l].sz + 1 <= sz) {
        x = u;
        split(tr[u].r, sz - tr[tr[u].l].sz - 1, tr[u].r, y);
    }
    else {
        y = u;
        split(tr[u].l, sz, x, tr[u].l);
    }
    pushup(u);
}

int merge(int x, int y) {
    if ((!x) || (!y)) return x | y;
    if (tr[x].rnd > tr[y].rnd) {
        pushdown(x);
        tr[x].r = merge(tr[x].r, y);
        pushup(x);
        return x;
    }
    else {
        pushdown(y);
        tr[y].l = merge(x, tr[y].l);
        pushup(y);
        return y;
    }
}

void insert(int p, int key) {
    int x, y, z;
    split(root, p - 1, x, y);
    z = newnode(key);
    root = merge(merge(x, z), y);
}

void reverse_arr(int l, int r) {
    int x, y, z;
    split(root, r, x, z);
    split(x, l - 1, x, y);
    tr[y].tag ^= 1;
    root = merge(merge(x, y), z);
}

void dfs(int u) {
    if (!u) return;
    pushdown(u);
    dfs(tr[u].l);
    cout << tr[u].key << ' ';
    dfs(tr[u].r);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, T;
    cin >> n >> T;
    for (int i = 1; i <= n; i++) insert(i, i);
    while (T--) {
        int l, r;
        cin >> l >> r;
        reverse_arr(l, r);
    }

    dfs(root);

    return 0;
}

第三部分 練習

P4008 [NOI2003] 文字編輯器

題目描述

思路

文藝平衡樹的基本運用。

程式碼

#include <bits/stdc++.h>

using namespace std;

const int N = 3200000;

struct node {
    int l, r;
    int size;
    char key;
    int rnd;
} tr[N];

int root, idx;

int newnode(char key) {
    idx++;
    tr[idx].key = key;
    tr[idx].rnd = rand();
    tr[idx].size = 1;
    tr[idx].l = tr[idx].r = 0;
    return idx;
}

void pushup(int u) {
    tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + 1;
}

void split(int u, int sz, int &x, int &y) {
    if (!u) {
        x = y = 0;
        return;
    }
    if (tr[tr[u].l].size + 1 <= sz) {
        x = u;
        split(tr[u].r, sz - tr[tr[u].l].size - 1, tr[u].r, y);
    }
    else {
        y = u;
        split(tr[u].l, sz, x, tr[u].l);
    }
    pushup(u);
}

int merge(int x, int y) {
    if ((!x) || (!y)) return x | y;
    if (tr[x].rnd < tr[y].rnd) {
        tr[x].r = merge(tr[x].r, y);
        pushup(x);
        return x;
    }
    else {
        tr[y].l = merge(x, tr[y].l);
        pushup(y);
        return y;
    }
}

int p;

void insert(int sz) {
    int x, y, z = 0, s;
    split(root, p, x, y);
    char ch = 0;
    for (int i = 1; i <= sz; i++) {
        ch = getchar();
        if (ch == '\n' || ch == '\r') {
            i--;
            continue;
        }
        s = newnode(ch);
        if (!z) z = s;
        else z = merge(z, s);
    }
    root = merge(merge(x, z), y);
}

void del(int sz) {
    int x, y, z;
    if (!p) {
        split(root, sz, x, y);
        root = y;
        return;
    }
    split(root, p + sz, x, z);
    split(x, p, x, y);
    root = merge(x, z);
}

void output(int u) {
    if (!u) return;
    output(tr[u].l);
    putchar(tr[u].key);
    output(tr[u].r);
}

void print(int sz) {
    int x, y, z;
    split(root, p + sz, x, z);
    split(x, p, x, y);
    output(y);
    root = merge(merge(x, y), z);
    putchar('\n');
}

int main() {
    int T;
    char opt[10];
    scanf("%d", &T);

    while (T--) {
        scanf("%s", opt);
        if (opt[0] == 'M') scanf("%d", &p);
        else if (opt[0] == 'I') {
            int sz;
            scanf("%d", &sz);
            insert(sz);
        }
        else if (opt[0] == 'D') {
            int sz;
            scanf("%d", &sz);
            del(sz);
        }
        else if (opt[0] == 'G') {
            int sz;
            scanf("%d", &sz);
            print(sz);
        }
        else if (opt[0] == 'P') p--;
        else p++;
        // output(root);
        // cout << endl;
    }
    return 0;
}

P2596 [ZJOI2006] 書架

題目描述

思路

對每一種操作，

對 FHQ-Treap 樹按要求進行分裂，

再用不同的順序進行合併，

就實現了題目中的各種調換。

是練習分裂的絕佳好題。

程式碼

#include <bits/stdc++.h>

using namespace std;

const int N = 90010;

struct node {
    int l, r;
    int size;
    int key;
    int rnd;
    int fa;
} tr[N];

int root, idx;
int st[N];

int newnode(int key, int fa) {
    idx++;
    st[key] = idx;
    tr[idx].key = key;
    tr[idx].fa = fa;
    tr[idx].rnd = rand();
    tr[idx].size = 1;
    tr[idx].l = tr[idx].r = 0;
    return idx;
}

void pushup(int u) {
    tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + 1;
    if (tr[u].l) tr[tr[u].l].fa = u;
    if (tr[u].r) tr[tr[u].r].fa = u;
}

void split(int u, int sz, int &x, int &y) {
    if (!u) {
        x = y = 0;
        return;
    }
    if (tr[tr[u].l].size + 1 <= sz) {
        x = u;
        split(tr[u].r, sz - tr[tr[u].l].size - 1, tr[u].r, y);
    }
    else {
        y = u;
        split(tr[u].l, sz, x, tr[u].l);
    }
    pushup(u);
}

int merge(int x, int y) {
    if ((!x) || (!y)) return x | y;
    if (tr[x].rnd < tr[y].rnd) {
        tr[x].r = merge(tr[x].r, y);
        pushup(x);
        return x;
    }
    else {
        tr[y].l = merge(x, tr[y].l);
        pushup(y);
        return y;
    }
}

int get_rank(int ver, int rt) {
    int rk = tr[tr[ver].l].size;
    while (ver != rt) {
        int fa = tr[ver].fa;
        if (tr[fa].r == ver) rk += tr[tr[fa].l].size + 1;
        ver = fa;
    }
    return rk + 1;
}

void insert(int p, int key) {
    int x, y, z;
    split(root, p - 1, x, y);
    z = newnode(key, 0);
    root = merge(merge(x, z), y);
}

void top(int s) {
    int p = get_rank(st[s], root);
    int x, y, z;
    split(root, p, x, z);
    split(x, p - 1, x, y);
    root = merge(merge(y, x), z);
}

void bottom(int s) {
    int p = get_rank(st[s], root);
    int x, y, z;
    split(root, p, x, z);
    split(x, p - 1, x, y);
    root = merge(merge(x, z), y);
}

void change(int s, int t) {
    if (!t) return;
    int p = get_rank(st[s], root);
    int x, y, z, l, r;
    if (t > 0) {
        split(root, p + 1, x, l);
        split(x, p, x, z);
        split(x, p - 1, x, y);
    }
    else {
        split(root, p, x, l);
        split(x, p - 1, x, z);
        split(x, p - 2, x, y);
    }
    root = merge(x, merge(z, merge(y, l)));
}

int ask(int p) {
    return get_rank(st[p], root);
}

int query(int p) {
    int x, y, z;
    split(root, p, x, z);
    split(x, p - 1, x, y);
    int ans = tr[y].key;
    root = merge(merge(x, y), z);
    return ans;
}

int n, m;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        insert(i, x);
    }

    char opt[10];
    int t1, t2;
    while (m--) {
        cin >> opt;
        if (opt[0] == 'T') {
            cin >> t1;
            top(t1);
        }
        else if (opt[0] == 'B') {
            cin >> t1;
            bottom(t1);
        }
        else if (opt[0] == 'I') {
            cin >> t1 >> t2;
            change(t1, t2);
        }
        else if (opt[0] == 'A') {
            cin >> t1;
            cout << ask(t1) - 1 << '\n';
        }
        else if (opt[0] == 'Q') {
            cin >> t1;
            cout << query(t1) << '\n';
        }
    }
    return 0;
}