編碼技巧 --- 如何實現字串運算表示式的計算

引言

最近做一個設定的功能，需求是該設定項跟另一個整形設定項關聯，具有一定的函數關係，例如有一個設定項是值為 N ，則另一設定 F 項滿足函數關係\(F=2/(N+1)\)。這個函數關係是客戶手動輸入，只需要簡單的四則運算，所以我們要做的就是判斷四則運算表示式是否有效，且給定 N 的值，算出表示式的值。

如何快速判斷一個四則運算公式字串是否符合規則，且根據給定值計算出該公式的值？

雙棧實現

實際上編譯器就是利用了雙棧實現了的表示式求值，其中一個棧用來儲存運算元，另一個棧用來儲存運運算元。

從左向右遍歷表示式，當遇到數位時，就將其直接壓入運算元棧；當遇到運運算元時，就將其與運運算元棧的棧頂元素比較。

如果遇到的運運算元比運運算元棧頂的元素的優先順序高，就將這個運運算元壓入棧；

如果遇到的運運算元比運運算元棧頂的元素的優先順序低或兩者相同，就從運運算元棧頂取出運運算元，在從運算元棧頂取兩個運算元，然後進行計算，並把計算的得到的結果壓入運算元棧，繼續比較這個運運算元與運運算元棧頂的元素；

下圖表示一個簡單四則運算表示式 3+5*8-6的計算過程：

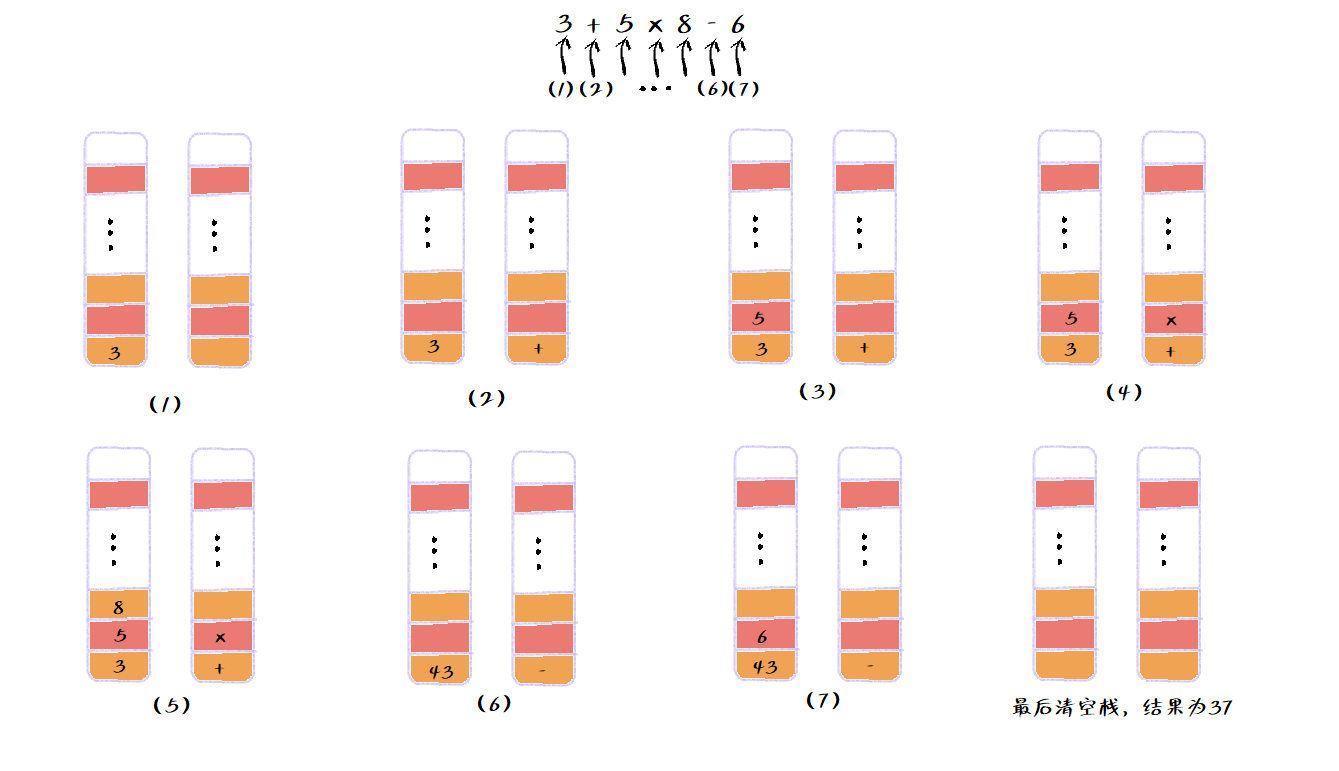
程式碼實現可以大概簡化可以分為以下步驟：

定義運運算元棧 operatorStack 和運算元棧 operandStack 。
從左至右掃描表示式,遇到運算元時,直接將其推入運算元棧 operandStack 。
遇到運運算元時,比較其與運運算元棧頂部運運算元的優先順序:
- 如果該運運算元的優先順序高於或等於運運算元棧頂部運運算元,則將該運運算元直接入棧 operatorStack 。
- 如果該運運算元的優先順序低於運運算元棧頂部運運算元,則將運運算元棧頂部的運運算元出棧,從運算元棧中彈出兩個運算元,計算結果後再入棧 operandStack ,重複此步驟直到運運算元棧為空或遇到優先順序高於或等於該運運算元的棧頂運運算元為止。
遇到括號時:
- 如果是左括號「(」,則直接入棧 operatorStack 。
- 如果是右括號「)」,則將運運算元棧棧頂的運運算元出棧,從運算元棧中彈出兩個運算元計算結果,重複此步驟直到遇到左括號為止,並將這一對括號從運運算元棧中移除。
重複步驟3和4,直到表示式的最右端。
將運運算元棧中剩餘的所有運運算元依次出棧,從運算元棧中彈出兩個運算元,計算結果後入棧operandStack。
運算元棧最終只剩一個運算元,這就是表示式的計算結果。

具體實現程式碼如下：

class ExpressionEvaluator
{
    static Dictionary<char, int> PrecedenceDic = new Dictionary<char, int> {
            {'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}, {'^', 3}
        };

    static Dictionary<char, Func<int, int, int>> OperatorsDic = new Dictionary<char, Func<int, int, int>> {
            {'+', (a, b) => a + b },
            {'-', (a, b) => a - b },
            {'*', (a, b) => a * b },
            {'/', (a, b) => a / b },
            {'^', (a, b) => (int)Math.Pow(a, b)}
        };

    public static bool EvaluateExpression(string expression, out double result)
    {
        result = 0;
        try
        {
            // 使用正規表示式驗證四則運算表示式的有效性
            string pattern = @"^[-+*/^() x\d\s]+$";

            if (!Regex.IsMatch(expression, pattern))
            {
                return false;
            }
            //操作符棧
            Stack<char> operatorStack = new Stack<char>();
            //運算元棧
            Stack<int> operandStack = new Stack<int>();

            for (int i = 0; i < expression.Length; i++)
            {
                char c = expression[i];

                if (c == ' ') continue;

                if (char.IsDigit(c))
                {
                    //獲取運算元
                    int operand = 0;
                    while (i < expression.Length && char.IsDigit(expression[i]))
                    {
                        operand = operand * 10 + (expression[i++] - '0');
                    }
                    i--;
                    operandStack.Push(operand);
                }
                else if (OperatorsDic.ContainsKey(c))
                {
                    while (operatorStack.Count > 0 &&
                        OperatorsDic[c] != null && operatorStack.Peek() != '(' &&
                        PrecedenceDic[operatorStack.Peek()] >= PrecedenceDic[c])
                    {
                        int b = operandStack.Pop();
                        int a = operandStack.Pop();
                        operandStack.Push(OperatorsDic[operatorStack.Pop()](a, b));
                    }
                    operatorStack.Push(c);
                }
                else if (c == '(')
                {
                    operatorStack.Push(c);
                }
                else if (c == ')')
                {
                    while (operatorStack.Peek() != '(')
                    {
                        int b = operandStack.Pop();
                        int a = operandStack.Pop();
                        operandStack.Push(OperatorsDic[operatorStack.Pop()](a, b));
                    }
                    operatorStack.Pop();
                }
            }

            while (operatorStack.Count > 0)
            {
                int b = operandStack.Pop();
                int a = operandStack.Pop();
                operandStack.Push(OperatorsDic[operatorStack.Pop()](a, b));
            }
            result = operandStack.Pop();

            return true;
        }
        catch (Exception)
        {
            return false;
        }
    }
}

那接下來測試一下程式碼，因為程式碼內只做了整形的計算，所以表示式也只用整形。

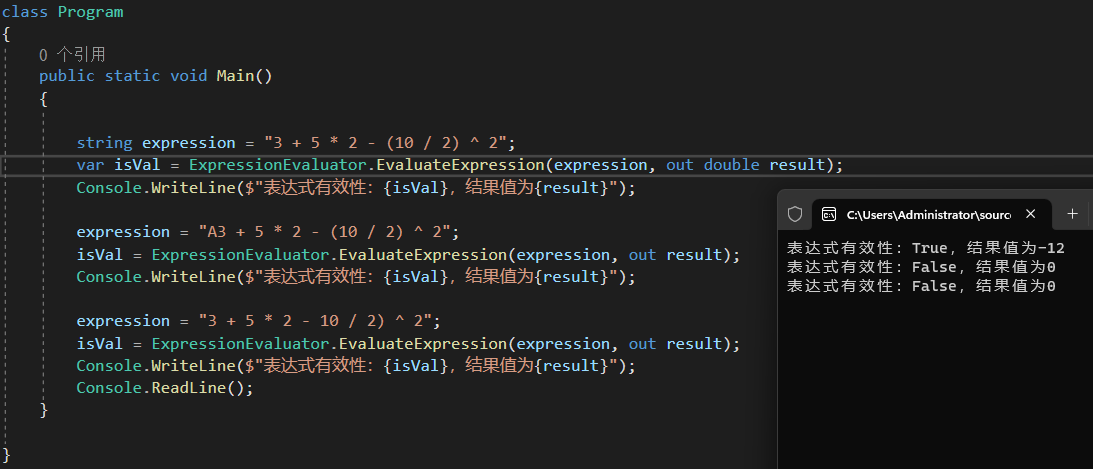
官方API

實際上微軟官方在 System.Data 庫中 DataTable.Compute(String, String)方法實現了計算表示式，程式碼如下

using System;
using System.Data;
using System.Text.RegularExpressions;

public class ArithmeticExpressionEvaluator
{
    public static bool IsArithmeticExpression(int arg, string str, out double result)
    {
        result = 0;

        // 驗證字串是否包含有效的四則運算表示式
        if (!IsValidArithmeticExpression(str) || !str.ToLower().Contains("x".ToLower()))
        {
            return false;
        }

        // 將字串中的變數x替換為傳入的整數arg
        string expression = str.Replace("x", arg.ToString());

        // 計算並返回表示式的值
        try
        {
            return double.TryParse(new DataTable().Compute(expression, "").ToString(), out result);
        }
        catch
        {
            return false;
        }
    }

    private static bool IsValidArithmeticExpression(string str)
    {
        // 使用正規表示式驗證四則運算表示式的有效性
        string pattern = @"^[-+*/() x\d\s]+$";
        return Regex.IsMatch(str, pattern);
    }
}
class Program
{
    public static void Main()
    {
        while (true)
        {
            string expression = Console.ReadLine();
            string arg = Console.ReadLine();

            if (ArithmeticExpressionEvaluator.IsArithmeticExpression(int.Parse(arg), expression, out double result))
            {
                Console.WriteLine($"The result of the arithmetic expression is: {result}");
            }
            else
            {
                Console.WriteLine("The input string is not a valid arithmetic expression.");
            }
        }
    }
}

測試結果：

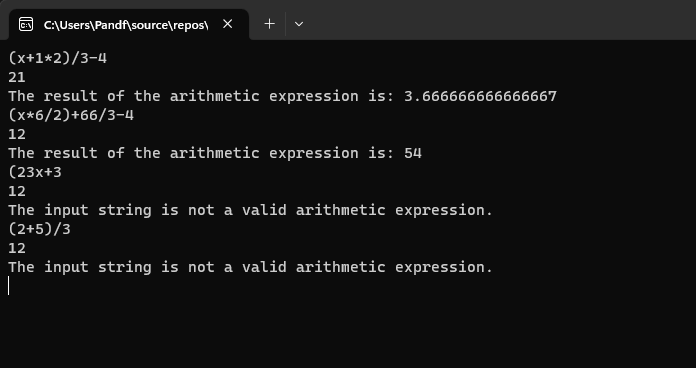
總結

剛開始拿到這個需求還是有點頭疼的，想了很久的方案，突然想到之前看資料結構的書的時候，提到過棧在表示式求值中的應用，翻書看了一下，還是被這個實現方案驚豔到了，所以，還是需要多讀多看多思考，才能在面對各種需求遊刃有餘，加油~