「學習筆記」字尾陣列

感謝 LB 學長的博文！

前置知識

字尾是指從某個位置 \(i\) 開始到整個串末尾結束的一個特殊子串，也就是 \(S[i \dots|S|-1]\)。

計數排序 - OI Wiki (oi-wiki.org)

基數排序 - OI Wiki (oi-wiki.org)

變數

字尾陣列最主要的兩個陣列是 sa 和 rk。

sa 表示將所有字尾排序後第 \(i\) 小的字尾的編號，即編號陣列。

rk 表示字尾 \(i\) 的排名，即排名陣列。

這兩個陣列滿足一個重要性質： sa[rk[i]] = rk[sa[i]] = i。

範例：

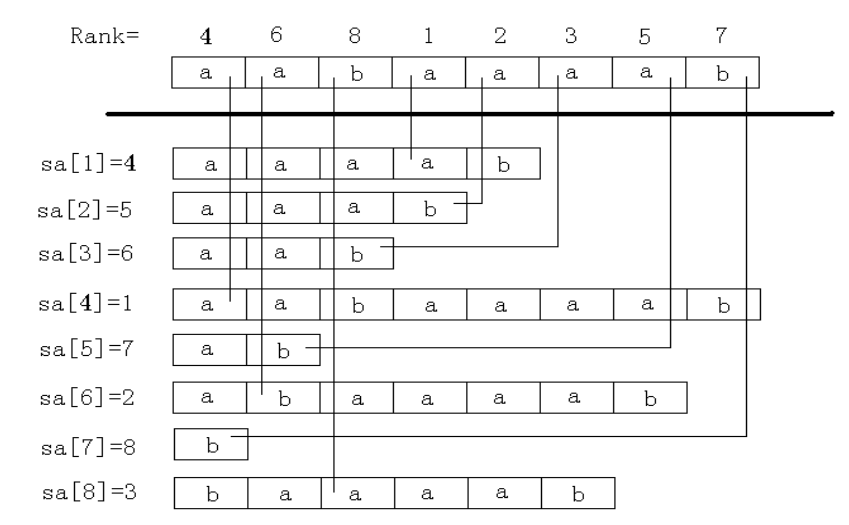
這個圖很好理解。

做法

暴力的 \(O_{n^2 \log n}\) 做法

將所有的字尾陣列都 sort 一遍，sort 複雜度為 \(O_{n \log n}\)，字串比較複雜度為 \(O_{n}\)，總的複雜度 \(O_{n^2 \log n}\)。

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

const int N = 1e6 + 5;

int n;
char s[N];
string h[N];
pair<string, int> ans[N];

int main() {
    scanf("%s", s + 1);
    n = strlen(s + 1);
    for (int i = 1; i <= n; ++ i) {
        for (int j = i; j <= n; ++ j) {
            h[i] += s[j];
        }
        ans[i] = {h[i], i};
    }
    sort(ans + 1, ans + n + 1);
    for (int i = 1; i <= n; ++ i) {
        cout << ans[i].second << ' ';
    }
    return 0;
}

倍增優化的 \(O_{n \log^2 n}\) 做法

先對長度為 \(1\) 的所有子串，即每個字元排序，得到排序後的 sa1 和 rk1 陣列。

之後倍增：

用兩個長度為 \(1\) 的子串的排名，即 rk1[i] 和 rk1[i + 1]，作為排序的第一關鍵詞和第二關鍵詞，這樣就可以對每個長度為 \(2\) 的子串進行排序，得到 sa2 和 rk2；
之後用兩個長度為 \(2\) 的子串的排名，即 rk2[i] 和 rk2[i + 2]，來作為排序的第一關鍵詞和第二關鍵詞。（為什麼是 \(i + 2\) 呢，因為 rk2[i] 和 rk2[i + 1] 重複了 \(S_{i + 1}\)）這樣就可以對每個長度為 \(4\) 的子串進行排序，得到 sa4 和 rk4；
重複上面的操作，用兩個長度為 \(\dfrac{w}{2}\) 的子串的排名，即 rk[i] 和 rk[i + (w / 2)]，來作為排序的第一關鍵詞和第二關鍵詞，直到 \(w \ge n\)，最終得到的 sa 陣列就是我們的答案陣列。

示意圖：

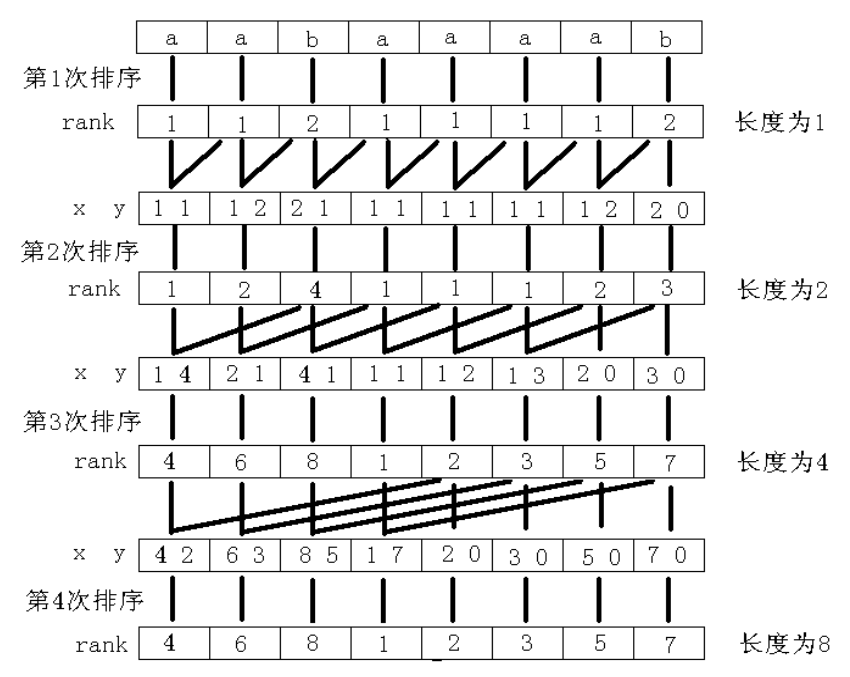
倍增的複雜度為 \(O_{\log n}\)，sort 複雜度為 \(O_{n \log n}\)，總的複雜度 \(O_{n \log ^ 2 n}\)。

排序優化的 \(O_{n \log n}\) 的做法

發現字尾陣列值域即為 \(n\)，又是多關鍵字排序，考慮基數排序。
上面已經給出一個用於比較的式子：(A[i] < A[j] or (A[i] = A[j] and B[i] < B[j]))，倍增過程中 A[i], B[i] 大小關係已知，先將 B[i] 作為第二關鍵字排序，再將 A[i] 作為第一關鍵字排序，兩次計數排序實現即可。
單次計數排序複雜度 \(O_{n+w}\)（\(w\) 為值域，顯然最大與 \(n\) 同階），總時間複雜度變為 \(O_{n \log n}\)。

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

const int N = 1e6 + 5;

int n, m;
int sa[N], oldsa[N], rk[N << 1], oldrk[N << 1], cnt[N];
// rk 第 i 個字尾的排名，sa 第 i 小的字尾的編號
char s[N];

int main() {
    scanf("%s", s + 1);
    n = strlen(s + 1);
    m = 127;

    /*--------------------------------*/

    // 計數排序

    for (int i = 1; i <= n; ++ i) {
        ++ cnt[rk[i] = s[i]];
    }
    for (int i = 1; i <= m; ++ i) {
        cnt[i] += cnt[i - 1];
    }
    for (int i = n; i >= 1; -- i) {
        sa[cnt[rk[i]] --] = i;
    }
    memcpy(oldrk + 1, rk + 1, n * sizeof(int));

    /*--------------------------------*/

    // 判重

    for (int cur = 0, i = 1; i <= n; ++ i) {
        if (oldrk[sa[i]] == oldrk[sa[i - 1]]) {
            rk[sa[i]] = cur;
        }
        else {
            rk[sa[i]] = ++ cur;
        }
    }

    /*--------------------------------*/

    for (int w = 1; w < n; w <<= 1, m = n) {

        // 先按照第二關鍵詞計數排序

        memset(cnt, 0, sizeof cnt);
        memcpy(oldsa + 1, sa + 1, n * sizeof(int));
        for (int i = 1; i <= n; ++ i) {
            ++ cnt[rk[oldsa[i] + w]];
        }
        for (int i = 1; i <= m; ++ i) {
            cnt[i] += cnt[i - 1];
        }
        for (int i = n; i >= 1; -- i) {
            sa[cnt[rk[oldsa[i] + w]] --] = oldsa[i];
        }

        /*--------------------------------*/

        // 再按照第一關鍵詞計數排序

        memset(cnt, 0, sizeof cnt);
        memcpy(oldsa + 1, sa + 1, n * sizeof(int));
        for (int i = 1; i <= n; ++ i) {
            ++ cnt[rk[oldsa[i]]];
        }
        for (int i = 1; i <= m; ++ i) {
            cnt[i] += cnt[i - 1];
        }
        for (int i = n; i >= 1; -- i) {
            sa[cnt[rk[oldsa[i]]] --] = oldsa[i];
        }

        /*--------------------------------*/

        // 更新陣列

        memcpy(oldrk + 1, rk + 1, n * sizeof(int));
        for (int cur = 0, i = 1; i <= n; ++ i) {
            if (oldrk[sa[i]] == oldrk[sa[i - 1]] && oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) {
                rk[sa[i]] = cur;
            }
            else {
                rk[sa[i]] = ++ cur;
            }
        }
    }
    for (int i = 1; i <= n; ++ i) {
        printf("%d ", sa[i]);
    }
    return 0;
}

各種常數優化

考慮我們按照第二關鍵詞排序的實質，就是將超出 \(n\) 範圍的空字串放在 sa 的最前面，在本次排序中，\(S[sa_i \dots sa_i+2^k−1]\) 是長度為 \(2^k\) 的子串 \(S[sai−2^k−1 \dots sai+2^k−1]\) 的後半截，sa[i] 的排名將作為排序的關鍵字。
\(S[sa_i,sa_i+2^k−1]\) 的排名為 \(i\)，則第一次計排後 \(S[sa_i−2^k−1 \dots sa_i+2^k−1]\) 的排名必為 \(i\)，考慮直接賦值。

for (p = 0, i = n; i > n - w; -- i) {
    oldsa[++ p] = i;
}
for (int i = 1; i <= n; ++ i) {
    if (sa[i] > w) { // 保證 sa[i] 是後半截的編號
        oldsa[++ p] = sa[i] - w; // sa[i] 一定是後半截的編號，而我們要存的是前半截的開始編號
    }
}

減小值域，每次對 rk 進行更新之後，我們都計算了一個 \(p\)，這個 \(p\) 即是 rk 的值域，將值域改成它即可。
將 rk[id[i]] 存下來，減少不連續記憶體存取。
用函數 cmp 來計算是否重複。
若排名都不相同可直接生成字尾陣列。

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

const int N = 1e6 + 5;

int n, m;
int sa[N], oldsa[N], rk[N << 1], oldrk[N << 1], cnt[N], key[N];
// rk 第 i 個字尾的排名，sa 第 i 小的字尾的編號
char s[N];

inline bool cmp(int x, int y, int w) {
    return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}

int main() {
    int i, p = 0;
    scanf("%s", s + 1);
    n = strlen(s + 1);
    m = 127;
    for (int i = 1; i <= n; ++ i) {
        ++ cnt[rk[i] = s[i]];
    }
    for (int i = 1; i <= m; ++ i) {
        cnt[i] += cnt[i - 1];
    }
    for (int i = n; i >= 1; -- i) {
        sa[cnt[rk[i]] --] = i;
    }
    for (int w = 1; ; w <<= 1, m = p) {
        for (p = 0, i = n; i > n - w; -- i) {
            oldsa[++ p] = i;
        }
        for (int i = 1; i <= n; ++ i) {
            if (sa[i] > w) { // 保證 sa[i] 是後半截的編號
                oldsa[++ p] = sa[i] - w; // sa[i] 一定是後半截的編號，而我們要存的是前半截的開始編號
            }
        }
        memset(cnt, 0, sizeof cnt);
        for (i = 1; i <= n; ++ i) {
            ++ cnt[key[i] = rk[oldsa[i]]];
        }
        for (i = 1; i <= m; ++ i) {
            cnt[i] += cnt[i - 1];
        }
        for (i = n; i >= 1; -- i) {
            sa[cnt[key[i]] --] = oldsa[i];
        }
        memcpy(oldrk + 1, rk + 1, n * sizeof(int));
        for (p = 0, i = 1; i <= n; ++ i) {
            rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++ p;
        }
        if (p == n) {
            break ;
        }
    }
    for (int i = 1; i <= n; ++ i) {
        printf("%d ", sa[i]);
    }
    return 0;
}

參考資料

字尾陣列簡介 - OI Wiki (oi-wiki.org)

「筆記」字尾陣列 - Luckyblock - 部落格園 (cnblogs.com)