一文讀懂蘋果的差分隱私技術原理

在 2016 年 6 月份的蘋果 WWDC 大會上提到了一項差分隱私技術(Differential Privacy),其作用是對使用者的資料進行擾動,然後上傳到蘋果伺服器。蘋果能通過這些擾動過的資料計算出使用者群體的行為模式,但是對每個使用者個體的資料卻無法解析。
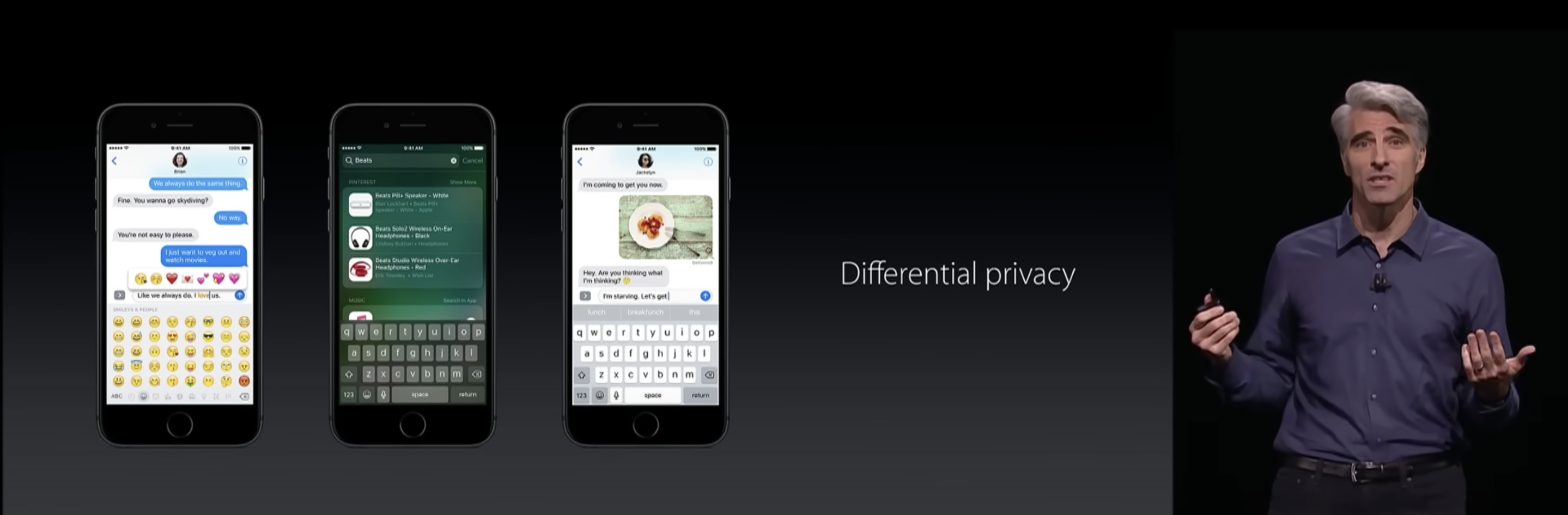
蘋果通過採用差分隱私技術,實現了在不得到使用者原始資料的前提下,學習使用者行為。如果你想知道「資料可用不可見」背後的技術,就跟著我們一起來學習下蘋果的差分隱私技術背後的原理吧!
一、簡介
差分隱私是一種資料隱私保護技術,它通過在資料中引入隨機化擾動的手段來保護隱私。簡單來說,擾動後的資料是無法精確地推斷出其原始值。同時,它允許對隨機化後資料進行統計分析,保證了資料的有用性。差分隱私提供了衡量隱私的嚴格數學定義,是近些年來業界常見的一種隱私保護技術。
1.1 差分隱私應用場景
蘋果使用在地化差分隱私(Local Differential Privacy)技術來收集使用者裝置上的資訊,其部署的產品見下表 [1, 2]。
| 產品名稱 | 用途 |
|---|---|
| QuickType suggestions | 學習熱門新詞彙,用於鍵盤打字預測 |
| Emoji suggestions(Emoji 預測) | 學習流行表情包趨勢,預測使用者使用的表情包 |
| Lookup Hints(搜尋提示) | iOS 搜尋方塊提示 |
| Safari Energy Draining Domains & Crashing Domains | 統計電量消耗大(高 CPU、高記憶體使用)的網站、易崩潰的網站 |
| Safari Autoplay Intent Detection | 統計使用者傾向於自動播放且不靜音的網站 |
| Health Type Usage | 流行的健康資料型別(睡眠、心率、卡路里等)統計 |
1.2 在地化差分隱私
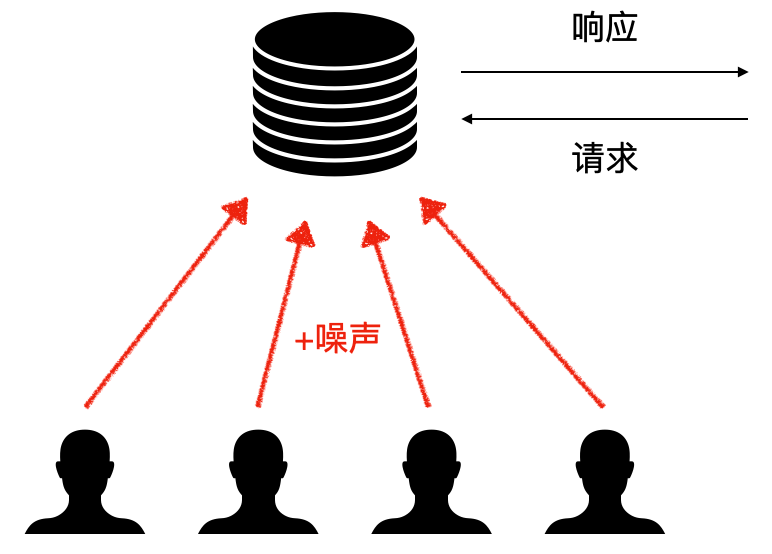
在在地化差分隱私框架中,使用者在上傳的原始資料中新增噪聲(擾動),伺服器則無法知道使用者的真實資料。這項技術最早是由 Warner 提出的隨機響應(Randomized response)[3]。
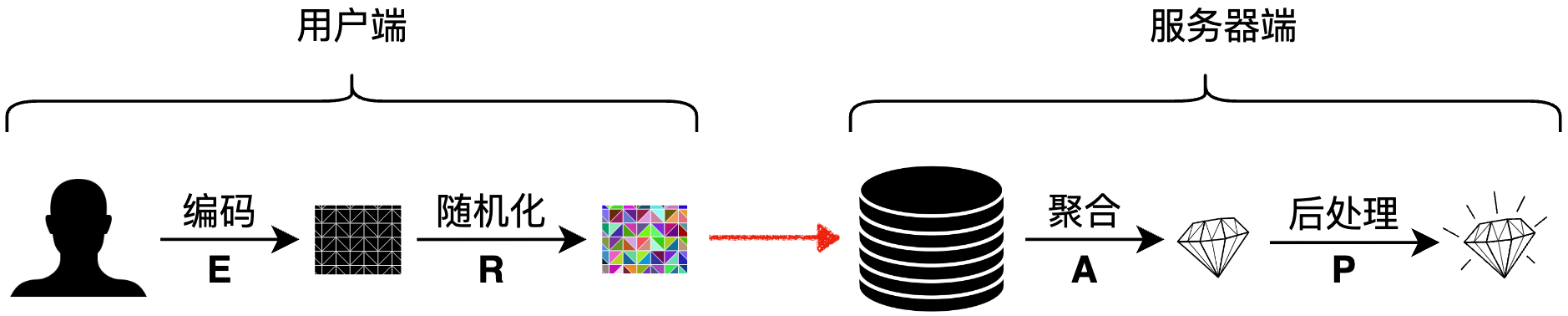
在地化差分隱私技術可用於聯合統計,比如計算平均數、中位數、頻率直方圖等。其演演算法框架(E-R-A-P)一般分為四個步驟:
- 編碼(Encoding, E)
- 隨機化(Randomizing, R)
- 聚合(Aggregation, A)
- 後處理(Post-processing, P)
使用者端進行編碼與隨機化,保證傳輸的資料是擾動後的;伺服器端進行聚合與後處理,得到相應的統計量。
二、蘋果的方案
蘋果的在地化差分隱私方案參見 [2, 4, 5],其中 [4, 5] 是專利。這裡介紹 [2] 中方案的簡易版本,以統計表情包的頻率直方圖為例。
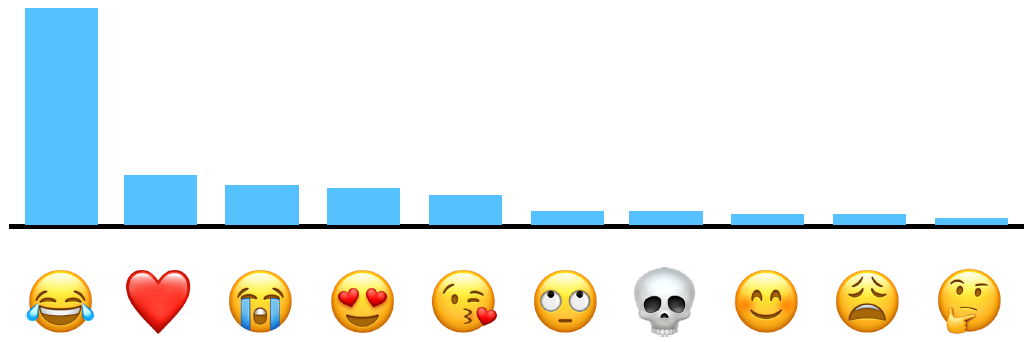
2.1 使用者端
依照上面提到的 演演算法框架(E-R-A-P),使用者端需要在上傳資料之前對做原始資料做 編碼(E) 和 隨機化(R)。
編碼(E):編碼是為了後續的隨機化和聚合步驟。蘋果的編碼採用雜湊表的方式,初始表中的元素均為「-1」。然後通過雜湊函數\(h\)將元素\(d\)(使用頻率最高的表情包)對映到位置\(h(d)\),並標記「1」。假設雜湊表的長度為\(m\)(聚合時會用到該引數)。
隨機化 (R):隨機化是差分隱私中的關鍵步驟,保證了資料的隱私性。由於編碼後的資料都是「1」和「-1」,讓每個位元以設定的概率\(p\)翻轉,即「1」變為「-1」或「-1」變為「1」。其中\(p=1/(1+e^{\epsilon/2})\),\(\epsilon\)稱為隱私預算,將在 第 2.4 節闡述。
2.2 伺服器端
依照上面提到的 演演算法框架(E-R-A-P),伺服器端需要在接收到資料後對做「擾動」後的資料做 聚合(A) 和 後處理(P)。
聚合 (A):由於每個使用者上傳的資料都是擾動後的,聚合可以消除部分噪聲的影響。假設共有\(n\)個使用者,伺服器收到使用者\(i\)的雜湊表為\(v^{(i)}\)。伺服器首先計算:
\(x^{(i)}=\frac{c_\epsilon v^{(i)}+1}{2}\),其中\(c_\epsilon=\frac{e^{\epsilon/2}+1}{e^{\epsilon/2}-1}\)
然後將所有\(x\)的對應位置累加,得到\(M\),即
則統計元素\(d\)的個數\(\tilde{f}(d)\)的公式如下,其中\(M_{h(d)}\)表示\(M\)在位置\(h(d)\)的值
可以證明\(\tilde{f}(d)\)為\(f(d)\)的無偏估計,即\(\mathbb{E}[\tilde{f}(d)]=f(d)\),其中\(f(d)\)為元素\(d\)的真實個數。這意味著估計值的期望與真實值的偏差為零,保證了估計值的無偏性。
後處理 (P):在不同應用場景中,計算的統計量可能有先驗知識,比如取值範圍的限制(如大於 0),或者保持加和不變(如統計個數),這時就需要進行後處理操作。差分隱私的性質使得任何後處理操作均不影響其結果的隱私性。
2.3 其他技術
資料隱私保護需要考慮的方面很多,僅使用差分隱私技術無法解決所有的問題。蘋果在方案中還使用了其他技術來保護資料隱私,例如資料脫敏、通訊加密、存取控制等。
- 使用者上傳的資料已移除裝置識別符號、時間戳等資訊
- 使用者與伺服器通訊使用 TLS 協定,即資料加密傳輸
- 伺服器收到使用者資料後首先移除 IP 地址、時間戳等 meta 資訊,並將資料順序打亂(shuffle)
- 資料聚合在受限存取環境中執行
- 資料只在蘋果內部流通,且蘋果的員工不能隨意存取資料
2.4 隱私預算
看到這裡大家應該明白了,差分隱私是通過在增加噪聲(擾動)來實現隱私保護,但由於擾動增加,聚合的結果會變得不精確(統計量的方差增大)。所以下面介紹平衡演演算法的隱私性和實用性的隱私預算\(\epsilon\)。
在差分隱私中隱私預算\(\epsilon\)的選取會同時影響演演算法的隱私性與實用性,稱為 Privacy-Utility 之間的權衡(trade-off)。較小的隱私預算\(\epsilon\)意味著較強的隱私保護能力。例如,資料位元隨機化擾動的概率\(p=1/(1+e^{\epsilon/2})\),減小\(\epsilon\)的取值會使得\(p\)增大,因此隱私洩漏的風險會降低,但此舉也會影響結果的精確性。

而且,雖然資料新增了差分隱私擾動,但同一使用者會不斷地上傳新資料,根據差分隱私的串型組合定理,隱私預算\(\epsilon\)會隨著時間累積逐步增加。因此,蘋果限制了使用者每天上傳資料的最大次數,並表示資料最多隻會留存三個月。
| 產品名稱 | 隱私預算\(\epsilon\)的取值 | 資料最多上傳次數 / 每天 |
|---|---|---|
| QuickType suggestions | 8 | 2 |
| Emoji suggestions(Emoji 預測) | 4 | 1 |
| Lookup Hints(搜尋提示) | 4 | 2 |
| Safari Energy Draining Domains & Crashing Domains | 4 | 2 |
| Safari Autoplay Intent Detection | 8 | 2 |
| Health Type Usage | 2 | 1 |
有研究 [6] 指出,蘋果應該解釋是如何設定隱私預算\(\epsilon\)的取值的,告知使用者並將其透明化。例如,雖然 Emoji 產品中宣稱的隱私預算\(\epsilon\)取值為 1,但通過程式碼逆向工程後發現其取值為 2(iOS 10.1.1 和 MacOS 10.12.3 版本的資料)。而且,隱私預算隨時間累積也是其方案存在的一個重要問題。
三、方案優化
第 2 節中描述的是方案的簡易版,而蘋果的方案針對通訊、統計量的精確性、場景適配等均做了優化 [2]如下:
- 為了減少雜湊碰撞的影響,實際有\(k\)個雜湊函數,每個使用者在編碼時隨機選擇一個,並將選擇的雜湊函數告訴伺服器。伺服器則構建\(k\)個雜湊表,然後進行聚合計算。
- 為了降低通訊量,蘋果的方案中對編碼後的資料進行了阿達馬變換(Hadamard transform),並通過取樣的方式,隨機選擇 1 位元的資料傳送到伺服器。這樣不僅可以降低通訊量,而且不會增加統計值的方差。
- 表情包的資料一般是固定的,但在一些場景下,使用者資料是無法預知的。比如學習熱門新詞彙,統計網站。蘋果對此採用了 Sequence Fragment Puzzle 技術,並設計了在地化差分隱私的方案。
四、無偏估計證明
這裡依舊是按照 演演算法框架(E-R-A-P)順序進行講解,證明\(\tilde{f}(d)\)是\(f(d)\)的無偏估計。
4.1 編碼
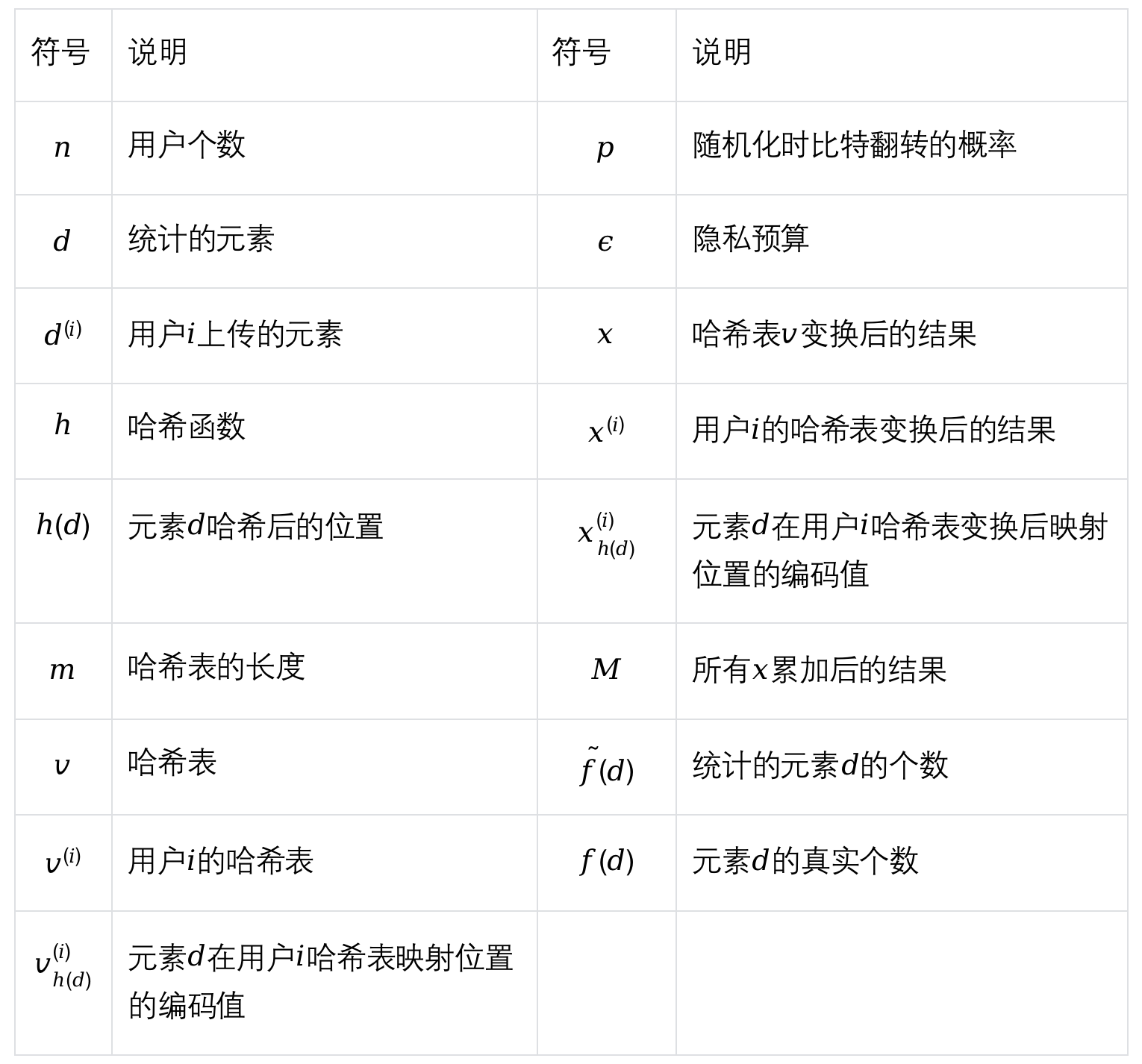
使用者\(i\)的雜湊表為\(v^{(i)}\),元素\(d\)在表中的對映位置為\(h(d)\),其對應編碼的取值為\(v^{(i)}_{h(d)}\)。使用者\(i\)上傳的元素為\(d^{(i)}\),其對應位置的編碼值為「1」,雜湊表的其餘位置為「-1」。因此當\(d^{(i)}=d\)時,\(v^{(i)}_{h(d)}\)的期望為
由於雜湊表可能會存在碰撞(衝突),即不同元素標記到了同一位置。假設資料對映到不同位置的概率是相同的,則碰撞概率為 \(1/m\)。因此當\(d^{(i)}\neq d\)時,\(v^{(i)}_{h(d)}\) 的期望為
因此\(v^{(i)}_{h(d)}\)的期望為
4.2 隨機化
隨機化時位元翻轉的概率為\(p=1/(1+e^{\epsilon/2})\)。假設隨機變數\(B\in\{-1,1\}\),\(\Pr(B=-1)=p\)。
\(\mathbb{E}[B]=p\cdot(-1)+(1-p)\cdot 1=1-2p=\frac{e^{\epsilon/2}-1}{e^{\epsilon/2}+1}=\frac{1}{c_\epsilon}\),其中\(c_\epsilon=\frac{e^{\epsilon/2}+1}{e^{\epsilon/2}-1}\)
使用者\(i\)隨機化後的雜湊表為\(Bv^{(i)}\),元素\(d\)在表中的編碼值為\(Bv^{(i)}_{h(d)}\)。
4.3 聚合
伺服器對隨機化後的雜湊表進行轉換,即計算\(x\)。元素\(d\)在使用者\(i\)雜湊錶轉換後對映位置的編碼值為\(x^{(i)}_{h(d)}\),
當\(d^{(i)}=d\)時,\(\mathbb{E}[c_\epsilon Bv^{(i)}_{h(d)}]=1\),故
當\(d^{(i)}\neq d\)時,\(\mathbb{E}[c_\epsilon Bv^{(i)}_{h(d)}]=\frac{2}{m}-1\),故
因此\(x^{(i)}_{h(d)}\)的期望為
將所有的\(x\)累加,計算\(M\),元素\(d\)在\(M\)中對映位置的編碼值為\(M_{h(d)}\),
計算其期望,其中\(f(d)\)是元素\(d\)的真實個數
由於\(\tilde{f}(d)\)是元素\(d\)個數的統計值,其計算公式為
所以
即\(\tilde{f}(d)\)是\(f(d)\)的無偏估計。
統計量的方差小才意味著估計的精確性高。關於統計量\(\tilde{f}(d)\)方差的證明請參考。
以上通過公式推導的方式證明了蘋果採用的「差分隱私」演演算法的準確性,可以實現在「資料可用不可見」的情況下實現統計計算。
五、最後
看似「高不可攀」的差分隱私技術,其實早已走進了我們的日常生活和工作中,為我們的個人隱私保駕護航。
本文通過通俗易懂的圖文和嚴謹的公式推導,講解了蘋果的差分隱私技術原理,希望能夠勾起你對隱私計算技術的興趣。最後,如果你還有什麼想了解的隱私計算相關技術,歡迎留言告訴我們!
PrimiHub 一款由密碼學專家團隊打造的開源隱私計算平臺。我們專注於分享資料安全、密碼學、聯邦學習、同態加密等隱私計算領域的技術和內容。
參考文獻
[1] Apple Differential Privacy Technical Overview. https://www.apple.com/privacy/docs/Differential_Privacy_Overview.pdf
[2] Differential Privacy Team, Apple. "Learning with privacy at scale." (2017). https://docs-assets.developer.apple.com/ml-research/papers/learning-with-privacy-at-scale.pdf
[3] Warner, Stanley L. "Randomized response: A survey technique for eliminating evasive answer bias." Journal of the American Statistical Association 60, no. 309 (1965): 63-69. https://www.jstor.org/stable/2283137
[4] Thakurta, Abhradeep Guha, Andrew H. Vyrros, Umesh S. Vaishampayan, Gaurav Kapoor, Julien Freudiger, Vivek Rangarajan Sridhar, and Doug Davidson. "Learning new words." Granted US Patents 9645998 (2017). https://patents.google.com/patent/US9645998
[5] Thakurta, Abhradeep Guha, Andrew H. Vyrros, Umesh S. Vaishampayan, Gaurav Kapoor, Julien Freudinger, Vipul Ved Prakash, Arnaud Legendre, and Steven Duplinsky. "Emoji frequency detection and deep link frequency." Granted US Patents 9705908 (2017). https://patents.google.com/patent/US9705908
[6] Tang, Jun, Aleksandra Korolova, Xiaolong Bai, Xueqiang Wang, and Xiaofeng Wang. "Privacy loss in apple's implementation of differential privacy on macos 10.12." arXiv preprint arXiv:1709.02753 (2017). https://arxiv.org/pdf/1709.02753