有了紅黑樹,為啥還要跳錶?
書接前文。
前文書《紅黑樹是怎麼來的》我們講了通過紅黑樹(本質上是 2-3 樹或者 2-3-4 樹思想)來維護二元搜尋樹的平衡性。從紅黑樹的實現來看,雖然相對於 2-3 樹來說是簡化了不少,但仍然是相當複雜的。
有沒有更加簡單的實現方案呢?
源於二分思想
在前文《二元搜尋樹的本質》中我們通過將有序陣列的二分查詢連結串列化,最終得到二元搜尋樹。
這次,我們還是從有序陣列的二分查詢開始,看看能否發明什麼新的資料結構。
和以前不同的是,這次我們先將有序陣列連結串列化:

如圖。現在我們考慮如何在該連結串列中查詢元素 40。
最簡單的做法是從表頭開始往後遍歷,時間複雜度 O(n)——顯然不是我們想要的。
我們的初步想法是:能否在這個連結串列上執行二分搜尋?
對於陣列來說,我們可以通過地址偏移立即定位到中間元素(15),然後發現 40 比 15 大,繼續對 15 後面的元素執行二分查詢即可。
連結串列的困境在於,它沒法通過地址偏移來快速定位元素。
不過我們並不死心——有沒有什麼奇技淫巧來模擬連結串列上的二分查詢?
既然對於連結串列,只能通過指標來遍歷元素,那我們能否通過給節點 1、15、60(頭尾以及二分查詢涉及到的中間元素)之間建立額外的指標來實現快速跳轉呢?
如圖:

我們建立了一個額外的連結串列(1→15→60),且該連結串列的每個節點都有一個額外指標指向下一層的同名節點。
有什麼用呢?
再來看看如何查詢元素 40。
我們可以先查上面(第二層)那個連結串列,只需兩步就走到元素 15,發現 40 介於 15 和 60(15 的下一個元素)之間,於是我們通過 15 的「下降」指標來到第一層連結串列同名節點 15,然後在第一層連結串列中繼續往後查詢。
如圖:

和直接在原始連結串列上遍歷不同,通過新增一層「索引」連結串列,我們能和二分查詢一樣「直達」中間元素,搜尋效率一下子提升了一倍。
那麼,這個查詢能否再優化一下呢?
上圖中,15 以後的搜尋仍然是線性的。我們同樣可以對 1-15、15-60 之間的兩段子連結串列再次建立「索引連結串列」:
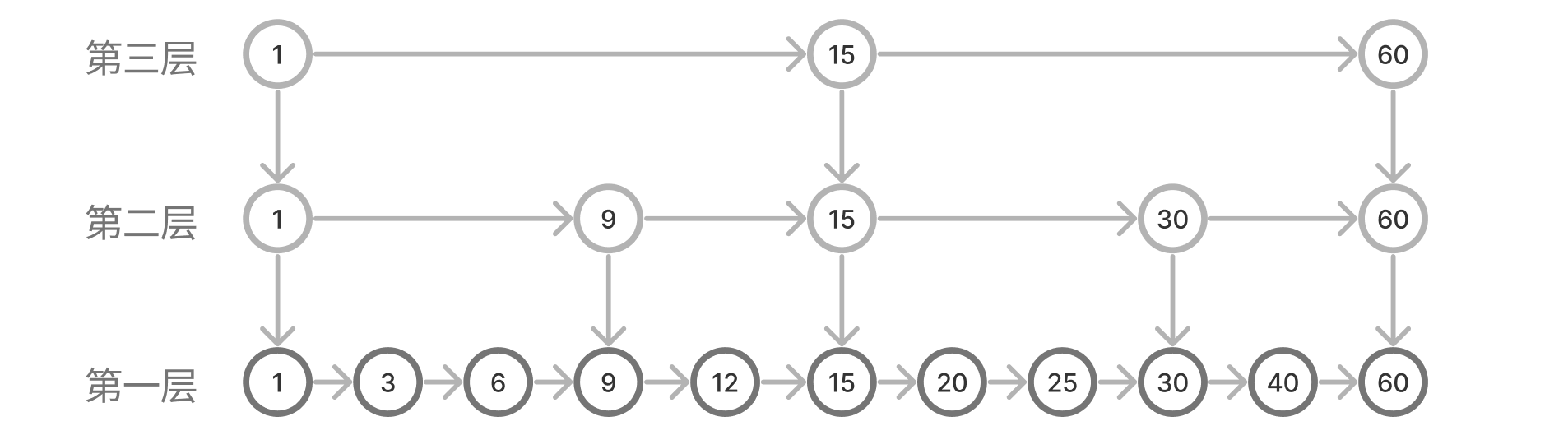
乍看有點小複雜,實際上它仍然是對二分查詢的模擬。
我們從上層往下層看。
第三層相當於執行第一次二分,標的元素是 15,然後根據實際情況到 1-15 或者 15-60 區間去查詢。
第二層則是在第三層(第一次二分查詢)的基礎上做的第二次二分,得到更細粒度的查詢區間。
所以說,如果我們從最上層索引連結串列往最下層方向逐層查詢,就相當於模擬有序陣列一次次的二分查詢。
妙哉!
我們看看建立兩層索引後元素 40 的查詢路徑:
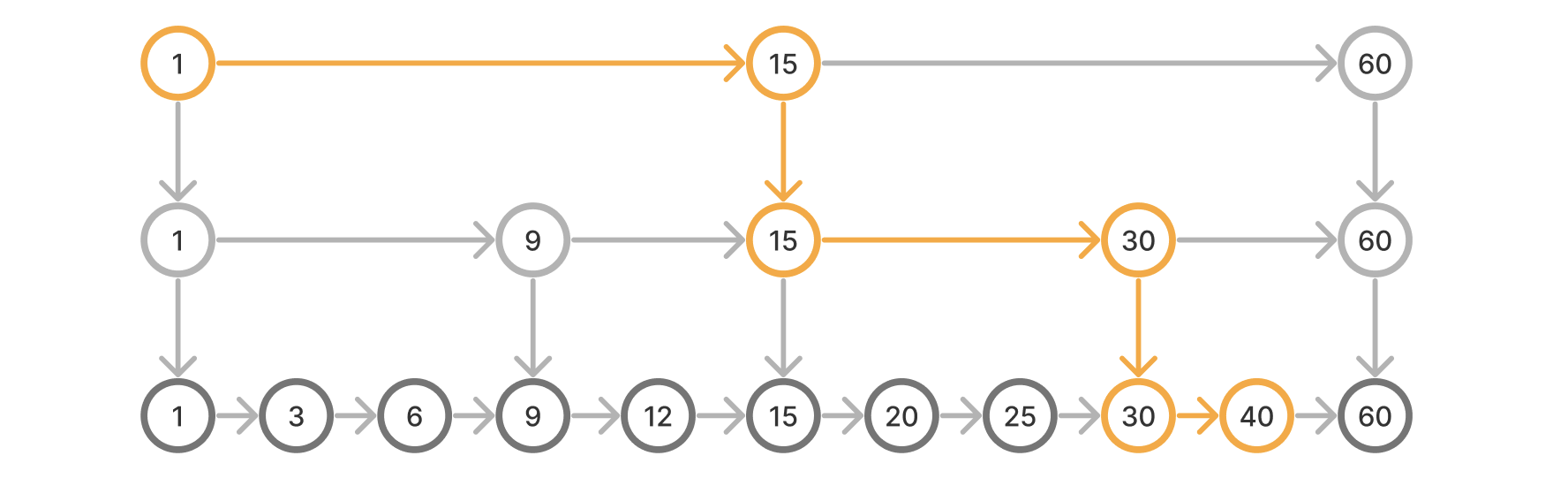
和一層相比,查詢路徑要短很多。
和普通連結串列相比,這種連結串列通過索引「跳過」了一些節點,以提升搜尋效率,因而我們給它起個「望文生義」的名字就叫跳錶(skiplist)。
由於跳錶本質上是對二分法的模擬,所以其搜尋時間複雜度同二分搜尋一樣是 O(logn)。
資料結構
跳錶的節點(最底層除外)除了要指向後繼節點(如果是雙向連結串列還要指向前驅節點),還需要指向下層同名節點,所以節點結構初步定義如下:
class Node {
key: number
val: unknown
// 後繼節點
next: Node | null
// 下層節點(比普通連結串列多出來的指標)
down: Node | null
public constructor(key: number, val: unknown) {
// ......
}
}
上圖中節點 15 表示如下:
// 第三層的 node15
const node15_l3: Node = {
key: 15,
val: 15,
next: node60_l3,
down: node15_l2,
}
// 第二層的 node15
const node15_l2: Node = {
key: 15,
val: 15,
next: node30_l2,
down: node15_l1,
}
// 第一層的 node15
const node15_l1: Node = {
key: 15,
val: 15,
next: node20_l1,
down: null,
}
我們分析一下上面的資料結構定義有沒有什麼問題。
首先說明一點,通過建立索引連結串列來提升搜尋速度屬於典型的用空間換時間。
不過,我們為同一個元素(如上例中的 15)在每一層都建立了一個獨立的物件——這是不是過於鋪張浪費了?
我們分析一下上面三個 object 的特點,看看有沒有什麼優化空間:
- 三個節點的 key、val 都是一樣的;
- 最大的不同在於 next 指標,三個節點的 next 都不一樣;
- 由圖可知,上層節點總是逐層下潛的(即第 n 層節點的 down 指標總是指向第 n - 1 層的同名節點);
所以我們可以嘗試將同一元素的各層節點合而為一:
class Node {
public key: number
public val: unknown
// 該節點各層的後繼節點指標陣列
public nexts: (Node | null)[]
public constructor(key: number, val: unknown) {
// ......
}
}
如上,我們將 next 和 down 兩個指標合入到 nexts 指標陣列中,nexts[i] 表示該節點在第 i + 1 層的後繼節點。
改造後圖示如下:

如上圖,我們做了四方面的改造:
- 各層的同名節點(同 key)合併成一個節點;
- 引入 nexts 指標陣列,node.nexts[i] 表示節點 node 在第 i + 1 層的後繼節點;
- 為編碼上的方便,引入哨兵節點 head(不表示任何實際節點);
- 不再對尾節點(圖中的 60)建立索引(沒有必要,程式設計中用 null 值判斷即可);
最後我們定義出完整的資料結構:
class SkipList {
// 表頭指標。為方便處理,表頭不表示實際節點, 作為哨兵存在
protected head: Node
// 跳錶中元素個數
protected length: number
// 跳錶層數
protected level: number
public constructor() {
// 建立表頭
this.head = new Node(-Infinity, undefined)
this.length = 0
this.level = 0
}
}
查詢元素
我們看看如何查詢節點 40。
任何查詢都從表頭 head 且從最上層開始,到第一層為止:
- 取 head.nexts[2],是 15,小於 40,則取 node15 繼續比較;
- 取 node15.nexts[2],是 null,說明不能再往後找了,則下降到第二層(nexts 下標 1);
- 取 node15.nexts[1],是 30,小於 40,則取 node30 繼續比較;
- 取 node30.nexts[1],是 null,說明不能再往後找了,則下降到第一層(nexts 下標 0);
- 取 node30.nexts[0],是 40,找到,返回並結束;
如圖:

程式碼如下:
class SkipList {
// ......
/**
* 根據 key 查詢 value 並返回,如果沒找到則返回 undefined
* @param key
*/
public search(key: number): unknown {
if (!this.length) {
return
}
// 從 head 開始找
let node = this.head
// 從最高層開始往下搜尋,直到搜到第一層
for (let i = this.level - 1; i >= 0; i--) {
// 如果當前節點該層存在後繼節點,且該後繼節點的 key 小於等於目標 key,則跳到該後繼節點
while (node.nexts[i] && node.nexts[i].key <= key) {
node = node.nexts[i]
}
// 從 node 進入到下一層繼續查詢
}
return node.key === key ? node.val : undefined
}
}
超簡單有沒有!
索引層數
在講插入之前,我們先思考一個問題:連結串列中的某個元素應該有多少層(或者說需要給它建多少層索引)?
前面我們通過二分法推匯出多層索引的概念。但如果在實際操作中,每次插入一個元素後都用二分法思想去確定元素的索引層數,可能一次插入會導致大範圍的索引重建(比如原本通過二分法拿到標的節點是 a,插入新元素後再次二分拿到的標的很可能不再是 a)。
我們也可以採用類似 B 樹的裂變思想,比如我們規定第 n 層兩個節點之間所囊括的 n - 1 層元素數量不可超過 x,一旦超過就觸發裂變以生成新的索引(裂變可能是級聯的)。不過其實現起來也比較複雜。
跳錶的設計採用了一種簡單粗暴但很有效的方法:概率法。
思想是這樣的:我們規定第 n 層的元素數量是其下一層(n - 1)數量的 1/N。換句話說,一個元素有 1/N 的概率會向上建一層索引。
以 N = 4 為例。
假設我們想插入元素 22——該元素需要建立幾層索引呢?
有 3/4 的概率不建立任何索引(也就是隻有最底下一層)。
有 1/4 的概率建立 1 層索引。
有 1/4 * 1/4 即 1/16 的概率建 2 層索引。
有 1/4 * 1/4 * 1/4 即 1/64 的概率建 3 層索引。
依此類推。
如此得到的資料結構本質上是一棵 N 叉樹(這裡是 4 叉樹)。
我們通過如下程式碼計算一個新節點的層數資訊:
class SkipList {
// 最大層數限制
protected static readonly MAX_LEVEL = 32
// 上層元素數是下層數量的 1/N(相當於 N 叉樹)
protected static readonly N = 4
// ......
/**
* 隨機生成 level 層數
* 從最底層開始,每增加一層的概率為 1/N
*/
protected randomLevel(): number {
let level = 1
while (Math.round(Math.random()*10000000) % SkipList.N === 0) {
level++
}
return Math.min(level, SkipList.MAX_LEVEL)
}
}
這裡我們通過將生成的亂數對 N 取模和 0 比較來模擬 1/N 的概率(比如 N = 4,則取模後為 0-3)。
插入元素
我們看如何插入元素 22。
首先要確定 22 在原始連結串列(第一層連結串列)中的位置,該過程實際就是搜尋過程,時間複雜度 O(logn)。
搜尋過程如圖:

我們找到應該在 20 和 25 兩個節點之間插入 22。
假如我們通過 randomLevel() 得到層數是 5,插入後整個跳錶長這樣:

觀察上圖發現:
- 每層都有 next 指標指向該新節點,具體來說就是搜尋路徑上各層最右搜尋節點(15、15、20)的 next 指標指向新節點;
- 新層(最高兩層)的前驅節點都是 head;
- 新節點的各層 next 指標指向該層前驅節點的 next 原值;
經上面分析發現,整個插入過程中,關鍵是找出每層的前驅節點。程式碼如下:
class SkipList {
/**
* 搜尋鍵碼 key,返回其搜尋路徑上經過的每層的前驅節點陣列
* 即每層返回其左邊相鄰節點
* @param key - 關鍵字
* @returns 關鍵字 key 在每層的前驅節點陣列
*/
private searchPrevNodes(key: number): Node[] {
// 記錄每層走到的最右邊的位置(也就是目標節點的前驅節點)
const prevNodes: Node[] = []
// 從 head 開始
let node = this.head
// 從最上層開始往下找
for (let i = this.level - 1; i >= 0; i--) {
// 如果當前節點該層存在後繼節點,且該後繼節點的 key 小於 key,則跳到該後繼節點
while (node.nexts[i] && node.nexts[i].key < key) {
node = node.nexts[i]
}
// 下沉之前記錄該節點作為本層存取到的最右節點
prevNodes[i] = node
}
// 如果一個都沒有(列表為空,this.level = 0 時),將 head 加入進去
if (!prevNodes.length) {
prevNodes[0] = this.head
}
return prevNodes
}
}
元素插入邏輯程式碼如下:
class SkipList {
// ......
/**
* 將 { key, val } 插入到跳錶中
*/
public insert(key: number, val: unknown) {
// 獲取搜尋路徑上的各層前驅節點
const prevNodes = this.searchPrevNodes(key)
// 建立新節點
const newNode: Node = { key, val, prev: null, nexts: [] }
// 計算新節點的索引層數
const level = this.randomLevel()
// 逐層處理 next 指標
for (let i = 0; i < level; i++) {
// prevNodes 裡面僅有原先 this.level 層的最右 node,而新 level 可能高於原 level,
// 該情況下,超出的層在 prevNodes 裡面沒有對應節點,則直接取 head
const leftNode = prevNodes[i] ?? this.head
// 變更 next 指標
newNode.nexts[i] = leftNode.nexts[i]
leftNode.nexts[i] = newNode
}
if (level > this.level) {
this.level = level
}
this.length++
}
}
插入過程的平均時間複雜度是 O(logn)。
刪除元素
考慮刪除節點 22,刪除後整個跳錶結構如下:

跳錶元素的刪除本質就是插入的逆操作:將該節點從各層抹除,即將該節點各層的前驅節點的 next 指標指向該節點在該層的後繼節點。
插入過程中可能產生新的層(head 層數隨之增長),而刪除則可能造成層數減少(head 層數收縮)。
通過觀察圖示不難發現,刪除後和插入前的結構竟然是一模一樣的,如此的穩定性真讓人嘆為驚奇。
不同於其他平衡樹,跳錶的插入和刪除不但完全互逆,而且也沒有複雜的遞迴重建過程——這正是跳錶這種概率型資料結構的簡單性之精華所在。
刪除程式碼如下:
class SkipList {
// ......
public delete(key: number) {
// 獲取搜尋路徑上的各層前驅節點
const prevNodes = this.searchPrevNodes(key)
// 待刪除的節點就是第一層前驅節點的該層 next 指標所指向的節點
const current = prevNodes[0].nexts[0]
if (!current || current.key !== key) {
return
}
// 從下往上,處理各層的 next 指標
// 需要處理的層:待刪節點的索引層數
for (let i = 0; i < current.nexts.length; i++) {
prevNodes[i].nexts[i] = current.nexts[i]
current.nexts[i] = null
// 如果該層的前驅節點是 head,且調整後其 next 指向 null/undefined,說明該層不再有有效節點,需要將層數減 1
if (!this.head.nexts[i]) {
this.level--
}
}
this.length--
}
}
簡單性的源頭
對比紅黑樹的插入和刪除實現,你會驚於跳錶的實現是如此簡單。為何?
我們假設不使用概率來決定新節點的索引層數,就很可能需要採用類似 B 樹的方案,通過限制兩索引節點之間所轄節點數來決定索引的分裂與合併。比如規定任何兩索引節點之間所轄節點數必須在 N/2 到 N 之間,小於 N/2 則謀求合併,超過 N 則分裂。如此必然會帶來複雜的級聯分裂與合併邏輯。
相反,跳錶採用了簡單粗暴但同樣有效的概率法,在插入元素的時候,通過概率計算得出索引層數,而更新索引(插入和刪除)僅影響該節點在各層的前驅節點,影響非常小,更新過程異常簡單。
所以說,這種資料結構的概率性帶來了其簡單性。
總結
- 我們通過有序陣列的二分查詢思想推匯出鏈式資料結構的二分法:多級索引;
- 通過概率決定每個元素的索引層數,在理論正確性的前提下保證了實現的簡單性;
- 插入和刪除操作的關鍵是找出目標節點在每層的前驅節點;
- 插入和刪除操作是完全互逆的,表明跳錶具備很好的動態穩定性;
- 跳錶和紅黑樹的各項操作具備同級別的時間複雜度,但比紅黑樹實現起來更加簡單,範圍查詢也更加直觀高效(直接定位到起始節點,然後直接在第一層順序遍歷即可),所以現在很多專案都採用了跳錶這種資料結構(如 Redis、Lucene、LevelDB 等);
另外,分級索引是人類資訊檢索領域的一個重要思想,圖書檢索、書本目錄、檔案系統、域名(DNS 查詢)、ip 地址、作業系統頁表等等的設計都體現了該思想。
本文完整程式碼參見 github: https://github.com/linzier/algo-ts。
為講解的簡單性,本文使用的是單向連結串列,github 中實現的是雙向連結串列。