引子

有時候我們需要計算一個函數的定積分，粗略上可以使用估算的方法。如圖所示，將原本的曲線粗略地看成一個梯形。這個方法叫梯形法則（Trapezoidal Rule）。也叫做一階牛頓-柯特斯閉型積分公式。

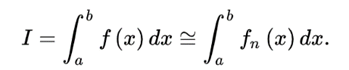
其中

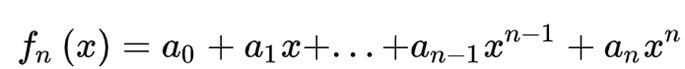
所謂一階，指的就是n=1的情況。

最理想的情況就是把這個影象分割成無數個梯形，便可求出對應的定積分。

但是在實際操作的情況下，梯形法則為了保證速度無法取極多的點，這樣照成梯形法則誤差較大。

分割成無限個梯形其實就等效於

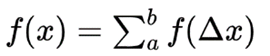
因此我們將考慮更高階的公式，本文將要介紹的便是二階牛頓-柯特斯閉型積分公式（辛普森法）。 即將函數近似看成一條拋物線。顯然一階牛頓-柯特斯閉型積分公式需要在首尾取兩個點方可得到f(x)的解析式。而二階要得到一個拋物線方程則需要取三個點，才能得到解析式。而牛頓-柯特斯閉型積分公式都採用等距取點的方法，所以辛普森法需要取首尾點以及中間點。

推導方法

通過辛普森法，只需要計算出邊界和中點的函數值就可以得到估算的函數的積分

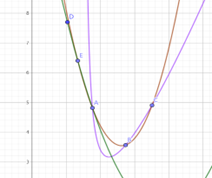
綠色是被積函數，紅線是使用梯形法則得到的，藍線是辛普森法得到的。可以發現相對梯形法則，辛普森法相對而言更符合被積函數。繼續提高n的值可以提高估算的準確度，但顯然也會提高計算的複雜性，而二階的對於圖中的函數基本上可以達到要求。

　　對於一段基本符合二次函數的函數，辛普森法可以得到較為準確的結果，然而當函數變得複雜時。辛普森將出現明顯的誤差。這時候該怎麼計算積分。

擺在面前的有兩條路，一個是不斷細分割區間，再將區間求和，另一條是增加n的值，使得函數更加符合被積函數。本文主要討論第一種方法。

正文

走第一條路，如果採用將區間平均細分為若干份，求得各個區間的積分後再統一求和，這樣在計算量上和梯形法則上相等，但是精度提升不了多少。

　　然而，不得不承認，對於一個函數而言，存在二次擬合比較好的地方，也存在比較差的地方。如果在擬合比較好的地方細分就會浪費計算資源，而統一的平均細分，也導致在擬合比較差的地方達不到想要的精度。

因此，如何在擬合好的地方降低細分程度，擬合差的地方提高細分進度成了重中之重。

而本文想介紹的關鍵自適應辛普森積分法，就是解決這個問題的。

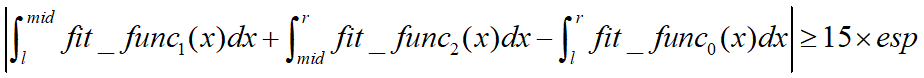
上式是自適應辛普森積分法是否對一個區間進行細分的判定條件。

其實是根據這個結論：

來源

原理其實很簡單，首先將這個區間進行二分為兩個區間肯定能得到更為精準的結果，如果這個結果和直接計算該區間的辛普森積分得到的結果差距大於某一個值，則認為對這個區間繼續細分是有意義的，反之差距小於該值則說明繼續細分對提高精度沒有什麼幫助，就不進行下一步的細分，以降低計算的複雜度。這個值一般是esp的15倍（至於為什麼是15倍可以看看這篇文章Notes on the Adaptive Simpson Quadrature Routine），調節esp可以控制估計值和精確值在多少位前是一樣的。

擴充套件：為什麼二分一個區間能夠得到一個更精確的結果，從影象上很好理解，兩個函數要比一個函數擬合得更緊密。從數值上說明是因為辛普森演演算法的誤差公式為

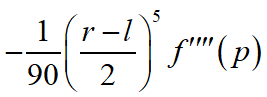
p是f(x)在[l,r]區間內使得f(x)四階導數取得最大值的值。具體證明可以參考A short proof of the error term in Simpson's rule（看不懂？本筆者也看不懂）。根據琴生不等式可以推匯出區間一分為二後的誤差和小於不一分為二的誤差（大概可以證明吧，以後有時間證明一下QAQ）。

據說（美）薩奧爾（Sauer, T.）著；裴玉茹，馬賡宇譯.數值分析（原書第2版），機械工業出版社，第240頁。有相對完善的介紹，以後買一本看看。

程式碼

#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;

double F(double x)
{
    return x * log(x);
}
double PF(double x)
{
    return 1.0 / 2.0 * x * x * log(x) - 1.0 / 4.0 * x * x;
}
//primitive function: 1/2xlnx-1/4x

int count_simpson =0;

double simpson(double l,double r)
{
    count_simpson++;
    return (r - l) / 6.0 * (F(l) + F(r) + 4 * F((r + l) / 2));
}

double asr(
    double l,//區間左邊界
    double r,//區間右邊界
    double integral,//該區間的辛普森積分
    double esp
)
{
    double mid = (l + r) / 2;
    double in_l = simpson(l, mid), in_r = simpson(mid, r);
    if (fabs(in_l + in_r - integral) > esp * 15) //細分有價值
        return asr(l, mid, in_l, esp) + asr(mid, r, in_r, esp);
    else
        return in_l + in_r + (in_l + in_r - integral) / 15.0;//返回這個肯定比返回integral精度更高
}


int main()
{
    cout << setprecision(16)<<"估算" << asr(1, 8, simpson(1, 8), 1e-7) << "  &&  精確" << PF(8) - PF(1) << endl;
    cout << "計算次數:" << count_simpson << endl;
    return 0;
}

執行結果：

擴充套件

為什麼我非要用辛普森，這個演演算法為什麼不能用梯形法則代替辛普森的作用？其實是可以用梯形法則代替辛普森的。

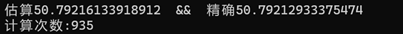
但是無論是計算量還是精度來說效果都不是很好（QAQ）。不用更高階的原因也很簡單，提高階增加編碼難度同時提高的精度難以彌補耗時。

後記

高考和強基計劃稽核結束，筆者如願以償地被理想的大學錄取，由於錄取專業與數學強相關，日後更新的檔案也將高度圍繞數學方面展開。這個排版調了我半天，emm，以後還是老老實實用markdown吧。

自適應辛普森法積分演演算法推導

引子

正文

程式碼

擴充套件

後記