我堅定的認為,這個原始碼肯定是有 BUG 的!
你好呀,我是歪歪。
上週我不是發了《我試圖給你分享一種自適應的負載均衡。》這篇文章嘛,裡面一種叫做「自適應負載均衡」的負載均衡策略,核心思路就是從多個服務提供者中隨機選擇兩個出來,然後繼續選擇兩者中「負載」最小的那個節點。
前幾天有讀者看了文章後找到我,提出了兩個問題。
有點意思,我給你盤一下。
第一個問題
第一個問題是這樣的:
他的圖片,指的是文章中的這個部分:
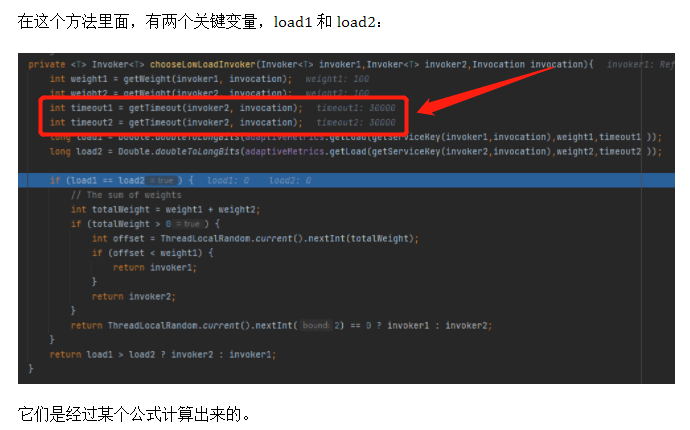
當時我也沒有細看,所以我的回覆是 timeout 是個設定項,我這裡取出來都是 30000 的原因是因為我沒有進行設定。
然後,他對於問題進行了進一步的描述:
1scfi0uweo0.png)
我點到原始碼裡面一看,好傢伙,它是這樣寫的:
int timeout1 = getTimeout(invoker2, invocation);
int timeout2 = getTimeout(invoker2, invocation);
兩次呼叫 getTimeout 方法的入參一模一樣。這個地方你用腳指頭想也應該能知道它的引數傳遞錯誤了嘛。
我甚至能猜到作者寫這一行程式碼的時候,按了一個 ctrl+d 快捷鍵,複製了一行出來,結果只是把前面的 timeout1 改成了 timeout2,忘記改後面了。
這種低階錯誤...
我也犯過好幾次。

然後我叫這個讀者可以去提一個 pr,以後出去吹牛的時候就可以說:我曾經給 apache 頂級開源專案貢獻過原始碼。
但是這個讀者可能比較低調,把這個機會讓給我了。
於是...
我就厚著臉皮去提 pr 了,然後被 merge 了:
https://github.com/apache/dubbo/pull/12636
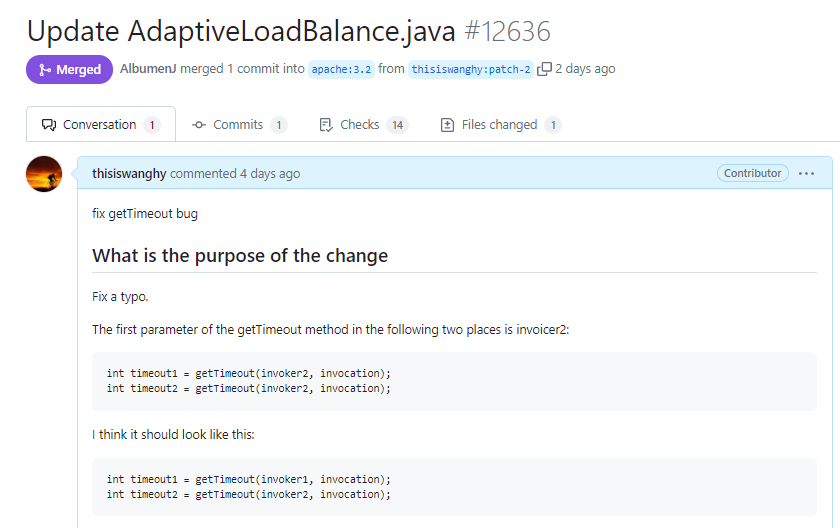
把 invoker2 修改為 invoker1,搞定。
舒服了,在我四處混 pr 的光榮事蹟中,又新增了濃墨重彩的一筆。

第二個問題
第二個問題,其實我在之前的文中也提到了。
文章裡面對於「隨機選擇兩個」出來這個動作的程式碼實現,我感覺是有 BUG 的,所以提出了一個大膽的質疑:
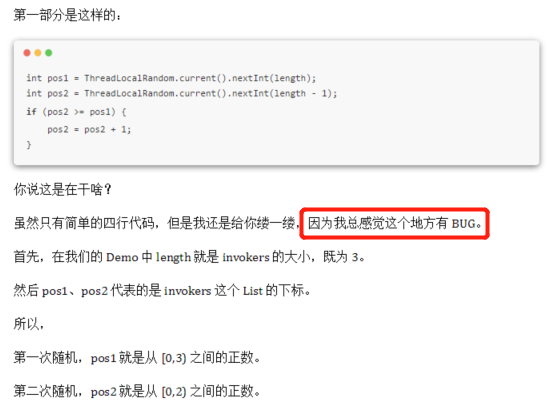
但是秉著「又不是不能用」的核心思路,當時也沒有細想。
當我前面的那個 pr 被 merge 的時候,我決定:要不好人做到底,把這個 BUG 也幫它們修復一下吧。
首先,我來詳細解釋一下,我為什麼會認為這個地方有 BUG。
首先,把它的整個原始碼拿過來:
int pos1 = ThreadLocalRandom.current().nextInt(length);
int pos2 = ThreadLocalRandom.current().nextInt(length - 1);
if (pos2 == pos1) {
pos2 = pos2 + 1;
}
我就以最簡單的情況,只有三個服務提供者,即 length=3,然後隨機選兩個出來,這種情況來進行說明。
我也不進行數學論證了,直接就是給你表演一個窮舉大法。
首先,我們的 invokers 集合裡面有三個服務提供方,invoker1,invoker2,invoker3:
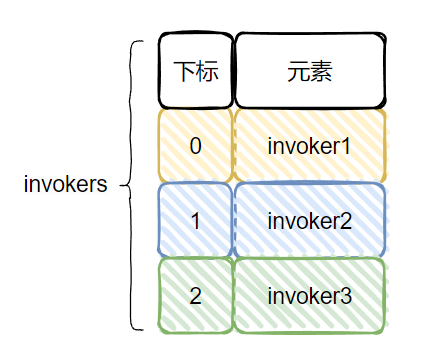
當執行這一行程式碼的時候:
int pos1 = ThreadLocalRandom.current().nextInt(length);
length=3,即
int pos1 = ThreadLocalRandom.current().nextInt(3);
所以 pos1 的取值範圍是 [0,3)。
前面說了,我要用窮舉大法,所以我們要分析 pos1 分別為 0,1,2 的時候。
pos1=0
首先,我們分析 pos1=0 的情況。
當 pos1=0 時,我們要算 pos2 的值,當執行這行程式碼的時候:
int pos2 = ThreadLocalRandom.current().nextInt(length - 1);
它的取值範圍是 [0,2)。
所以,經過兩行隨機的程式碼之後,我們能得到這樣的組合:
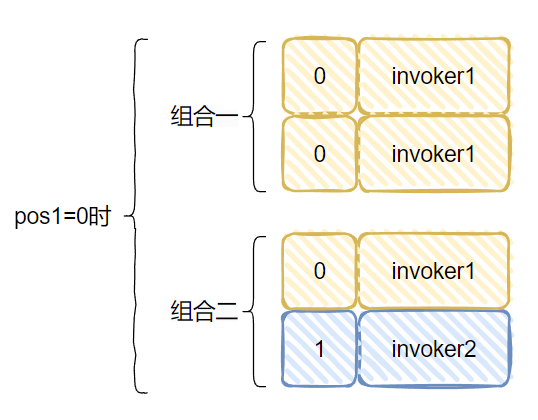
針對組合一,又因為有這個判斷在這裡:
if (pos2 == pos1) {
pos2 = pos2 + 1;
}
當 pos2 = pos1,即隨機到同一個下標的時候,pos2 需要加一,以免使用同一個 invoker。
所以,當 pos1=0 時,隨機的最終只會是這兩種情況:
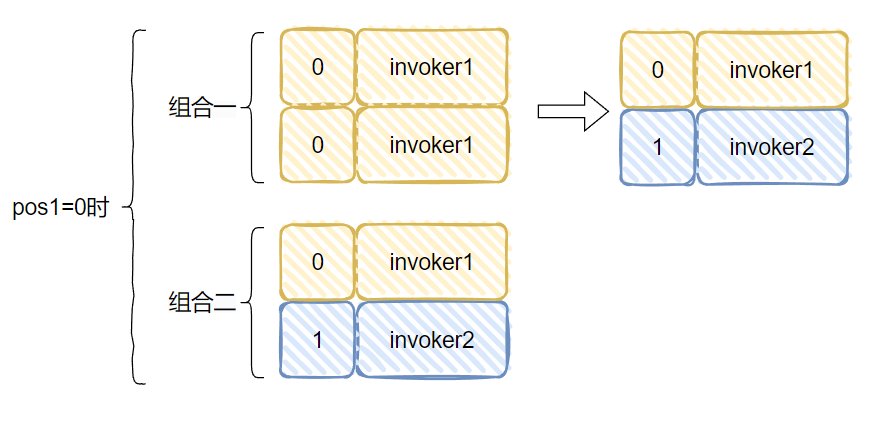
pos1=1
同理,我們可以得出 pos1=1 時,情況是這樣的:
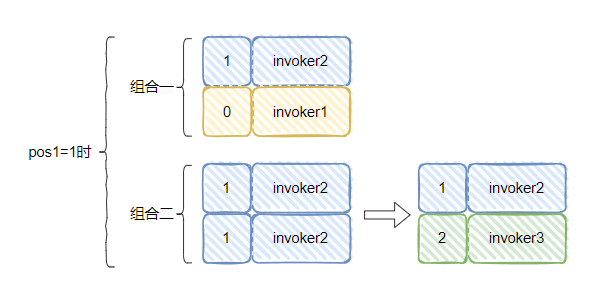
pos1=2
當 pos1=2 時,情況是這樣的:
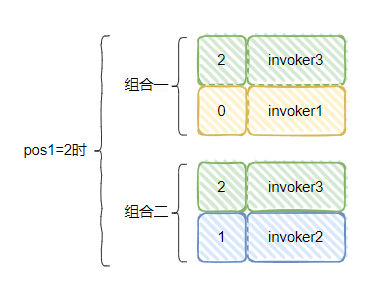
彙總
此時,我們所有情況都分析完成了,窮舉大法已經使用完畢。
這個時候我們把所有的情況組合起來看一下:
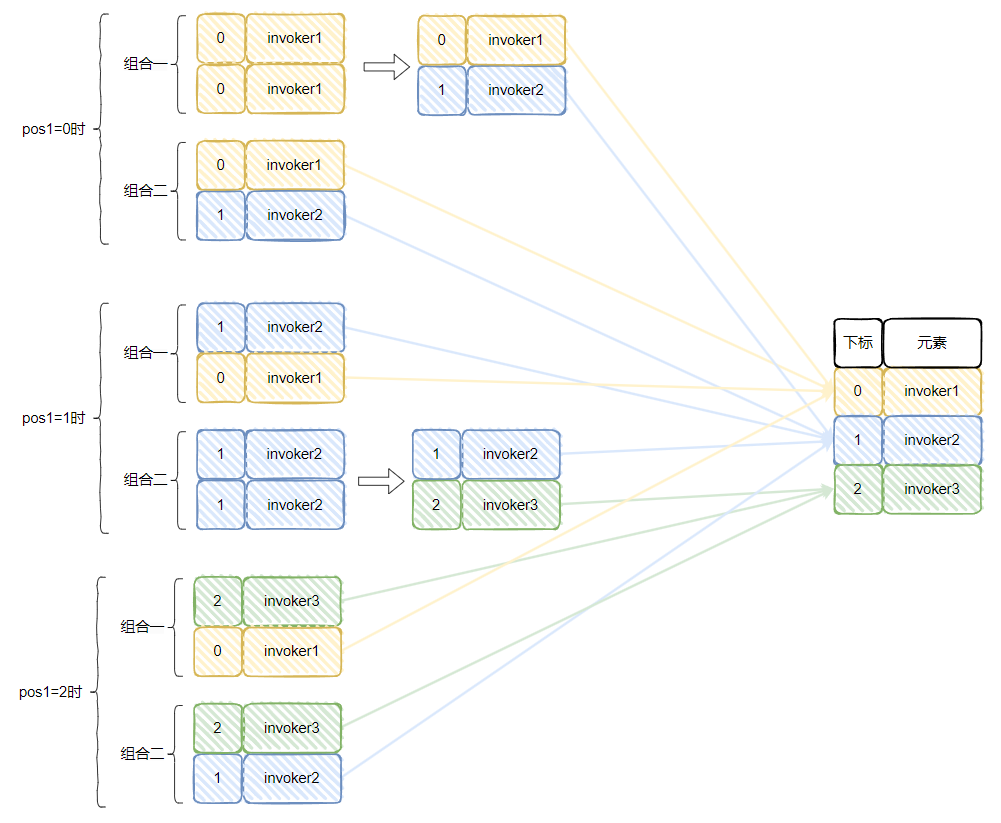
invoker1 被選中了 4 次 invoker2 被選中了 5 次 invoker3 被選中了 3 次
來,請你大聲點的告訴我,這個演演算法是不是公平的?

都不是 1:1:1 了,還公平個啥啊。
所以,我在之前的文章裡面是這樣說的:

事實也證明了,確實是對於最後一個元素是不公平的。
於是,我開始準備著手敲程式碼,打算再混一個 pr。
我想換成的原始碼也很簡單。因為它核心目標是從 list 集合中隨機返回兩個物件嘛。
那我直接就是這樣:
Object invoker1 = invokerList.remove(ThreadLocalRandom.current().nextInt(invokerList.size()));
Object invoker2 = invokerList.remove(ThreadLocalRandom.current().nextInt(invokerList.size()));
你仔細的嗦一嗦這個程式碼,是不是很公平?
當一個元素被選中之後,我就把它給踢出去。這樣第二次隨機的時候,invokerList.size() 的值就實現了減一的邏輯。
既可以保證第二次隨機的時候,不會隨機到一樣的元素。
也可以保證剩下的每個元素都有機會再次參與到隨機過程中。

為此,我還專門寫了一個 Demo 來驗證這個寫法:
public class MainTest {
private final static HashMap<Integer, Integer> COUNT_MAP = new HashMap<>();
public static void main(String[] args) {
for (int i = 0; i < 100000; i++) {
List<Integer> list = new ArrayList<Integer>();
list.add(1);
list.add(2);
list.add(3);
Integer invoker1 = list.remove(ThreadLocalRandom.current().nextInt(list.size()));
Integer invoker2 = list.remove(ThreadLocalRandom.current().nextInt(list.size()));
posCount(invoker1);
posCount(invoker2);
}
System.out.println(COUNT_MAP);
}
public static void posCount(Integer key) {
Integer pos1Integer = COUNT_MAP.get(key);
if (pos1Integer == null) {
COUNT_MAP.put(key, 1);
} else {
pos1Integer++;
COUNT_MAP.put(key, pos1Integer);
}
}
}
你粘過去就能跑,執行 10w 次,每個元素被選中的總次數基本上就是 1:1:1。
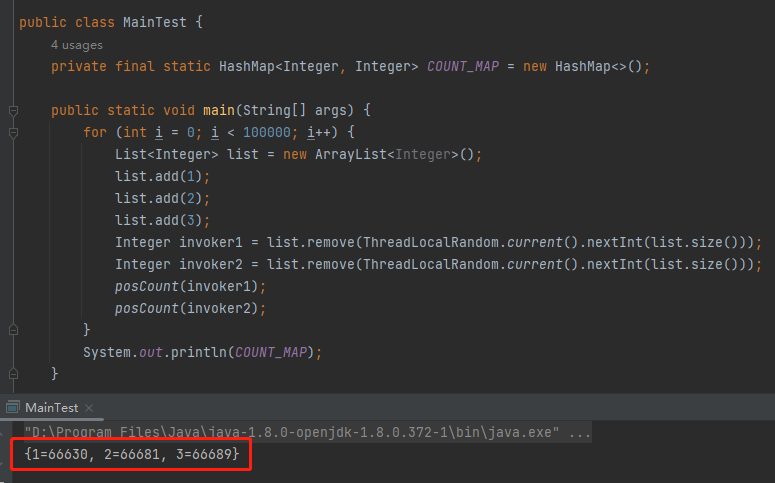
而把 Dubbo 原始碼裡面的實現拿過來:
public class MainTest {
private final static HashMap<Integer, Integer> COUNT_MAP = new HashMap<>();
public static void main(String[] args) {
List<Integer> list = new ArrayList<Integer>();
list.add(1);
list.add(2);
list.add(3);
int length = list.size();
for (int i = 0; i < 100000; i++) {
int pos1 = ThreadLocalRandom.current().nextInt(length);
int pos2 = ThreadLocalRandom.current().nextInt(length - 1);
if (pos2 >= pos1) {
pos2 = pos2 + 1;
}
posCount(pos1);
posCount(pos2);
}
System.out.println(COUNT_MAP);
}
public static void posCount(Integer key) {
Integer pos1Integer = COUNT_MAP.get(key);
if (pos1Integer == null) {
COUNT_MAP.put(key, 1);
} else {
pos1Integer++;
COUNT_MAP.put(key, pos1Integer);
}
}
}
也跑 10w 次,執行結果是這樣的:
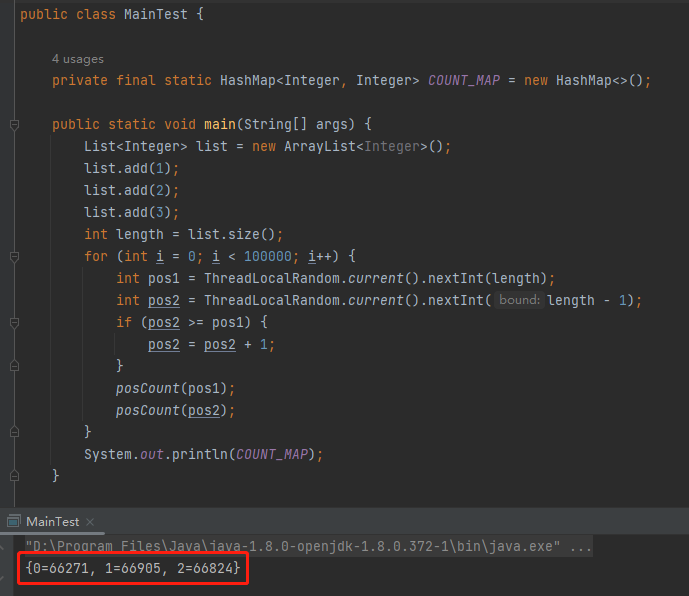
...
...
...
臥槽,等等,怎麼回事,居然也是接近 1:1:1 的?
我當時看到這個執行結果的時候,表情大概是這樣的:

這玩意,和我分析出來的不一樣啊。
反轉
其實也不能算是反轉吧。
因為我前面分析的時候,給的程式碼是這樣的:
if (pos2 == pos1) {
pos2 = pos2 + 1;
}
而真實的原始碼是這樣的:
if (pos2 >= pos1) {
pos2 = pos2 + 1;
}
一個是 ==,一個 >=。
當我把這裡換成 == 的時候,執行結果就不再是 1:1:1 了,符合我前面窮舉大法分析的情況。
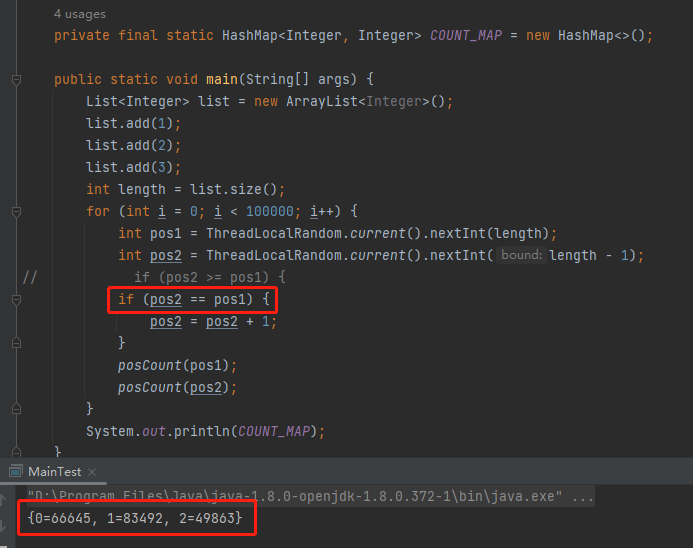
而在我的潛意識裡面,第一次看程式碼的時候,我一直以為這個部分的程式碼就是 ==,所以我一直按照 == 進行的分析,從而覺得它有問題。
這波,我覺得得讓潛意識來背鍋。

當是 >= 的時候,我們只需要重新分析一下 pos1=0 的情況。
組合一,0>=0,滿足條件,最終 pos1=0,pos2 會加一,變成 1,所以還是會變成之前分析的情況:
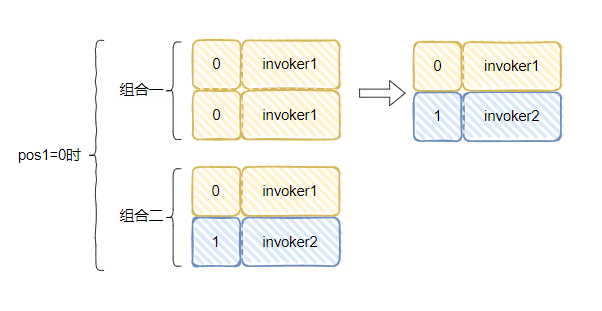
當時對於組合二,情況就發生了微妙的變化。
組合二,1>=0,滿足條件,最終 pos1=0,pos2 會加一,變成 2,所以就變成了這樣:
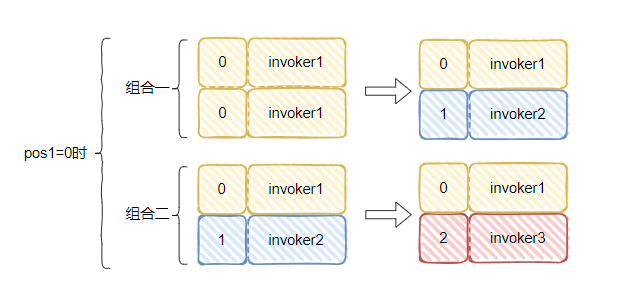
invker2 被替換為了 invoker3。
還記得我們之前,按照 == 的情況,分析出來的比例嗎?
invoker1 被選中了 4 次 invoker2 被選中了 5 次 invoker3 被選中了 3 次
此時,我們按照 >= 的情況分析,invoker2 被替換為了 invoker3。
那麼比例就變成了:
invoker1 被選中了 4 次 invoker2 被選中了 4 次 invoker3 被選中了 4 次
所以,回到我最最開始說的讀者提出的第二個問題:
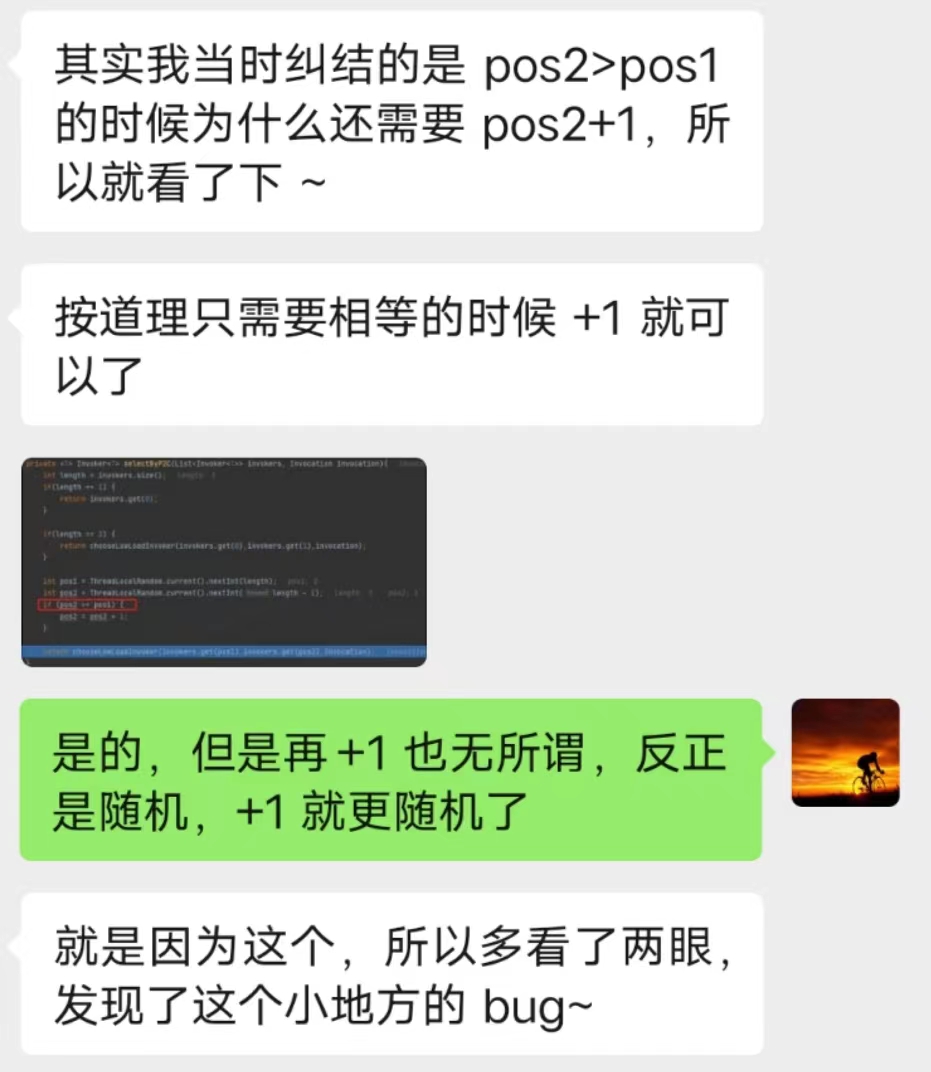
我在回答讀者的時候,也是認為 == 就行了,雖然不公平,但是也不是不能用。
但是經過前面這一波分析。
為什麼一定要是 >=,而不能只是 == 呢?
之前,我一直認為不公平是因為我認為最後一個元素少參與了一次隨機。
但是,由於 >= 的存在,並不會存在這種情況。
啊,為什麼會產生一種讓我想要跪下的感覺?
數學,是因為我在裡面加了數學。
神奇的、令人又上頭又著迷的數學。
荒腔走板
在這個事情上,我整個心態是從自信滿滿到一地雞毛,這個心路歷程讓我想起了我大學的時候,學過的一門課程叫做《線性代數》。
當時我學的可認真,老師講的每節課我感覺我都聽懂了,期末考試的過程中,包括考完之後我都是信心滿滿的樣子,覺得這題也不難啊。
隨隨便便考個八十多分問題不大吧。
最後,考試結果出來的時候我沒及格,我記得是 56 分還是 58 分的樣子,反正差一點點及格,這課居然掛了?
我當時在宿舍就拍案而起:肯定有問題,我要求查卷,我做題的時候很有自信啊。
然後我要到了老師的聯絡方式,並自報家門,說明情況,我堅持認為應該是某個環節出了問題,看看能不能把卷子找出來再看看。
後來啊...
老師把卷子拍照發給我了,確實是某個環節出了問題,這個環節就是我自己。
我和答案對了一下,卷面就只有 40 多分的樣子。
最終成績有 50 多分是因為老師還算了平時分,由上課出勤率和日常作業完成情況綜合算出來的。
那天,我站在宿舍的陽臺上,看著手機上的試卷照片,再挑眼看向遠方,夕陽西下,殘陽如血,六樓的風兒甚至喧囂,肆意的在我臉上拂過。
樓下熙熙攘攘的學生走過,時不時的爆發出一陣陣銀鈴般的笑聲,我只是覺得吵鬧。
隨後,我問室友:什麼時候補考?有沒有人能給我補習一下?
數學,啊,這神奇的、令人又上頭又著迷的數學。