第十四章 其它曲線（Miscellaneous Curves）

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

譯者：池中物王二狗(sheldon)

blog: http://cnblogs.com/willian/

原始碼：github: https://github.com/willian12345/coding-curves

曲線藝術程式設計系列 第十四章

這是系列文章規劃的最後一章。如果後面發現其它有趣的曲線型別可能加在這一章。我原計劃清單裡有幾個主題沒放出來，當然也不排除某天我改主意了。未來額外的內容也可能另起一章加到目錄索引中。

在「最後」一篇， 我想我會講一些隨機曲線，這些曲線不值得單獨開一章來講。還有，我覺得把我從找到公式到編碼的過程完整過一遍會很不錯。

大麻曲線

Weisstein, Eric W "大麻曲線" 來源於網站 https://mathworld.wolfram.com/CannabisCurve.html

Wolfram Mathworld 是一個很好的發掘有趣公式的地方，順便說一句，如果你想發掘更多 2d 曲線，那麼在平面曲線（Plane Curve）這一章節可以深入找找。網站內容很全，還有其它曲線型別可探索。

為什麼選擇大麻曲線？。我只是覺得它很酷（譯者注：本人在此申明我與賭毒不共戴天），僅僅用簡單的相關地數學公式就可以畫出如此複雜的東西。

下面是對應的數學公式：

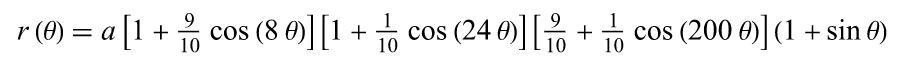
好的，公式有點兒長，但它只是乘法，加法還有一些正弦和餘弦計算。我們可以的。

它定義了一條極座標曲線，這意味著相比於 x, y 的值，我們更關心角度與半徑。我們有個函數 r(θ), θ 是希臘字母，theta。它通常代表角度。當然我們也能猜到 r 代表半徑。所以我們需要一個函數傳入角度得到對應的半徑。

有了角度和半徑，我們很容易計算出用於繪製線段的 x,y 點。組織程式碼後應該像下面在這樣：

for (t = 0; t < 2 * PI; t += 0.01) {
  radius = r(t)
  x = cos(t) * radius
  y = sin(t) * radius
  lineTo(x, y)
}
stroke()

我們通過 t 計算得到半徑，然後再通過半徑和 t 計算得到下一個繪製線條的座標點。

不過事實上來講，r(θ) 除了在這個迴圈內不會在其它任何地方使用，我就直接寫死了。

此處唯一額外要說明的就是需要傳入引數 radius 用 radius 乘以公式。還需要用 x, y 讓曲線居於中心點，所以我們也把它作為引數傳遞（xc 與 yc 代表 x 和 y 中點）。

（譯者注：這裡原作都在 r(t) 計算時用字母小 a 指代除公式之外的部分, 我覺得更難理解更麻煩，小 a 在英語中隨處可見，又不在虛擬碼中明確標出，所以我決定去掉。直接用中文表達出作者原本的意圖）

以下面程式碼作為起點：

function cannabis(xc, yc, radius) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    r = radius * ... // that whole formula. we'll get to it.
    x = cos(t) * r
    y = sin(t) * r
    lineTo(xc + x, yc + y)
  }
  closePath()
}

現在，我們在上面基礎上進行編碼。相當的簡單，我們只需代入公式。分數部分我們使用 0.1 代替 1/10, 0.9 代替 9/10。開始吧！

function cannabis(xc, yc, radius) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    r = radius * (1 + 0.9 * cos(8 * t)) * (1 + 0.1 * cos(24 * t)) * (0.9 + 0.1 * cos(200 * t)) * (1 + sin(t))
    x = cos(t) * r
    y = sin(t) * r
    lineTo(xc + x, yc + y)
  }
  closePath()
}

現在，像下面程式碼這樣看看：

canvas(600, 600)
cannabis(300, 300, 140)
stroke()

That gives me this image:

這會得到如下圖：

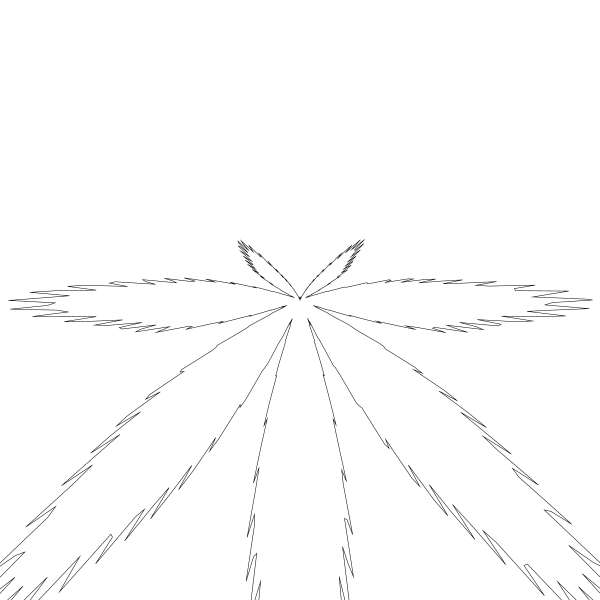
Ah, 好的，有點兒東西。

首先，此公式使用笛卡爾座標系，而我用的是上下相反的螢幕座標系。所以我需要把 y 軸翻轉。問題不大。

接著，中心點是所有「葉子」連線點。所以在翻轉後，我可以將中心點設定在 canvas 靠近底部的位置。

最後，我猜 140 會是一個不錯的半徑值，它會將繪製出的圖形限制在 600X600 大小的 canvas 內。事實上，我期望的是把圖形限制在 canvas 大小的一半。但實際上大的葉子超出一部分也不影響。我們可以在程式碼中修復它，比如將半徑乘以某些小數讓大的葉子半徑降下來。我就不做這部分限制了，我假裝自己只會傳合適的值，相關限制程式碼你自己可以搞定的。

function cannabis(xc, yc, radius) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    r = radius * (1 + 0.9 * cos(8 * t)) * (1 + 0.1 * cos(24 * t)) * (0.9 + 0.1 * cos(200 * t)) * (1 + sin(t))
    x = cos(t) * r
    y = sin(t) * r
    lineTo(xc + x, yc - y)
  }
  closePath()
}

我所做的只是將 lineTo 這一行用yc + y 代替了 yc - y 。

在呼叫函數時引數也調整了一下（經過試錯後得出還不錯的引數值）

canvas(600, 600)
cannabis(300, 520, 120)
stroke()

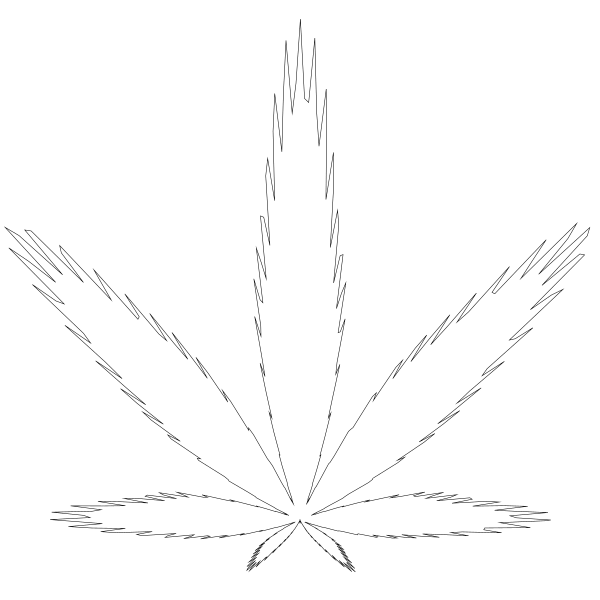
結果還闊以！

提醒一下。我經過仔細考慮調整了 canvas 的大小，這樣 yc 引數值可以設定到 420。 你調不調的隨你