兩種常用的存圖方法(鄰接矩陣和鏈式前向星)

　　今天上午模擬賽的時候，（十分錯誤地）判斷有一道題可以用LCA混點分（然而還不如直接爆搜得分高），在敲那個LCA的程式碼時突然想起來我好像還沒有寫過LCA，想了想，是該給我的LCA寫點東西了呢。

　　但是！不出意外的，出了億點點意外，就是我在敲板子題的時候發現經過一年的荒廢，我已經完全不會鏈式前向星。好不容易搗鼓了半天，終於還是沒調出來，於是我只能十分痛心疾首地去好好學習了一下。

　　所以！本來今天要說說LCA的，但是最終我決定還是先講講圖論最最基礎，也是最為致命（啊，就是說我因為不會鏈式前向星導致我沒把LCA整出來）的東西之一，存圖！

　　這裡只介紹兩種常用的方法，如有需要的的同學可以看看別人的拓展。

--------------------------------------分割線---------------------------------------------

一，鄰接矩陣

　　鄰接矩陣顧名思義，是一個矩陣（廢話），在老一點的演演算法書裡面常常能見到用這種方法存圖的程式碼。優點是特別簡單好理解，用起來也是非常的方便；缺點在於空間複雜度是n^2級的。

　　舉個例子吧，有如下無向連通圖（每邊邊長為1）

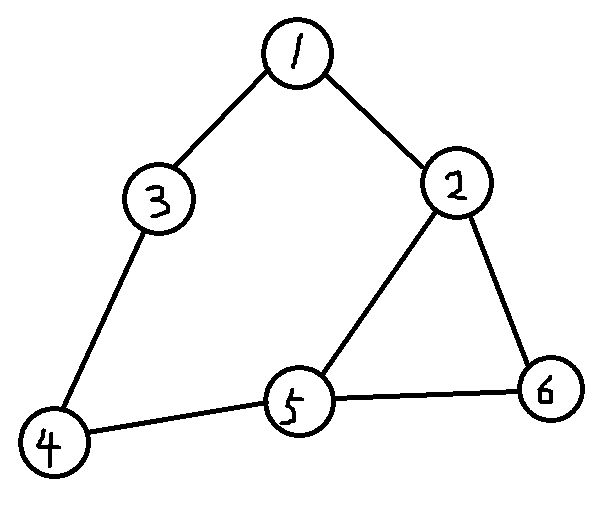
　　首先我們要開一個陣列f[mm][mm]，其中f[i][j]表示點i到點j之間連邊的長度，如下圖

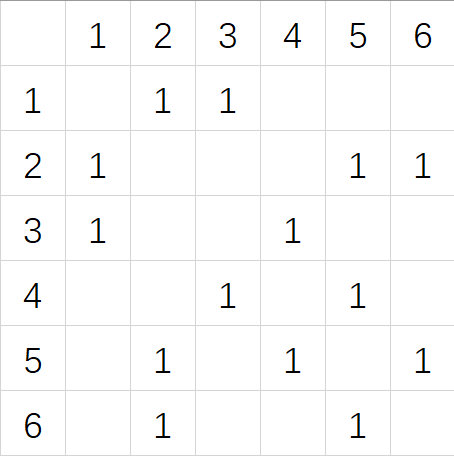　　　　另外，很顯然一個點到它自己的距離是零

　　因為這是一個無向圖，所以存圖的時候要注意f[i][j]=f[j][i]這一點，即，同一邊要存兩次；

　　如果說點i和點j之間沒有直接的邊那應該如何表示呢？很簡單，初始化為inf，兩個點之間距離無限遠不就是說兩點之間不能互相直接到達嗎，所以見如下程式碼

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int mm=205;//並沒有什麼特殊意義
 4 const int inf=1e9+7;
 5 int f[mm][mm];
 6 int n,m;//有n個點，m條邊 
 7 int main()
 8 {
 9     cin>>n>>m;
10     for(int i=1;i<=n;i++)
11     for(int j=1;j<=n;j++)
12     {
13         f[i][j]=inf;//初始化為任意兩點之間距離為inf 
14      } 
15     for(int i=1;i<=m;i++)
16     {
17         int x,y;
18         cin>>x>>y;//將兩個點相連 
19         f[x][y]=1;
20         f[y][x]=1;
21      } 
22     return 0;
23 }

二、鏈式前向星

　　鏈式前向星近些年非常常見，它的誕生讓圖論題的資料範圍大幅提高（真是太糟糕了），相比於鄰接矩陣，鏈式前向星確實會更復雜、更難自己想（指的是我自己調半天都不知道問題在哪），但一個標準的鏈式前向星的程式碼量其實很少，佔用的空間也會少得多

　　鄰接矩陣實際上是基於點的存圖，它儲存的是點與點之間的連邊，而鏈式前向星是基於邊的存圖，它儲存的是一條條的邊，每條邊的兩個端點分起點終點。

　　我們選擇使用結構體（結構體介紹：https://www.cnblogs.com/qj-Network-Box/p/13138534.html）來實現存邊的操作，一條邊的要素，無非是起點終點和長度，由於上圖每條邊的長度一樣，暫時先不考慮長度的問題

1 const int mm=205;//沒有什麼特別的意義 
2 struct node{
3     int s,v;//從點s到點v 
4 }a[mm];

　　很顯然，鏈式前向星，身為一個用鏈開頭的詞，和連結串列多多少少有點聯絡

　　而這個聯絡就在於：同一起點的邊被排成一條鏈。原因很顯然，方便查詢

　　我們回到這幅圖

　　按照起點分類，可以變成以下幾串

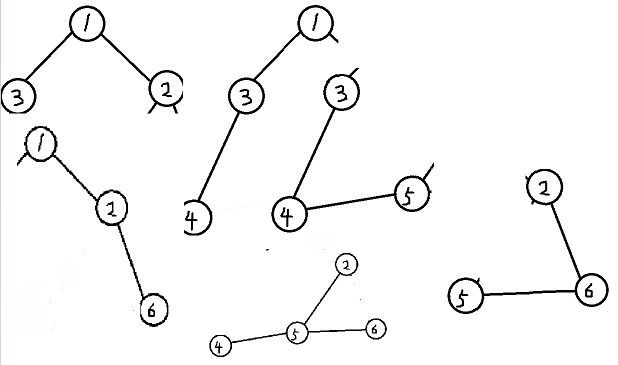
　　比如，要實現查詢到點1到點2的路徑後能找到點1到點3的路徑，就可以在存點1到點2路徑的結構體裡面新增一個nex元素，nex指向下一個以1為起點的元素

　　那麼問題來了，我們一開始怎麼找到點1到點2的那條邊呢（身為該起點被存入的第一條邊，沒有nex指向它），我們需要一個head[x]陣列來儲存起點為x的第一條邊的序號

　　顯然既然是同一起點的，在存邊的時候就不需要把起點算進去了

const int mm=205;//沒有什麼特別的意義 
struct node{
    int v,nex;
}a[mm*2];
int head[mm];//用於儲存最頭部邊的序號

　　考慮遍歷，以x為起點的第一條邊編號為head[x],下一條就應該是a[head[x]].nex,再下一條就是a[a[head[x]].nex].nex，直到某個節點的nex指向0

　　程式碼實現如下

#include<bits/stdc++.h>
using namespace std;
int tot;
int n; 
const int mm=205;//沒有什麼特別的意義 
struct node{
    int v,nex;//從點x到點v 
}a[mm*2];
int head[mm];//用於儲存第一條邊的序號 
void add(int x,int y) //一條x到y的邊
{
    a[++tot].v=y;//目標是y
    a[tot].nex=head[x];//將上一條邊的nex指向這一條邊
    head[x]=tot;//更新 
} 
void pp(int x)
{
    for(int i=head[x];i!=0;i=a[i].nex)//以head[x]為第一邊，每次跳轉到nex所指的下一條邊 
    {
        cout<<x<<" "<<a[i].v<<endl;//輸出起點和終點 
    }
    return ;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int x,y;
        cin>>x>>y;
        add(x,y),add(y,x);//無向圖要存兩邊 
    }
    for(int i=1;i<=n;i++)//輸出所有的邊 
    {
        pp(i);
    }
    return 0;
}