「學習筆記」基環樹
2023-06-27 21:00:43
眾所周知,一棵有 \(n\) 個節點的樹有 \(n - 1\) 條邊,樹上沒有環。
據此,明顯的,對於一個有 \(n\) 個結點 \(n\) 條邊的無向連通圖,必定是在一棵樹上的任意兩個節點之間連一條邊構成的。我們把 \(n\) 個節點 \(n\) 條邊的無向連通圖,就稱為基環樹。
基環樹上存在環,因此基環樹它不是樹,而是圖。基環樹又稱章魚圖。

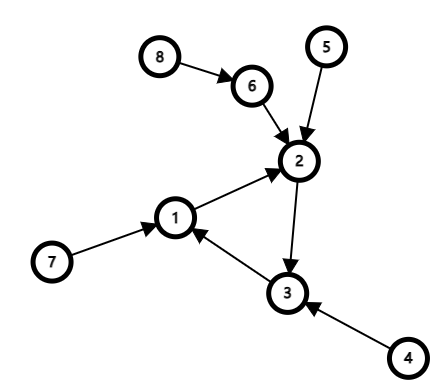
如圖,這就是一棵基環樹。
如果一張有向弱連通圖每個點的入度都為 \(1\),則稱它是一棵 基環外向樹,如下圖。

如果一張有向弱連通圖每個點的出度都為 \(1\),則稱它是一棵 基環內向樹,如下圖。
多棵樹可以組成一個森林,多棵基環樹可以組成基環森林,多棵基環外向樹可以組成基環外向樹森林,多棵基環內向樹可以組成基環內向森林。
找環
基環樹的的特別之處就在於這個環,因此,大部分基環樹題目中,找環是十分必要的。
在簡單圖中,可以利用 dfs 的天然棧性質來找環,具體實現方式與 tarjan 求強連通分量很相似。
void getloop(int u) {
dep[u] = dep[fa[u]] + 1;
for (int v : e[u]) {
if (v == fa[u]) continue ;
if (!dep[v]) {
fa[v] = u;
getloop(v);
}
else if (dep[v] < dep[u]) {
for (int i = u; ; i = fa[i]) {
ok[i] = 1;
loop[++ m] = i;
if (i == v) {
break;
}
}
}
}
}
再有重邊的圖中,需要做一下小小的處理,與 tarjan 求雙連通分量很像,記錄一下邊的編號,只要不走回剛走過來的邊就行。
vector<pair<int, int> > e[N];
void getloop(int u, int i) {
dep[u] = dep[fa[u]] + 1;
for (auto it : e[u]) {
int v = it.first, k = it.second;
if (k == i) continue;
if (!dep[v]) {
fa[v] = u;
getloop(v, k);
}
else if (dep[v] < dep[u]) {
for (int j = u; ; j = fa[j]) {
ok[j] = 1;
loop[++ m] = j;
if (i == v) {
break;
}
}
}
}
}
練習
基環樹題目中,較常見的 套路 思路就是先將環去掉,對每一棵樹做處理,最後再對環做處理。
P8943 Deception Point
這是一道基礎的入門題。
我們發現,只要兩個人能在到達環上之前不碰面(包括剛到達環上),那雷切爾就一定存活 秦王繞柱,否則就必死無疑,處理三角洲到達環上的距離與雷切爾到達環上的距離,再檢視是否會在到達環上是碰面即可。
/*
The code was written by yifan, and yifan is neutral!!!
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 2e5 + 5;
int n, q, m;
int dep[N], top[N], fa[N], loop[N], dis[N];
bool ok[N];
vector<int> e[N];
void getloop(int u) {
dep[u] = dep[fa[u]] + 1;
for (int v : e[u]) {
if (v == fa[u]) continue ;
if (!dep[v]) {
fa[v] = u;
getloop(v);
}
else if (dep[v] < dep[u]) {
for (int i = u; ; i = fa[i]) {
ok[i] = 1;
loop[++ m] = i;
if (i == v) break;
}
}
}
}
void dfs(int u, int fat, int tp) {
top[u] = tp;
for (int v : e[u]) {
if (v == fat || ok[v]) continue ;
dep[v] = dep[u] + 1;
dfs(v, u, tp);
}
}
int main() {
n = read<int>(), q = read<int>();
for (int i = 1, x, y; i <= n; ++ i) {
x = read<int>(), y = read<int>();
e[x].emplace_back(y);
e[y].emplace_back(x);
}
getloop(1);
memset(dep, 0, sizeof dep);
for (int i = 1; i <= m; ++ i) {
dfs(loop[i], 0, i);
// cout << loop[i] << ' ';
}
while (q --) {
int x = read<int>(), y = read<int>();
int d1 = dep[x], t1 = top[x];
int d2 = dep[y], t2 = top[y];
if (d2 + min(abs(t1 - t2), m - abs(t1 - t2)) > d1) {
puts("Survive");
}
else {
puts("Deception");
}
}
return 0;
}
P8655 [藍橋杯 2017 國 B] 發現環
簡單的找環模板 = =||
/*
The code was written by yifan, and yifan is neutral!!!
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 1e5 + 5;
int n;
int dep[N], fa[N];
bool ok[N];
vector<int> e[N];
void getloop(int u) {
dep[u] = dep[fa[u]] + 1;
for (int v : e[u]) {
if (v == fa[u]) continue;
if (!dep[v]) {
fa[v] = u;
getloop(v);
}
else if (dep[v] < dep[u]) {
for (int i = u; ; i = fa[i]) {
ok[i] = 1;
if (i == v) break;
}
}
}
}
int main() {
n = read<int>();
for (int i = 1, x, y; i <= n; ++ i) {
x = read<int>(), y = read<int>();
e[x].emplace_back(y);
e[y].emplace_back(x);
}
getloop(1);
for (int i = 1; i <= n; ++ i) {
if (ok[i]) {
printf("%d ", i);
}
}
return 0;
}
P6037 Ryoku 的探索
樸素做法為 \(O_{n^2}\) 的。
但仔細觀察,就會發現,最終答案一定是除去環上一條邊,其他邊的長度總和,刪掉哪條邊呢?根據美觀度來判斷。
/*
The code was written by yifan, and yifan is neutral!!!
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 1e6 + 5;
int n, m;
ll ans, sum;
int loop[N], top[N], fa[N], dep[N];
ll dis[N];
bool ok[N];
struct node {
int v;
ll w, p;
node(int a, ll b, ll c): v(a), w(b), p(c) {};
};
vector<node> e[N];
void getloop(int u) {
dep[u] = dep[fa[u]] + 1;
for (node it : e[u]) {
int v = it.v;
if (v == fa[u]) continue;
if (!dep[v]) {
fa[v] = u;
getloop(v);
}
else if (dep[v] < dep[u]) {
for (int i = u; ; i = fa[i]) {
ok[i] = 1;
loop[++ m] = i;
if (i == v) break;
}
}
}
}
void dfs(int u, int fat, int tp) {
top[u] = tp;
for (node it : e[u]) {
int v = it.v;
ll w = it.w;
if (v == fat || ok[v]) continue;
ans += w;
dfs(v, u, tp);
}
}
int main() {
n = read<int>();
for (int i = 1, x, y; i <= n; ++ i) {
x = read<int>(), y = read<int>();
ll w = read<ll>(), q = read<ll>();
e[x].emplace_back(y, w, q);
e[y].emplace_back(x, w, q);
}
getloop(1);
for (int i = 1; i <= m; ++ i) {
dfs(loop[i], 0, loop[i]);
}
loop[m + 1] = loop[1];
for (int i = 1; i <= m; ++ i) {
for (node it : e[loop[i]]) {
int v = it.v;
if (v == loop[i + 1]) {
dis[i] = it.w;
sum += it.w;
break;
}
}
}
for (int i = 1, u; i <= n; ++ i) {
u = top[i];
ll W = 0, P = 1e9;
for (node it : e[u]) {
int v = it.v;
ll w = it.w, p = it.p;
if (!ok[v]) continue;
if (p < P) {
W = w;
P = p;
}
}
printf("%lld\n", sum - W + ans);
}
return 0;
}
朝氣蓬勃 後生可畏