曲線藝術程式設計 coding curves 第十二章 超級橢圓與超級方程(Superellipses and Superformulas)
第十三章 超級橢圓與超級方程(Superellipses and Superformulas)
原作:Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/
譯者:池中物王二狗(sheldon)
原始碼:github: https://github.com/willian12345/coding-curves
曲線藝術程式設計系列 第十三章

在這一章我們將討論一些有趣的圖形。超級橢圓在設計與UI領域非常有用, 有一種特別的超級橢圓被親切的稱為「方圓形」. 一種介於正方形和圓形之間的幾何形狀,四個角為圓角,邊緣呈現出圓潤的曲線。 超級方程是超級橢圓的一個擴充套件。它更復雜,也許沒那麼有用,但它自身足夠有趣。讓我們開始探索吧。
超級橢圓 (Superellipses)
有時候你可能需要繪製矩形。這個需求太常見了。在任何圖形庫中都會有繪製矩形的方法。

但光是矩形看起來比較無聊。四角都有點兒。。方。 你很自然的想要圓角矩形。有些繪圖 api 也有繪製圓角矩形的方法,但我們直接手搓一個也不難。在四個角都繪製一個 90 度的 圓弧,並將它們連起來就是圓角矩形了。

事實上,你可以讓四個角擁有相對小的半徑,這樣它看起來會更圓

但你應該不會喜歡這樣做。某種程度上講是對連續邊界的打斷。一開始都是漂亮的直線,到邊角突然又要使用 arc 這種操作。你也許想在圓角處變化的更自然順滑。
還是得看超橢圓啊。
你可以想象超級橢圓是介於橢圓和矩形的混合體。就像橢圓和其它曲線一樣在本系列中,我們認為這個形狀擁有一箇中心點和變化的半徑 t 從 0 至 2*PI。這有別於大部分矩形方法,矩形方法往往用 x,y 為座標(通常是矩形的 left 和 top 值),還有 width,height。 但你可以按你自己的想法調整此方法。
在數學上有好幾種方法用於表達超級橢圓。我們不停的尋找直到找到下面這個可對 t 進行引數化的公式:
x = pow(abs(cos(t)), 2 / n) * a * sign(cos(t))
y = pow(abs(sin(t)), 2/ n) * b * sign(sin(t))
Hmm... 比你預想的要複雜吧?
這裡有個簡介的公式像這樣:
x = pow(cos(t), 2 / n) * a
y = pow(sin(t), 2 / n) * b
但問題在於,此函數只能處理 1/4: 0 到 PI / 2。相比於為每個角跑4次迴圈, 並計算出 x 和 y,我們用一些好用的數學方法 abs 和 sign 直接計算。
你使用的語言平臺一定也有個 abs 方法,它只是直接返回了絕對值。你可以自己簡單動手寫一個你自己的:
function abs(val) {
if (val < 0) {
return -val
}
return val
}
這個函數總是會返回 0 或正數。
儘管你可能沒有 sign 函數。sign 方法傳入負數 返回 -1, 傳入 正數 返回 +1。 傳入 0 返回 0。可以像下面這樣實現 sign 函數
function sign(val) {
if (val < 0) {
return -1
}
if (val > 0) {
return 1
}
return 0
}
你可能躍躍欲試像下面這樣寫:
function sign(val) {
return val / abs(val)
}
這個函數工作的很完美。直到 val 值為 0 時它崩潰了。為了防止崩潰你得進行一下條件判斷。
在上面的公式中,程式碼有些重複或者變數不太清晰的,並且沒有用於設定形狀位置方法。下面這個函數才是比較有用的:
function superellipse(xc, yc, rx, ry, n) {
for (t = 0; t < PI * 2; t += 0.01) {
c = cos(t)
s = sin(t)
x = pow(abs(c), 2 / n) * rx * sign(c)
y = pow(abs(s), 2 / n) * ry * sign(s)
lineTo(xc + x, yc + y)
}
closePath()
}
大多數路徑繪製 api 有 closePath 這樣的方法用於最終閉合路徑。
好了。讓我們用新的超級橢圓重寫最開始的圓角矩形。
width = 600
height = 400
canvas(width, height)
// set color to orange however you do that...
// 把顏色設定為桔色,無論你用怎樣的方式
superellipse(300, 200, 250, 150, 10)
fill()

相比於簡單的實現圓角矩形,你有可能不喜歡這樣複雜的程式碼, 但讓我們繼續深入探索一下。
最後一個引數 n 值,控制著圓角的曲度。值越高,它越接近於矩形。這是 n 為 20 時:

這是 n 為 4 時:

它看起來像是老式電視機的螢幕形狀。
是時候祭出方圓 squirecles 了。
方圓 (Squircle)
一個超級橢圓的 x 和 y 半徑相等則被稱為超級圓。也被稱為方圓。由方和圓組合而成。 一些方圓的狀態定義 n 必須為 4。 它看起來會像下圖:

這個形狀看起來就舒適多了, 而且最近在 UI 設定界也很流行. 它經常被用於 icon 設計, 特別多用於手機裝置 app 的啟動圖示。有時候 n 值不完全是 4 就像上面那樣,但非常接近。
這裡有一些方圓公式的變種,由 John Cook 編寫 https://www.johndcook.com/blog/2022/10/27/variant-squircle/。 順便說一句它的網站也是相當好的學習資源。我不能說完全理解他講的,但它確實啟發了我探索各種有趣的方法。
讓我們回到超級橢圓。
再看看引數 n。 我們已經知道了引數 n 越大,圓角越小。當 n 為 2 時, 有趣的來了。我們直接得到了一個橢圓(或一個圓,如果寬高相等的話)。


當 n 從 2 降到 1 時,我們可以看到圓邊開始轉變為角了,並且角變的更直了。 下圖是 n 設為 1.5:

當 n = 1 ,我們直接得到了鑽石形(菱形)。

n 繼續減小,四個角開始向內彎曲,下圖是 0.75

當為 0.2 時,超級橢圓幾乎消失了。

當 n 值越來越小時本質上圖形確實會消失不見。
但當 n 為負數時,事情變的更詭異了。 下面是 n 為 -4 時。我不得不將 整個圖弄的小一點,以便讓你能看到發生了啥 -- 我們得到了一個填充矩形,超出各個角翻轉的超級橢圓。

我不確定最後一部分具體有啥用,但效果就是這樣。
這就是超級橢圓。在你的圖形工具庫裡它會很有用。讓我們繼續往下看。
超級公式(Superformulas)
超級公式廣義的或者說是超級橢圓的擴充套件。再一次,半徑從 0 到 2*PI 時會變化。半徑的方程如下:
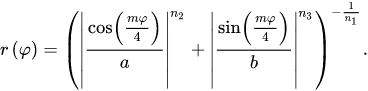
這方程是直接從維基百科上拿的。這比自己用鍵盤打出來要容易的多了。需要把它們轉換成虛擬碼公式,但你應該可以 看到這個公式與超級橢圓很類似。你可以看到,我們從 cosine 和 sine 得到值後再除以某個值,再對其取絕對值後進行乘方。彎彎曲曲的符號是希臘字母 phi, 我們把它稱為 t 。 所以 我們可以這樣說角度 t 上的半徑值是...
我們還有一些其它的變數, m, n1, n2 和 n3 還有 a 和 b 它們會影響 x 和 y 半徑。在我的實現中我將其簡化成一個半徑。所以我將設定 a 和 b 為 1, 這意為著程式碼中我們可以將其忽略掉並將結果與我們想要的半徑相乘。
當然,這還是挺複雜的,我們將這些變數分步計算實現,最後組合在一起。
首先,傳入同樣的值給 cosine 與 sine 計算, 這樣就可以預計算它們。我將稱其為 m 對稱。
angle = symmetry * t / 4
然後大的圓括號之間還有兩項需要新增上。我們將兩項都計算出來:
term1 = pow(abs(cos(angle), n2)
term2 = pow(abs(sin(angle), n3)
再強調一次,我們將 a 和 b 假設為 1, 這樣就可以忽略它們了。
接下來,我們把這些項結合到最後的公式裡得到最終的半徑值。 記住我們需要乘以總的半徑:
r = pow(term1 + term2, -1/n1) * radius
最後,用半徑與角度得到下一個繪製點的位置:
x = xc + cos(t) * r
y = yc + sin(t) * r
全部合在一起後得到下面的方法:
function superformula(xc, yc, radius, symmetry, n1, n2, n3) {
for (t = 0; t < 2 * PI; t += 0.01) {
angle = symmetry * t / 4
term1 = pow(abs(cos(angle), n2)
term2 = pow(abs(sin(angle), n3)
r = pow(term1 + term2, -1/n1) * radius
x = xc + cos(t) * r
y = yc + sin(t) * r
lineTo(x, y)
}
closePath()
}
好了, 我們能拿這一坨做什麼呢?這些引數分別用來控制什麼?
當我面對類似這樣的程式碼時,我通常先找到有簡單聯絡且固定的引數,看看這個引數到底改變的是什麼。然後再看另一個引數,最後再看可變引數的影響。幸運的是,超級公式的維基百科頁面給了我們很好的圖示,我們可以從這點入手:
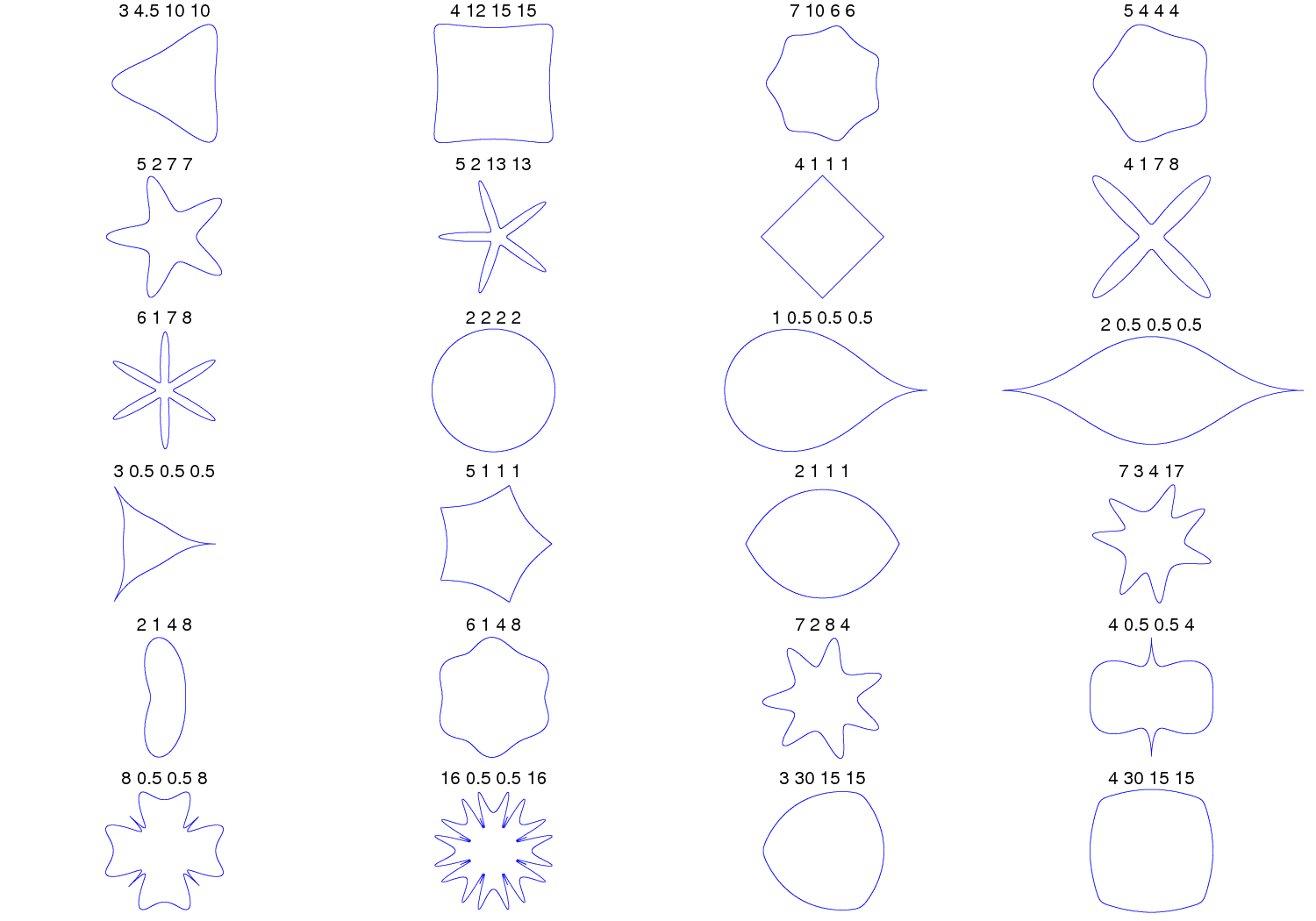
上圖中的每張圖代表著四個不同引數數值 m(也被稱為對稱), n1, n2 和 n3。
下圖是 對稱為 3, 所有 n 引數設為 1 的結果:

這是對稱為 5:

這是對稱為 8:

現在保持稱為 8, 讓我們把 n1 設為 10:

n1 降到 3:

再到 1 以下,降到 0.2:

所以由此得知 n1 用來控制形狀各個邊的凹凸。
好的,現在我們將 m 固定為 8 把 n1 調回到 1。然後將 n2 升至 1.5:

仍然得到了 8 個節點, 間隔的節點有點兒圓,間隔之間的節點有點兒尖。讓它更明顯一點,設 n2 = 2:

當 n2 = 5, 圓角節點開始翻倍了,尖角節點漸漸降低了

下圖是 n2 = 10。我不得不將半徑減小,因為形狀超出 canvas 邊界了:

最後,將 n1 和 n2 都變回 1,我們試試將 n3 設為 3:

它和引數 n2 的影響差不多,只是節點是相反的變化,有點兒像整個形狀轉了 45 度。
到這裡,已經清楚這幾個引數的作用了,試試給這幾個引數隨機值:
m=16, n1=0.5, n2=0.75, n3=2

m=32, n1=0.9, n2=0.2, n3=-0.3

當然你不用像我這樣設定隨機引數。你自己試試用不同的值。可以用大的數,小的數,小數,負數,質數,能被其它引數整數或不能整的數。看看會發生什麼。
你應該記得,我們把 a 和 b 從原公式中去掉了用了單一的半徑。你也許想把它們重加入公式用於建立橢圓的超級公式。維基百科中也給了,把 m 分成 y 和 z:
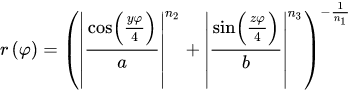
這允許你可以建立更復雜的形狀。
我試著用不同的引數建立形狀,下圖是我建立出的比較喜歡的一個:

我把它作為課後練習留給讀者實現。
本章 Javascript 原始碼 https://github.com/willian12345/coding-curves/blob/main/examples/ch13
部落格園: http://cnblogs.com/willian/
github: https://github.com/willian12345/