本文由gpt4輔助撰寫（gptschools.cn）

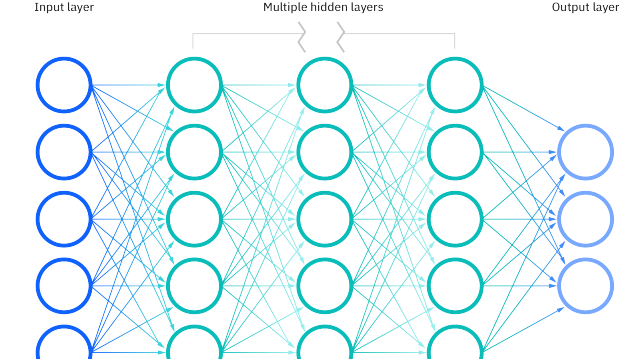
神經網路是一種模仿人腦神經元工作原理的計算模型，用於實現機器學習和人工智慧系統。它由一系列相互連線的神經元（也稱為節點或單元）組成，這些神經元組織成不同的層。神經網路通常包括輸入層、一個或多個隱藏層和輸出層。每個節點根據其輸入資料和相應的權重計算輸出值，並通過啟用函數進行非線性轉換。

神經網路可以通過學習和調整權重實現自適應，從而在處理複雜問題（如影象識別、自然語言處理和遊戲策略等）時具有很高的靈活性。訓練神經網路的過程通常包括使用大量輸入資料和期望輸出，計算損失函數（用於衡量網路輸出與期望輸出之間的差距），並使用優化演演算法（如梯度下降法）調整權重以最小化損失。

神經網路是深度學習的核心組成部分，深度學習模型通常包含多個隱藏層，從而能夠學習更復雜數學表示和抽象概念。

下面以一個簡單的神經網路（用於解決 XOR 問題）為例，說明神經網路中的各個概念。

該神經網路範例中，包含一個輸入層（2個節點），一個隱藏層（2個節點）和一個輸出層（1個節點）。輸入輸出層之間以及隱藏層與輸出層之間的所有節點均相互連線。啟用函數為 Sigmoid 函數。

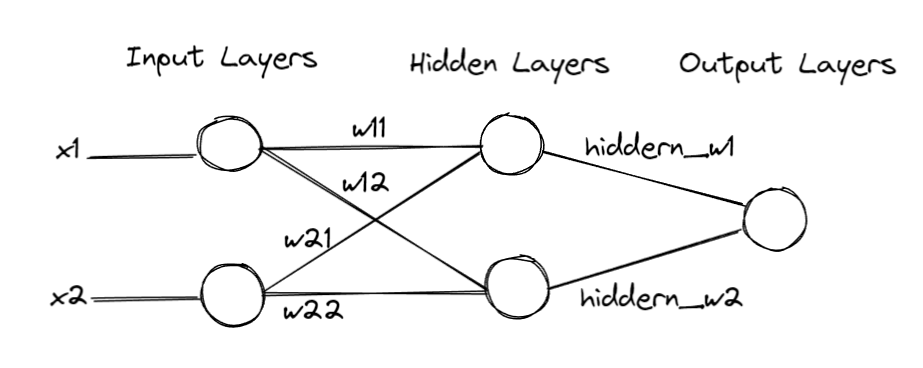
上述神經網路的python實現如下：

import numpy as np

# Sigmoid 啟用函數
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 使用 sigmoid 導數進行非線性變換以及反向傳播計算梯度
def sigmoid_derivative(x):
    return x * (1 - x)

def mse_loss(y_true, y_pred):
    return np.mean(np.square(y_true - y_pred))

class NeuralNetwork:
    def __init__(self, input_nodes, hidden_nodes, output_nodes):
        self.input_nodes = input_nodes
        self.hidden_nodes = hidden_nodes
        self.output_nodes = output_nodes
        self.weights_ih = np.random.rand(self.input_nodes, self.hidden_nodes) - 0.5
        self.weights_ho = np.random.rand(self.hidden_nodes, self.output_nodes) - 0.5
        self.bias_h = np.random.rand(1, self.hidden_nodes) - 0.5
        self.bias_o = np.random.rand(1, self.output_nodes) - 0.5

    def feedforward(self, input_data):
        hidden = sigmoid(np.dot(input_data, self.weights_ih) + self.bias_h)
        output = sigmoid(np.dot(hidden, self.weights_ho) + self.bias_o)
        return hidden, output

    def backward(self, input_data, hidden, output, target_data, learning_rate=0.1):
        # 計算損失函數的梯度
        output_error = target_data - output
        output_delta = output_error * sigmoid_derivative(output)

        hidden_error = np.dot(output_delta, self.weights_ho.T)
        hidden_delta = hidden_error * sigmoid_derivative(hidden)

        self.weights_ho += learning_rate * np.dot(hidden.T, output_delta)
        self.weights_ih += learning_rate * np.dot(input_data.T, hidden_delta)
        self.bias_o += learning_rate * np.sum(output_delta, axis=0)
        self.bias_h += learning_rate * np.sum(hidden_delta, axis=0)

    # 根據輸入輸出資料，訓練多輪，更新神經網路的權重和偏置，最終得到正確的神經網路引數
    def train(self, input_data, target_data, epochs, learning_rate=0.5):
        for _ in range(epochs):
            hidden, output = self.feedforward(input_data)
            self.backward(input_data, hidden, output, target_data, learning_rate)

if __name__ == "__main__":
    # 範例
    X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    Y = np.array([[0], [1], [1], [0]])

    nn = NeuralNetwork(input_nodes=2, hidden_nodes=2, output_nodes=1)

    print("Before training:")
    _, output = nn.feedforward(X)
    print(output)

    nn.train(X, Y, epochs=2000, learning_rate=0.8)

    print("After training:")
    _, output = nn.feedforward(X)
    print(output)

    # 計算損失
    loss = mse_loss(Y, output)
    print("Loss:", loss)

首先，建立 XOR 問題的輸入和輸出資料集，分別儲存在 NumPy 陣列中
初始化權重與偏置
然後，根據輸入輸出資料，訓練2000輪
每輪訓練都會通過反向傳播更新各層的權重和偏置，最終得到正確的神經網路引數

上述簡單範例中，涉及到如下神經網路基本概念：

前向傳播：利用若干個權重係數矩陣W,偏倚向量b來和輸入值向量x進行一系列線性運算和啟用運算，從輸入層開始，一層層的向後計算，一直到運算到輸出層，得到輸出結果為值
啟用函數:（Activation Function）是一種在神經網路中使用的非線性函數，用於將神經元的累積輸入值轉換為輸出值。啟用函數的主要目的是引入非線性特性，使得神經網路能夠學習並表示複雜的資料模式。如果沒有啟用函數，神經網路將僅僅是一個線性迴歸模型，無法處理複雜的問題。
反向傳播：核心思想是通過優化權重與偏置，從而逐漸減小預測輸出與真實值之間的差距，提高神經網路的效能。反向傳播過程開始於計算輸出層的誤差，即預測輸出與實際目標之間的差值。然後，這個誤差將從輸出層向後傳播到隱藏層。為了更新神經網路中的權重，我們需要計算損失函數相對於每個權重的梯度。我們使用鏈式法則（chain rule）將這些梯度分解為前一層的輸出、當前層的梯度和後一層的梯度。通過這種方式，我們可以得到每個權重的梯度，並用它們更新權重以最小化損失。
損失函數：損失函數值在訓練過程中起到的作用是衡量模型預測結果與實際目標值之間的差距。在反向傳播過程中，我們實際上是通過損失函數的梯度來調整神經網路的權重和偏置，從而使得損失值最小化。

在上面的程式碼範例中，我們計算了輸出層的誤差（output_error），這個誤差實際上就是損失函數的梯度。這裡的損失函數是均方誤差（MSE），計算梯度的公式為：

output_error = target_data - output

在反向傳播過程中，我們通過該梯度來更新權重和偏置，以使得損失值最小化。因此，損失值在訓練過程中起到了關鍵作用。

其中，Sigmoid 函數是一種常用的啟用函數，用於神經網路中對節點輸出進行非線性轉換。Sigmoid 函數的數學表示式如下：

sigmoid(x) = 1 / (1 + e^(-x))

其中，x 是輸入值，e 是自然常數（約等於 2.71828）。

Sigmoid 函數的輸出值範圍在 0 和 1 之間，具有平滑的 S 形曲線。當輸入值 x 趨向於正無窮大時，函數值接近 1；當輸入值 x 趨向於負無窮大時，函數值接近 0。因此，Sigmoid 函數可以將任意實數輸入對映到 (0, 1) 區間內，使得網路輸出具有更好的解釋性。此外，Sigmoid 函數的導數也可以方便地用其函數值表示，便於進行梯度下降優化演演算法。

然而，Sigmoid 函數也存在一些問題，例如梯度消失問題。當輸入值過大或過小時，Sigmoid 函數的梯度（導數）接近於 0，導致權重更新非常緩慢，從而影響訓練速度和效果。因此，在深度學習中，有時會選擇其他啟用函數，如 ReLU（線性整流單元）等。

另外，偏置（bias）的引入是為了增加模型的表達能力。具體來說，在 Sigmoid 啟用函數中，偏置的作用如下：

調整啟用函數的輸出：在神經網路中，啟用函數（如 Sigmoid 函數）用於對節點的線性加權和進行非線性轉換。偏置相當於一個常數值，可以使得啟用函數的輸出在整體上向上或向下平移。這樣，啟用函數可以在不同區域內保持對輸入的敏感性，提高模型的擬合能力。
提高模型的靈活性：加入偏置後，神經網路可以學習到更復雜的表示。偏置引數使神經網路能夠在沒有輸入（或輸入為零）時產生非零輸出。如果沒有偏置，即使權重引數不同，神經元在輸入為零時的輸出也將相同。因此，引入偏置為神經網路提供了額外的自由度，使其能夠更好地擬合複雜的資料。

以 Sigmoid 函數為例，一個神經元的輸出可以表示為：

output = sigmoid(w1 * x1 + w2 * x2 + ... + wn * xn + b)

這裡，w1、w2、...、wn 是輸入資料（x1、x2、...、xn）對應的權重，b 是偏置。通過調整偏置 b 的值，可以使 Sigmoid 函數的輸出整體上升或下降，從而改變神經元的啟用閾值。這使神經網路能夠更好地適應不同的資料分佈，提高模型的泛化能力。

FAQs

梯度與函數導數的關係？

梯度與導數密切相關，但它們有一些區別。對於單變數函數（即只有一個自變數的函數），梯度就是導數。導數表示該函數在某一點處的切線斜率。對於多變數函數（即有多個自變數的函數），梯度是一個向量，包含了函數在某一點處沿著各個座標軸方向的偏導數。

換句話說，梯度是一個向量，它將多個偏導陣列合在一起，描述了多變數函數在各個方向上的變化情況。梯度的方向是函數在該點處變化最快的方向，梯度的大小表示函數在該點處的變化速率。

總結一下：

對於單變數函數，梯度就是導數。
對於多變數函數，梯度是一個包含所有偏導數的向量。

AI Advisor公眾號:

什麼是神經網路？用程式碼範例解析其工作原理

參考