SPSS統計教學：卡方檢驗

本文簡要的介紹了卡方分佈、卡方概率密度函數和卡方檢驗，並通過SPSS實現了一個卡方檢驗例子，不僅對結果進行了解釋，而且還給出了卡方、自由度和漸近顯著性的計算過程。本文用到的資料"2.2.sav"連結為: https://url39.ctfile.com/f/2501739-875711187-f3dbb8?p=2096 (存取密碼: 2096)

一.卡方分佈
卡方分佈是一種概率分佈，若\(k\)個隨機變數\(Z_1、......、Z_k\)是相互獨立且符合標準正態分佈的隨機變數（數學期望為0、方差為1），那麼隨機變數\(Z\)的平方和\(X = \sum\limits_{i = 1}^k {Z_i^2}\)被稱為服從自由度為\(k\)的卡方分佈，記作：\(X \sim {\chi ^2}\left( k \right)\)。

二.卡方概率密度函數
卡方分佈的概率密度函數為：

\[{f_x}\left( x \right) = \frac{1}{{{2^{\frac{k}{2}}}\Gamma \left( {\frac{k}{2}} \right)}}{x^{\frac{k}{2} - 1}}{e^{\frac{{ - x}}{2}}} \]

其中，\(x \ge 0\)，當\(x \le 0\)時\({f_x}\left( x \right) = 0\)，\(\Gamma\)表示Gamma函數。
不同自由度情況下的卡方分佈概率密度曲線圖：

隨著自由度\(k\)的增加，曲線逐漸趨於對稱。當自由度\(k\)趨近於無窮時，卡方分佈趨近正態分佈。

三.卡方檢驗
卡方檢驗是非引數檢驗，以卡方分佈為理論依據的假設檢驗方法，基本原理是通過樣本的頻數分佈來推斷總體是否服從某種理論分佈。卡方檢驗的原假設為：樣本所屬總體的分佈與理論分佈之間不存在顯著差異。卡方檢驗的檢驗統計量方程為：

\[{\chi ^2} = \sum\limits_{i = 1}^k {\frac{{{{\left( {{M_{oi}} - {M_{ei}}} \right)}^2}}}{{{M_{ei}}}}} \]

\(\chi ^2\)統計量在大樣本條件下逐漸服從自由度為\(k-1\)的卡方分佈，\(M_{oi}\)表示觀測頻數，\(M_{ei}\)表示理論頻數。\({\chi ^2}\)統計量越小，表示觀測頻數與理論頻數越接近。如果小於由顯著性水平和自由度確定的臨界值，那麼認為樣本所屬的總體分佈與理論分佈無顯著差異。

四.卡方檢驗例子
實驗目的：想知道不同年齡組的樣本個數是否存在顯著差異。如果\(p>0.05\)，那麼接受原假設，即不同年齡組的樣本個數並不存在顯著不同。
變數檢視如下所示：

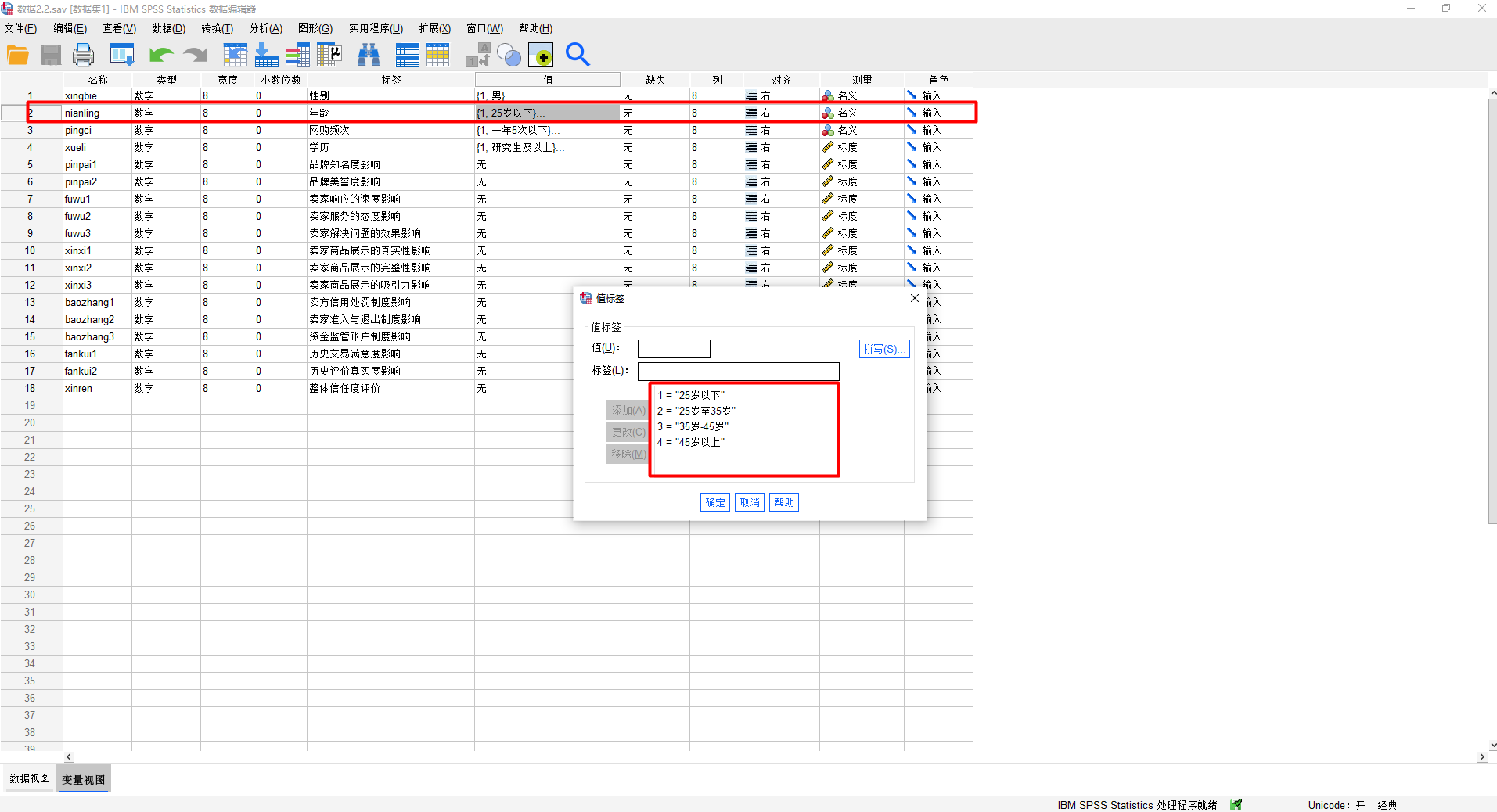
資料檢視如下所示：

分析->非引數檢驗->舊對話方塊->卡方：

卡方檢驗結果如下所示：

重點說明下卡方、自由度和漸近顯著性是如何計算的：
1.卡方計算

\[\frac{{{{\left( {45 - 50} \right)}^2}}}{{50}} + \frac{{{{\left( {51 - 50} \right)}^2}}}{{50}} + \frac{{{{\left( {52 - 50} \right)}^2}}}{{50}} + \frac{{{{\left( {52 - 50} \right)}^2}}}{{50}} = \frac{{25 + 1 + 4 + 4}}{{50}} = \frac{{34}}{{50}} = 0.68 \]

2.自由度計算
\(k-1\)，\(k\)表示分類變數數。
3.漸近顯著性計算
漸近顯著性就是\(p\)值，\(p=1-F(卡方值,自由度)\)。使用Python程式碼計算：

from scipy.stats import chi2
# 第1個參數列示卡方值，第2個參數列示自由度
p = 1 - chi2.cdf(0.68, 3)
print(p) # 0.8778977619609463

在平時看的醫學論文中，比較常見的場景是根據卡方檢驗來計算患者組和對照組的性別是否具有顯著性差異：

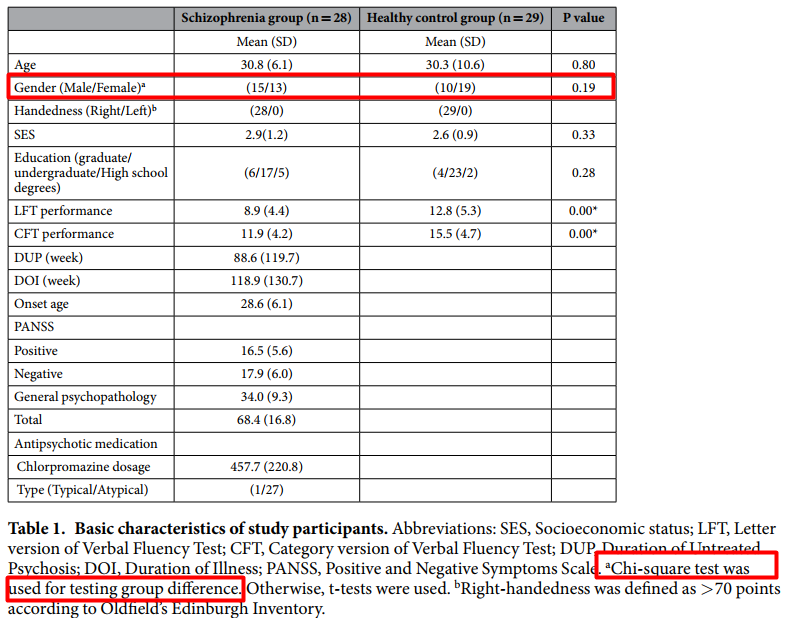
參考文獻：
[1]卡方分佈：https://zh.wikipedia.org/zh-hans/卡方分佈
[2]《SPSS統計分析入門與應用精解》
[3]卡方檢驗：https://www.ibm.com/docs/zh/spss-statistics/28.0.0?topic=tests-chi-square-test
[4]資料2.2.sav: https://url39.ctfile.com/f/2501739-875711187-f3dbb8?p=2096 (存取密碼: 2096)