從哲學角度思考虛擬的東西有必要嗎？

人類可能是唯一一個能夠構想出不存在的事物的物種，這個能力對我們來講非常重要。

說實話，虛數其實不好理解，因為這個數是之前的數學家虛構、想象出來的。那麼這種虛構的數一定是抽象的，就像我們說的負數，你就很難說它存在或者不存在，當你說「我有-1個蘋果」，那麼這個-1在現實生活中其實是毫無意義的，現實中我們看不見也摸不著的這-1個蘋果，但是你也能接受-1這個數的概念的存在，沒有覺得-1這個數位它是不存在的，或者對它的存在性質疑。

在我們生活的世界裡，還存在著大量的構想出來的東西。比如早期的人類要靠宗教崇拜團結起來，雖然最後一起去打仗，去探險的都是人，但是要沒有宗教，人和人直接溝通，達不到團結的目的（前一陣讀到一則材料也提到，原始人的團結共同作業就是需要語言發揮共同想象的能力，也就是「講故事」的能力，比如「山的那一邊有一片果樹林」等等，而現代社會的很多實體虛體其實也是人們的「共同想象」，比如國家、民族、貨幣、公司、工會等等，這就是人和動物的本質區別之一 Image）。

雖然現在的人不太需要宗教了，但是很多虛擬的概念已經深入我們人心，比如法律、有限公司、法人團體等概念便是如此，它們在自然界中並不存在，只是人們腦子裡構建出的概念，但是如果沒有它們，我們這個社會就執行不下去。當我們習慣於使用這些虛構的概念後，就會自然而然的把它們真實化，感覺和真的一樣，甚至可以達到不可或缺的程度。

今天，衡量一個人認知水平的一個方法，就是要看他接受虛擬概念的能力有多強，如果他只停留在看得見摸得著的東西，這個人的水平就不是很高。我們經常說那些只知道買房置地，收藏奢侈品的人是土財主、暴發戶，其實也是這個道理。

其次，虛數的出現，標誌著人類對數這個概念認識的進步，特別是從形象思維到抽象思維的進步。

化學中的催化劑
我們知道，催化劑在化學反應完成前後是不改變的，它只是起到一個媒介的作用，但是沒有它，化學反應要麼特別慢，要麼乾脆進行不下去。
法律學的概念——法人
我們不妨看一個法律學的概念——法人，在早期的羅馬法中，提出了法律主體的概念，它最初只涉及到自由人，後來因為要處理經濟糾紛，就把一些機構看成是法律的主體，當作人一樣看待，這就是法人概念的來源。這些法人，其實就相當於數學中所說的虛數的概念。
我們今天和一個公司打官司，其實在打官司的過程中接觸到的還是人，但是你不會去告裡面某個具體的人，而是針對這個虛構出的組織。當你打贏這個官司後，是裡面具體的人執行對你的賠償，但是你拿到的賠償卻是法人這個機構給你的。這就如同解方程時，我們需要藉助於虛數，才能得到實數的解一樣。

但是實話實說，虛數確實不是必要的：
認為虛數很「虛」很沒有「存在感」的另一原因似乎是，在生活中人們好像的確用不到虛數。比如，我們描述今天吃了幾個蘋果？今天的溫度，車子的奔跑速度...我們都用不到虛數。
而且它與我們的感官不相符，複數可以像向量一樣有方向，這就與人們印象中的數位(量)不大一樣。
所以，在某些特定的物理場合，我們使用虛數，那是因為虛數有適合的規則，儘管參照虛數很方便，但歸根到底這只是一種數學工具罷了，並且這個工具不是唯一的，可以用其它數學工具去替換這個工具。

總結：當遇到有需求的場景，just use it.

虛數就是一次新突破———虛軸（旁軸）

首先恭喜你，如果你之前不瞭解虛數和複數的話，那你現在馬上就要突破一次思維的限制，就類似剛剛在初中學習到負數時的震撼。

如果說負數是在實數軸的左邊，那虛數就是衡數軸中多了一個虛擬豎軸，

那麼從找 x^2+1=0 方程解的過程來看，發現在實數軸上找不到解，但在複平面上卻可以找到函數的解，只不過，這兩個解落在了實數軸以外。這個拓展出來的虛軸（高斯叫它旁軸），是一個新的維度，我們只能說虛數存在在了一個拓展出的維度中，一個看似抽象但是可以被我們想象到的維度中。

怎麼用圖形表示？

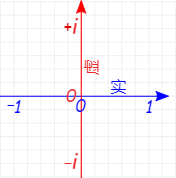
這個所謂的虛軸，確實比較考驗想象力，受自身認知的侷限性，我也是看了半天才理解（本人較為愚鈍），但是如果我們能打破自身刻板的思維，尤其是習慣用複平面思考問題後，我們可能就會對複數的實在性有一個新的認識，得到一次對自身認證的突破機會。
最後提升一下，還是在於多使用，多練，腦子就能處理得輕鬆一些。

學習建議

把焦點放在「關係」上，而不是數學公式；
將複數視為對現有數位系統的一次升級，就像曾經的 0、小數以及負數升級了當時的數位系統那樣；
通過視覺圖表而不是文字來理解概念；
虛數的使用類似求圓的面積公式，A=πr^2 , 你可以不用懂這個π是什麼，直接套入即可；
虛數有點類似python的語法糖，Java的註解，只需要在類和函數旁邊加上一個符號，就能自動增加了一個功能；

What is imaginary number？

虛數單位 i 等於負1的平方根；
虛數 = √-1 = i

通過一個二次方程解法問題，引出了虛數的概念

在實數的範圍內，X^2+1=0是無解的，這樣一來，有的多項式方程有解，有的無解，數學就不完美了。
引入一個虛擬的概念，虛數i，就讓所有的方程都變得有解了。更漂亮的是，引入虛數的概念後，所有的一元N次方程都會有N個解，沒有例外。

引入虛數的案例

Example，求-9的平方根是什麼？

Example, 解 x^2=-1 ,求x

有點繞

虛數在座標上的作用——旋轉

虛數單位 i 有個有趣的屬性————旋轉。它自乘的積在四個答案裡"迴圈重複"：

Example , 求i^6得多少？

What is complex number?

複數 = z = a+bi

複數的結構

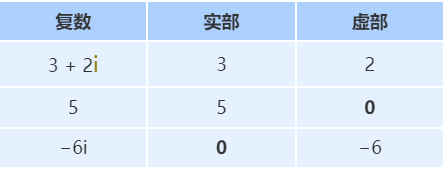
什麼是複平面?

複平面是一個由實數軸和虛數軸組成的平面，也稱為阿氏平面。在複平面上，實數軸通常被標記為水平軸，虛數軸通常被標記為垂直軸。有時也會將實數軸標記為 x 軸，將虛數軸標記為 y 軸。

視覺介紹：
複數平面是一個平面，在這平面上：
實數從左到右排列，
同時
虛數從下到上排列。

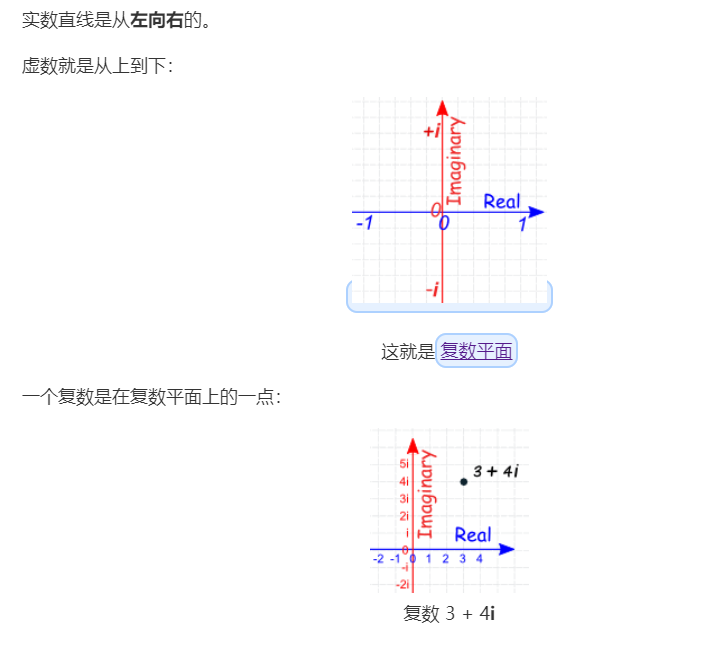
在複平面上，每個複數都可以表示為一個有序數對 (a, b)，其中 a 是實部，b 是虛部。可以將這個有序數對看作是一個向量，它的起點是原點，終點是複平面上的某個點。向量的長度表示了這個複數的模，也就是其絕對值。向量的方向表示了這個複數的幅角，也就是它與正實數軸之間的夾角。

複數的加法和減法可以通過向量的平移來表示，也就是將一個向量平移到另一個向量的位置。複數的乘法可以通過將兩個複數對應的向量首尾相接成一個平行四邊形，然後計算這個平行四邊形的對角線向量，即為兩個複數的乘積。通過複平面上向量的運算，我們可以更加直觀地理解複數的運算，並且可以方便地進行計算和推導。

Range of numbers

笛卡爾發現虛數出現後，在「直角座標系」上建立了「複平面」，用公式可表示為：z=a+bi。
在人們沒有發現複平面時，人們常常感覺「數不夠用。現在，數學家們現己經嚴格證明，「一切數」都能在複平面中找到，「數的範圍」不會再超過複數的範圍。

複數就是向量

可以做運算，

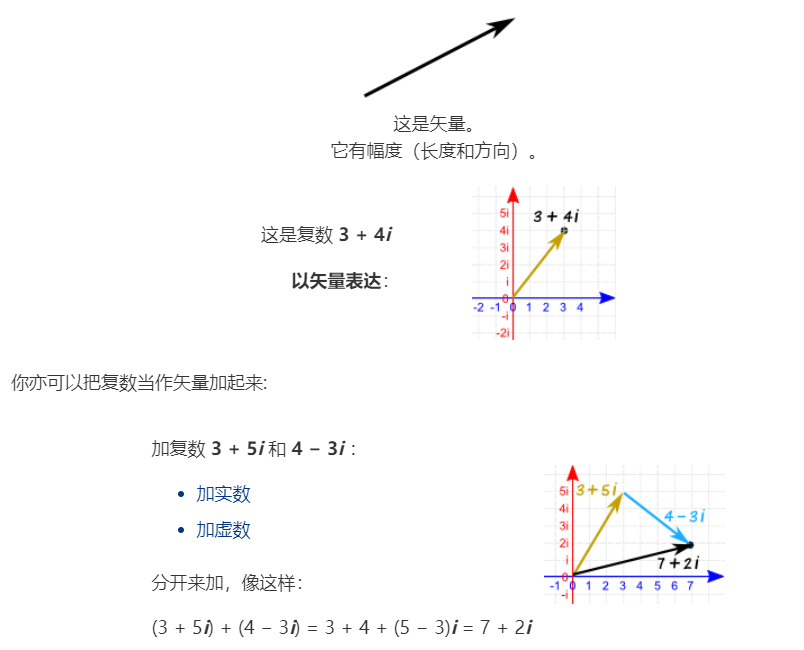
為了避免篇幅過長，這裡不詳細講加減、乘除運算，
用到再去查公式就行了，就是需要注意：乘法和除法涉及到共軛概念。

求極型（極座標）

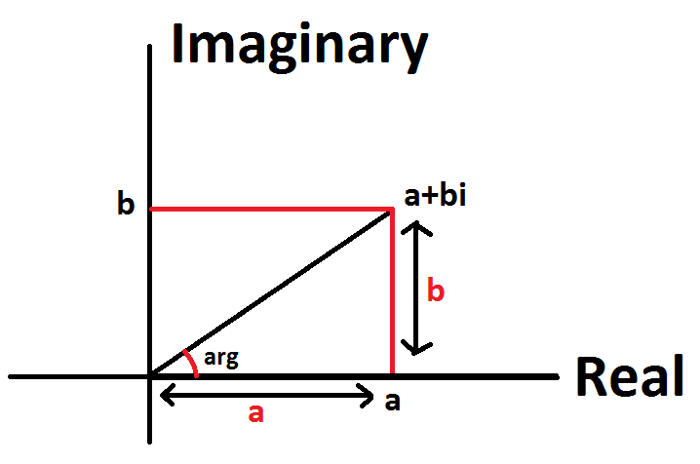
笛卡兒座標到極座標轉換可以互相轉換：

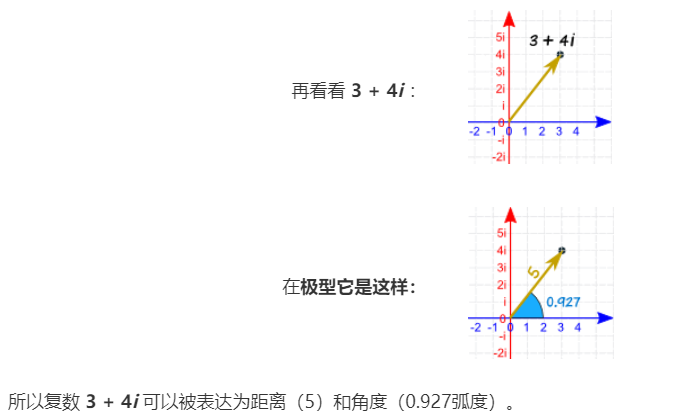
具體公式，我這邊不在描述，有需要的同學，問下GPT、查資料。

Application scenarios

人過普通生活時，負數也沒什麼用，但是負數在理論分析、資料統計中依然非常有用，這是顯然的。因此，數域的擴充套件，不是讓它在買菜時有用，而是為了讓邏輯更嚴密、讓理論分析更方便。

波、週期
虛數在交流電路分析中，就非常有用，虛數可以表示幅度和旋轉角，這正是正弦波的重要引數。
極座標與應用
虛數作為數學工具最大的用途，可能是便於將直角座標變成極座標。
簡單地講，在飛行、航海等場景裡，極座標更方便使用，比如我們說往兩點鐘的方向飛行 20 公里，這就是極座標的描述方式。在極座標的計算中，如果只用實數，非常複雜，如果引入虛數，就極為簡單。
虛數是解一元三次方程的必須工具；

Reference

https://www.shuxuele.com/numbers/imaginary-numbers.html
https://www.shuxuele.com/numbers/complex-numbers.html
https://www.shuxuele.com/algebra/complex-plane.html

學習抽象概念案例，虛數和複數