淺談線段樹
線段樹
引入
線段樹是較為常用的資料結構,一般用於維護區間資訊。
線段樹可以在 \(O(\log n)\) 的時間複雜度內實現單點修改,區間修改,區間查詢等操作。
一般的在區間上進行操作的題目都可以考慮線段樹。
普通線段樹
基本思想
線段樹,顧名思義,就是由線段組成的樹。
我們結合圖來理解一下:
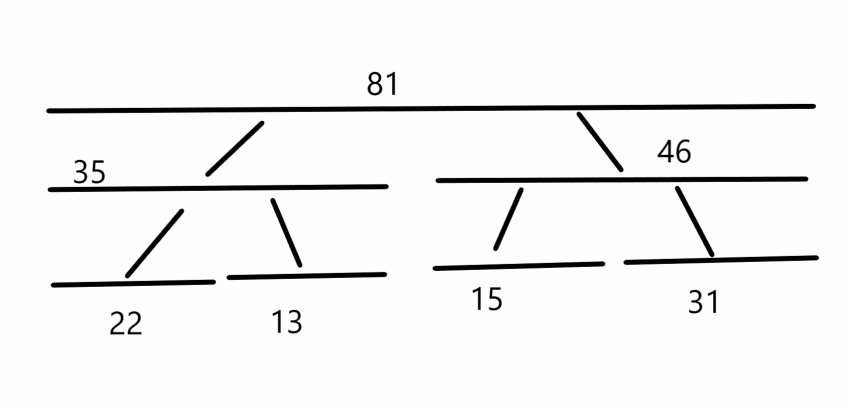
最下方的是葉子結點,存放著原來數列的值,從上往下,可以看作是把整個序列的總和看作一條長線段,然後掰開放下去,一直掰倒不能再掰為止,也就是到了葉子節點。
所有點維護的都是當前端點的區間內的資訊,比如上圖是總和,而葉子結點比較特殊,是左右端點相等的區間。
這麼好用的東西該怎麼用呢?
修改操作的靈魂——lazy tag
我們從名字可以看出他是讓我們偷懶用的。
我們在每一個結點都有一個對應的 lazytag ,他的具體作用就是存放當前的修改操作的值,比如說我區間加了一個值,如果要是當前結點代表的區間屬於要修改的區間的話,我先存到這個裡面,我先不下傳,我只改這一個,這個時候我們的修改操作就大幅度加快了,在我們進行查詢類的操作的時候,用到這個點的資訊了,我們再下傳給兩個兒子結點,但也只是僅下傳給兩個兒子結點,因為可能兒子節點的資訊是用不到的,所以我們還是秉持「能省就省」的原則,不去繼續下傳。
當然一個 lazytag 只能用於一個操作,比如讓你同時進行區間加區間乘的話,還是老老實實開兩個 lazytag 比較好。
變數與宏定義
#define int long long
#define N 1000100
#define rs x<<1|1
#define ls x<<1
using namespace std;
int n, m, a[N];
struct sb {int l, r, len, tag, sum;} e[N];
這個其實不是很重要,主要看個人喜好,這裡為了防止對後面的程式碼理解出現問題才放上來,裡面的 ls 是左兒子結點編號,rs 是右兒子結點編號。
結構體裡面的 tag 就是 lazytag 後面會講到,len 是當前區間的長度,l,r 是當前結點代表區間的左右端點,sum 代表的就是當前區間內的總和。
更新函數
這個按理來說是沒有必要寫個函數的,但是我喜歡寫成函數。
inline void push_up(int x) { e[x].sum = e[ls].sum + e[rs].sum; }
inline void push_down(int x)
{
if(! e[x].tag) return ;
e[ls].tag += e[x].tag;
e[rs].tag += e[x].tag;
e[ls].sum += e[ls].len * e[x].tag;
e[rs].sum += e[rs].len * e[x].tag;
e[x].tag = 0;
return ;
}
這裡的 push_up 函數就是用來更新當前點的 sum 值的,我們幾乎在進行完所有操作都要呼叫一次,而在呼叫的時候,基本上都是進行完有關修改的操作的時候才進行。
push_down 函數是用來下傳 lazytag 的,正如前文所說的,我們只下傳到左右兩個兒子即可,首先就是把當前點的 lazytag 的值給加到左右兒子的 lazytag 上,因為之前的左右兒子可能有沒下傳的 lazytag ;然後就是修改左右兒子的 sum ,具體就用到我們之前的 len 了,我們都知道累加的時候是整個區間每一個數都加,所以 sum 加的就是區間長度 \(\times\) 加上的值,最重要的一點就是我們要把當前下傳完的點的 lazytag 給清空。
建樹
我們上面打過一個比方,就是把一個序列給掰開,然後放下,再掰,一直到不能掰了為止。
這裡我們是把大區間給不斷從中間分開,一直分到不能再分,也就是到了葉子節點,也就是 \(l = r\) 的時候。
具體我們通過以下的程式碼來進行實現。
inline void build(int x, int l, int r)
{
e[x].l = l;
e[x].r = r;
e[x].len = r - l + 1;
if(l == r)return e[x].sum = a[l], void();
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
push_up(x);
return ;
}
其中的 push_up 函數就是利用更新完的子節點的總和更新當前節點的區間內的數的總和。
然後通過 build 函數我們得到了一棵樹。
注意在這裡我們可以直接把 l,r,sum 給處理出來,然後如果當前點代表的區間左右端點相等,說明當前點就是葉子節點,我們把對應的原序列的值賦給他。
區間求和
我們在求和的時候如果要是暴力的話肯定不行,考慮我們維護的 sum 有什麼作用。
每一個結點的 sum 表示當前點代表的區間的所有數的總和,所以我們在查詢的時候,也跟建樹一樣一半一半的往下傳,如果傳到一個點,他代表的區間屬於當前我們要查的區間,我們就不必下傳到葉子結點,直接返回當前點的 sum 即可。
inline int ask(int x, int nl, int nr)
{
if(nl <= e[x].l && nr >= e[x].r) return e[x].sum;
push_down(x);
int res = 0, mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) res += ask(ls, nl, nr);
if(nr > mid) res += ask(rs, nl, nr);
return res;
}
nl,nr 為要查詢的區間的左右端點。
需要注意一點是,我們在每一次進行往下傳的時候,我們需要先下傳一下當前點的 lazytag 來保證左右兒子的值是修改完的。
對於當前要查詢的區間的左端點小於等於 mid 就繼續往下查詢左兒子;當前要查詢的區間的右端點大於 mid 的時候就繼續往下查詢右兒子。
區間修改
我們在修改的時候需要用到和區間求和一樣的思想。
inline void add(int x, int nl, int nr, int v)
{
if(nl <= e[x].l && nr >= e[x].r)
{
e[x].tag += v;
e[x].sum += e[x].len * v;
return ;
}
push_down(x);
int mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) add(ls, nl, nr, v);
if(nr > mid) add(rs, nl, nr, v);
push_up(x);
return ;
}
先 push_down 一下是因為後面修改完是要 push_up 的,這樣我們必須下傳一下 lazytag 才能保證更新完以後的值是正確的。
我們在這裡更新主要還是為了上面的查詢操作。
到這裡你就可以通過這道題目了:【模板】線段樹 1 - 洛谷
完整 code:
#include <bits/stdc++.h>
#define int long long
#define N 1000100
#define rs x<<1|1
#define ls x<<1
using namespace std;
int n, m, a[N];
struct sb {int l, r, len, tag, sum;} e[N];
inline void push_up(int x) { e[x].sum = e[ls].sum + e[rs].sum; }
inline void push_down(int x)
{
if(! e[x].tag) return ;
e[ls].tag += e[x].tag;
e[rs].tag += e[x].tag;
e[ls].sum += e[ls].len * e[x].tag;
e[rs].sum += e[rs].len * e[x].tag;
e[x].tag = 0;
return ;
}
inline void build(int x, int l, int r)
{
e[x].l = l;
e[x].r = r;
e[x].len = r - l + 1;
if(l == r)return e[x].sum = a[l], void();
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
push_up(x);
return ;
}
inline void add(int x, int nl, int nr, int v)
{
if(nl <= e[x].l && nr >= e[x].r)
{
e[x].tag += v;
e[x].sum += e[x].len * v;
return ;
}
push_down(x);
int mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) add(ls, nl, nr, v);
if(nr > mid) add(rs, nl, nr, v);
push_up(x);
return ;
}
inline int ask(int x, int nl, int nr)
{
if(nl <= e[x].l && nr >= e[x].r) return e[x].sum;
push_down(x);
int res = 0, mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) res += ask(ls, nl, nr);
if(nr > mid) res += ask(rs, nl, nr);
return res;
}
signed main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> a[i];
build(1, 1, n);
for(int i = 1; i <= m; i ++)
{
int op, x, y, z;
cin >> op;
if(op == 1)
{
cin >> x >> y >> z;
add(1, x, y, z);
}
if(op == 2)
{
cin >> x >> y;
cout << ask(1, x, y) << endl;
}
}
return 0;
}
區間乘 && 區間加
不能說是難,只能說很麻煩。
我們在之前提到過如果有多個操作的話一個 lazytag 是不夠用的,所以我們需要多開一個來分別存放加和乘的 lazytag 。
我這裡是用 tag1 來表示區間加的 lazytag ,用 tag2 來表示區間乘的 lazytag 。
我們需要更改的就是之前的 push_down 函數,因為我們相較上一個題目,只是多開了一個 lazytag ,所以我們這樣寫:
inline void push_down(int x)
{
if(e[x].tag1 == 0 && e[x].tag2 == 1) return ;
e[ls].tag2 = (e[ls].tag2 * e[x].tag2) % P;
e[rs].tag2 = (e[rs].tag2 * e[x].tag2) % P;
e[ls].tag1 = (e[ls].tag1 * e[x].tag2 + e[x].tag1) % P;
e[rs].tag1 = (e[rs].tag1 * e[x].tag2 + e[x].tag1) % P;
e[ls].sum = (e[ls].sum * e[x].tag2 % P + e[ls].len * e[x].tag1) % P;
e[rs].sum = (e[rs].sum * e[x].tag2 % P + e[rs].len * e[x].tag1) % P;
e[x].tag1 = 0;
e[x].tag2 = 1;
return ;
}
我們和之前的 push_down 函數的區別就是當前的多考慮了一個乘的 lazytag ,其實也就是多修改了一個 lazytag ,乘的就是直接乘上,但是對於加的 lazytag 需要先乘一下當前下傳的點的 tag2 然後再加上 tag1 ,這是因為如果要是當前點的 tag2 肯定是在兒子結點的 tag1 的後面的,因為我們在處理的時候遇到乘會直接先把 tag1 給乘上,這樣我們就必須先讓兒子結點的 tag1 給乘上當前結點的 tag2 ,然後再加上當前結點的 tag1 就可以保證值是不變的。
再來看區間乘的操作函數:
inline void add2(int x, int nl, int nr, int v)
{
if(nl <= e[x].l && nr >= e[x].r)
{
e[x].tag1 = (e[x].tag1 * v) % P;
e[x].tag2 = (e[x].tag2 * v) % P;
e[x].sum = (e[x].sum * v) % P;
return ;
}
push_down(x);
int mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) add2(ls, nl, nr, v);
if(nr > mid) add2(rs, nl, nr, v);
push_up(x);
return ;
}
和區間加的操作函數的區別就是遇到噹噹前點代表的區間是屬於要修改的區間的時候,我們就需要先把當前點的 tag1 給乘上要乘的數,因為很明顯當前的乘的操作是在 tag1 的後面,所以裡面的值也要乘上要乘的數,然後再對 tag2 進行修改,也就是直接乘上即可。
完整 code:
#include <bits/stdc++.h>
#define int long long
#define N 100100
#define rs x << 1 | 1
#define ls x << 1
using namespace std;
int n, m, a[N], P;
struct sb { int l, r, len, tag1, tag2 = 1, sum; } e[N << 2];
inline void push_up(int x) { e[x].sum = (e[ls].sum + e[rs].sum) % P; }
inline void push_down(int x)
{
if(e[x].tag1 == 0 && e[x].tag2 == 1) return ;
e[ls].tag2 = (e[ls].tag2 * e[x].tag2) % P;
e[rs].tag2 = (e[rs].tag2 * e[x].tag2) % P;
e[ls].tag1 = (e[ls].tag1 * e[x].tag2 + e[x].tag1) % P;
e[rs].tag1 = (e[rs].tag1 * e[x].tag2 + e[x].tag1) % P;
e[ls].sum = (e[ls].sum * e[x].tag2 % P + e[ls].len * e[x].tag1) % P;
e[rs].sum = (e[rs].sum * e[x].tag2 % P + e[rs].len * e[x].tag1) % P;
e[x].tag1 = 0;
e[x].tag2 = 1;
return ;
}
inline void build(int x, int l, int r)
{
e[x].l = l;
e[x].r = r;
e[x].len = r - l + 1;
if(l == r) return e[x].sum = a[l], void();
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
push_up(x);
return ;
}
inline void add1(int x, int nl, int nr, int v)
{
if(nl <= e[x].l && nr >= e[x].r)
{
e[x].tag1 = (e[x].tag1 + v) % P;
e[x].sum = (e[x].sum + e[x].len * v) % P;
return ;
}
push_down(x);
int mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) add1(ls, nl, nr, v);
if(nr > mid) add1(rs, nl, nr, v);
push_up(x);
return ;
}
inline void add2(int x, int nl, int nr, int v)
{
if(nl <= e[x].l && nr >= e[x].r)
{
e[x].tag1 = (e[x].tag1 * v) % P;
e[x].tag2 = (e[x].tag2 * v) % P;
e[x].sum = (e[x].sum * v) % P;
return ;
}
push_down(x);
int mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) add2(ls, nl, nr, v);
if(nr > mid) add2(rs, nl, nr, v);
push_up(x);
return ;
}
inline int ask(int x, int nl, int nr)
{
if(nl <= e[x].l && nr >= e[x].r) return e[x].sum;
push_down(x);
int res = 0, mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) res = (res + ask(ls, nl, nr) ) % P;
if(nr > mid) res = (res + ask(rs, nl, nr) ) % P;
return res % P;
}
signed main()
{
cin >> n >> m >> P;
for(int i = 1; i <= n; i ++) cin >> a[i];
build(1, 1, n);
for(int i = 1; i <= m; i ++)
{
int op, x, y, z;
cin >> op;
if(op == 1)
{
cin >> x >> y >> z;
add2(1, x, y, z);
}
if(op == 2)
{
cin >> x >> y >> z;
add1(1, x, y, z);
}
if(op == 3)
{
cin >> x >> y;
cout << ask(1, x, y) << endl;
}
}
return 0;
}
區間 max/min
沒找到帶修改操作的題目,或許是因為太毒瘤而且我也不會寫。
我們建一下樹,在建樹的過程中只要把之前求和的 push_up 改成求 min 即可。
然後對於詢問操作,我們就直接和之前的區間加一樣,但是區別就是我們把累加改成求 min。
code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define int long long
#define N 1001000
#define rs x << 1 | 1
#define ls x << 1
using namespace std;
int n, m, a[N];
struct sb { int l, r, maxn; } e[N];
inline void push_up(int x) { e[x].maxn = min(e[ls].maxn, e[rs].maxn); }
inline void build(int x, int l, int r)
{
e[x].l = l;
e[x].r = r;
if(l == r) return e[x].maxn = a[l], void();
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
push_up(x);
return ;
}
inline int ask(int x, int nl, int nr)
{
if(nl <= e[x].l && nr >= e[x].r) return e[x].maxn;
int res = INF, mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) res = min(res, ask(ls, nl, nr) );
if(nr > mid) res = min(res, ask(rs, nl, nr) );
return res;
}
signed main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> a[i];
build(1, 1, n);
for(int i = 1; i <= m; i ++)
{
int l, r;
cin >> l >> r;
cout << ask(1, l, r) << " ";
}
return 0;
}
區間覆蓋 && 區間加
單純的區間覆蓋沒找到,所以用這道。
其實和區間乘 && 區間加的那道題目差不多。
用 tag1 表示區間加的 lazytag ,用 tag2 表示區間覆蓋的 lazytag 。
我們在進行覆蓋的修改函數的時候,我們就直接把當前點的 tag1 給清空成 \(0\) 即可,因為都被覆蓋了,在那之前的操作也無意義了。
然後我們在處理的時候也是和區間乘一樣先處理區間覆蓋的 lazytag 然後再進行區間加的 lazytag 的修改。
code:
#include <bits/stdc++.h>
#define INF LONG_LONG_MAX
#define int long long
#define N 1000100
#define rs x << 1 | 1
#define ls x << 1
using namespace std;
int n, m, a[N];
struct sb {int l, r, len, sum, tag1, tag2 = -INF;} e[N << 2];
inline int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){f=ch!='-';ch=getchar();}while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return f?x:-x;}
inline void push_up(int x) { e[x].sum = max(e[ls].sum, e[rs].sum); }
inline void push_down(int x)
{
if(e[x].tag2 != -INF)
{
e[ls].tag1 = 0;
e[rs].tag1 = 0;
e[ls].sum = e[ls].tag2 = e[x].tag2;
e[rs].sum = e[rs].tag2 = e[x].tag2;
e[x].tag2 = -INF;
}
if(e[x].tag1)
{
e[ls].tag1 += e[x].tag1;
e[rs].tag1 += e[x].tag1;
e[ls].sum += e[x].tag1;
e[rs].sum += e[x].tag1;
e[x].tag1 = 0;
}
return ;
}
inline void build(int x, int l, int r)
{
e[x].l = l;
e[x].r = r;
e[x].len = r - l + 1;
if(l == r) return e[x].sum = a[l], void();
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
push_up(x);
return ;
}
inline void add(int x, int nl, int nr, int v)
{
if(nl <= e[x].l && nr >= e[x].r)
{
e[x].tag1 += v;
e[x].sum += v;
return ;
}
push_down(x);
int mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) add(ls, nl, nr, v);
if(nr > mid) add(rs, nl, nr, v);
push_up(x);
return ;
}
inline void cover(int x, int nl, int nr, int v)
{
if(nl <= e[x].l && nr >= e[x].r)
{
e[x].tag1 = 0;
e[x].sum = e[x].tag2 = v;
return ;
}
push_down(x);
int mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) cover(ls, nl, nr, v);
if(nr > mid) cover(rs, nl, nr, v);
push_up(x);
return ;
}
inline int ask(int x, int nl, int nr)
{
if(nl <= e[x].l && nr >= e[x].r) return e[x].sum;
push_down(x);
int res = -INF, mid = (e[x].l + e[x].r) >> 1;
if(nl <= mid) res = max(res, ask(ls, nl, nr) );
if(nr > mid) res = max(res, ask(rs, nl, nr) );
return res;
}
signed main()
{
n = read();
m = read();
for(int i = 1; i <= n; i ++) a[i] = read();
build(1, 1, n);
for(int i = 1; i <= m; i ++)
{
int op = read(), l, r, x;
if(op == 1)
{
l = read(), r = read(), x = read();
cover(1, l, r, x);
}
if(op == 2)
{
l = read(), r = read(), x = read();
add(1, l, r, x);
}
if(op == 3)
{
l = read(), r = read();
cout << ask(1, l, r) << endl;
}
}
return 0;
}
其他操作
其他的操作比如區間開平方,區間次冪啥的都是噁心人的東西其實是我不會,當然線段樹的題目都是將題目所需要的資訊給維護一下,讓時間複雜度更優。
到這裡普通的線段樹就告一段落了。
拓展——權值線段樹
這個東西算是主席樹的弱化版,不支援詢問歷史版本。
我們都知道桶排序,開一個陣列記錄和其下標相等的值的出現次數,權值線段樹的思想也是這樣。
比較經典的應用就是求逆序對。
我們考慮將資料排序並離散化後維護每一個數出現的次數。
我們在遍歷到一個數的時候,先用 lower_bound 來查詢位置,然後用 ask 函數來查詢當前比他小的數出現了多少個,然後我們用 i-1-cnt (cnt 為當前比他小的數的個數)來計算當前在序列裡在當前數的前面但是比他大的數的個數,然後加到答案裡,然後再把當前數插入即可。
code:
#include <bits/stdc++.h>
#define int long long
#define N 1000100
#define rs (x << 1 | 1)
#define ls (x << 1)
using namespace std;
int n, m, a[N], v[N], ans;
struct sb {int l, r, sum;} e[N << 2];
inline void push_up(int x) { e[x].sum = e[ls].sum + e[rs].sum; }
inline void build(int x, int l, int r)
{
e[x].l = l;
e[x].r = r;
if(l == r) return ;
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
return ;
}
inline void add(int x, int k)
{
if(e[x].l == e[x].r) { e[x].sum ++; return ; }
int mid = (e[x].l + e[x].r) >> 1;
if(k <= mid) add(ls, k);
else add(rs, k);
push_up(x);
return ;
}
inline int ask(int x, int nl, int nr)
{
// cout<<x<<endl;
if(nl <= e[x].l && nr >= e[x].r) return e[x].sum;
int mid = (e[x].l + e[x].r) >> 1, res = 0;
if(nl <= mid) res += ask(ls, nl, nr);
if(nr > mid) res += ask(rs, nl, nr);
return res;
}
signed main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> a[i], v[i] = a[i];
sort(v + 1, v + n + 1);
m = unique(v + 1, v + n + 1) - v - 1;
build(1, 1, n);
for(int i = 1; i <= n; i ++)
{
int k = lower_bound(v + 1, v + m + 1, a[i]) - v;
int cnt = ask(1, 1, k);
// cout << "k:" << k <<endl;
// cout << "cnt:" << cnt << endl;
ans += (i - 1 - cnt);
add(1, k);
}
cout << ans << endl;
return 0;
}
優化空間——動態開點
我們通常的線段樹開的空間是資料要求的四倍,這樣才能保證不會出現不夠用的情況,但是有的時候會爆空間,但是我們如果開小一兩倍是不會爆的。
這個時候我們有可能開四倍有一堆是沒用的,那麼我們開這麼多會顯得很傻,這個時候就需要我們接下來要講的動態開點線段樹。
動態開點的意思就是我們不像前面說的一樣嘎嘎開上四倍,然後一個 build 函數遞迴到底,而是當我們不需要這個點的時候,我們就先不開,等我們需要用了,我們直接新建一個點,這樣就可以解決空間問題了。
但是有一個缺點就是左右兒子的編號不像之前那樣有規律可以用 x<<1,x<<1|1 來表示,這個時候我們就可以用兩個陣列標記一下。
我們考慮一下如何用線段樹來求這個方案數。
首先看到 \(10^{9}\) 的資料範圍,就知道普通的線段樹是會 MLE 的,所以我們用上剛剛新學的東西——動態開點線段樹。
我們讀到題目就知道是求符合要求的一段連續的子區間,所以我們可以直接先預處理出來字首和,然後我們考慮從 \(x\sim i\) 的合法方案應該去哪裡找
分開解一下就是:
那麼我們想到之前的權值線段樹,我們對於每一個字首和都開一個點來維護個數,然後我們遍歷到一個點先找大於等於 \(sum_{i} - R\) 且小於等於 \(sum_{i}-L\) 的點的個數,注意不能全插完再找,因為必須是連續的子序列,所以我們當前點只能和前面的字首和組合。我們查詢完以後就直接插入即可。
code:
#include <bits/stdc++.h>
#define int long long
#define N 1010000
using namespace std;
const int M = 1e10;
struct sb {int ls, rs, sum;} e[N * 6];
int n, rt, tot = 0, L, R, sum[N], ans;
inline int node()//動態開點
{
tot++;
e[tot].ls = e[tot].rs = e[tot].sum = 0;
return tot;
}
inline void push_up(int x) { e[x].sum = e[e[x].ls].sum + e[e[x].rs].sum; }
inline void add(int x, int k, int v, int l, int r)
{
if(l == r) return e[x].sum += v, void();
int mid = (l + r) >> 1;
if(k <= mid)
{
if(! e[x].ls) e[x].ls = node();
add(e[x].ls, k, v, l, mid);
}
else
{
if(! e[x].rs) e[x].rs = node();
add(e[x].rs, k ,v, mid + 1, r);
}
push_up(x);
return ;
}
inline int ask(int x, int nl, int nr, int l, int r)
{
if(nl <= l && nr >= r) return e[x].sum;
int mid = (l + r) >> 1, res = 0;
if(nl <= mid)
{
if(! e[x].ls) e[x].ls = node();
res += ask(e[x].ls, nl, nr, l, mid);
}
if(nr > mid)
{
if(! e[x].rs) e[x].rs = node();
res += ask(e[x].rs, nl, nr, mid + 1, r);
}
return res;
}
signed main()
{
cin >> n >> L >> R;//不能超出的左右區間
for(int i = 1; i <= n; i ++)
{
int x;
cin >> x;
sum[i] = sum[i - 1] + x;//處理字首和
}
rt = node();
add(rt, sum[0], 1, -M, M);//先把樹根給插入進去,在0的位置加一
for(int i = 1; i <= n; i ++)//遍歷後面n個數
{
ans += ask(rt, sum[i] - R, sum[i] - L, -M, M);//累加答案
add(rt, sum[i], 1, -M, M);//算完就給插入進去
}
cout << ans << endl;
return 0;
}
拓展——標記永久化
此部分由 yi_fan0305 友情贊助!
我們在進行操作的時候需要下傳 lazytag ,沒有效率,所以有個聰明人又發明了可以小小優化一下常數的標記永久化。
好處:
- 碼量小,不用寫
push_down和push_up(其實我覺得比原來大了(?)。 - 在可持久化線段樹上應用該技巧能做到區間修改的效果。
壞處:
- 適用範圍有限,只有當求的東西滿足區間貢獻獨立。比如區間加法。
區間最大值就無法標記永久化。 - 多標記好像也不適用。
當然我們一般是不用的因為侷限性有些大。
我們在講 lazytag 向下遞迴的過程中,如果當前區間正好等於查詢區間,那就直接改 lazytag 和數值,倘若當前區間包含查詢區間但不與查詢區間相等,那我們只修改值,這些操作與線段樹修改操作很像。
需要注意的是,如果查詢的區間橫跨左右兩個孩子區間,那我們需要將查詢區間也從 mid 處分開。
按照一般的寫法,在向下遞迴時,我們還要用遞迴把 lazytag 也一起向下傳遞,而標記永久化則是捨棄了向下傳遞 lazytag 這個操作,我們在查詢時設定一個值,用它來記錄沿路的 lazytag ,最後一起統計即可。
為什麼要記錄沿路的 lazytag 呢?
如果包含該區間的大區間被打上了 lazytag,則說明這一整個大區間都受到這個 lazytag 的影響,所以把它記錄下來。
最後處理答案時,就是將 lazytag 的和乘上這個區間的長度,add 記錄的是 lazytag 和,可以將這個 add 看作是對於這個區間的每個元素一共要增加的值。
code:
#include <bits/stdc++.h>
#define int long long
#define N 1000100
#define rs (x << 1 | 1)
#define ls (x << 1)
using namespace std;
int n, m, a[N];
struct sb {int l, r, len, sum, tag;} e[N << 2];
inline void build(int x, int l, int r)
{
e[x].l = l;
e[x].r = r;
e[x].len = r - l + 1;
if(l == r) return e[x].sum = a[l], void();
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
e[x].sum = e[ls].sum + e[rs].sum;
return ;
}
inline void add(int x, int nl, int nr, int v)
{
e[x].sum += (nr - nl + 1) * v;
if(e[x].l == nl && e[x].r == nr) return e[x].tag += v, void();
int mid = (e[x].l + e[x].r) >> 1;
if(nr <= mid) add(ls, nl, nr, v);
else if(nl > mid) add(rs, nl, nr, v);
else add(ls, nl, mid, v), add(rs, mid + 1, nr, v);
return ;
}
inline int ask(int x, int nl, int nr, int cnt)
{
if(nl == e[x].l && nr == e[x].r) return e[x].sum + e[x].len * cnt;
int res = 0, mid = (e[x].l + e[x].r) >> 1;
if(nr <= mid) res = ask(ls, nl, nr, cnt + e[x].tag);
else if(nl > mid) res = ask(rs, nl, nr, cnt + e[x].tag);
else res = ask(ls, nl, mid, cnt + e[x].tag) + ask(rs, mid + 1, nr, cnt + e[x].tag);
return res;
}
signed main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> a[i];
build(1, 1, n);
for(int i = 1; i <= m; i ++)
{
int op, l, r, v;
cin >> op;
if(op == 1)
{
cin >> l >> r >> v;
add(1, l, r, v);
}
if(op == 2)
{
cin >> l >> r;
cout << ask(1, l, r, 0) << endl;
}
}
return 0;
}
值得一提的是,在我兩者都使用 cin cout 的時候效率並沒有差多少。
寫在最後
其實還有線段樹合併啥的沒整理但是好像線上段樹的基礎上改的越來越多了,所以這裡沒有寫,以後可能會單獨開部落格寫。
本來還打算寫一下 zkw 線段樹,看了一會兒沒看懂先鴿了。
有沒看懂的歡迎留言。