技術文章 » 實時光線追蹤（3）Ray Casting

實時光線追蹤（3）Ray Casting

2023-06-19 18:01:21

目錄

實時光追（Real-time Ray Tracing）往往是綜合了 sampling、ray casting、denoising 等各方面的方案，本文主要記錄的是 ray casting 這部分，但是術語可能更多仍然稱為 ray tracing。

硬體光追（Hardware Ray Tracing）

ray tracing 最經典的實現莫過於 ray traversal：投射一條 ray 然後遍歷所有 triangles 去做 ray-triangle 相交測試，並得到對應的 hit point。但是場景中的 triangles 數量往往數量龐大，ray traversal 也變得非常耗時，而後為了加速相交測試，便引入了加速結構（BVH，八叉樹，k-d樹等），來剪枝掉一些不可能發生相交的 triangles；但即便如此，軟體實現 ray traversal 仍然是件耗時的事。

再後來，Nvidia 推出了 RTX 系列顯示卡，開始提供硬體單元來大大加速 ray traversal 這一過程，使得 real-time ray tracing 成為了可能。從此之後，GPU 廠商都逐漸開始普及硬體光追的支援。

加速結構（Acceleration Structure，AS）

硬體光追提供了兩大層級的 AS，我們可以對這兩大層級（BLAS 和 TLAS）進行設定，但不用關心 AS 具體採用哪種空間加速結構或者具體實現。

  • BLAS（Bottom Level Acceleration Structure）：底層加速結構，一個 BLAS 對應一個 instance，其葉結點為一個 primitive（一般就是一個 triangle，如果使用自定義圖元則就是一個把該圖元包起來的 AABB box）。
  • TLAS（Top Level Acceleration Structure）：頂層加速結構，一個 TLAS 對應一個場景，其葉結點為一個 instance。

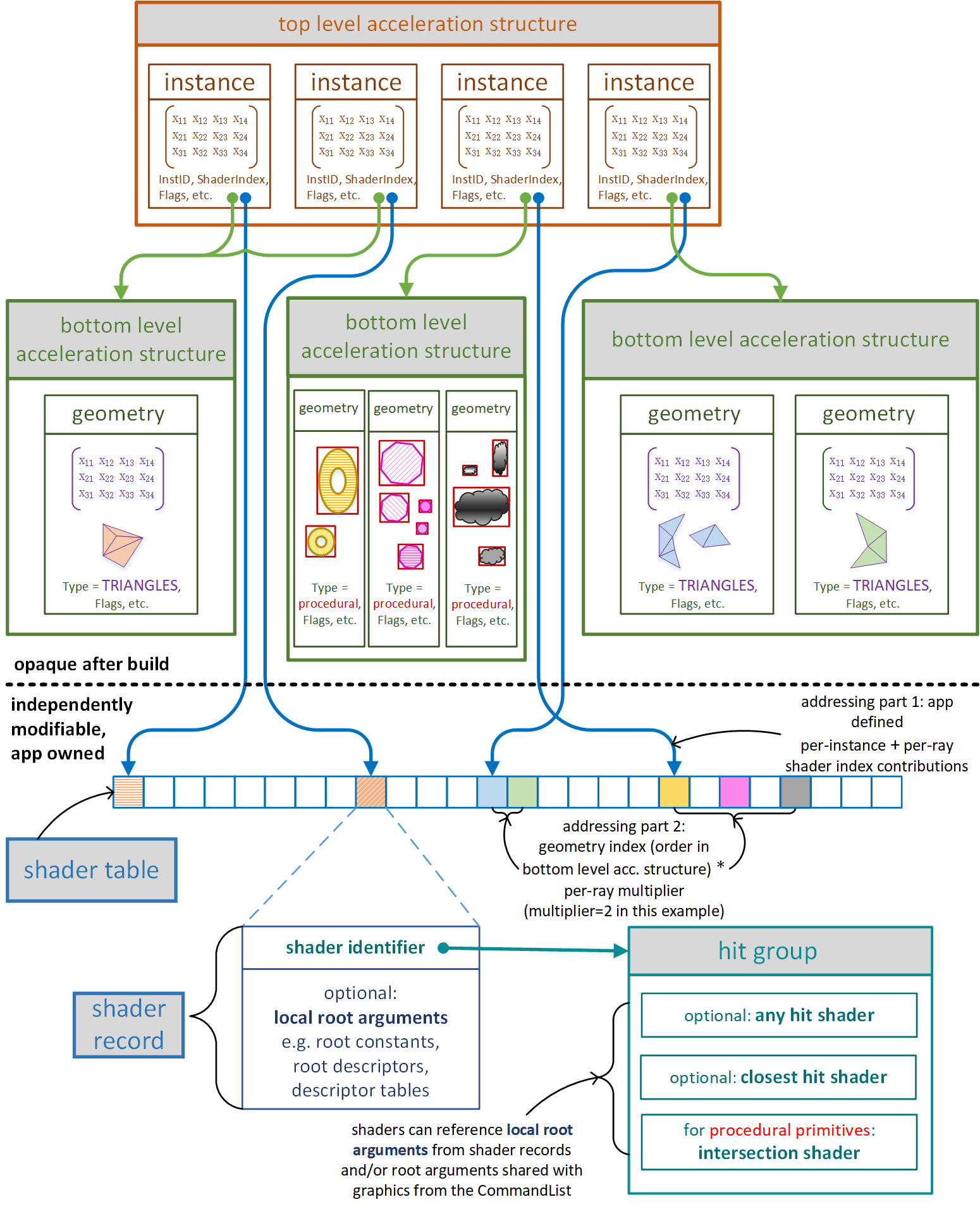
注：我們在 GPU 裡通過 ray traversal 得到 hit point 後，要獲取 hit point 的材質屬性是非常困難的，因為材質函數和引數等都是在 CPU 端的，而粗暴的直接根據 geometry id 和 material id 去 CPU 拉取對應的 shader 和引數無疑是不可行的（通訊時間過長）。

為了解決這個問題，才有了 shader table 的機制：GPU 裡的 shader table 預先儲存著一堆 shader records，每個 record 包含一個或多個 shaders（其實就是 hit group）以及引數；再得到 hit point 後，根據 geometry id 和 material id 去索引到相對應的 shader record，並直接執行對應的 shader，無需通知 CPU。

AS 策略

  • 儘可能將相同性質的多個 mesh 合併到一個 BLAS 中，而不是一個 mesh instance 一個 BLAS，這樣可以減少 BLAS 的數量，從而降低 TLAS 包含的 instances 數量。例如：由多個 mesh 組合的物件（往往需要同時rebuild或者update），可以將這多個 mesh 塞進一個 BLAS 裡；所有靜態 mesh 都塞進一個 BLAS 裡.....
  • TLAS 的質量遠比 BLAS 要重要：因為所有 ray traversal 都會經過 TLAS 先。因此對於 TLAS，我們更傾向於 rebuild 而不是 update；對於 BLAS，我們更傾向於 update 和壓縮 BLAS。
  • 儘可能減少執行時的 build/update AS 次數：物體有發生變化時，才去觸發 build AS/update AS；對 skinned meshes，可以考慮預先構建多個高質量的 AS，在不同的關鍵姿勢採用不同的 AS，而不是採用一個每幀更新的 AS。
PREFER_ FAST_ TRACE PREFER_ FAST_ BUILD ALLOW_ UPDATE Properties Example
1 no yes no 儘可能快速的 build AS，trace 效能會低於 #3 和 #4。 完全動態的幾何物體，如粒子、破壞物、移動劇烈的物體（爆炸）等，這種往往都需要每幀重建 AS。
2 no yes yes build AS 比 #1 稍微慢一些，但允許非常快速的 update。 LOD level 低且不那麼容易被 ray 命中的動態物體。
3 yes no no trace 效能最好，但 build AS 會比 #1 和 #2 都慢。 靜態物體。
4 yes no yes trace 效能很好，只比 #3 慢一點點。AS 的 update 也只比 #2 慢一些。 重要的角色模型（如玩家主角）；LOD level 高且比較容易被相當數量的 rays 命中的動態物體。

Ray Tracing Pipeline

ray tracing pipeline 是與 graphics pipeline，compute pipeline 並列的一種新流水線，主要提供有 ray generation shader，intersection shader，和三種 hit shader 可程式化。

Ray Generation Shader

在該 shader 裡可以呼叫 TraceRay() 介面來使用 ray tracing pipeline 硬體光追：對 AS 進行 ray-traversal，並根據 intersection 的情況來自動呼叫對應的 hit shader 來完成 hit point 的著色。

TraceRay() 一般不可以在別的 shader 中呼叫，只能在 ray tracing pipeline 的相關 shader（RGS，MS，CHS之類的）中被呼叫，但一般推薦只在 RGS 中呼叫，不推薦遞迴呼叫（如 RGS 呼叫 TraceRay() 觸發 CHS，CHS 再呼叫 TraceRay()），因為遞迴呼叫往往不如改造成多輪 pass 迭代。

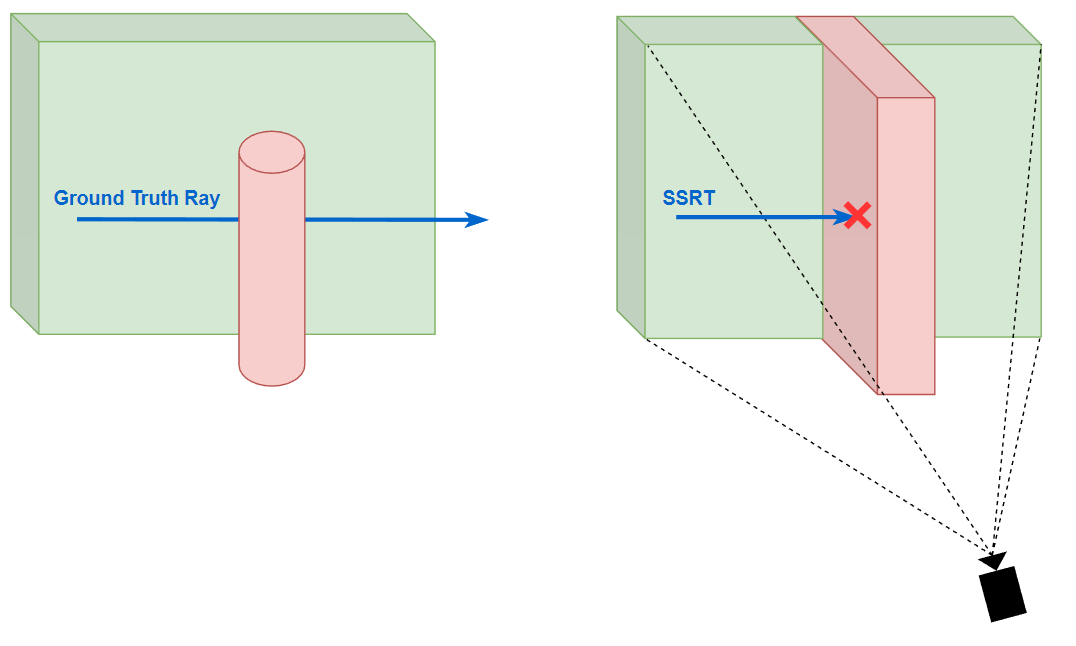
顯而易見的問題是：如果 marching 最終走出了螢幕外，那麼 SSRT 將無能為力去處理（因為只記錄了螢幕上的資訊）。並且 SSRT 的命中判斷是保守的：即 SSRT 產生 hit 了則 ground truth ray tracing 必定會產生 hit，但 SSRT miss 了但 ground truth ray tracing 不一定會 miss。

以上內容均在我以前的博文（基於螢幕空間的實時全域性光照（Real-time Global Illumination Based On Screen Space） - KillerAery - 部落格園 (cnblogs.com) ）也有大概介紹。

此外，SSRT 還有一個效果問題：由於相交檢測是簡單的深度比較，這就相當於把攝像機所看到的 depth texture 都當成了完全實心的場景，但是這樣在一些 case 下是不正確的（特別是一個小物體放進攝像機的近處，然後遮擋了大部分場景）。

但是由於 voxel 並不像球那樣中心點到表面都一樣的距離，在斜方向的情況下很容易出現 marching 後仍然停留在同一個 voxel 從而產生重複取樣。

Voxel Cone Tracing

將一堆從相同 origin 點出發的 rays 近似成一個 cone 的形式。

類似 voxel ray tracing，voxel cone tracing 累積的 alpha 值小於一定閾值則繼續 marching；不同的是隨著 marching 越來越遠離 origin 點，cone 的直徑也越來越大。而 voxel cone tracing 聰明地對 voxels 的 3d texture 生成預過濾的 mipmap：在 cone 半徑小的時候在 mipmap level 低的 voxel texture 去取樣，在 cone 半徑大時候在 mipmap level 高的 voxel texture 去取樣。

當然，本身 voxels 便是不準確的場景表達，而預過濾的 texture 更進一步會導致高頻資訊的丟失，尤其是 mipmap level 高時。因此 voxel cone tracing 往往僅適用於蒐集不那麼準確的光照。

以下是一些 voxel cone tracing 的數學關係。

一次 marching 步長 \(step\) 取決於 cone 的直徑 \(d\)：

\[step = max(d, voxelSize(level)) \]

當前應該去哪個 mipmap level 取樣 voxel 也需要取決於直徑 \(d\) ：

\[level = \log_2(\frac{d}{voxelSize(maxLevel)}) \]

而直徑 \(d\) 又取決於 marching 總共走過的距離 \(t\) 和 cone 的張角 \(ψ\)：

\[d = 2 * t * tan\frac{ψ}{2} \]

SDF Tracing / Sphere Tracing

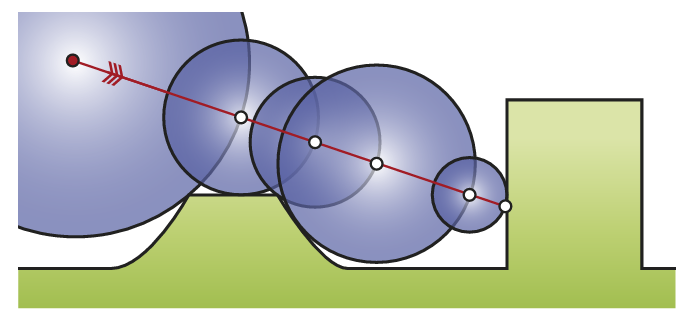
所謂的 SDF tracing（或者更正式的叫法為 sphere tracing），其實就是基於 SDF 的 ray marching。其基本原理非常簡潔，也非常聰明：從點 \(x_{0}\) 開始投射一條 ray，然後進行若干次 marching，每次 marching 的起點為上一次 marching 的終點，而 marching 的步長取為起點 \(x_{n}\) 的 SDF 值 \(f(x_n)\) 。

SDF 代表著離該點最近的幾何表面有多遠，也就是說在 SDF 值範圍內，這個 ray 絕對不會與任何幾何表面相交。

當然 \(f(x_n)\) 在有限步數下無法收斂到剛好為 0，實現中往往用一個小的閾值 $\epsilon $ 來做命中判斷。

在實踐中，最常用 3D texture 來儲存 SDF，也就是說 SDF 是以均勻網格的形式儲存的，每個 cell 儲存一個 SDF 值。容易想到，對整個場景構建高精度的 SDF 將會耗費巨量頻寬和儲存空間，並且在實時渲染領域往往是不可以承擔的。

Global SDF + Mesh SDF

UE5 Lumen 為了解決場景的 SDF 表示問題，為每個 mesh 單獨預生成了一個高精度的 sdf（稱之為 mesh sdf），然後將場景中每個 mesh sdf 實時合成一個低精度的場景 sdf（稱之為 global sdf）。

這樣就可以先在 global sdf 進行低精度的 sdf tracing，當 marching 到存在 mesh sdf 的區域時，就可以存取對應的 mesh sdf 進行高精度的 sdf tracing。

global sdf 視覺化：

  1. 對每個非空的 voxel 建立一個對應的 brick，一個 brick 就是一個所謂的 local DF，包含 8x8 個 brixels（brixel 儲存了 DF 值）。

  1. 對每個 brick，遍歷對應 voxel 的 triangle list：

    • 計算出 brick 內的 AABB box（紅線框）。
    • 先對與 triangles 有相交的 brixels 填充 DF 值（其實就是離最近三角形的距離）。

    • 而沒有相交的 brixels 在隨後使用 Eikonal / Jump flooding 演演算法來填充 DF 值。

    • 對於邊界的 brixels，則參與所有鄰接 bricks 的計算。

  2. 對計算出來的 AABB boxes 構建出一棵 3-level AABB tree，以供後續 sdf tracing 查詢使用。

Enhanced Sphere Tracing

傳統 sphere tracing 演演算法中，在點 \(x_n\) 的 ray marching 步長應取為 SDF 值 \(f(x_{n})\)，而這種 marching 其實是保守的。

實際上我們可以採用更激進的步長倍數 \(\alpha\) ，只要 \(x_n\) 的SDF 值加激進 marching 後到達 \(x_{n+1}\) 後的 SDF 值 \(f(x_{n+1})\) 大於本次激進 marching 的步長 \(\alpha f(x_n)\)（即 \(f(x_n) + f(x_{n+1}) > \alpha f(x_{n})\)，在幾何上實際就是表現為兩個 sphere 相交），那麼就說明 ray 可以安全通過本次激進 marching，否則應當退回到點 \(x_n\) 的位置重新進行保守的 marching。

當然，過於激進的步長倍數會導致過多的回退，而過保守的步長倍數則不會帶來效率的提升，因此應該針對自己的場景調整 \(\alpha\) 引數（引入一些動態調整 \(\alpha\) 的方法，如下面的 accelerating sphere tracing），而原 paper 的作者推薦大約 \(\alpha = 1.2\) 倍步長為效能最佳。

Accelerating Sphere Tracing

更進一步的激進策略是：永遠假設前兩次 marching 所形成的 sphere 都相切於同一平面，那麼下一次可以嘗試 marching 這樣一個 sphere：與該平面相切，也剛好與上一次的 marching sphere 相切；如果嘗試失敗則回退至保守 marching。

那這個嘗試 marching 的具體步長應該是多少呢？

由相似三角形易得 \(\frac{d_i}{r_i+r_{i+1}}=\frac{r_{i-1}-r_i}{r_i-r_{i+1}}\)

那麼嘗試的步長應為：

\[d_{i+1}=r_{i+1}+r_i=r_i \cdot \frac{2 d_i}{d_i+r_{i-1}-r_i} \]

這種策略比 enhanced sphere tracing 回退次數減少了許多，有更好的加速效果。

Segment Tracing

一堆數學定義（如 Lipschitz），還要假設場景是 \(C^2\) 連續（如果有稜角基本就容易出問題），並且不一定有優化（甚至可能是負優化，因為需額外多次取樣 SDF 來求導），不推薦用。

實在好奇，也可以這樣感性地理解：segment tracing 實際上就是在 ray 的方向分成一段段線段（segment），然後算 segment 的頂點和末尾點的 SDF 一階導，並由此推算出這段 segment 附近的大概安全區域（SDF 一階導相當於往最近表面的反方向，由兩個導數資訊就可以推算出大概的表面資訊），並算出 ray 如果要經過這塊區域，其最遠的安全步長是多少。

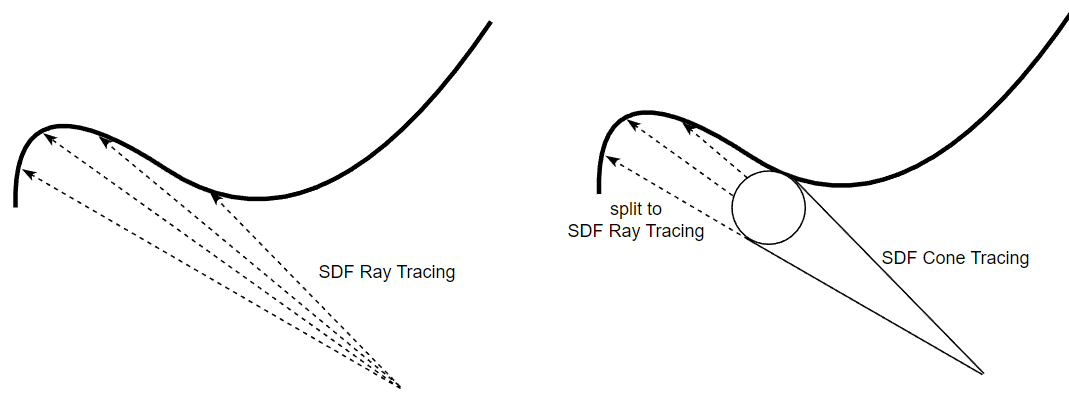
SDF Cone Tracing

如果有多條從相同起點出發且出射方向相近的 rays，可以將它們合併成一個 cone，先進行 SDF cone tracing，hit 到物體時再分裂成原始的多條 rays 並分別進行 SDF ray tracing。

一個優化方式是：我們可以進行多次非透明的 ray query（需要設定 RayFlags 為 Opaque）：每次 ray query 產生 intersection 就 commit，然後做 alpha 相關測試（和上面一樣），如果還需要繼續 ray tracing，那就更新發射點位置為 intersection 的位置並進行新一次的 ray query。

這個優化方式的效能往往能提升2倍甚至更多的效能，一方面是 RayFlags 設定成 Opaque 後 ray query 的流程會簡化很多，另一方面是因為 ray query 是特定的硬體流程，中斷返回會導致額外的 latency，因此儘量讓 ray query always commit。

Material Ray

而除了計算直接光照以外，我們還往往需要計算著色點受到的間接光照，這時候往往需要投射 material ray，獲取 hit point 的材質資訊以計算 radiance：

對於硬體光追 ray tracing pipeline 來說，material ray 是容易實現的：直接通過 closest hit shader 來計算出 hit point 的材質資訊，並之後通過 payload 來獲取材質資訊即可。

  1. 若著色點位於螢幕範圍內，可以優先嚐試 screen space ray tracing，若命中則可以獲取螢幕上的 normal, albedo, color 等材質資訊。
  2. 若著色點不在螢幕範圍內亦或者 SSRT 沒命中，則可以使用 visibility ray + material cache：由於缺少 closest hit shader，我們只能通過投射 visibility ray 得到一個 hit point 的 position，而得不到幾何資訊或者材質資訊。但是我們可以藉助 material cache（例如：lumen 裡的 mesh card；voxels 等）來獲取 hit point 的材質資訊。

注：幾何資訊有部分還是可以強行獲得的，如通過 SDF 梯度算 normal ，或者 triangle id 獲取 3 個 vertex 從而算出 face normal 等。

Low-Accuracy Ray + Short Ray

參考