第十二章 璣鏤（扭索）紋

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

譯者：池中物王二狗(sheldon)

原始碼：github: https://github.com/willian12345/coding-curves

曲線藝術程式設計系列 第 12 章

璣鏤紋是一種錯綜複雜且非常迷人的圖案。它經常被繪製在銀行鈔票和官方檔案上，你也可以在手錶錶盤或其它複雜機械上找到它們的身影。正因為它們如此複雜難以理解，所以它們經常被鐫刻在金屬表面，這通常是由機器來完成。想象一下一臺高階螺旋儀用金屬刻蝕工具代替原本用於繪圖的圓珠筆。「璣鏤紋」 這詞相當模糊，它可以代稱所有這一類紋理。我將要講解的是如下圖案中的璣鏤紋理：

這個紋理你可能已經在某種證書或鈔票上見過了，一旦你知道生成原理，你就可以以調整程式碼的方式生成另外相似的紋理圖案。

第一步：建立一個單獨的圓

我們先從建立單個簡單的圓開始，它看起來應該像下面這樣：

它非常像一個擺線或玫瑰曲線。事實上你可以通過它們的公式建立它，但我將改動一點點，以便後面處理更復雜的紋理圖案。

本質上是一個正弦波包住一個圓。注意它有一個內半徑和一個外半徑。 這個正弦波有 80 個 nodes，它自身波紋會重疊。為了更好的解析，我將增大內半徑讓它不再重疊：

現在可以看的更清楚了。正如我所說的那樣，一個正弦波包住一個圓。現在我要再加一點點重疊紋理：

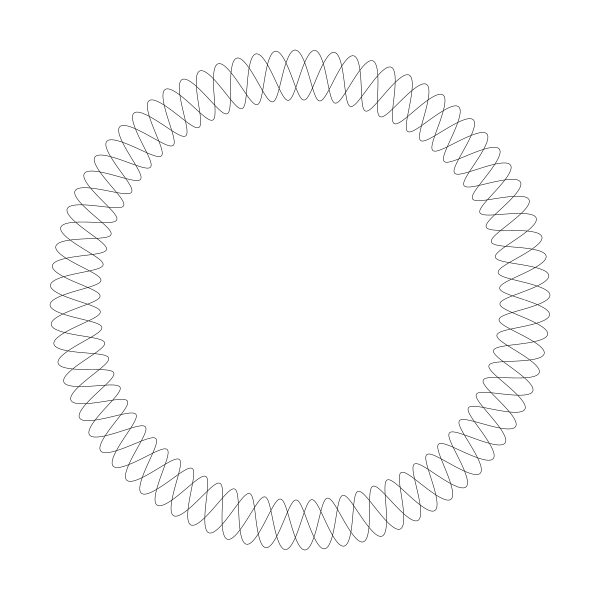
圖中雖然有重疊部分你仍然可以觀察到正弦波。第一張影象用的是同樣的原理，只是內半徑更小且重疊部分更多。現在我讓我們看看是如何繪製的。

我們先設內半徑 inner 與外半徑 outer 開始。通過簡單的數學運算得到 mid 半徑。它將是正弦波的零點。我們還需要一個範圍，它決定了正弦波在內外半徑擴充套件的範圍。你也可以稱它為這個正弦波的振幅。

width = 600
height = 600
canvas(width, height)
 
translate(width / 2, height / 2)
 
inner = 50
outer = 250
range = (outer - inner) * 0.5
mid = inner + range

下一步，我們需要知道要多少個波形週期，還有多少次重疊。我將把它們稱作 nodes 和 div, 它們應該是整數且兩個數不能被整除。 這非常像上一章玫瑰曲線中遇到的 n 和 d 引數， 但為了不混淆我會用另外的變數名。

nodes = 80
div = 11

現在我們可以迴圈 t 到 2 * PI * div 並繪製一些線段。 下一個線段座標點角度簡單的用 t 和 半徑 radius 計算得出。我們需要將回圈結束條件 2 * PI 再乘以 div 以確保足夠繞一圈，首尾可以相連。

for (t = 0; t < 2 * PI * div; t += 0.01) {
  radius = mid + sin(t * nodes / div) * range
  x = cos(t) * radius
  y = sin(t) * radius
  lineTo(x, y)
}
stroke()

如果你回頭看玫瑰曲線那一章， 你會發現它們都是用相似的方法計算半徑值的， 但相比使用正弦和單一的乘法，我們使用 mid 和 range 調整半徑至內半徑與外半徑之間。

你可以多玩玩。試試改動不同的引數。為了生成一個比較好看的璣鏤紋，你可能需要將 nodes 設高一點，div 低一點。最重要的是它們的值不能被整除。想要得到比較得體的圖案，一個比較簡單的方法是讓 div 是一個小的質數， nodes 不能是 div 的倍數。

舉個例子，如果 div 是 17，你不應該將 nodes 設為 170，否則你將會得到如下圖：

但將 nodes 增加到 171 則會得到很好的圖案：

如果你想玩的話，我幾年前做了一個可互動的版本：

https://bit101.github.io/lab/dailies/170120.html

接下來，我們在混合當中再新增一些複雜性。相比在固定的內外半徑來回繪製正弦波，我們在內外半徑各自新增正弦波變化！結果如下圖：

為此我們需要更多的引數。為了計算出最終外半徑上任意一點，我們需要基於外半徑，計算有多少正弦波週期和最終外半徑與基礎外半徑的距離差。那麼內半徑同樣需要3個值，nodes 與 div 也依然要。上圖中我使用的引數值如下：

inner = 100.0
n0 = 7.0
h0 = 10.0
 
outer = 250.0
n1 = 17.0
h1 = 20.0
 
nodes = 142.0
div = 89.0

內半徑有 7 nodes, 半徑範圍在 90 - 110 之間，它是基於100 加減 10。然後，同樣，外半徑有 17 個 nodes ，半徑範圍在 230 - 270 之間。

在 for 迴圈迭代內之前計算 "mid radius" 的相關程式碼用這些值重寫。

for (t = 0; t < 2 * PI * div; t += 0.01) {
  r0 = inner + sin(t * n0) * h0
  r1 = outer + sin(t * n1) * h1
 
  range = (r1 - r0) * 0.5
  mid = r0 + range
 
  radius = mid + sin(t * nodes / div) * range
  x = cos(t) * radius
  y = sin(t) * radius
  lineTo(x, y)
}
stroke()

當然你可以對以上程式碼進行簡化，但為了清晰起見我把每步都寫出來了。

你可以繼續改動這些引數，看看能創造出什麼樣的圖形。我們還有更復雜的一級要處理。

https://bit101.github.io/lab/dailies/170121.html

第三步 多環

下一步是創造多環，這些環相互配合在一起， 就像章節開頭的那張圖：

它的實現比看起來人簡單的多。如果你想繪製小環外圍繞大環，你僅需要將小環的外半徑作為大環的內半徑。由於我們會多次呼叫相同的程式碼，最好把它變成可複用的函數。基本上就是把 for 迴圈和 stroke 呼叫 放入一個可傳所有引數函數中。我還新增了 x, y 引數， 這樣你就可以把圖繪製在 canvas 的任意位置了。

function guilloche(x, y, ir, n0, h0, or, n1, h1, nodes, div) {
  for (t = 0; t < 2 * PI * div; t += 0.01) {
    r0 = ir + sin(t * n0) * h0
    r1 = or + sin(t * n1) * h1
 
    range = (r1 - r0) * 0.5
    mid = r0 + range
 
    radius = mid + sin(t * nodes / div) * range
    lineTo(x +cos(t) * radius, y +sin(t) * radius)
  }
  stroke()
}

我把 canvas 寬高調整為 800x800 並且像下面這樣呼叫程式碼：

guillloche(400, 400, 50, 6, 10, 120, 12, 20, 137, 37)
guillloche(400, 400, 120, 12, 20, 220, 18, 30, 141, 41)
guillloche(400, 400, 220, 18, 30, 350, 24, 20, 164, 53)

This resulted in the following image:

結果如圖：

注意第一行呼叫，外半徑引數是 120， 12，和 20。 這些作為下一個呼叫的內半徑引數。第二個呼叫的外半徑引數 220， 18 和 30， 作為最後一個呼叫的內半徑引數。像這樣做後，繪製出的環簡直完美。

像往常一樣你應該多調調引數，多試試。你可以想加多少環就加多少環。你也許希望把所有半徑引數封裝成自定義型別結構體讓這部分變的更有複用性。我將把這部分工作留給你。

另外你可能想給各個一覺不同的顏色：

(譯者注：我新增了隨機顏色原始碼在 https://github.com/willian12345/coding-curves/tree/main/examples/ch12/guilloche-colorful.html)

這裡有一個可互動的最終版本：

https://bit101.github.io/lab/dailies/170122.html

注意，這裡可沒有說環與環之間必須要緊密相扣。你可以試著給它們之間留點距離或者讓它們重疊一部分看看你能創造出多有趣的圖案。下一個例子中，第一個與最後一個環與之前例子中設定的一樣， 但中間這個環的引數定義的相當不同：

guillloche(400, 400, 20, 4, 5, 120, 8, 10, 137, 37)
guillloche(400, 400, 160, 5, 24, 160, 11, 24, 80, 17)
guillloche(400, 400, 220, 18, 16, 350, 10, 20, 164, 53)

此處，內外半徑值相等，都是 160，生成比簡單的離散環更有趣的團狀環。

還有，別忘了把它做成動畫！

總結

你用 Guilloche patterns 關鍵詞搜尋圖片，會得到非常多不同樣式的圖，大部分比我這裡講的要複雜的多。我只是從中挑了一個來講。

也許你想嘗試修改程式碼繪製其它形狀的璣鏤紋，也許從橢圓形璣鏤是個不錯的開始。然後再開始繪製其它形狀。但這些內容都超出本章範圍了。

本章 Javascript 原始碼 https://github.com/willian12345/coding-curves/blob/main/examples/ch12

---

部落格園: http://cnblogs.com/willian/
github: https://github.com/willian12345/