A First course in FEM —— matlab程式碼實現求解傳熱問題(穩態)
2023-06-18 18:00:31
這篇文章會將FEM全流程走一遍,包括網格、矩陣組裝、求解、後處理。內容是大三時的大作業,今天拿出來回顧下。
1. 問題簡介

假設為穩態,那麼葉片內導熱微分方程為:
內部區域: 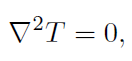 (擴散方程)
(擴散方程)
邊界:
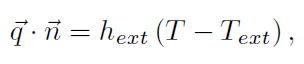 (外表面)
(外表面)
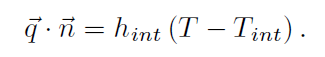 (內部冷卻孔)
(內部冷卻孔)
2.模型
2.1幾何模型
我們簡化為二維模型,如下圖所示:
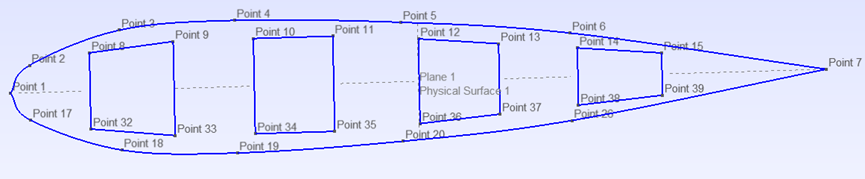

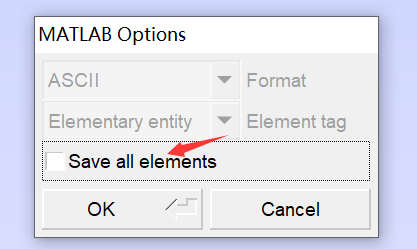
生成網格後匯出為「blademesh.m」用以後續使用,注意不要勾選Save all elements,否則會沒有邊界資訊。
我用gmsh-4.4.1-Windows64版本,可以匯出邊界資訊。但是新版的gmsh匯出為.m檔案時,邊界資訊無法儲存。
3. 矩陣組裝
3.1 控制方程
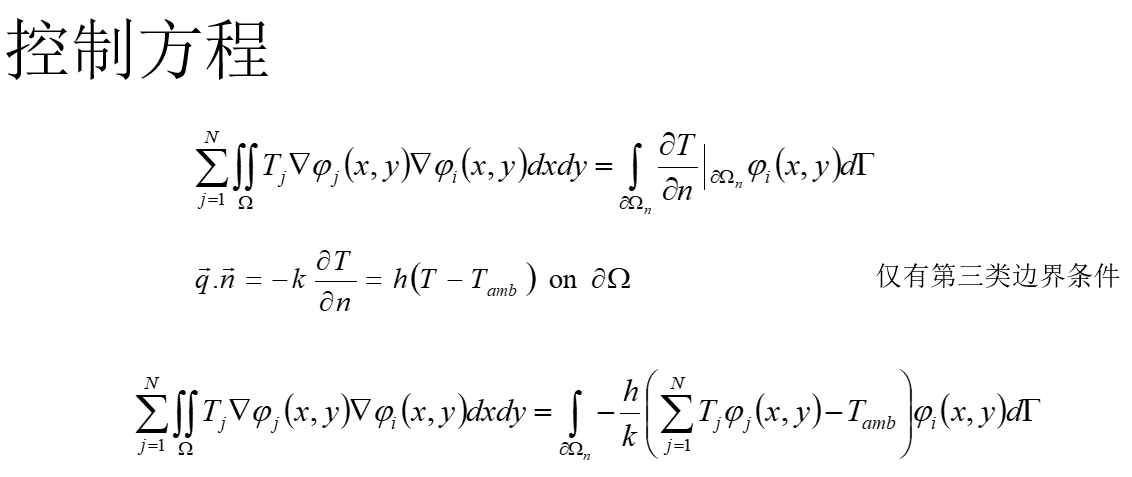
3.2 系統矩陣

其中的Ω代表全域,我們將全域分解為一個個單元,這就是有限元的思想。
計算每個單元(Ωe)的剛度矩陣,然後每項加到整體剛度矩陣:
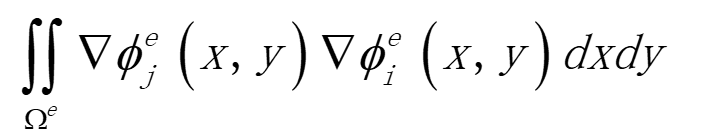
4. 程式碼實現(matlab)
|
步驟 |
工具或函數 |
|
定義求解域並生成網格 |
gmsh匯出網格為blademesh.m |
|
讀入網格資訊,資料轉換 |
bladeread |
|
矩陣和向量組裝,線性方程組求解 |
bleadheat |
|
檢視結果 |
bladeplot |
主程式:bladeheat.m
% Clear variables clear all; % Set gas temperature and wall heat transfer coefficients at % boundaries of the blade. Note: Tcool(i) and hwall(i) are the % values of Tcool and hwall for the ith boundary which are numbered % as follows: % % 1 = external boundary (airfoil surface) % 2 = 1st internal cooling passage (from leading edge) % 3 = 2nd internal cooling passage (from leading edge) % 3 = 3rd internal cooling passage (from leading edge) % 3 = 4th internal cooling passage (from leading edge) % Tcool = [1300, 200, 200, 200, 200]; % hwall = [14, 4.7, 4.7, 4.7, 4.7]; Tcool = [1573, 473, 473, 473, 473]; h = [205.8*10^-6, 65.8*10^-6, 65.8*10^-6, 65.8*10^-6, 65.8*10^-6]; k = 14.7*10^-3; hwall = h / k; % Load in the grid file % NOTE: after loading a gridfile using the load(fname) command, % three important grid variables and data arrays exist. These are: % % Nt: Number of triangles (i.e. elements) in mesh % % Nv: Number of nodes (i.e. vertices) in mesh % % Nbc: Number of edges which lie on a boundary of the computational % domain. % % tri2nod(3,Nt): list of the 3 node numbers which form the current % triangle. Thus, tri2nod(1,i) is the 1st node of % the i'th triangle, tri2nod(2,i) is the 2nd node % of the i'th triangle, etc. % % xy(2,Nv): list of the x and y locations of each node. Thus, % xy(1,i) is the x-location of the i'th node, xy(2,i) % is the y-location of the i'th node, etc. % % bedge(3,Nbc): For each boundary edge, bedge(1,i) and bedge(2,i) % are the node numbers for the nodes at the end % points of the i'th boundary edge. bedge(3,i) is an % integer which identifies which boundary the edge is % on. In this solver, the third value has the % following meaning: % % bedge(3,i) = 0: edge is on the airfoil % bedge(3,i) = 1: edge is on the first cooling passage % bedge(3,i) = 2: edge is on the second cooling passage % bedge(3,i) = 3: edge is on the third cooling passage % bedge(3,i) = 4: edge is on the fourth cooling passage % bladeread; % Start timer Time0 = cputime; % Zero stiffness matrix K = zeros(Nv, Nv); b = zeros(Nv, 1); % Zero maximum element size hmax = 0; % Loop over elements and calculate residual and stiffness matrix for ii = 1:Nt, kn(1) = tri2nod(1,ii); kn(2) = tri2nod(2,ii); kn(3) = tri2nod(3,ii); xe(1) = xy(1,kn(1)); xe(2) = xy(1,kn(2)); xe(3) = xy(1,kn(3)); ye(1) = xy(2,kn(1)); ye(2) = xy(2,kn(2)); ye(3) = xy(2,kn(3)); % Calculate circumcircle radius for the element % First, find the center of the circle by intersecting the median % segments from two of the triangle edges. dx21 = xe(2) - xe(1); dy21 = ye(2) - ye(1); dx31 = xe(3) - xe(1); dy31 = ye(3) - ye(1); x21 = 0.5*(xe(2) + xe(1)); y21 = 0.5*(ye(2) + ye(1)); x31 = 0.5*(xe(3) + xe(1)); y31 = 0.5*(ye(3) + ye(1)); b21 = x21*dx21 + y21*dy21; b31 = x31*dx31 + y31*dy31; xydet = dx21*dy31 - dy21*dx31; x0 = (dy31*b21 - dy21*b31)/xydet; y0 = (dx21*b31 - dx31*b21)/xydet; Rlocal = sqrt((xe(1)-x0)^2 + (ye(1)-y0)^2); if (hmax < Rlocal), hmax = Rlocal; end % Calculate all of the necessary shape function derivatives, the % Jacobian of the element, etc. % Derivatives of node 1's interpolant dNdxi(1,1) = -1.0; % with respect to xi1 dNdxi(1,2) = -1.0; % with respect to xi2 % Derivatives of node 2's interpolant dNdxi(2,1) = 1.0; % with respect to xi1 dNdxi(2,2) = 0.0; % with respect to xi2 % Derivatives of node 3's interpolant dNdxi(3,1) = 0.0; % with respect to xi1 dNdxi(3,2) = 1.0; % with respect to xi2 % Sum these to find dxdxi (note: these are constant within an element) dxdxi = zeros(2,2); for nn = 1:3, dxdxi(1,:) = dxdxi(1,:) + xe(nn)*dNdxi(nn,:); dxdxi(2,:) = dxdxi(2,:) + ye(nn)*dNdxi(nn,:); end % Calculate determinant for area weighting J = dxdxi(1,1)*dxdxi(2,2) - dxdxi(1,2)*dxdxi(2,1); A = 0.5*abs(J); % Area is half of the Jacobian % Invert dxdxi to find dxidx using inversion rule for a 2x2 matrix dxidx = [ dxdxi(2,2)/J, -dxdxi(1,2)/J; ... -dxdxi(2,1)/J, dxdxi(1,1)/J]; % Calculate dNdx dNdx = dNdxi*dxidx; % Add contributions to stiffness matrix for node 1 weighted residual K(kn(1), kn(1)) = K(kn(1), kn(1)) + (dNdx(1,1)*dNdx(1,1) + dNdx(1,2)*dNdx(1,2))*A; K(kn(1), kn(2)) = K(kn(1), kn(2)) + (dNdx(1,1)*dNdx(2,1) + dNdx(1,2)*dNdx(2,2))*A; K(kn(1), kn(3)) = K(kn(1), kn(3)) + (dNdx(1,1)*dNdx(3,1) + dNdx(1,2)*dNdx(3,2))*A; % Add contributions to stiffness matrix for node 2 weighted residual K(kn(2), kn(1)) = K(kn(2), kn(1)) + (dNdx(2,1)*dNdx(1,1) + dNdx(2,2)*dNdx(1,2))*A; K(kn(2), kn(2)) = K(kn(2), kn(2)) + (dNdx(2,1)*dNdx(2,1) + dNdx(2,2)*dNdx(2,2))*A; K(kn(2), kn(3)) = K(kn(2), kn(3)) + (dNdx(2,1)*dNdx(3,1) + dNdx(2,2)*dNdx(3,2))*A; % Add contributions to stiffness matrix for node 3 weighted residual K(kn(3), kn(1)) = K(kn(3), kn(1)) + (dNdx(3,1)*dNdx(1,1) + dNdx(3,2)*dNdx(1,2))*A; K(kn(3), kn(2)) = K(kn(3), kn(2)) + (dNdx(3,1)*dNdx(2,1) + dNdx(3,2)*dNdx(2,2))*A; K(kn(3), kn(3)) = K(kn(3), kn(3)) + (dNdx(3,1)*dNdx(3,1) + dNdx(3,2)*dNdx(3,2))*A; end % Loop over boundary edges and account for bc's % Note: the bc's are all convective heat transfer coefficient bc's % so the are of 'Robin' form. This requires modification of the % stiffness matrix as well as impacting the right-hand side, b. % for ii = 1:Nbc, % Get node numbers on edge kn(1) = bedge(1,ii); kn(2) = bedge(2,ii); % Get node coordinates xe(1) = xy(1,kn(1)); xe(2) = xy(1,kn(2)); ye(1) = xy(2,kn(1)); ye(2) = xy(2,kn(2)); % Calculate edge length ds = sqrt((xe(1)-xe(2))^2 + (ye(1)-ye(2))^2); % Determine the boundary number bnum = bedge(3,ii) + 1; % Based on boundary number, set heat transfer bc K(kn(1), kn(1)) = K(kn(1), kn(1)) + hwall(bnum)*ds*(1/3); K(kn(1), kn(2)) = K(kn(1), kn(2)) + hwall(bnum)*ds*(1/6); b(kn(1)) = b(kn(1)) + hwall(bnum)*ds*0.5*Tcool(bnum); K(kn(2), kn(1)) = K(kn(2), kn(1)) + hwall(bnum)*ds*(1/6); K(kn(2), kn(2)) = K(kn(2), kn(2)) + hwall(bnum)*ds*(1/3); b(kn(2)) = b(kn(2)) + hwall(bnum)*ds*0.5*Tcool(bnum); end % Solve for temperature Tsol = K\b; % Finish timer Time1 = cputime; % Plot solution bladeplot; % Report outputs Tmax = max(Tsol); Tmin = min(Tsol); fprintf('Number of nodes = %i\n',Nv); fprintf('Number of elements = %i\n',Nt); fprintf('Maximum element size = %5.3f\n',hmax); fprintf('Minimum temperature = %6.1f\n',Tmin); fprintf('Maximum temperature = %6.1f\n',Tmax); fprintf('CPU Time (secs) = %f\n',Time1 - Time0);
bladeread.m
% Read three important grid variables and data arrays % Nt: Number of triangles (i.e. elements) in mesh % Nv: Number of nodes (i.e. vertices) in mesh % Nbc: Number of edges which lie on a boundary of the computational % domain. % tri2nod(3,Nt): list of the 3 node numbers which form the current % triangle. Thus, tri2nod(1,i) is the 1st node of % the i'th triangle, tri2nod(2,i) is the 2nd node % of the i'th triangle, etc. % xy(2,Nv): list of the x and y locations of each node. Thus, % xy(1,i) is the x-location of the i'th node, xy(2,i) % is the y-location of the i'th node, etc. % bedge(3,Nbc): For each boundary edge, bedge(1,i) and bedge(2,i) % are the node numbers for the nodes at the end % points of the i'th boundary edge. bedge(3,i) is an % integer which identifies which boundary the edge is % on. In this solver, the third value has the % following meaning: % % bedge(3,i) = 0: edge is on the airfoil % bedge(3,i) = 1: edge is on the first cooling passage % bedge(3,i) = 2: edge is on the second cooling passage % bedge(3,i) = 3: edge is on the third cooling passage % bedge(3,i) = 4: edge is on the fourth cooling passage % clc run('blademesh.m'); Nv=msh.nbNod; Nt=size(msh.TRIANGLES,1); Nbc=size(msh.LINES,1); for i=1:Nt tri2nod(1,i)=msh.TRIANGLES(i,1); tri2nod(2,i)=msh.TRIANGLES(i,2); tri2nod(3,i)=msh.TRIANGLES(i,3); end for i=1:Nv xy(1,i)=msh.POS(i,1); xy(2,i)=msh.POS(i,2); end for i=1:Nbc bedge(1,i)=msh.LINES(i,1); bedge(2,i)=msh.LINES(i,2); bedge(3,i)=msh.LINES(i,3); end
bladeplot.m
% Plot T in triangles figure; for ii = 1:Nt, for nn = 1:3, xtri(nn,ii) = xy(1,tri2nod(nn,ii)); ytri(nn,ii) = xy(2,tri2nod(nn,ii)); Ttri(nn,ii) = Tsol(tri2nod(nn,ii)); end end HT = patch(xtri,ytri,Ttri); axis('equal'); set(HT,'LineStyle','none'); title('Temperature (K)'); % caxis([298,1573]); colormap(jet); HC = colorbar; hold on; bladeplotgrid; hold off;
5. 計算結果
