第十一章 玫瑰花形 ROSES

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

譯者：池中物王二狗(sheldon)

原始碼：github: https://github.com/willian12345/coding-curves

曲線藝術程式設計系列第 11 章

這一篇我們將看到另一種我鐘意的曲線型別 -- 玫瑰花形或玫形曲線。 在我看來這類曲線就像是圓形的利薩茹曲線 Lissajous curves，或者非常規則的諧波圖。事實上它們是一類特別的長短幅內擺線，特別到足夠自成一類。先給你看些例子，下面是玫形曲線：

（譯都注：這是玫瑰花 roses 我是不信的...）

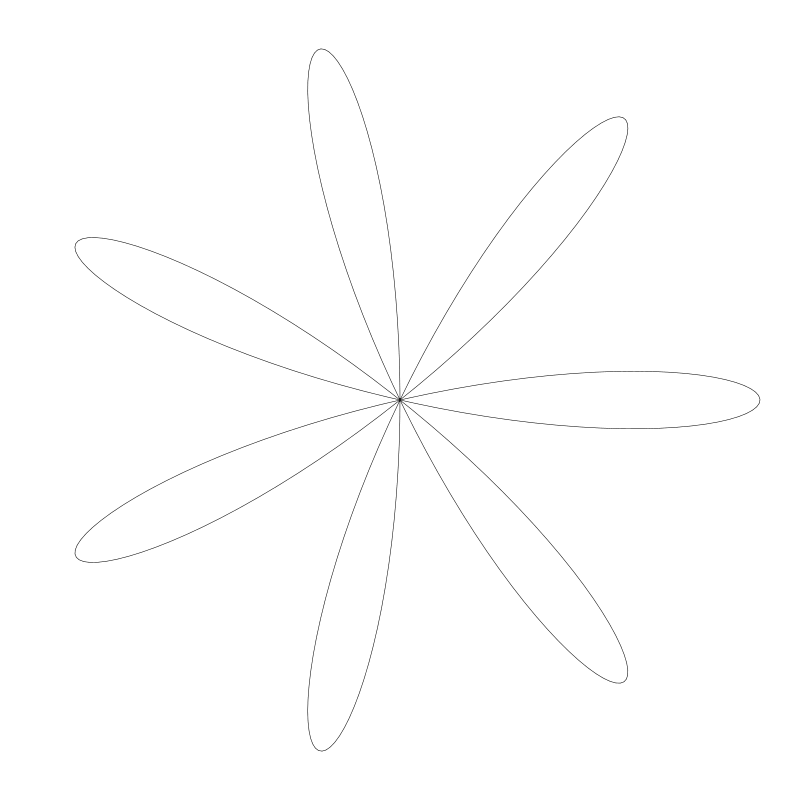
就像其它我們關注過的其它曲線一樣，我們有引數方程, 用 t 從 0 到 2 * PI 遞增，計算得到返回值並用它繪製出曲線。我們先往回看看圓的方程：

function circle(x, y, r) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    x1 = x + cos(t) * r
    y1 = y + sin(t) * r
    lineTo(x1, y1)
  }
}

你當然可以對 for 迴圈內的程式碼簡化成一行，但為了解釋的更清晰我還是將它展開了。

一個玫瑰花形曲線使用同樣的策略，但使用以 t 和其它引數為基礎的動態半徑取代固定的半徑。下面是半徑方程：

r = a * cos(n * t)

現在我們有了 2 個新變數。a 是花的覆蓋半徑， n 控制著花瓣數（當然花瓣數量的計算有點兒複雜，捎後回來解釋）。現在我們可以建立一個玫瑰花形函數：

function rose(x, y, a, n) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    r = a * cos(n * t)
    x1 = x + cos(t) * r
    y1 = y + sin(t) * r
    lineTo(x1, y1)
  }
}

當然如果你願意，可以整理一下程式碼：

function rose(x, y, a, n) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    r = a * cos(n * t)
    lineTo(x + cos(t) * r, y + sin(t) * r)
  }
}

現階段先假設函數的 n 引數為正整數。當然後面我們也會探索更大的範圍。

現在我們就可以繪製我們第一個玫瑰花形：

width = 800
height = 800
canvas(800, 800)
 
rose(width / 2, height / 2, width * 0.45, 5)
stroke()

在這裡我會經常用 width * 0.45。它剛好比 canvas 寬度的一半小一點兒，這讓曲線幾乎剛好覆蓋整個 canvas 但又沒能碰到邊界。

上面程式碼會生成一個 5 個花瓣的玫瑰花形：

第一個例子中 n 用的是 7。 而下面這個花 n 用的是 11：

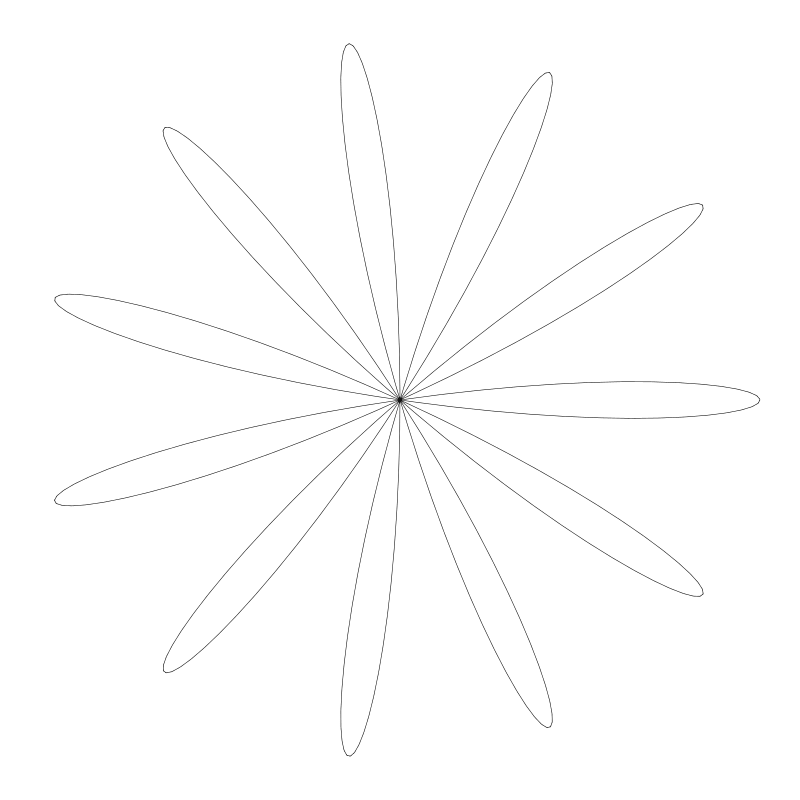
到目前為止我們可以看到 n 與 花瓣數量之間有很好的相關性。前面 n 用的都是奇數。如果我們用的是偶數 n 為 4 會如何呢？

有意思，產生了 8 個花瓣。n 的值遵循 奇數 n 建立 n 個花瓣。 偶數 n 建立 2 * n 個花瓣。把 n 再設大一點看看，設 n = 40，它將產生 80 個花瓣。我不得不提升辨率 -- 將回圈上的 t 改為 0.001 以保證花瓣沒有鋸齒。

相反，如果 n = 1，僅會得到一個單圓

有點怪，但在數學上說得通。你會發現 n 為負值時，玫瑰花看起來與 n 為正值時得到的結果圖形一樣。 下面左邊的是 5 右邊的是 -5

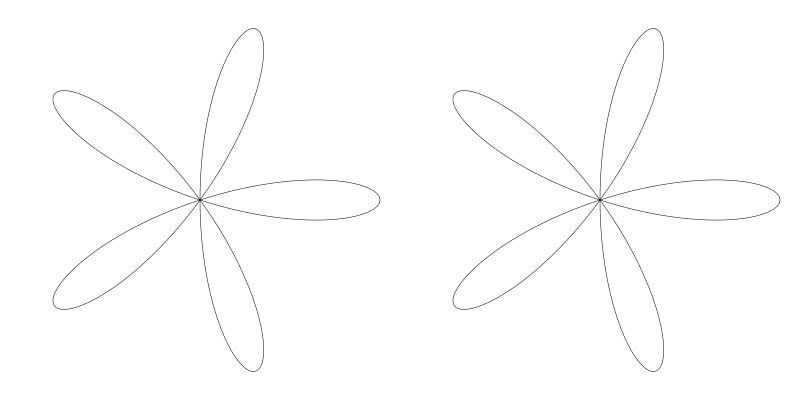
毫無意外， n = 0 時會得不到任何圖形。並且我們已經覆蓋了全部的整數玫瑰花形。如果這是全部了的話就太好了。可惜還有更多的型別。
（譯者注：如果你用 javascript 程式碼實現測試，你會發現 n = 0 時你會畫出一個大圓，n = 1 時是右側一個小圓，
可用原始碼 https://github.com/willian12345/coding-curves/tree/main/examples/ch11/rose-3.html 測試）

交替玫瑰花形

在我講完所有 n 值前， 我想先提一下交替玫瑰方程。在半徑方程中用正弦 sine 代替餘弦 cosine ：

r = a * sin(n * t)

它會生成與原來一樣的花形，但是旋轉了。左側是用餘弦 5 個花瓣的原圖， 右側是用正弦：

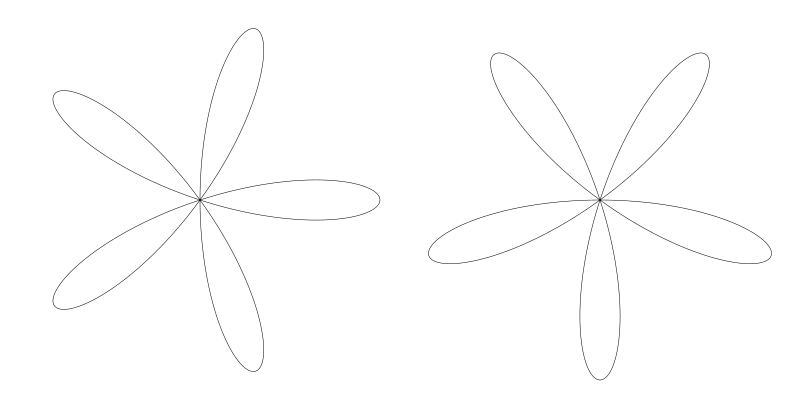
8 個花瓣的也是一樣的效果 （n = 4）

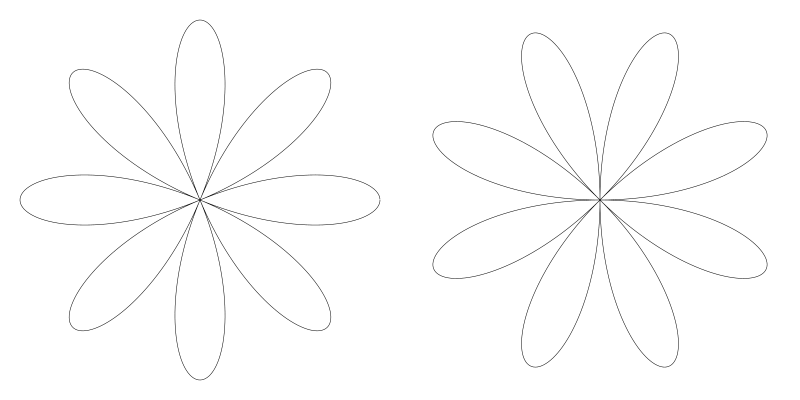
真實的旋轉值是 PI / （2 * n) 弧度, 或 90 / n 度。n 為奇數時，視覺上看起來總是旋轉了 90 度 （實際旋轉可能不同，但由於旋轉對稱性，它看起來就像是旋轉了90度）。當 n 為偶數時花瓣就會在原版本花瓣之間。

當 n 為分數

當我們給 n 的值是分數時事情就變的更有趣了。我們可以試著用分數生成玫瑰花 ：

rose(width/2, height/2, width * 0.45, 5.0 / 4.0)
stroke()

但是結果越令人相當失望

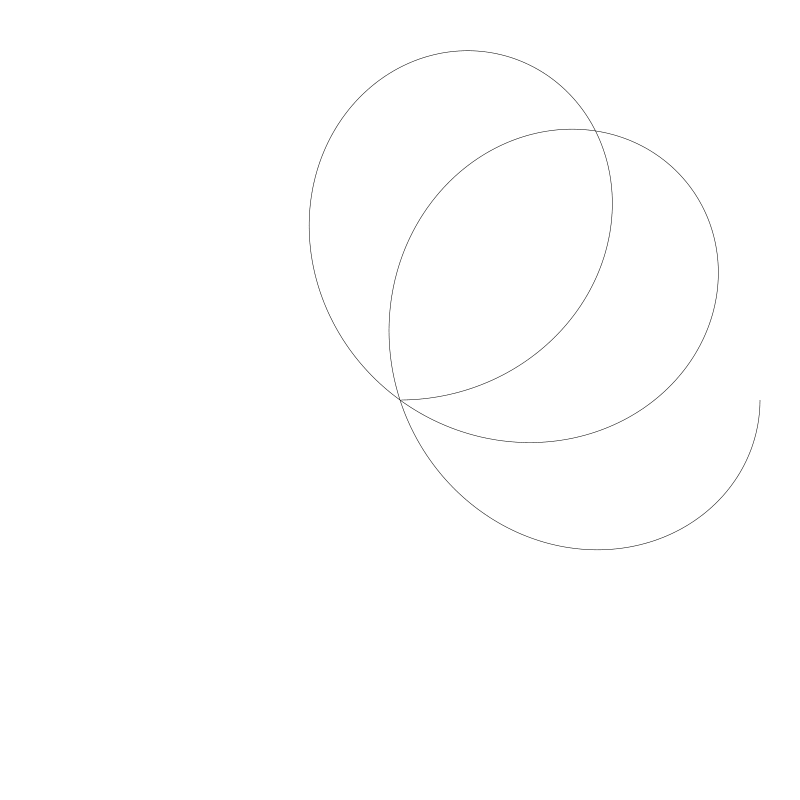
問題在於它需要超過 2 * PI 以獲取整圓。那麼要超過多少呢？ 好吧，我們用程式設計的方式來解決，我們首先需要確保 n 為有理數。如果它是無理數， 這朵玫瑰花就會無法閉合回起點（譯者注：繞多少圈圓也無法與起始點相接）。我們也需要知道分數的分子與分母。我們可以通過調整玫瑰花形生成函數，為其額外新增一個引數，我們將 n 作為分子，d 作為分母。

rose(x, y, a, n, d) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    r = a * cos(n / d * t)
    lineTo(x + cos(t) * r, y + sin(t) * r)
  }
}

調整後的函數暫時還沒有解決問題，但這是解決問題的第一步。你可以強制 n 和 d 為整數，以確保得到有理數分數（譯者注：數學上，有理數是一個整數 a 和一個 正整數 b 的比）， 但確保相除前轉換它們以保證它返回值為浮點數。

現在需要調整 for 迴圈 2*PI 的結束條件為我們需要的值。 這個範圍值是：

limit = PI * d * m

但是這個新的 m 變數是什麼？如果 d * n 結果為奇數則 m 應該為 1。如果 d * n 結果為偶數則 m 應該為 2。 Woo! 有點兒複雜了.. 別擔心我們可以簡化它。

我們通常將數對2取餘來判斷數的奇偶性。如果結果為 0 ，則這個數是偶數，如果結果為 1 則原值為奇數。 我們想：

m = 1 when d * n % 2 == 1

並且

m = 2 when d * n % 2 == 0

所以我們可以這樣設定：

（譯者注： d * n % 2 == 1 奇數 m = 1; d * n % 2 == 0 偶數 m = 2; ）

m = 2 - d * n % 2

下面是修改後的函數：

rose(x, y, a, n, d) {
  m = 2 - d * n % 2
  limit = PI * d * m
  for (t = 0; t < limit; t += 0.01) {
    r = a * cos(n / d * t)
    lineTo(x + cos(t) * r, y + sin(t) * r)
  }
}

記住，如果 n 和 d 強制為整數， 為了保證執行正常你可能需要對它們強制轉換。我將這部分工作留給你們自己完成 。現在我們可以重新呼叫：

rose(width/2, height/2, width * 0.45, 5, 4)
stroke()

現在得到的結果就好多了：

（譯者注：可用原始碼 https://github.com/willian12345/coding-curves/tree/main/examples/ch11/rose-6.html 測試）

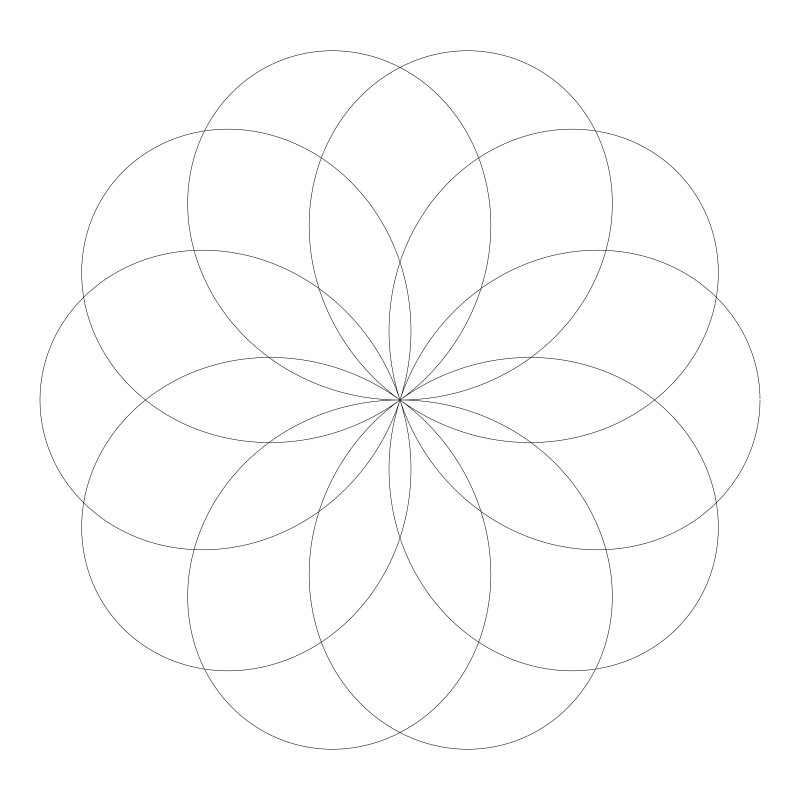
這回這玫瑰花算是完整了。

現在你可以用不同的分數來測試下效果了。我發現如果分子分母值大但相互很接近會生成非常有趣的數。舉個例子， n = 22, d = 21:

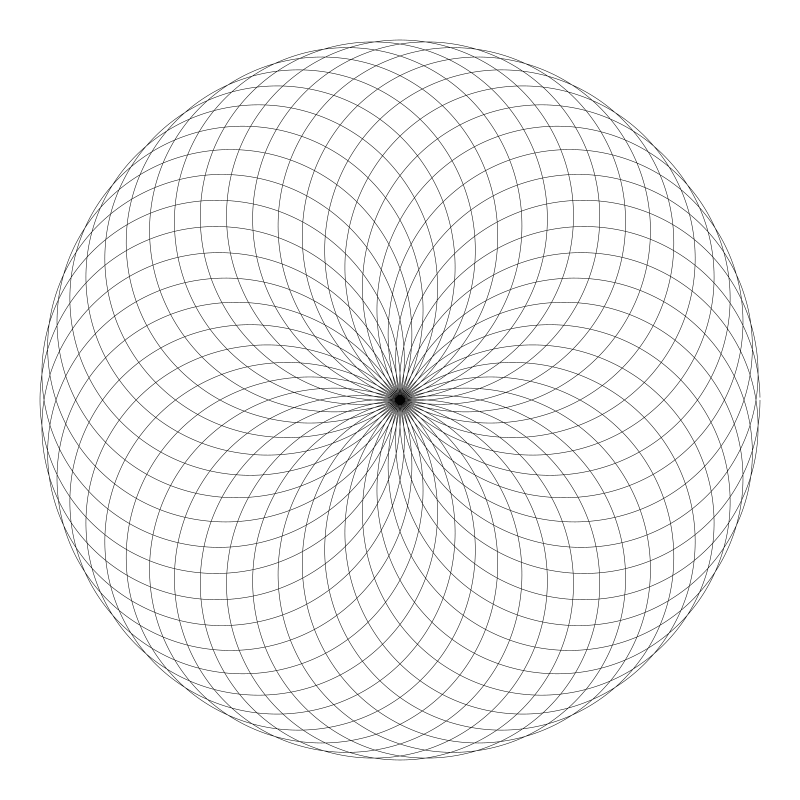
甚至是 81 和 80：

當分數小於 1.0 時圖形變得完全不同但依然很有趣。舉個例子，下圖左側圖形 n 和 d 分別為 1，2，中間圖形是 1，3， 右側圖形 1，4。

有個找到有趣圖案的小技巧是可以對的這對值可以化簡，比如 17 / 51 可以化簡成 1 / 3, 結果圖形就是上圖的中間那一幅。當改動一點點其中的某個值時，比如變成 17 / 52:

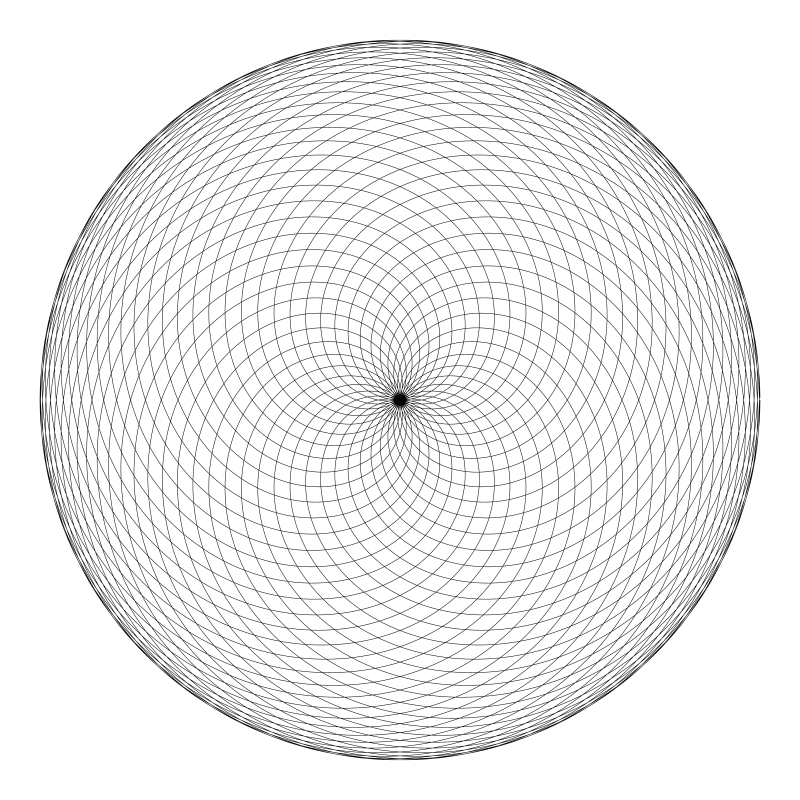
變動了 1 但造成的結果差異非常大。

有些特別的玫瑰曲線擁有自己的名稱。我分享幾個給你們。

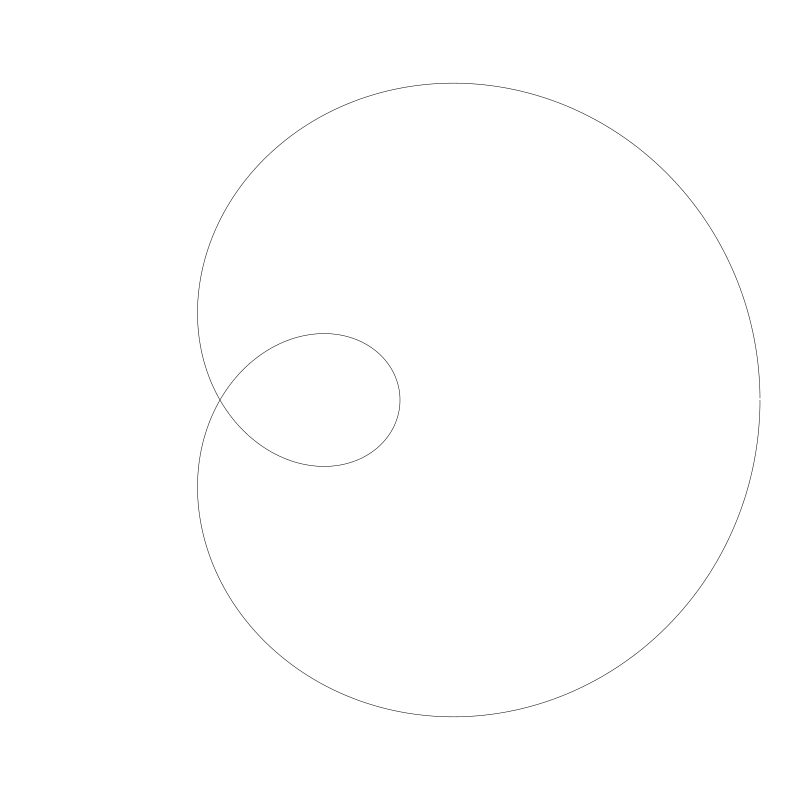
蚶線三分角 （Limaçon Trisectrix）

n / d 是 1 / 3, 我們在前面已經見過了。

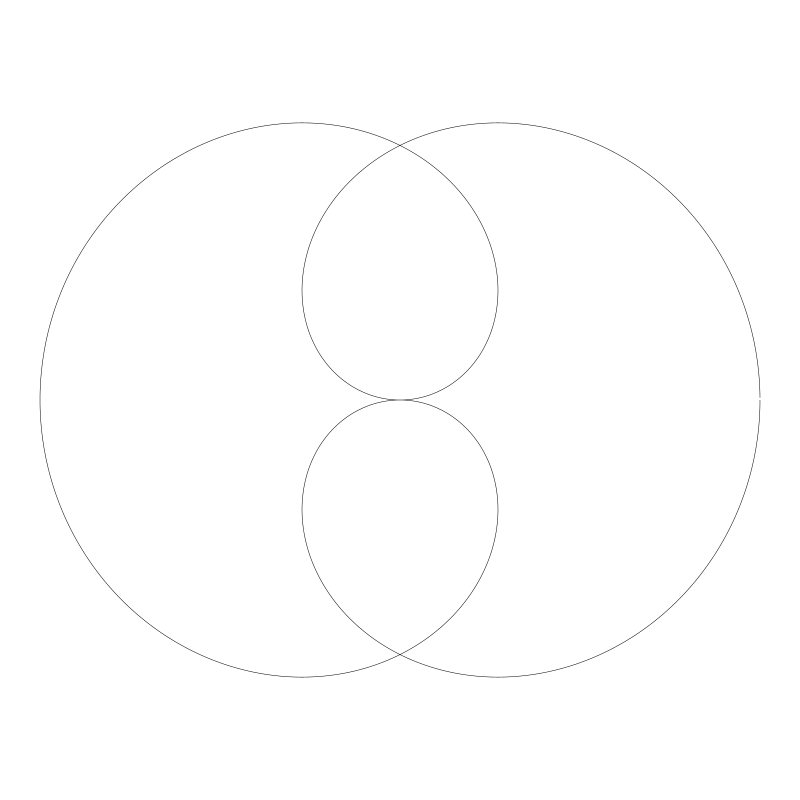
杜勒葉形線 （Dürer Folium）

n / d 是 1 / 2, 之前也見過了

四葉玫瑰線（Quadrifolium）

比例是 2 / 1

三葉玫瑰線（Quadrifolium）

比例是 3 / 1

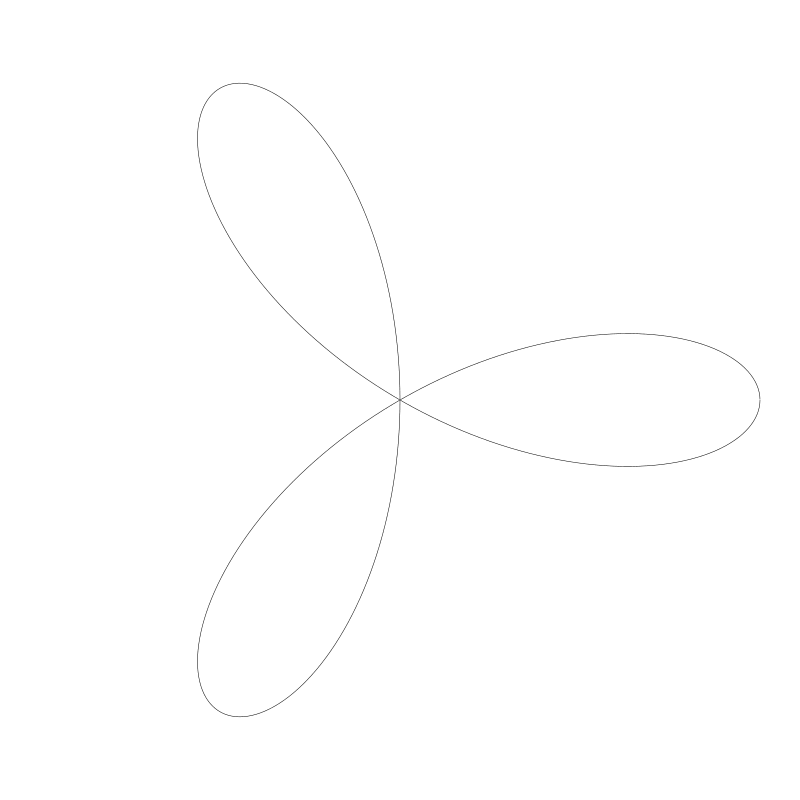
毛雷爾玫瑰（Maurer Roses）

你以為我們這就結束了？錯！還有其它型別的玫瑰形曲線等我們探索呢 -- 毛雷爾玫瑰（Maurer Roses）！

毛雷爾玫瑰 建立在 rose 函數基礎上， 與一直繪製曲線不同的是，它繪製的是一系列線段將延玫瑰曲線上的點連線起來。通常使用 360 個特殊角度的線段繪製，雖然這不是必須的。 我們先用比例為 4 / 1 建個玫瑰圖， 然後挑一個角度值用於迴圈內。此例中我使用的是 49。然後我們使用 t 迴圈 0 到 360度，將 t 乘以這個角度值。 所以 t 會從 0 遞增， 到 49, 98, 147, 196 繼續往後。我們在我們的玫瑰曲線的下一個點上應用（當然角度要轉變成弧度）。下面這個 gif 圖 表現的是前 30 次迴圈時的畫面。

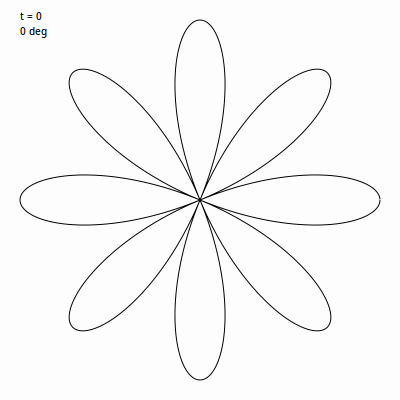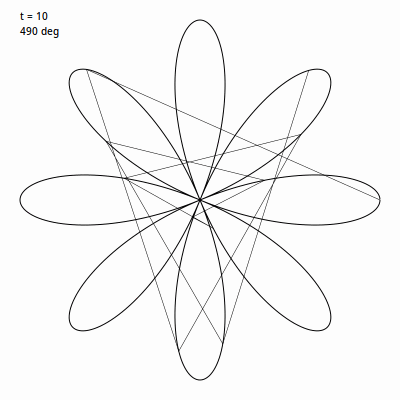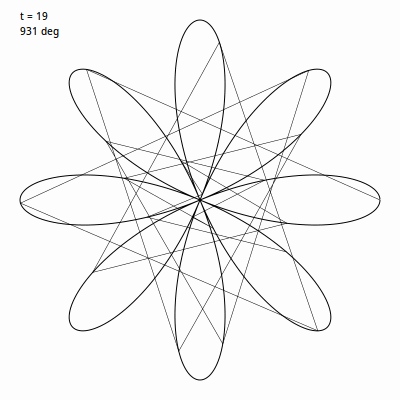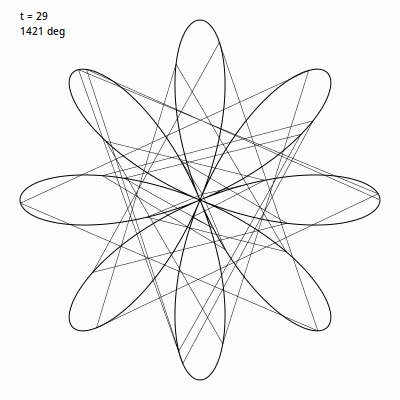
換種說法，在普通的玫瑰曲線中，遞增間隔非常非常小，所以我們可以得到一個非常平滑的曲線。這裡我們遞增間隔巨大，這會讓圖看起來亂糟糟的。但是，我們等它完成 360 次迭代路徑繪製完成，將會得到：

Aha! 全部完成後線條竟然不亂了！事實上，看起來還挺不錯。上面我在毛雷爾玫瑰上還繪製了標準玫瑰圖。但下面這個才是毛雷爾玫瑰的全貌：

我覺得兩個圖組合起來還挺好看。

所以具體怎麼做呢？

我們還是得從基礎的 rose 函數開始。 但這次，我們使用單個整數值。所以只有引數 n 沒有引數 d 了。我們還要指定每次迭代角度的遞增值。為了避免與之前 d 引數混淆，將引數名改成 deg 。這個函數簽名是：

function maurer(x, y, a, n, deg) 

還有，我們希望將 t 從 0 迴圈至 360。然後將 t 乘以 deg 。這就是角度了就像之前動畫時那樣。我們將它設為變數 k ，但在此之前還需要乘以 PI 再除以 180 轉換成弧度

function maurer(x, y, a, n, deg) {
  for (t = 0; t < 360; t++) {
    k = t * deg * PI / 180
    r = a * cos(n * k)
    lineTo(x + cos(k) * r, y + sin(k) * r)
  }
}

我們用 k 代替之前的 t 後執行 rose 演演算法。

現在我們可以像下面這樣呼叫函數了：

width = 800
height = 800
canvas(800, 800)
 
maurer(width / 2, height / 2, width * 0.45, 5, 37)
stroke()
 
// drawing the regular rose is optional
// 標準玫瑰圖可畫可不畫
rose(width / 2, height / 2, width * 0.45, 5, 1)
stroke()

得到：

對 n 和 deg 用不同的值試試。你會發現 n 的作用與前面標準玫瑰圖形一樣。但是變數 deg 即便是微小的變化都能讓圖形完全不同。 例如，在這個圖形中，n 為 7 且 deg 為 23：

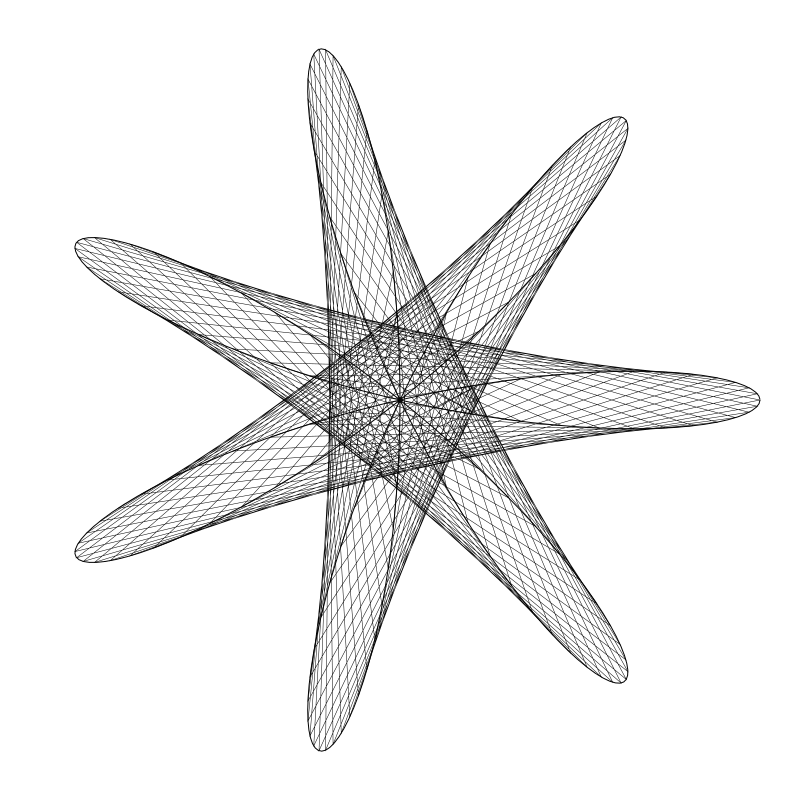
但將 deg 變為 24 時會得到下面這樣的結果：

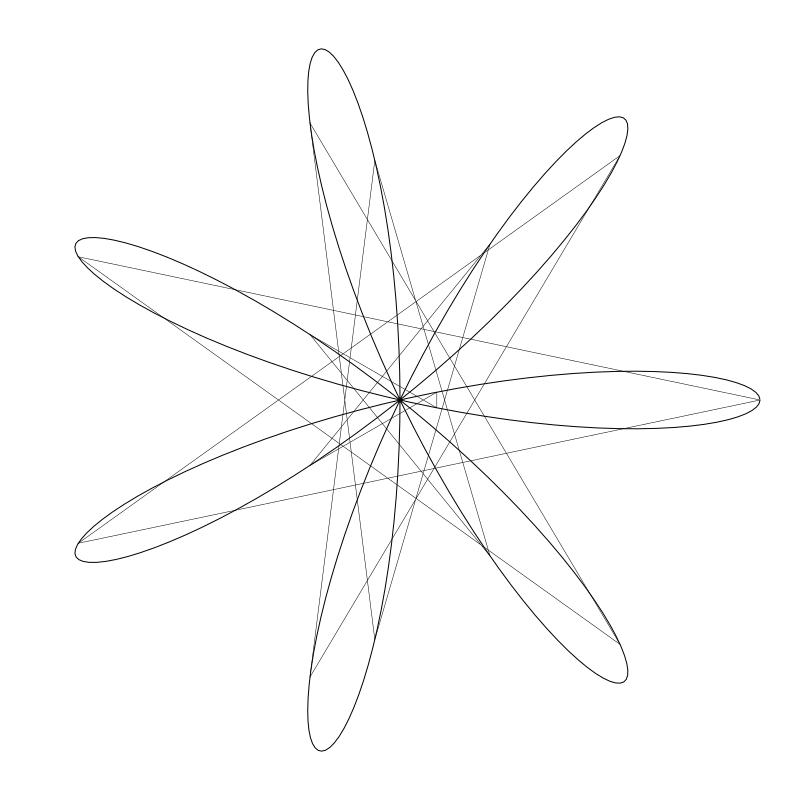
顯然沒那麼好看了。

一般來說，變數 deg 使用奇數會比偶數時要好（當然也有例外）。

任何能被 360 整除的整數都不太行。舉個例子， 4， 120：

我還是繪製了完整的圖，但毛雷爾圖形卻僅僅繪製成了右邊一個三角形。 於是將值增大到 121， 這回可就好多了：

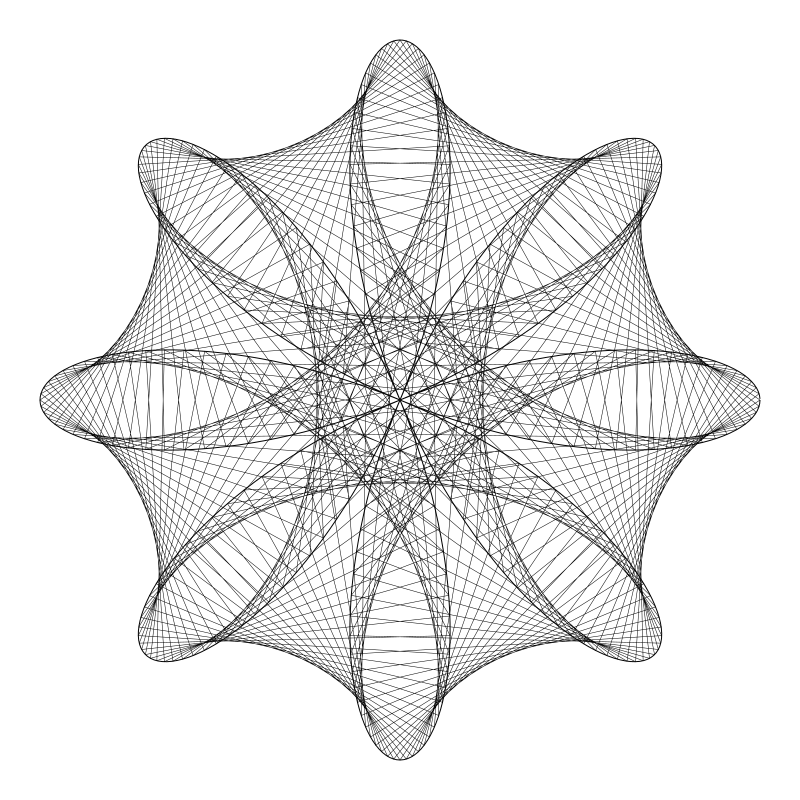
而且，較小的質數通常都都能得到較漂亮的圖形。 我注意到如果 n 值夠小那麼 deg 質數大一點兒最後的效果也還行。 我還沒有完整驗證過。我要多嘗試測試下。

還有一項你可能想嘗試的東西，就是給毛雷爾玫瑰用分數值。你完全不用改動函數。 你就直接傳一個分數值給 maurer 函數。 因為我們總是從0 迴圈至 360， 我們不需要調整迴圈範圍。下面是個傳分數值的例子，注意在給 rose 函數傳遞時兩個引數還是分開傳的。

maurer(0, 0, width * 0.45, 5.0 / 4.0, 229)
stroke()
rose(0, 0, width * 0.45, 5, 4)
stroke()

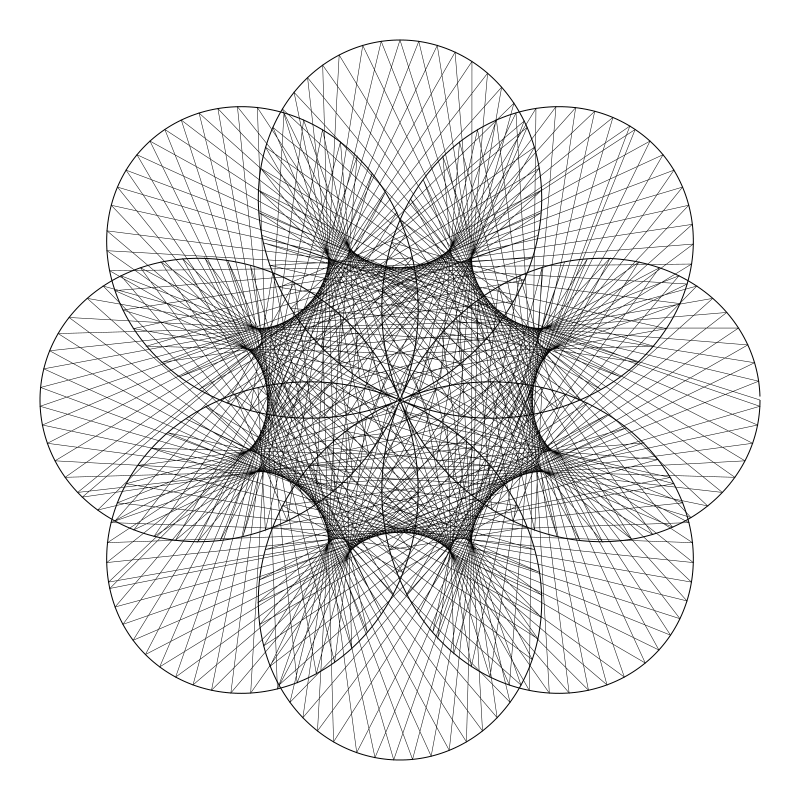
看看你能在所有可能的圖形變化中找到什麼。

本章 Javascript 原始碼 https://github.com/willian12345/coding-curves/blob/main/examples/ch11

---

部落格園: http://cnblogs.com/willian/
github: https://github.com/willian12345/