技術文章 » 解密Prompt系列9. 模型複雜推理-思維鏈COT基礎和進階玩法

解密Prompt系列9. 模型複雜推理-思維鏈COT基礎和進階玩法

2023-06-16 09:00:50

終於寫了一篇和系列標題沾邊的部落格，這一篇真的是解密prompt！我們會討論下思維鏈(chain-of-Thought)提示詞究竟要如何寫，如何寫的更高階。COT其實是Self-ASK，ReACT等利用大模型進行工具呼叫方案的底層邏輯，因此在Agent呼叫章節之前我們會有兩章來講思維鏈

先打預防針，COT當前的研究多少存在一些玄學成分，部分COT的研究使用的模型並非SOTA模型，以及相同的COT模板在不同模型之間可能不具備遷移性，且COT的效果和模型本身能力強相關，哈哈可以去圍觀COT小王子和Claude友商的Prompt決戰]。本章只是為大家提供一些思維鏈設計的思路，以及給Agent呼叫做一些鋪墊。

思維鏈的核心是為了提高模型解決複雜推理問題的能力，包括但不限於符號推理，數學問題，決策規劃等等，Chain-of-Thought讓模型在得到結果前，模擬人類思考推理的過程生成中間的推理步驟。適用於以下場景

  • 有挑戰的任務
  • 解決任務本身需要多步推理
  • 模型規模對任務效果的提升相對有限

COT基礎用法

Few-shot COT

Chain of Thought Prompting Elicits Reasoning in Large Language Models

開篇自然是COT小王子的成名作，也是COT的開山之作，單看參照量已經是一騎絕塵。

論文的核心是通過Few-shot的方案，來引導模型生成中間推理過程，並最終提高模型解決複雜問題的能力。核心邏輯很Simple&Naive

  • 通過在Few-shot樣本中加入推理過程，可以引導模型在解碼過程中，先給出推理過程，再得到最終答案
  • 類似中間推理過程的加入，可以顯著提高模型在常識推理，數學問題，符號推理等複雜推理問題上的模型表現。

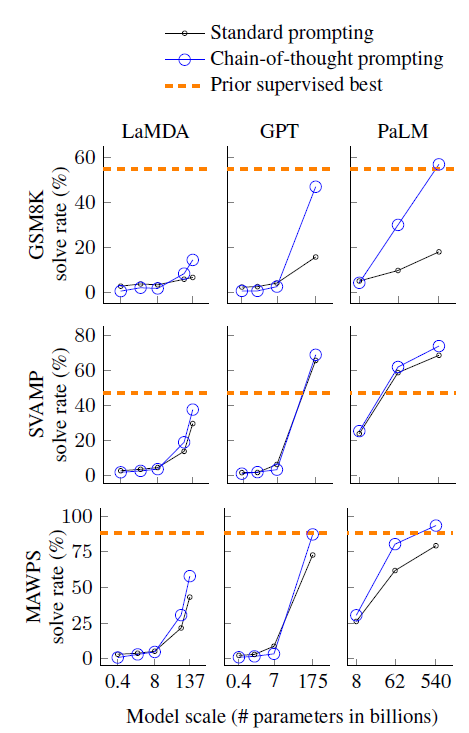
先看效果，見上圖，可以得到幾個insights

  • COT帶來的效果提升具有湧現性，只在100B左右的大模型上才出現顯著更優的效果，但作者沒有給出模型規模的影響原因
  • COT帶來的效果提升在複雜問題例如GSM8K上表現更顯著

讓我們直觀來看下COT的Few-shot模板構建，以及對解碼的影響。這裡我們使用Belle的數學COT指令樣本取樣10個構建了一組few-shot思維鏈指令，如下，

測試數學能力嘛，小學奧數經典的汽車相遇問題走一個，問題：兩輛汽車從相距500千米的兩城同時出發，相向而行．一輛摩托車以每小時80千米的速度在兩輛汽車之間不斷往返聯絡．已知這兩輛汽車的速度分別是每小時40千米和60千米，求兩汽車相遇時，摩托車共行駛了多少千米？題目不復雜500/(40+60)*80 = 400千米

以下分別使用ChatGPT和ChatGLM在Greedy-search模式下進行解碼，分別是直接提問和加入few-shot-cot後再提問

prompt chatgpt chatglm-6b
直接提問 設兩汽車相遇時間為\(t\)小時，則兩汽車相遇時的距離為\((40+60)t=100t\)千米。摩托車在這\(t\)小時內不斷往返，相當於在兩汽車之間來回行駛了\(2\times 80t=160t\)千米。因此，摩托車共行駛了\(160t\)千米。根據題意，兩汽車相遇時的距離為500千米，因此\(t=\frac{500}{100}=5\)小時。代入可得，摩托車共行駛了\(160\times 5=\boxed{800}\)千米。 設兩汽車相遇時，摩托車行駛了 \(x\) 小時。根據題意，兩汽車相向而行，它們的相對速度為 \(40+60=100\) 千米/小時。因此，兩汽車相遇時，它們行駛的距離之和為：\(500\times(100+40)=50000\)因為兩汽車相遇時，摩托車一直在行駛，所以摩托車行駛的距離等於兩汽車相遇時它們行駛的距離之和：\(x\times80=50000\)解得：\(x=4000\)因此，兩汽車相遇時，摩托車共行駛了 \(4000\) 千米。
few-shot COT 設摩托車共行駛了x千米，則兩輛汽車相遇時，摩托車往返的次數為x/500。在每次往返中，摩托車行駛的距離為80千米，所以摩托車共行駛的距離為：x = (80千米) × (x/500) = 0.16x千米兩輛汽車相遇時，它們的總路程為500千米，所以它們相遇所用的時間為：t = 500千米 / (40千米/小時 + 60千米/小時) = 5小時根據摩托車的速度和時間，可以得到：x = 80千米/小時 × 5小時 = 400千米因此，摩托車共行駛了400千米。 設兩汽車相遇時，摩托車行駛了 \(x\) 小時。由題意可知，兩汽車相遇時，它們已經行駛了 500 千米，所以有：\(40x + 60x = 500\)解得 \(x=50/9\)，即兩汽車相時，摩托車行駛了 50/9 小時。因此，摩托車共行駛了：\(80 \times (50/9) = 400\)

加入COT之後chatgpt和chatglm都雙雙答對了，雖然有運氣成分，且推理過程還顯得有點智障吧。但你會發現不加入few-shot COT模型同樣會進行推理再給出答案，而非像論文中給出的模型會直接直接給一個答案沒有任何推理。原因是論文使用的是text-davinci-002是沒有經過RLHF的舊版本模型。我們在一些需要推理的多項選擇問題上也進行了測試，不管是使用few-shot COT還是加入COT指令樣本進行微調，確實都能帶來一定程度上推理/數學能力的提升。

論文還進行了一些消融實驗包括

  • 準確率提升是否來自數學公式的引入？

論文嘗試了few-shot部分只加入公式並不能顯著提升效果。個人感覺這個消融實驗不太完整，因為很多複雜MWP問題模型很難對映到單一的公式，而先進行問題分解後再逐步對映到中間公式，在我們的場景裡是可以提升效果的。這裡推薦兩個資料集：APE210K和Math23K分別是猿輔導和騰訊開源的數學世界問題轉化成公式的資料集，大家可以自己試試看

  • 準確率提升是否因為few-shot-cot幫助模型更好的召回相應的知識？

論文嘗試了先給出答案再進行推理的prompt模板，發現效果顯著變差。說明few-shot-COT只是啟用模型給出推理，推理過程本身才是模型效果提升的核心。我們在一些需要推理的多項選擇問題上也發現，先推理再回答選項的效果顯著優於先回答選項再給出推理過程

zero-shot COT

Large Language Models are Zero-Shot Reasoners

除了使用Few-shot-COT樣本可以讓模型給出推理過程，單純用指令也可以讓模型給出思維鏈，且能進一步提升模型複雜問題推理能力。論文中效果最好的啟用思維鏈的指令是"Let's think step by step"哈哈哈，我當時論文看到這裡感覺空氣都凝固了

self-consistency的基礎假設很人性化：同一個問題不同人也會給出不同的解法，但正確的解法們會殊途同歸得到相同的正確答案。以此類比模型解碼，同一問題不同隨機解碼會得到不同的思維鏈推理過程，期望概率最高的答案，準確率最高。那核心就變成針對多個解碼輸出，如何對答案進行聚合。論文對比了以下幾種方案

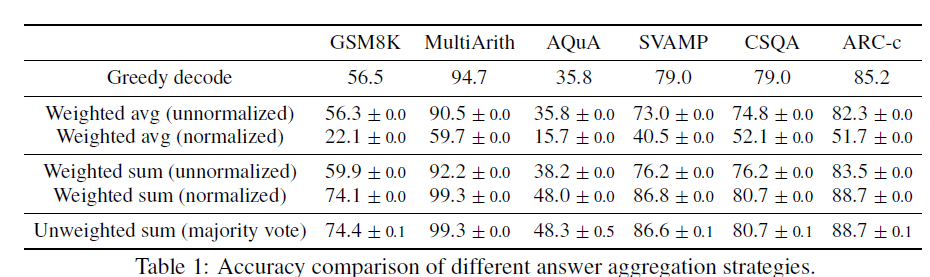
給定指令prompt和問題question，模型通過隨機解碼會生成一組\(a_1,a_2,...a_m\)答案候選，以及對應的思維鏈路徑\(r_1,r_2,...r_m\)。效果最好的兩種聚合方案分別是

  1. major vote：直接對解碼後的結果投票大法投出一個出現概率最高的答案。該說不說大道至簡，最簡單的方案往往是最好的, 論文後面的結果都是基於投票法給出的
  2. normalized weighted sum: 計算\((r_i, a_i)\)路徑的概率,既模型輸出的每一個token條件解碼概率求和，並對解碼長度K進行歸一化。雖然這裡略讓人驚訝，本以為加權結果應該會更好，可能一定程度也說明模型的解碼概率在答案的正確性上其實不太有區分度。

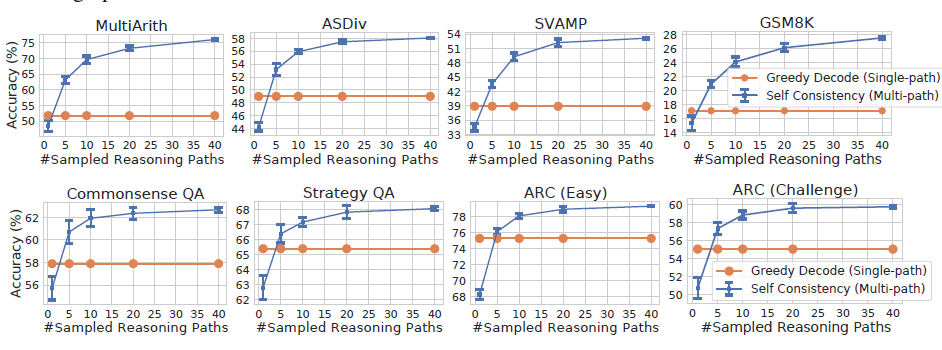
\[p(r_i,a_i|prompt, question)=exp(\frac{1}{k}\sum_{k=1}^K logP(t_k|prompt,question,t_1,...t_{k-1})) \]

針對解碼引數論文還做了一些測試

  1. 隨機引數：self-consistency支援不同的隨機解碼策略，在引數設定上需要平衡解碼的多樣性和準確率，例如temperature太低會導致解碼差異太小，投票投了個寂寞，太高又會影響最終的準確率。看測試可能top-p=40, temperature=0.5是一個不錯的測試起點

  1. 取樣次數：major vote的效果很依賴候選樣本數，論文中很豪橫取樣了40次，地主家的兒子也不敢這麼玩...看效果取樣5次以上就能超過Greedy解碼，具體解碼次數看你家有多少餘糧吧...

Least-to-Most

LEAST-TO-MOST PROMPTING ENABLES COMPLEX REASONING IN LARGE LANGUAGE MODELS

如果說上面的Self-Consisty多少有點暴力出奇跡，那Least-to-Most明顯更優雅一些。思路很簡單，在解決複雜問題時，第一步先引導模型把問題拆分成子問題；第二步逐一回答子問題，並把子問題的回答作為下一個問題回答的上文，直到給出最終答案，主打一個循序漸進的解決問題。也可以理解為通過few-shot來引導模型給出更合理，更一致的推理思路，再根據這個思路在解決問題。

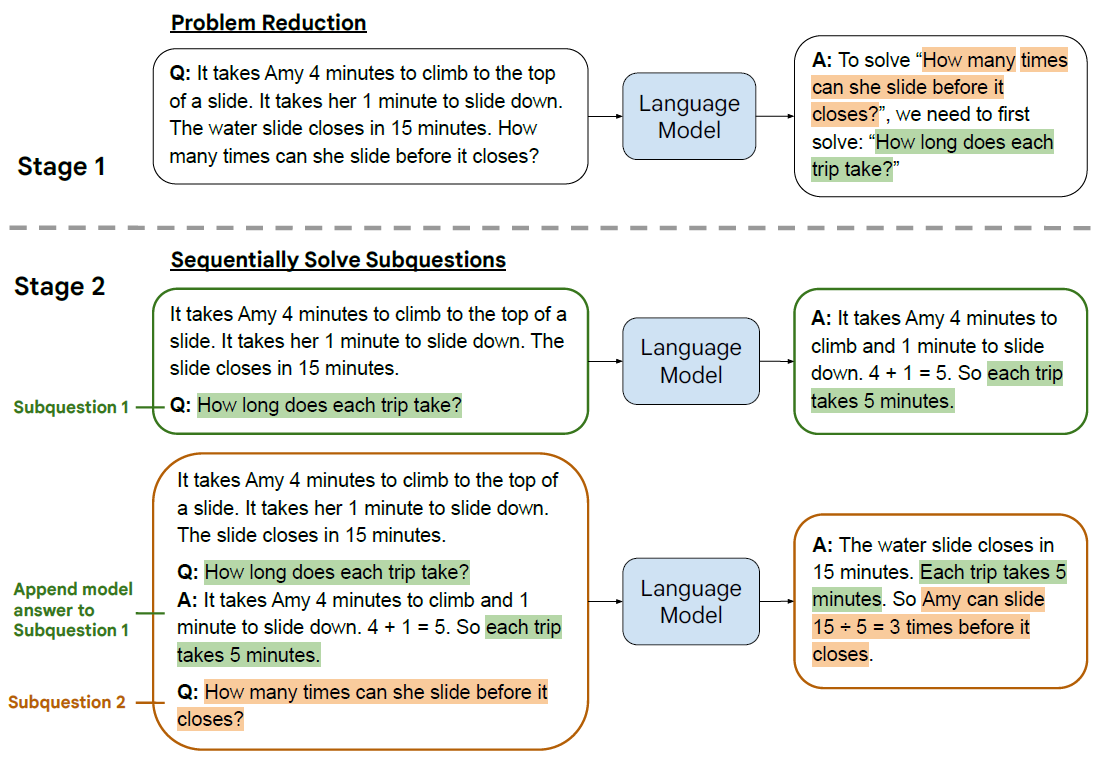
設計理念很好，但我最好奇的是few-shot-COT要如何寫，才能引導模型針對不同場景進行合理的問題拆解。這裡我們還是看下針對數學問題的few-shot應該如何構建的，論文中的few-shot-prompt是純手工寫製作，這裡我採用chatgpt來生成再人工調整。從APE21K中隨便抽了3個問題，注意不要太簡單，已經有論文證明，few-shot-COT樣本的推理步驟越多效果越好。這裡我拆解問題的Prompt(未調優)是"對以下數學問題進行問題拆解，分成幾個必須的中間解題步驟並給出對應問題, 問題："，來讓ChatGPT生成中間的解題步驟作為few-shot-cot模板

  1. Problem Reducing 問題拆解

還是同一道相遇問題，通過Reduce prompt，ChatGPT輸出：要解答摩托車共行駛了多少千米？我們需要回答以下問題:"兩輛汽車相遇需要多長時間？"，"摩托車在這段時間內共行駛了多少千米？

以上的問題拆解不是非常穩定，有時會包括最終的問題，有時只包括中間的解題步驟，為了保險起見，你可以在解析的問題後面都再加一個原始的問題。

  1. Sequentially Solve 子問題有序回答

把Reduce步驟的子問題解析出來，按順序輸入chatgpt，先回答第一個子問題

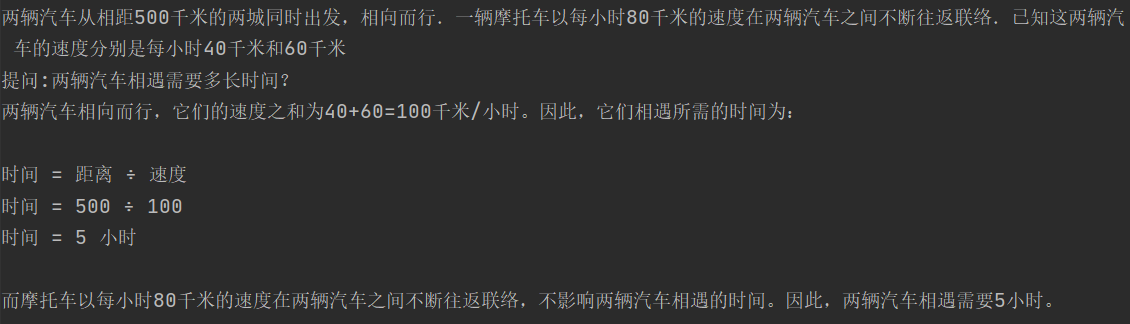
再把第一個子問題和回答一起拼接作為上文，這裡使用對話history也可以，拼接只是為了直觀展示

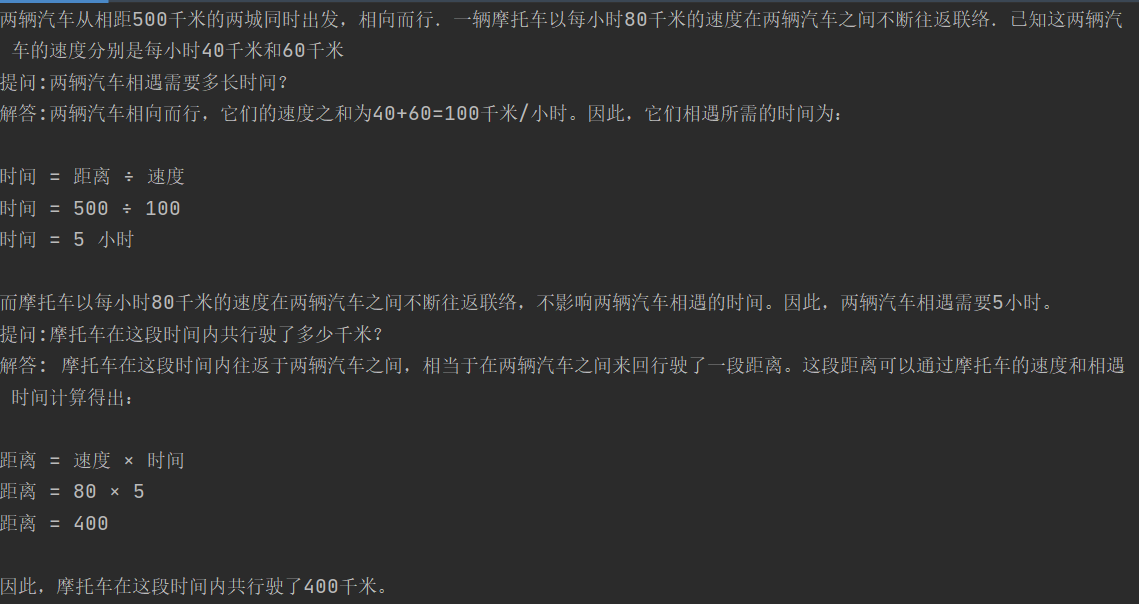
Least-to-Most最值得借鑑的還是它問題拆分的思路，這在後面被廣泛借鑑，例如Agent呼叫如何拆分每一步的呼叫步驟，以及如何先思考再生成下一步Action，在這些方案裡都能看到Least-to-Most的影子。

想看更全的大模型相關論文梳理·微調及預訓練資料和框架·AIGC應用，移步Github >> DecryptPropmt