前言

遺傳演演算法是一種模擬自然進化過程與機制來搜尋最優解的方法，它由美國 John Holland 教授於20世紀70年代提出。遺傳演演算法的主要思想來源於達爾文生物進化論和孟德爾的群體遺傳學說，通過數學的方式，將優化問題轉換為類似生物進化中的染色體基因的交叉和變異等過程，因此具有堅實的生物學基礎和鮮明的認知學意義。和許多傳統優化演演算法尤其是基於梯度的演演算法相比，遺傳演演算法通過交叉和變異引入的隨機性減少了陷入區域性最優解的概率。同時遺傳演演算法以適應度函數為導向，無需計算目標函數的導數和其他資訊，這使得它適用於複雜的非線性和多維優化問題，因此被廣泛應用於圖形識別、影象處理、自動控制、工程設計和機器人等領域，具有廣泛的應用價值。

雖然遺傳演演算法表現優異，但是它的各個引數對其效能有著重要的影響。對於一個優化問題，如果沒有找到合適的遺傳演演算法引數，可能導致演演算法早熟或者收斂效能差的問題，需要迭代多個世代才能找到全域性最優解。這些問題毫無疑問會阻礙遺傳演演算法的落地應用，因此研究各個引數對演演算法產生了怎樣的影響，進而確定合適的引數選取準則，對於改善遺傳演演算法的搜尋能力和收斂速度有著重要的意義。

本文通過遺傳演演算法求解 Rastrigin 函數在二維空間的最小值問題，研究演演算法的各個引數的變化對最優解和收斂速度的影響，進而給出遺傳演演算法引數選取準則，使得遺傳演演算法在具體問題上能有更優異的表現。

遺傳演演算法

遺傳演演算法將優化問題的可行解編碼為二進位制形式，稱為染色體。對於多維空間下的可行解，每個維度被編碼為二進位制形式的基因，共同組成了一條染色體。

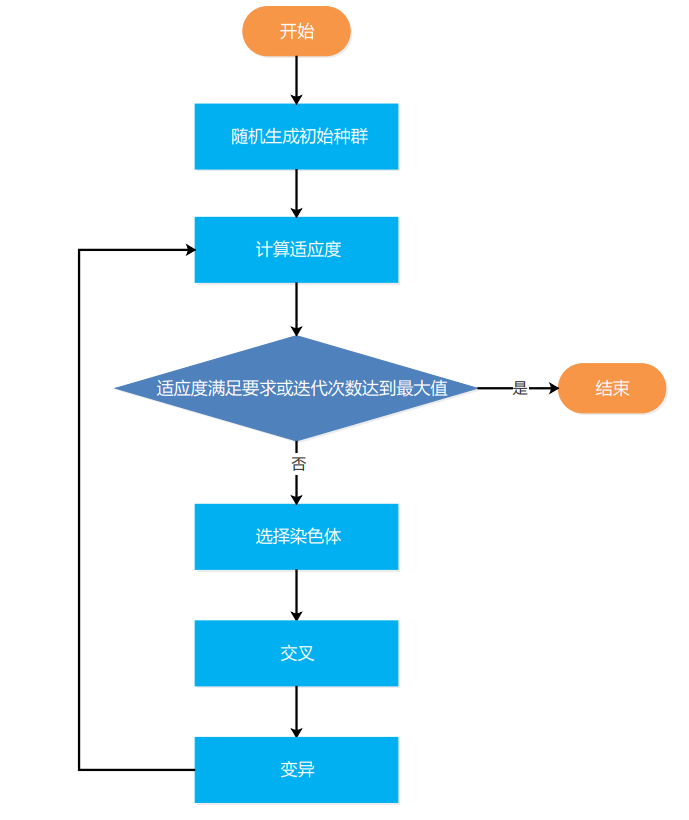
遺傳演演算法的流程如下圖所示，可以分為以下幾個過程：

初始化種群。在種群個體數為 \(N\) 和基因長度為 \(L_c\) 的情況下，隨機生成 \(N\) 條染色體，作為初始種群 \(X_0\)。
個體評價。使用適應度函數計算種群中各條染色體 \(C_i\) 的適應度 \(f_i\)。
終止條件判斷。如果適應度變化幅度小於指定的閾值或者迭代次數達到最大值，結束遺傳演演算法，將種群中適應度值最大的染色體解碼，可以得到最優解；否則繼續下一步。
選擇。根據各條染色體適應度的值，計算染色體的選擇概率 \(f_i=f_i / ∑f_i\)，使用輪盤賭演演算法隨機選擇出 \(M=(1-α)N\) 條染色體，其中 \(α\) 代表保留的適應度值最大的染色體的比例，這部分保留的染色體不會參與下面的交叉和變異過程，而是作為優秀個體被保留到下一次迭代。
交叉。對輪盤賭演演算法選出的 \(M\) 條染色體中的每一條染色體 \(C_f\)，在交叉概率為 \(P_c\) 的情況下隨機選擇另一條染色體 \(C_m\) 和一個交叉位置 \(k\)，將 \(C_f [0:k-1]\) 和 \(C_m[k:]\) 進行拼接，生成新染色體 \(C_c\)。
變異。對 \(M\) 條染色體分別獨立依概率 \(P_m\) 進行一個隨機位元的翻轉。
回到步驟 2 計算新種群的個體適應度。

可以看到，遺傳演演算法的上述流程中共有6個引數需要調節，各個引數如下表所示：

符號	說明
\(N\)	種群規模，即種群染色體的數量
\(L_c\)	基因長度
\(\alpha\)	保留的優秀染色體比例
\(P_c\)	交叉概率
\(P_m\)	變異概率
\(\varepsilon\)	適應度變化閾值或迭代次數

程式碼實現

使用 Python 實現的遺傳演演算法如下所示，使用 get_solution() 方法可以對目標函數求極值：

class GA:
    """ 遺傳演演算法 """

    def __init__(self, pop_size=200, dna_size=20, top_rate=0.2, crossover_rate=0.8, mutation_rate=0.01, n_iters=100):
        """
        Parameters
        ----------
        pop_size: int
            種群大小

        dna_size: int
            染色體大小

        top_rate: float
            保留的優秀染色體個數

        crossover_rate: float
            交叉概率

        mutation_rate: float
            變異概率

        n_iters: int
            迭代次數
        """
        self.pop_size = pop_size
        self.dna_size = dna_size
        self.top_rate = top_rate
        self.crossover_rate = crossover_rate
        self.mutation_rate = mutation_rate
        self.n_iters = n_iters

    def get_solution(self, obj_func, bound: List[tuple], is_min=True):
        """ 獲取最優解

        Paramters
        ---------
        obj_func: callable
            n 元目標函數

        bound: List[tuple]
            維度為 `(n, 2)` 的取值範圍矩陣

        is_min: bool
            尋找的是否為最小值

        Returns
        -------
        index: int
            最優解的下標

        Xm: list
            歷次迭代的最優解

        Ym: list
            歷次迭代的最優值
        """
        Xm, Ym = [0], [0]

        # 初始化種群
        pop = np.random.randint(
            2, size=(self.pop_size, self.dna_size*len(bound)))
        Xm[0], Ym[0] = self._get_best(pop, obj_func, bound, is_min)

        # 迭代求最優解
        for _ in range(self.n_iters):
            X = self._decode(pop, bound)
            fitness = self._fitness(obj_func, X, is_min)
            keep, selected = self._select(pop, fitness)
            new = self._crossover_mutation(selected)
            pop = np.vstack((keep, new))

            xm, ym = self._get_best(pop, obj_func, bound, is_min)
            Xm.append(xm)
            Ym.append(ym)

        idx = np.argmin(Ym) if is_min else np.argmax(Ym)
        return idx, Xm, Ym

    def _decode(self, pop: np.ndarray, bound: List[tuple]):
        """ 將二進位制數解碼為十進位制數 """
        result = []
        N = 2**self.dna_size-1
        pows = 2**np.arange(self.dna_size, dtype=float)[::-1]
        for i, (low, high) in enumerate(bound):
            X = pop[:, i*self.dna_size:(i+1)*self.dna_size]
            X = low + (high-low)*X.dot(pows)/N
            result.append(X)

        return result

    def _fitness(self, obj_func, X: tuple, is_min=True):
        """ 適應度函數 """
        y = obj_func(*X)
        e = 1e-3
        return -y+np.max(y)+e if is_min else y-np.min(y)+e

    def _select(self, pop: np.ndarray, fitness: np.ndarray):
        """ 根據使用度選擇染色體 """
        # 保留一定比例的優秀染色體
        n_keep = int(self.pop_size*self.top_rate)
        idx_keep = (-fitness).argsort()[:n_keep]

        # 按照適應度值隨機挑選出剩下的染色體
        n_select = self.pop_size-n_keep
        p = fitness/fitness.sum()
        idx = np.random.choice(np.arange(self.pop_size), n_select, True, p)

        return pop[idx_keep], pop[idx]

    def _crossover_mutation(self, pop: np.ndarray):
        """ 交叉變異 """
        result = []
        for child in pop:
            # 交叉
            if np.random.rand() < self.crossover_rate:
                mother = pop[np.random.randint(len(pop))]
                point = np.random.randint(pop.shape[1])
                child[point:] = mother[point:]

            # 變異
            if np.random.rand() < self.mutation_rate:
                pos = np.random.randint(pop.shape[1])
                child[pos] = 1 - child[pos]

            result.append(child)

        return np.array(result)

    def _get_best(self, pop: np.ndarray, obj_func, bound: List[tuple], is_min):
        """ 獲取最優解及其目標函數值 """
        X = self._decode(pop, bound)
        Y = obj_func(*X)
        idx = np.argmin(Y) if is_min else np.argmax(Y)
        xm = [x[idx] for x in X]
        return xm, Y[idx]
    
def f(x, y):
    """ 目標函數 """
    return 20+x*x+y*y-10*(np.cos(2*np.pi*x)+np.cos(2*np.pi*y))


if __name__ == '__main__':
    ga = GA(dna_size=50)

    idx, Xm, Ym = ga.get_solution(f, [(-5, 5), (-5, 5)])
    print("最優解：", Xm[idx], "目標函數值：", Ym[idx])

    plt.plot(np.arange(ga.n_iters+1), Ym)
    plt.show()

實驗

本文使用遺傳演演算法求取 Rastrigin 函數在二維空間的最小值問題，優化問題可描述為：

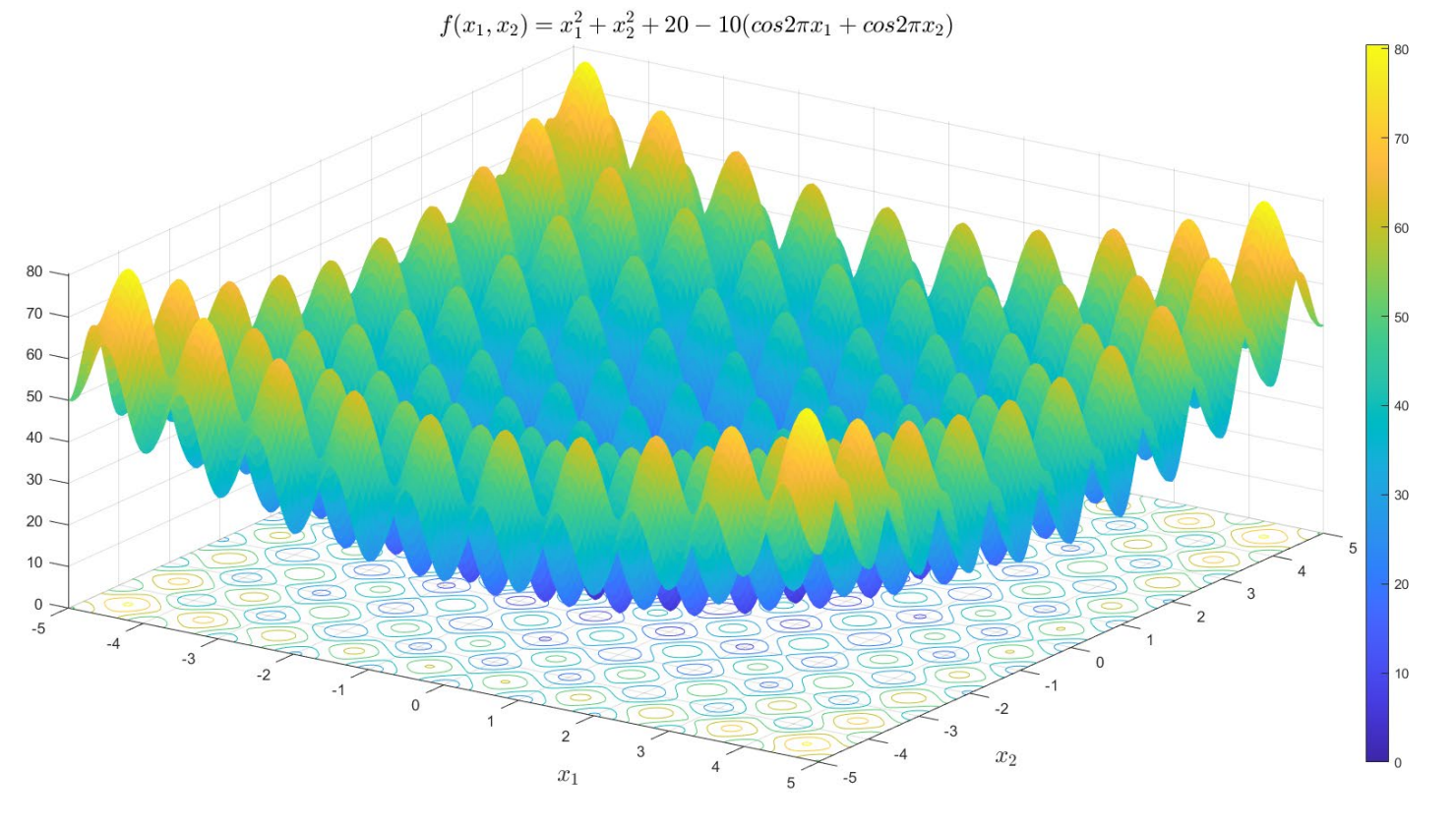
\[\min f(x_1, x_2)=20+x_1^2+x_2^2-10(cos2\pi x_1+cos2\pi x_2),\ s.t.-5\le x_1,x_2 \le 5 \]

觀察函數影象可知 Rastrigin 函數具有多個區域性最小值點，在 \((0,0)\) 處是最優全域性最優解，此時最優目標值為 \(f^*(x_1, x_2)=0\)。為了更好地研究各個引數的變化對遺傳演演算法的搜尋能力和收斂速度的影響，本文在 \(N=200,\ L_c=20,\ \alpha=0.2,\ P_c=0.8,\ P_m=0.01,\ \varepsilon=100\)（使用迭代次數作為結束條件）的條件下分別調整每個引數，模擬並分析每個引數值下目標函數值曲線的變化。為了減少隨機性造成的干擾，每個引數下進行 10 次模擬，並取平均值作為最終結果。

調整種群規模

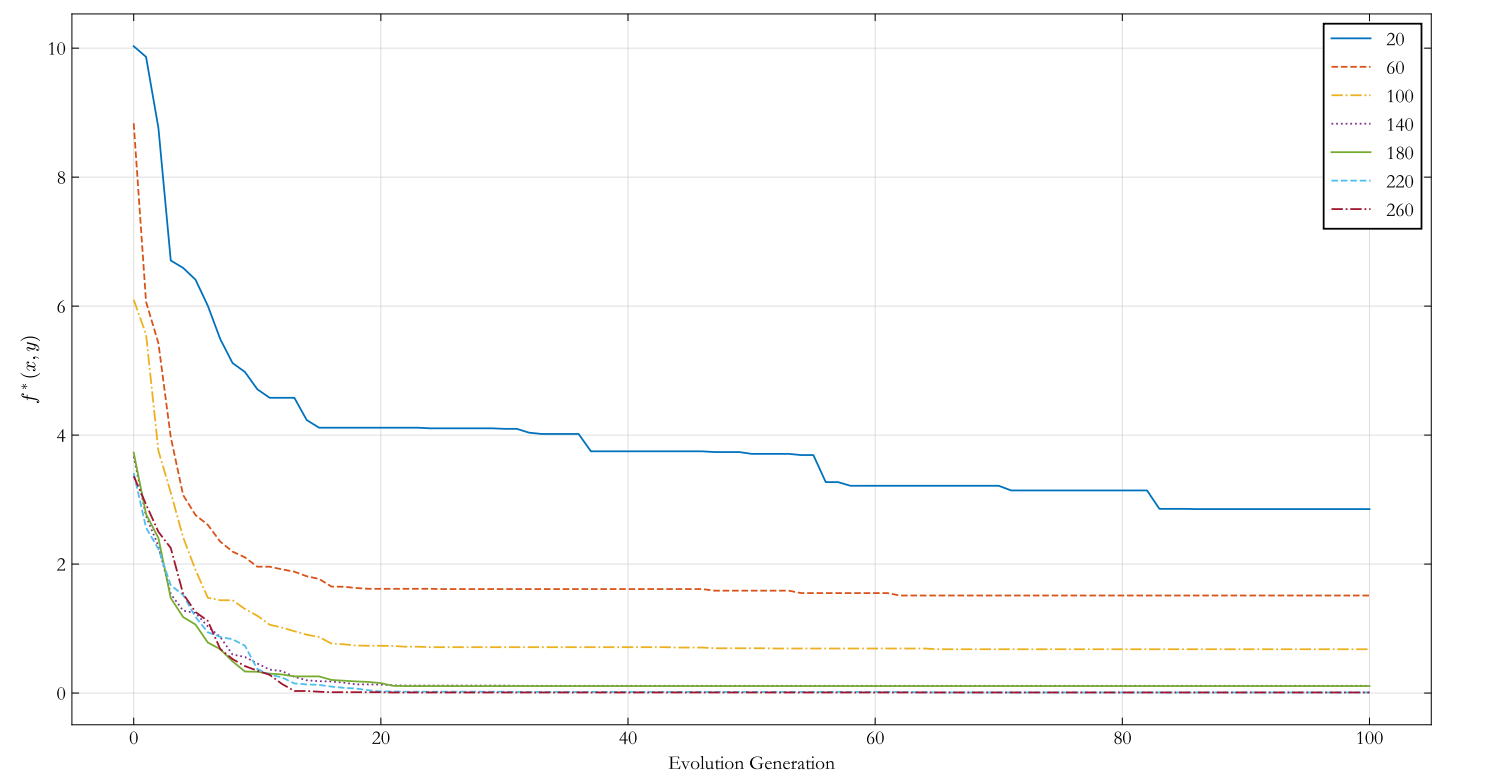
當種群規模在 \([20, 260]\) 區間內變化時，迭代曲線如下圖所示。可以看到，當種群規模較小時，種群多樣性會比較少，會造成近親繁殖的現象，演演算法容易陷入區域性最優解且收斂速度較慢。隨著種群規模的擴大，多樣性逐漸提升，交叉和變異更有可能繁殖出更優秀的個體，演演算法很快就收斂於全域性最優解。對比 \(N=180\) 和 \(N=260\) 的迭代曲線，發現二者的收斂速度差異並不大，所以種群數量不能設定過大，一味增大種群數量只會造成運算開銷的上升。

調整基因長度

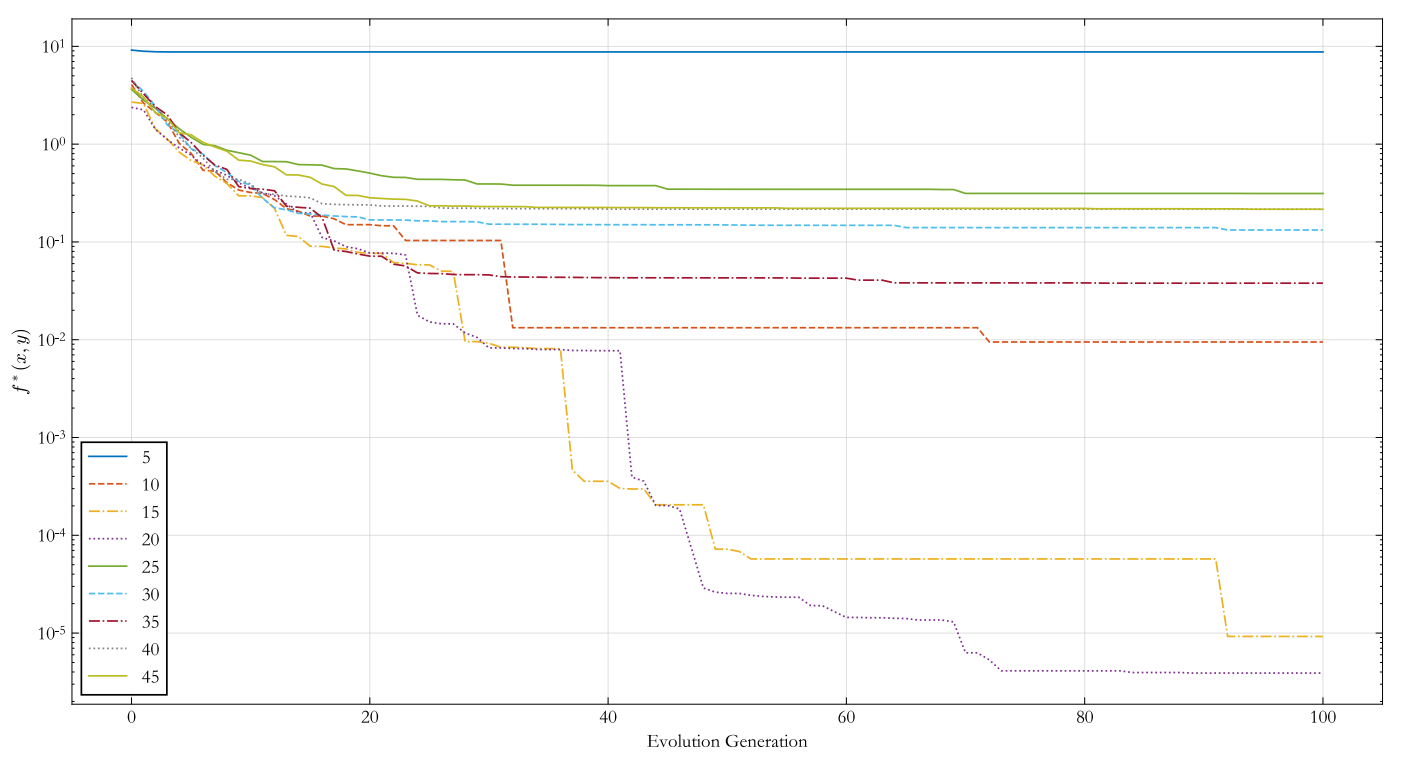
基因長度對迭代曲線的影響如下圖所示，由圖可知，當基因長度為 \(L_c=5\) 時，二進位制資料解析度過低，演演算法很快收斂到解 \((1.129, 1.129)\)。有趣的是當基因長度 \(L_c \in \{ 35,40,45 \}\) 時的收斂到最優解的速度並沒有快於 \(L_c=20\) ，原因在於染色體長度越大，解析度就越高，這減小了隨機交叉和變異對染色體的十進位制數的影響。

調整保留的最優染色體比率

保留最優染色體的比率在 \([0.1, 0.9]\) 之間變化時，迭代曲線的對比如下圖所示。由圖可知，如果保留的最優染色體過多，會導致用於交叉和變異的染色體數量變少，減少了演演算法從區域性最優解跳到全域性最優解的可能性，因此 \(\alpha = 0.9\) 時演演算法收斂速度明顯慢於其他曲線。而 \(\alpha = 0.1\) 時保留的最優個體太少，過多的交叉和變異可能導致演演算法在多個區域性最優解之間跳動，只有 \(\alpha \in \{0.2, 0.3, 0.4\}\) 時演演算法快速地收斂於全域性最優解。

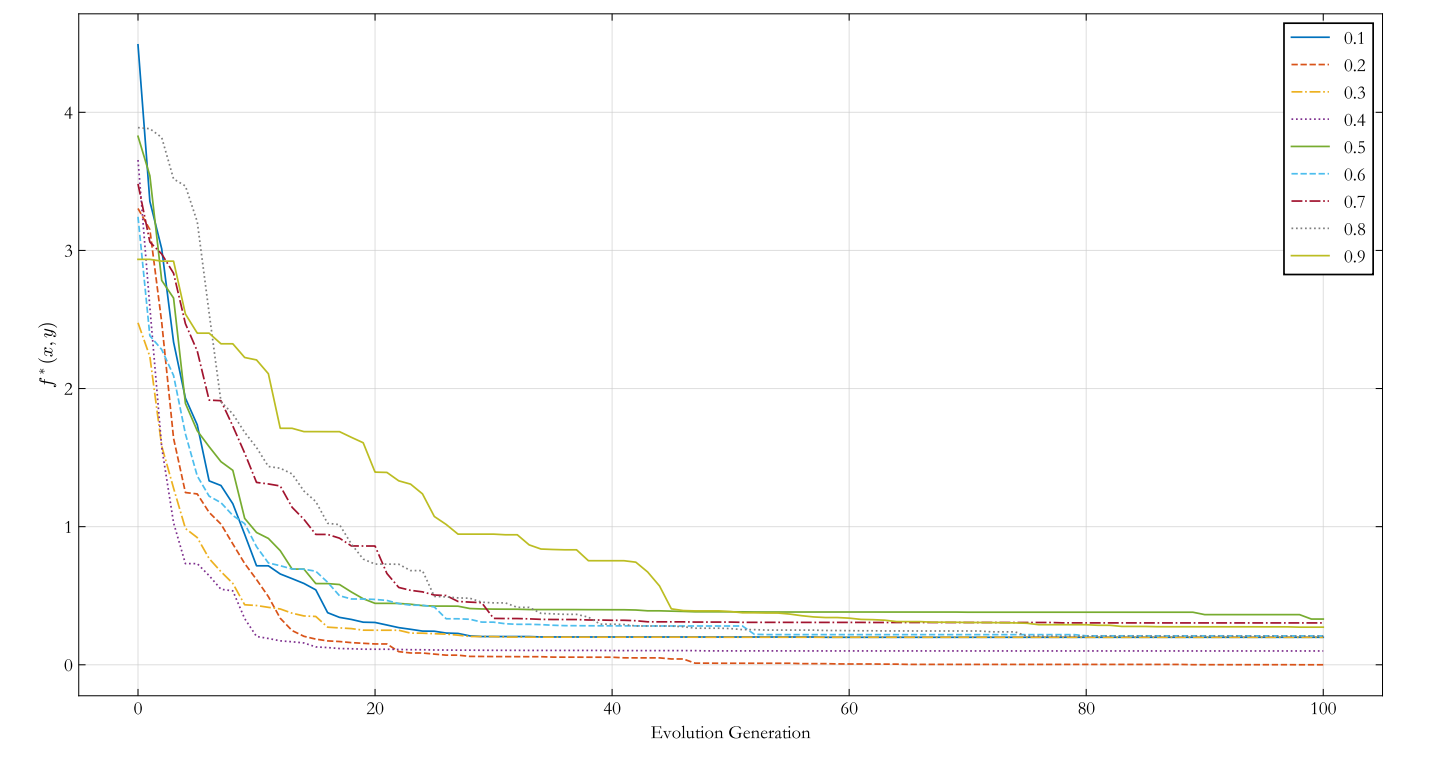
調整交叉概率

交叉概率在 \([0.1, 1.0]\) 之間變化時，迭代曲線的對比如下圖所示。可以發現，交叉概率較小時，種群內的染色體通過交叉繁衍出更優秀個體的概率也更低，因此演演算法收斂速度較慢。而交叉概率取 0.8 以上的值時，種群繁衍出優秀個體的概率變大，收斂速度明顯加快。

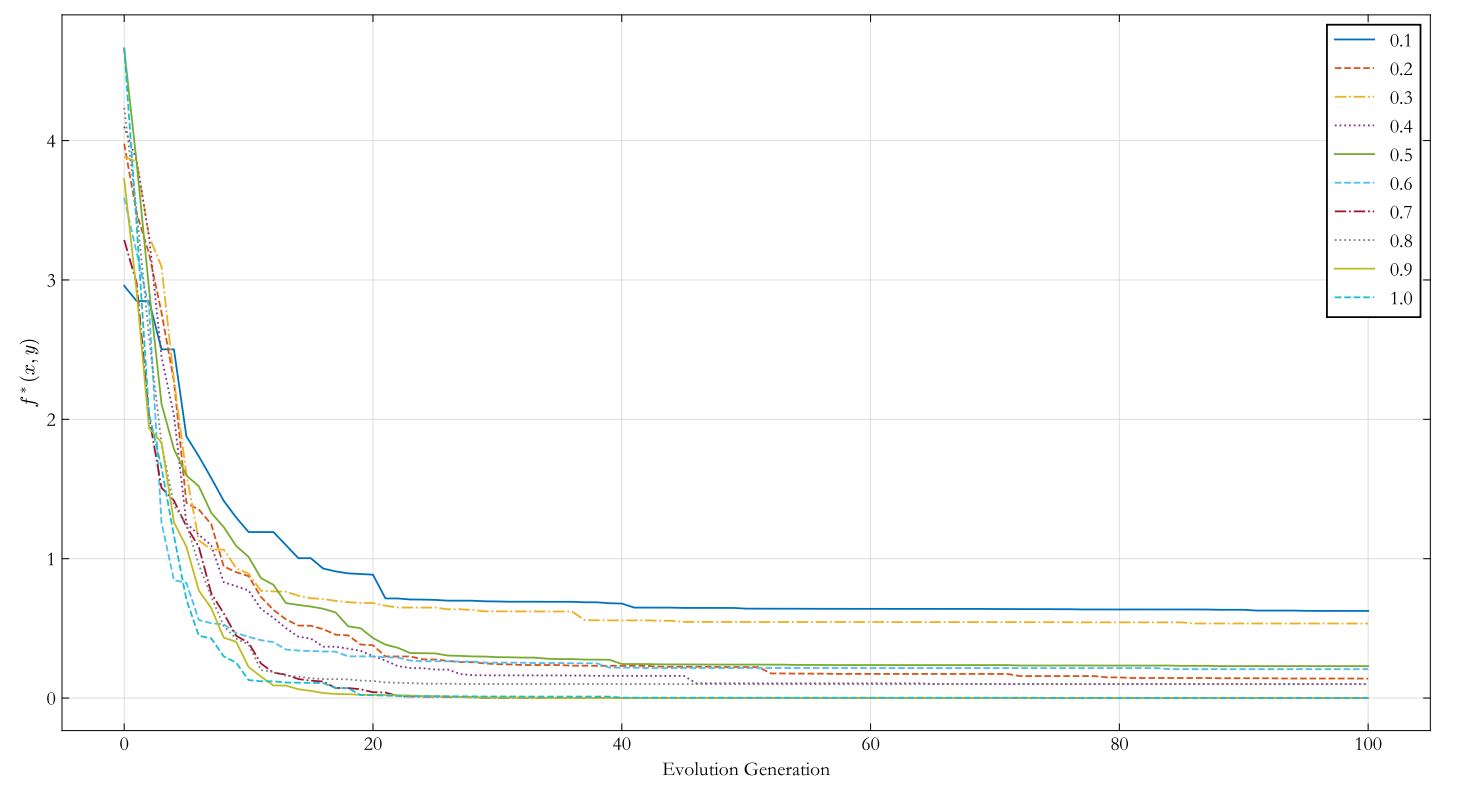
調整變異概率

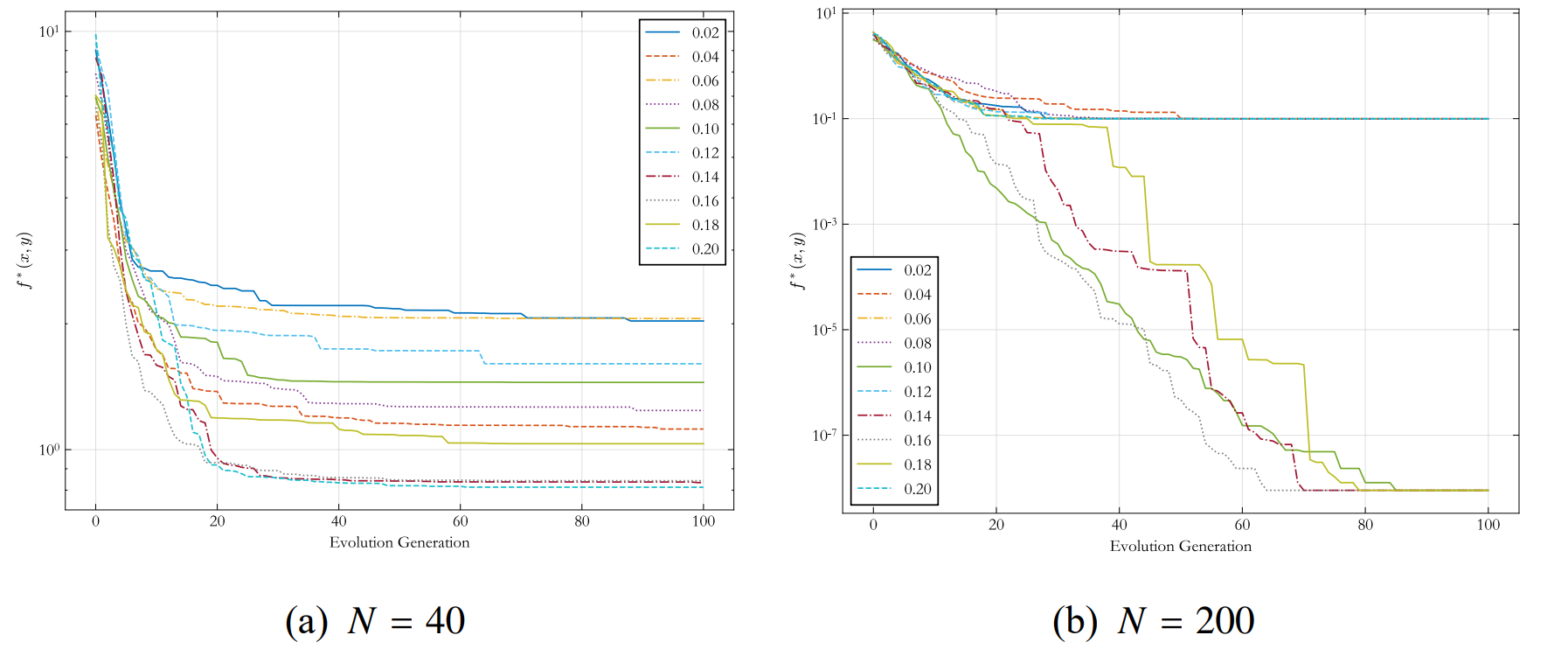
為了更好地體現變異概率變化對演演算法表現的影響，本文分別在種群規模為 40 和 200 的情況下模擬 \([0.02, 0.20]\) 範圍內的 \(P_m\) 對應的迭代曲線。觀察圖 (a) 可以發現種群規模較小時，變異概率越高，染色體進化到更優秀個體的概率也越大，演演算法收斂速度越快。當種群規模擴大到 200 時，過大的變異概率反而會影響演演算法收斂到全域性最優解。

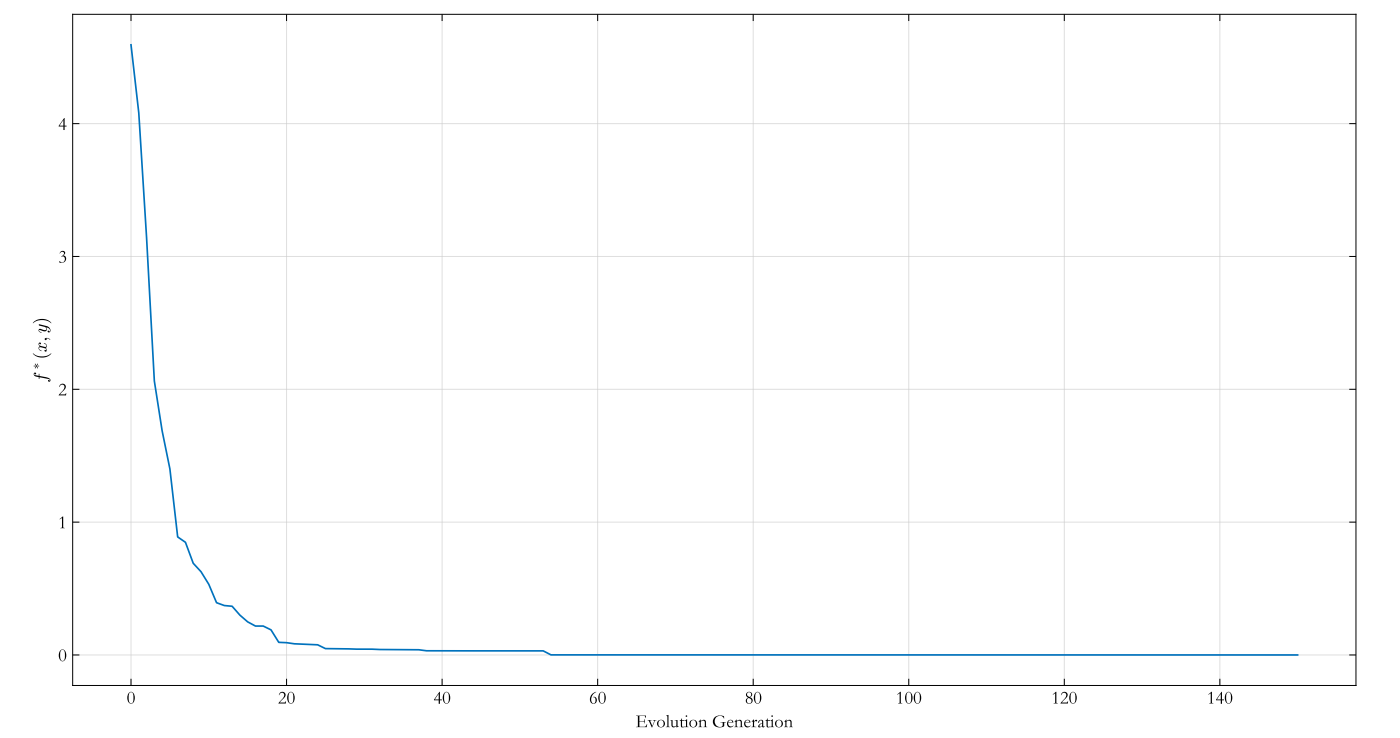
調整迭代次數

本文使用迭代次數作為演演算法的結束條件，由下圖可知當迭代次數較少時，種群還未成熟，演演算法沒有收斂到全域性最優解。當迭代次數達到 60 次時，迭代曲線取向平緩，表明種群已成熟，演演算法已收斂到全域性最優解，此後的迭代對演演算法的貢獻很小，卻帶來了一定的計算開銷。

結論

本文針對遺傳演演算法的引數調節問題，開展基於遺傳演演算法的 Rastrigin 函數優化問題研究。模擬結果表明，種群規模、基因長度、保留的最優染色體比例和迭代次數不能過小或過大，更大的交叉概率可以增大進化出更優秀個體的概率，而更大的變異概率在種群規模較小時也能加速演演算法收斂到全域性最優解的速度。對於遺傳演演算法在其他場景上的應用，可以在這個調參準則的基礎上進行引數選擇，能讓遺傳演演算法有更好的表現。

如何在 Python 中實現遺傳演演算法

前言