原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

譯者：池中物王二狗(sheldon)

原始碼：github: https://github.com/willian12345/coding-curves

第十章螺旋（SPIRALS）

來聊聊螺旋線。

螺旋非常像圓，它是一組點到定圓中心點的距離關係。與圓不同的是，圓的點與中心點距離固定不變，而螺旋上的點與中心點距離是變化的。給定點與中心點的距離通常是由一個基於兩點之間的角度計算得到。所以你需要有函數傳入角度返回半徑。然後你可以通過半徑與角度找到那個角度上對應的點。有很多不同的螺旋公式，會得到不同形態的螺旋。讓我們從最基礎的一個開始。

注：圓有時候也被稱為「退化」的旋轉。「退化」這詞在這裡沒有貶義，只是說圓遵循螺旋的「規則」但又不是通常我們想象中的螺旋。就像一個三角形其中某一邊的長度為 0。所有三角形數學計算通常都能正常工作，但在我們眼中它卻成了一條線。

阿基米德螺旋

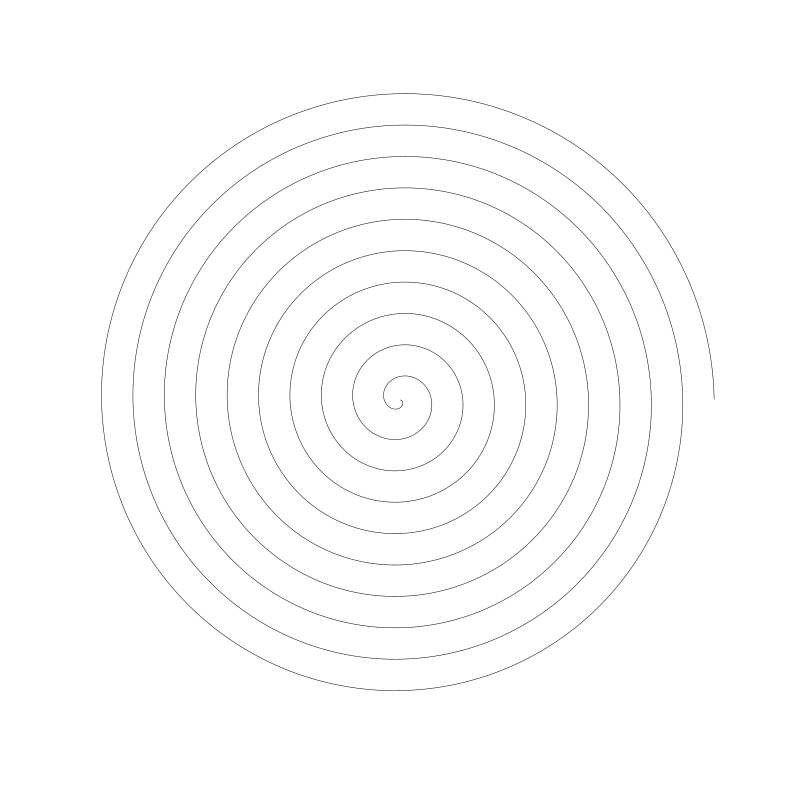
如你所見，每個圓的半徑都會定量增加。下面是這個螺旋線的公式：

r = a * t

此處，t 是弧度 a 是某個常數，上圖中 a 設為 5。兩者相乘的結果即是這個 t 角度上的半徑值。如果將 6 增加到 10，我們會得到如下：

現在如你看到的這樣，常數 a 決定了螺旋內每個圓之間的間距。在這個例子中，螺旋都旋到 canvas 邊界外了。

當我們繪製螺旋時，我們首先需要決定繪製多少個圈。要繞多少圈？如果 t 從 0 到 2 * PI，我們得到的是一個圈:

你可以看到這個螺旋有一個圈，螺旋曲線從中心開始向外擴充套件。三個圈表示 t 從 0 到 2 * PI * 3。

有了上面這些，我們可以將它們合在一起建立一個螺旋線的調式器(playground)，像這樣：

width = 800
height = 800
canvas(width, height)
translate(width / 2, height / 2)
 
cycles = 10
res = 0.01
 
for (t = res; t < 2 * PI * cycles; t += res) {
  r = archimedean(5, t)
  x = cos(t) * r
  y = sin(t) * r
  lineTo(x, y)
}
stroke()
 
function archimedean(a, t) {
  r = a * t
  return r
}

比如我們希望有 10 個圈，迴圈結束點就是 2 * PI * cycles。呼叫 archimedean 螺旋函數，傳入 5 作為它的常數， t 作為弧度。它會返回給我們一個半徑值，我們可以用它和弧度計算出對應點的 x, y 座標並用線連線。

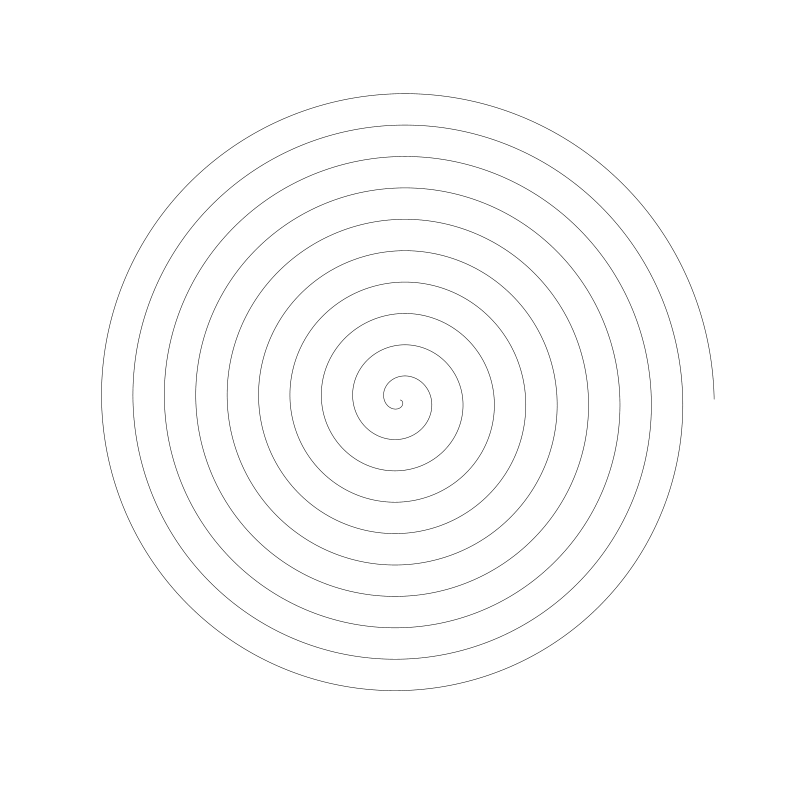
我使用的繪圖 api ，角度正向增加是順時針方向。所以這個螺旋從中心順時針繞出來。這可能與你正在使用的程式設計平臺內表現有所不同。這取決於你使用的繪圖 api 如何處理角度方向。為了翻轉旋轉方向，有幾種方式：

A. 用 scale 翻轉 canvas

scale(1, -1)

B. 改變程式碼建立點的方式，使其中一個軸為負例如：

x = cos(t) * r
y = -sin(t) * r

C. 將回圈的方向變反

for (t = -res; t > -2 * PI * cycles; t -= res) {

任意一種方式都可以讓你的螺旋方向改變。

還有最後一件事...

程式碼中值得注意的一點是迴圈起始點是 res 而不是 0

for (t = res; t < 2 * PI * cycles; t += res) {

想知道為我為啥這麼做，我們需要從下一種螺旋線尋找答案。

雙曲線螺旋 Hyperbolic Spiral

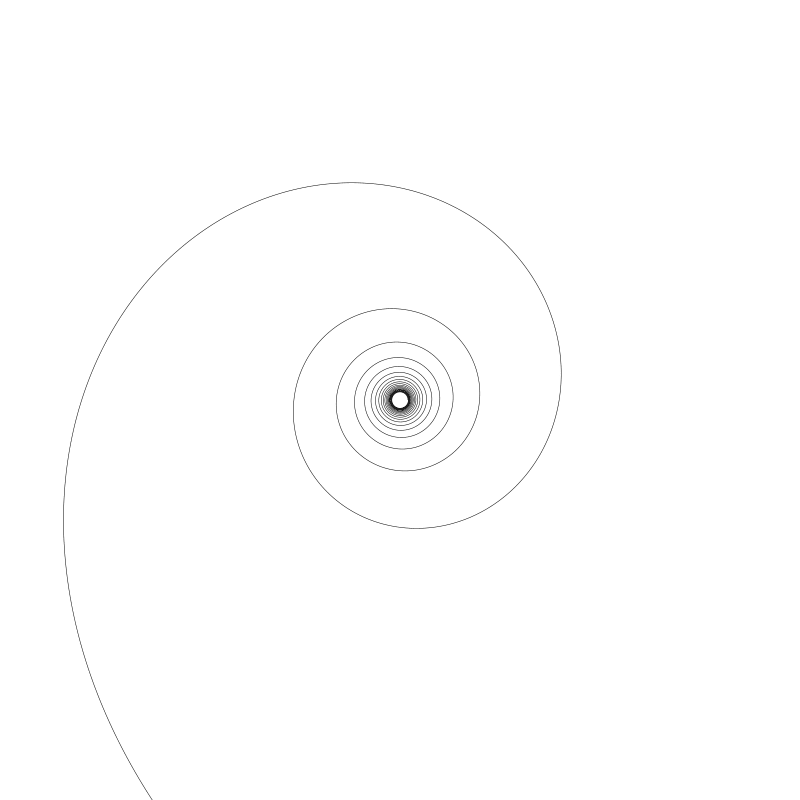
這個螺旋與第一個螺旋看起來非常不同。上個螺旋內每個圈是等距的。你可能會說每個圈之間的距離都增長了，還是等等先別下結論。

下面這個函數是這個螺旋準備的：

function hyperbolic(a, t) {
  r = a / t
  return r
}

也沒有特別大的不同。我們用除代替了乘。上圖我傳入了 1000 。如果我將值降到 10，我們會得到一個很小的螺旋線像這樣：

這就很明顯了 for 迴圈以 res 開始而不是 0，如果是 0，那麼就會出現除數為 0 的這種情況，這會導致某些問題。也許會崩潰，或者半徑為 NaN (not a number) 值, 這沒什麼用。所以我們將起始值設為非 0。

另一個值得注意的事是螺旋線的旋轉方向。上圖我畫了 20 個圈。如果降為 5（a 變回 1000），將得到：

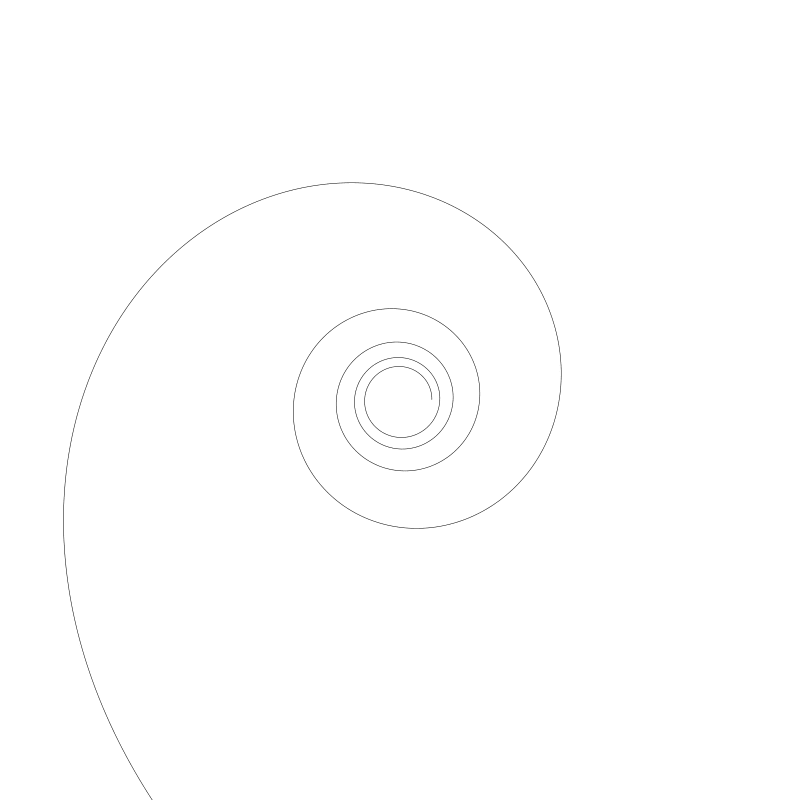
你現在可能看到隨著 t 值增長螺旋變的很大但，但增長的速度慢小了。當有 100 個圈，螺旋中心位置開始有些堵了。

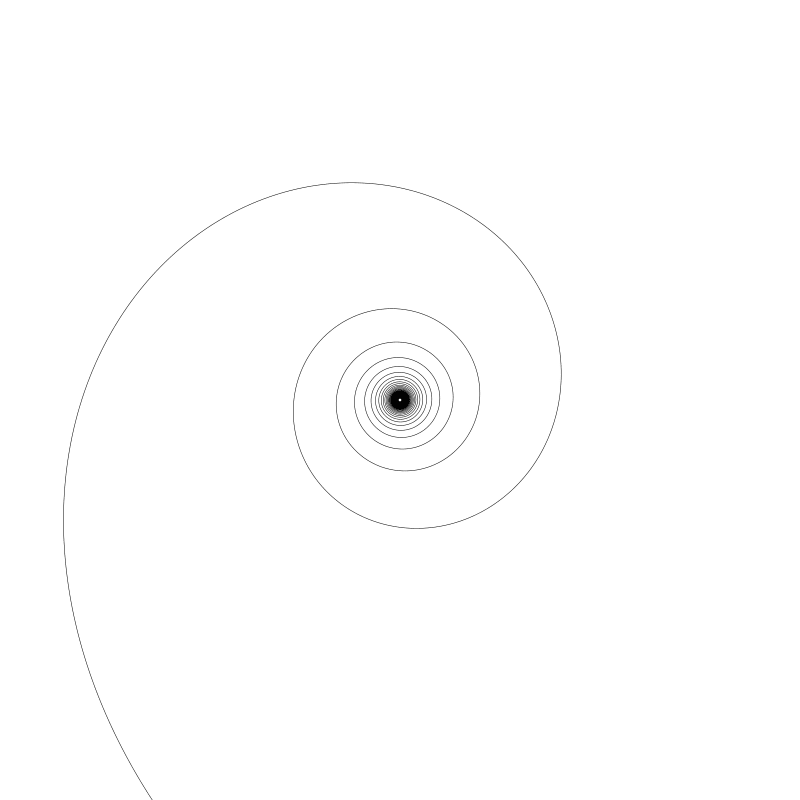
就如我之前所說，咋一看每個圈半徑都在增長，但你現在可以觀察到實際上是開始時很大，但是圈與圈之間的半徑值逐漸變小了。

費馬螺線

這種螺旋線很漂亮。這是公式：

function fermat(a, t)  {
    r = a * pow(t, 0.5)
    return r
}

這裡我們將 a 乘以 t 的 0.5 平方。假定你的程式語言內建了 pow 函數計算第一個引數的第二個引數次冪。根據你使用的程式語言，它可能是這樣：

r = a * (t^0.5)

或這樣：

r = a * (t**0.5)

上一張圖 a 設為了20 繪製了 20 圈。繪製 10 圈結果如下：

可以看到螺旋線是從內向外繪製的。一開始圈與圈之間的間距比較大，但越往外面圈的間距越來越小,還超出邊界了

圈數改回 20 個圈 a 設為 40：

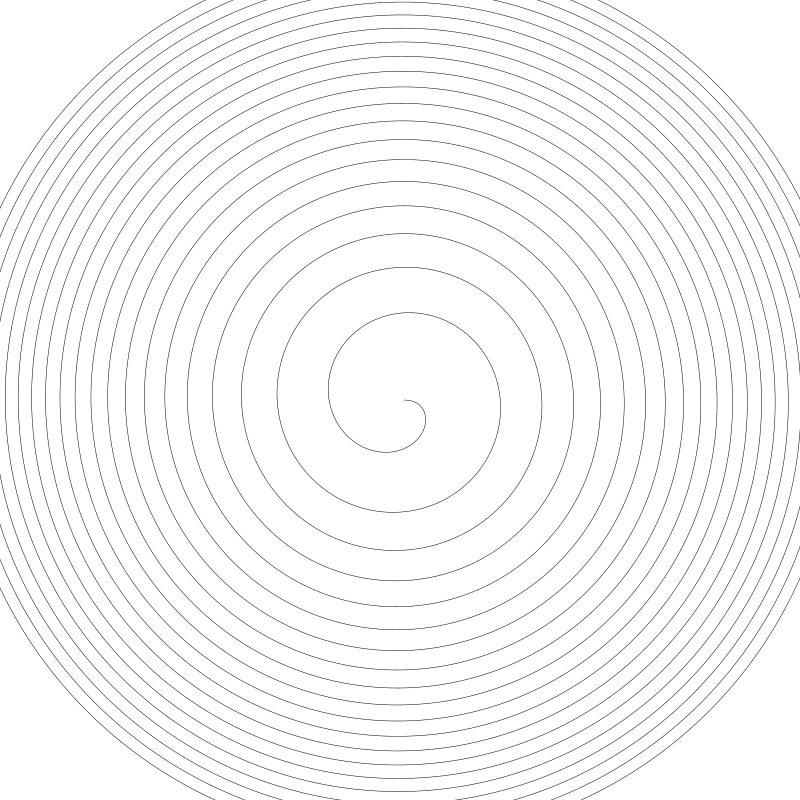
我們能看到間距有所增加。

100 個圈 a 設為 15。

最終，每圈之間已很難有間距。而我們得到了一些有趣的摩爾紋圖案

連鎖螺線 Lituus Spiral

它看起來像雙曲螺線，但公式卻更接近於費馬螺線：

function fermat(a, t)  {
    r = a * pow(t, -0.5)
    return r
}

我們公需要將指數中的 0.5 改為 -0.5。上圖螺旋線繪製了 20 個圈 a 的值為 500。下面是 10 個圈

你可以看到這是另一種向內繪製的螺旋線。改回 20 圈， a 設為 50，得到：

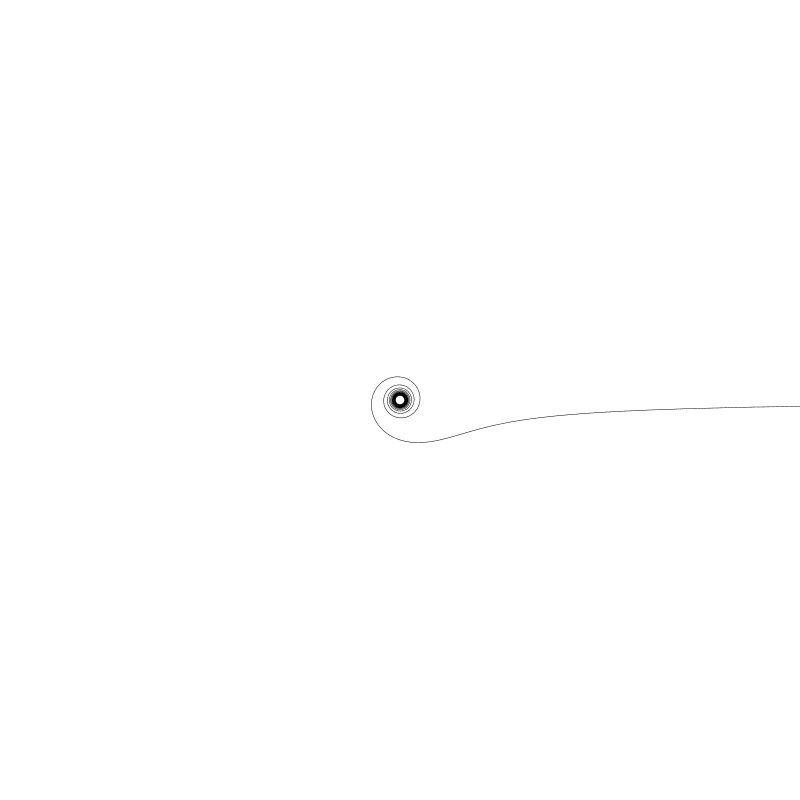
詞「Lituus」原意是彎曲的杖，彎曲的魔法棒或角。上圖很好的解析了它名字的由來。

將 a 升到 1000, 可以得到：

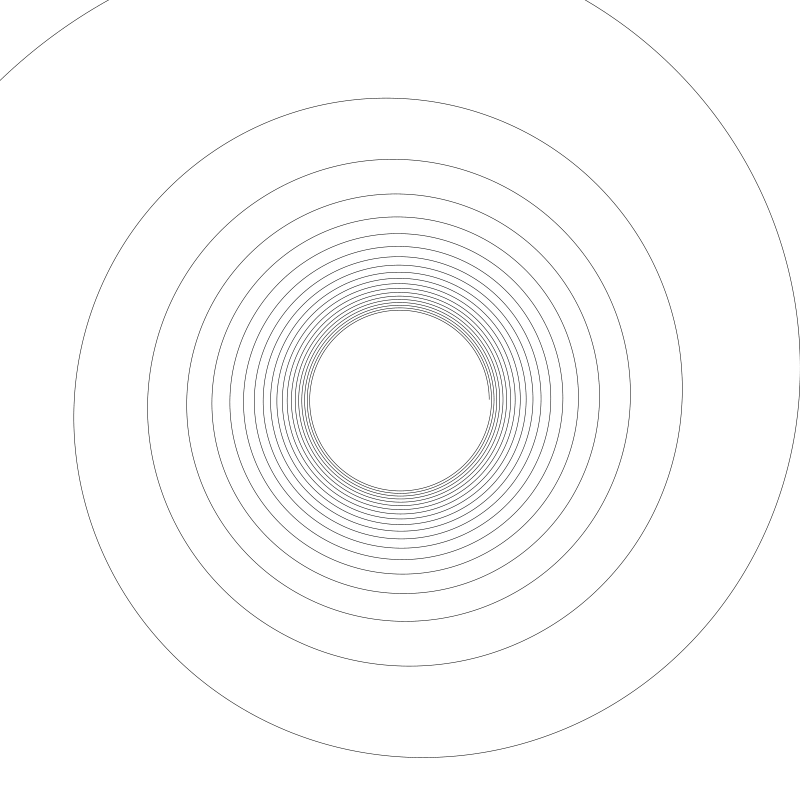
可以這樣講，a 值越低，螺旋吞噬進中心越快。

還有很多型別的螺旋線，來，繼續！

對數螺旋 Logarithmic Spiral

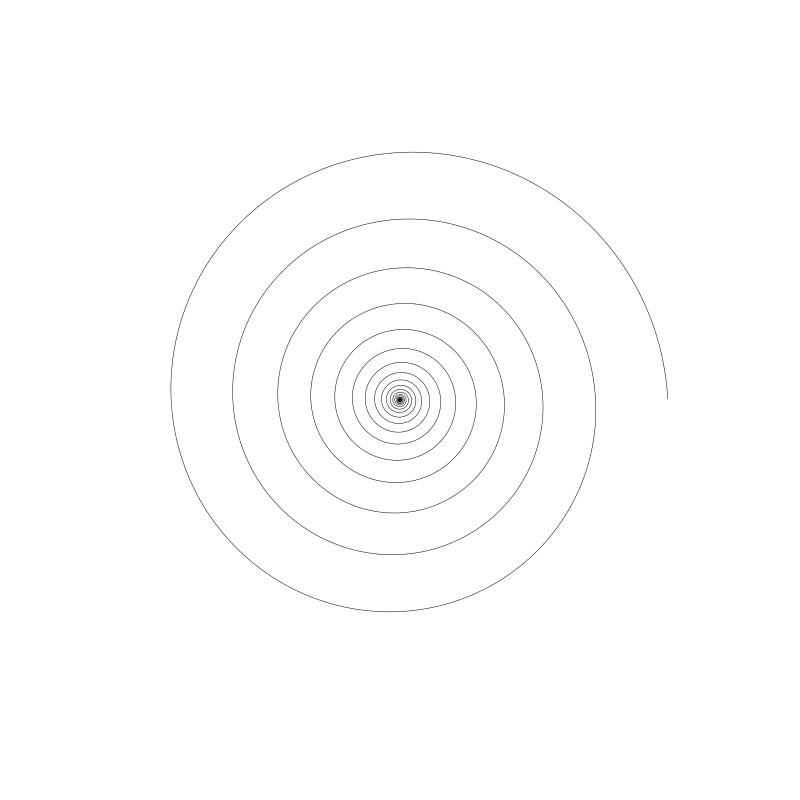
它有點像反費馬螺旋。一開始間隔挺小，越往外越大。公式：

function logarithmic(a, k, t)  {
    r = a * exp(k * t)
    return r
}

公式看起來比之前遇到過的要複雜一點。t 前有兩個引數。我們先從 exp 函數開始學習。

我們實際上在諧振波圖(Harmonographs) 這一章見過它. 回顧一下，有一個數學常數 e ，也稱尤拉數。它的值大概是 2.71828。當我們在與對數打交道時，常將 e 乘方。所以很多數學程式庫會直接提供一個函數，常被命名為 exp。舉個具體的例子，在 javascript 中，有常用 e, Math.E。為了計算 e 的 2 次冪，就得像下面這樣做：

Math.pow(math.E, 2)

但其實已經有一個叫 exp 的函數了，你可以直接用：

Math.exp(2)

程式碼中的公式也得改成，

r = a * exp(k * t)

我們用 a 乘以 e 的 k * t 次冪。上面的圖，我得將 a 設成 0.5 且將 k 設為 0.05。

如果將 a 變為 1，我們將得到一個相當大的螺旋線，雖然它們看起來很像。

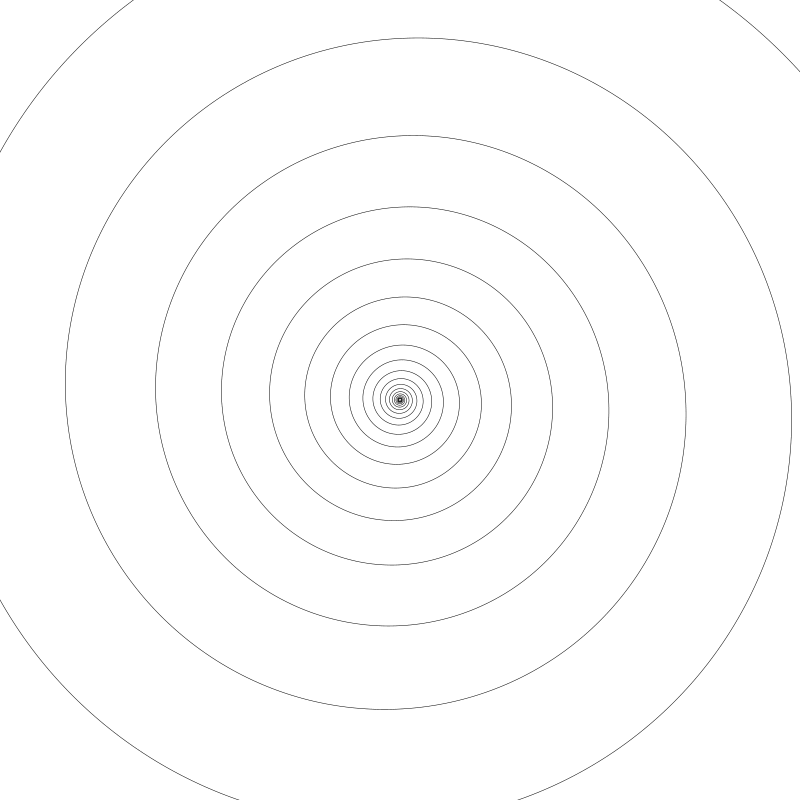
a 設為 0.24 後：

還是挺像的，但更小一點兒了。

將 a 重置為 0.5 並且將 k 升到 0.1

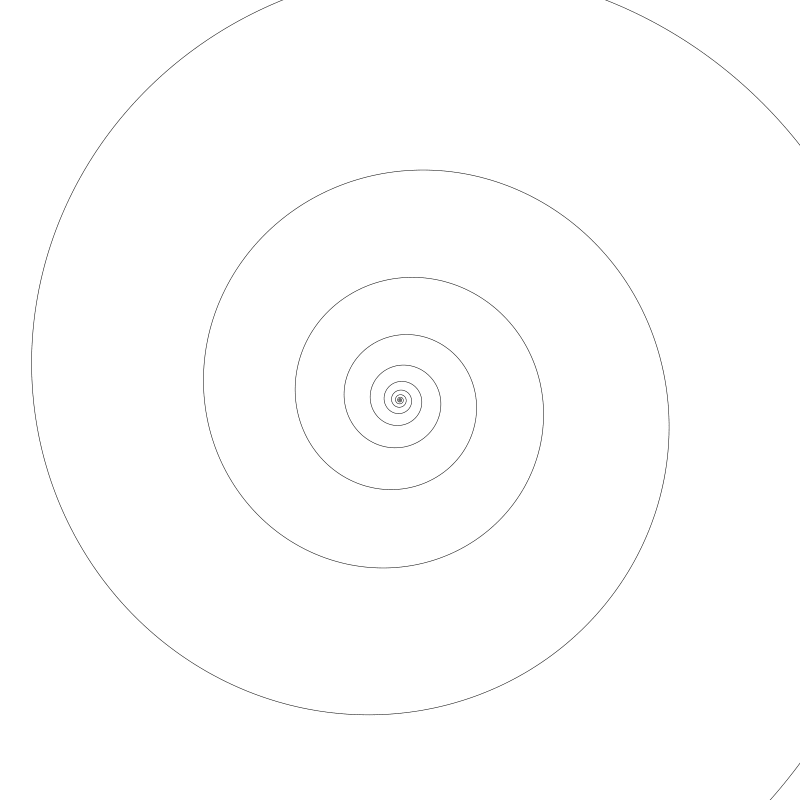
你可以看到擴張的更快了。將 k 設為 0.04 它對結果的影響遠超我的預期

黃金螺旋（Golden spiral）

這類螺旋增長率叫「黃金比例」，大概接近 1.618。它的公式是：

function golden(t) {
    r = pow(PHI, 2 * t / PI)
    return r
}

首先，這個函數除了 t 之外沒有其它引數。 PHI 黃金比例值是寫死在函數內的。很多數學程式庫都有黃金比例這個內建常數。如果你沒有，將這近似的設定為：

PHI = 1.61803

或者你想更精確一點，你可以像下面這樣寫得到精確值：

PHI = (1 + sqrt(5) ) / 2

然後放在某個地方按需參照即可。

你很可能已經見過這種螺旋圖了：

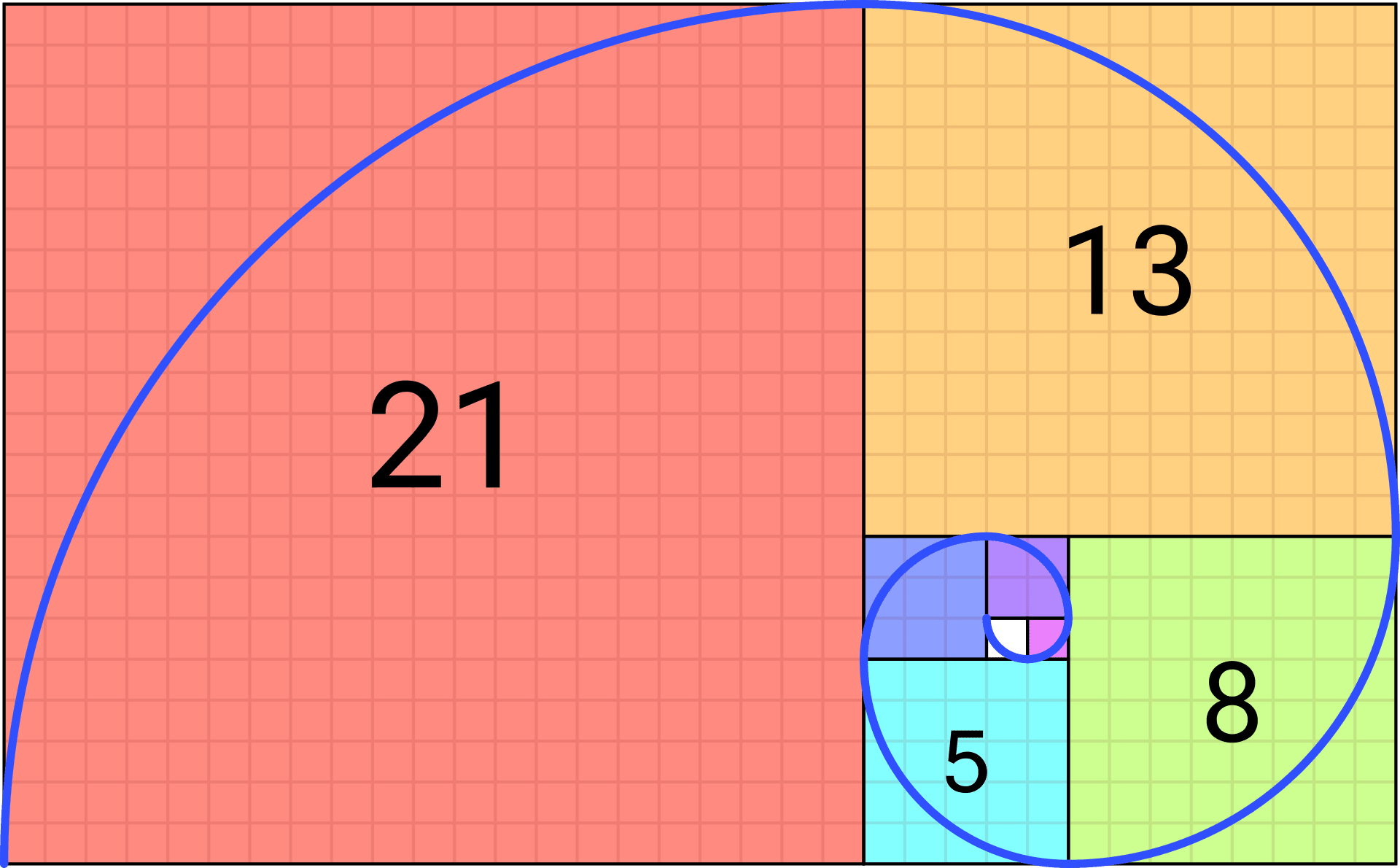
By Romain – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=114415511

這實際是一個斐波那契螺旋。方塊大小是下兩個方塊之和且每個方塊內的曲線是一個角為中心 90 度生成弧線。它不是精確的黃金螺旋，但很接近了。

還有更多

仔細閱讀這個螺旋線列表，也許你能找到其它更有趣的

https://en.wikipedia.org/wiki/List_of_spirals

還有：

https://mathworld.wolfram.com/topics/Spirals.html

螺旋角（Spirangles）

在寫這一章的時候我偶然發現了這個詞 (Spirangles)。本質上它是由直線線段組成的螺旋。通過改變每個線段的角度，你可以將它們組成不同的形狀。

在已有的基礎上實現它非常容易。上面中有個例子使用的是 archimedean 函數，a 為 3，並且 cycles 為 20。竅門是減低解析度 res 上圖的效果我是將 res 設為了發下值：

res = PI * 2 / 3

Now on each step of the for loop, t will increase by one-third of a circle. Here are some others, dividing by 4 and 5.

現在，迴圈中每一步，t 會增加 1/3 個圓。以下是其它，除 4 和除 5 的效果：

竅門你已經知道了。你可能想在其它方法上試試。其中一些通過這樣修改後變的讓人相當滿意。

葵花螺旋（Sunflowers）

若是沒有討論葵花螺旋，那麼螺旋這一篇就不算完整。試試用葵花，斐波那契與螺旋的組合搜尋，你能得到巨量的閱讀材料與漂亮圖片。我的意思是，除了繪製葵花螺旋這類有趣的螺旋線外，其它的螺旋我就讓你自己去探索了。黃金比例在這個圖中是天生的，圖是這樣：

你可以看到不止一條螺旋，有許多螺旋以不同角度進進出出。我常用下面的程式碼實現（還是以虛擬碼展示）：

width = 800
height = 800
canvas(width, height)
translate(width / 2, height / 2)
 
count = 1000
for (i = 0; i < count; i++) {
  percent = i / count
  size = 14.0 * percent
  r = 380.0 * percent
  t = i * PI * 2 * PHI
  x = cos(t) * r
  y = sin(t) * r
  circle(x, y, size)
  fill()
}

我們用變數 count 代表想要繪製多少「葵花籽」。這裡 count 設為了 1000.

然後我們迴圈用 i / count 得到一個百分比值。

變數 size 是每顆「種子」的半徑。當 i 越接近 count 時，percent 的值會越接近 1，因此 size 的值也會越接近最大值 14。

同樣 r 用於表示種子分佈的半徑。它最高值是 380，僅比 canvas 寬度的一半小一點點。

我們用 t = i * PI * 2 * PHI 計算出 t ，它就是神奇的葵花斐波那契公式。說真的，你想知道更多，那就認真看一下。有了角度和半徑，我們就可以得到 x 和 y 座標，然後根據種子自己的大小繪製種子了。

到目前為止我想說的螺旋線就這麼多了。下回見！

本章 Javascript 原始碼 https://github.com/willian12345/coding-curves/blob/main/examples/ch10

部落格園: http://cnblogs.com/willian/
github: https://github.com/willian12345/

曲線藝術程式設計 coding curves 第十章 螺旋曲線（SPIRALS）

第十章 螺旋（SPIRALS）