一.樹結構之二元樹操作

二元樹的查詢

二元搜尋樹，也稱二叉排序樹或二叉查詢樹

二元搜尋樹：一棵二元樹，可以為空，如果不為空，應該滿足以下性質：

非空左子樹的所有結點小於其根結點的鍵值
非空右子樹的所有結點大於其根結點的鍵值
左右子樹都是二元搜尋樹

對於二元樹的查詢，其實沿用的是分治法的思想，所以我們的樹一定是要排序好的，這樣才能使用每次檢索都少一半的資料量

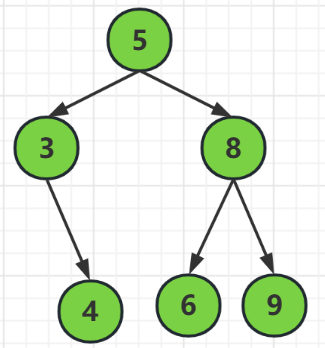
我們可以看到上面的二元樹，它滿足根結點的左邊都比根結點小，而右邊又都比根結點大，所以它就是可以使用二元樹查詢的

當我們要查詢6時

首先，我們對根節點進行比較，發現6是大於5的所以，我們需要去根結點的右邊也就是結點8

然後，結點8進行對比，發現它比結點8小，所以去結點的額左邊也就是結點6

最後，結點6和查詢鍵值6是一樣的，所以找到了

以下是程式碼實現：

Position Find(ElementType x, BinTree BST) {
    if (!BST) {
        return NULL;
    }
    if (x > BST->Data) {
        return Find(x, BST->Right);
    }
    else if (x<BST->Data){
        return Find(x, BST->Left);
    }
    else{
        return BST;
    }
}

我們可以發現，使用遞迴實現的程式碼查詢，其實是尾遞迴，對於尾遞迴，我們可以直接使用迴圈來做

利用迴圈的程式碼實現：

//將尾遞迴轉換為迴圈，效率高
Position IterFind(ElementType x, BinTree BST) {
    while (BST) {
        if (x > BST->Data) {
            BST = BST->Right;
        }
        else if(x<BST->Data){
            BST = BST->Left;
        }
        else
            return BST;
    }
    return NULL;
}

二元樹的插入

插入結點的關鍵在於要找到結點的位置，我們可以使用查詢函數的思維，找到它的位置，然後再對應插入

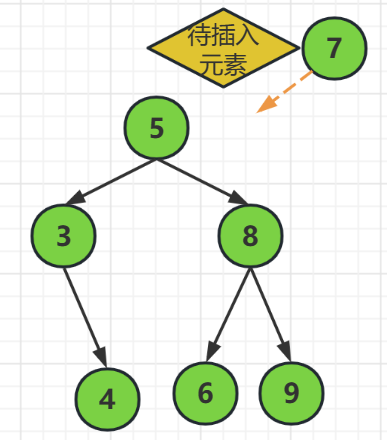
上面的圖片，我們要插入元素7到樹中去，

首先，元素7是大於根節點5的，所以元素7應該處於根結點的右邊位置，就和結點8進行比較

然後，發現結點8是大於元素7的，所以我們元素7因該在結點8的左邊，也就是到了結點6的位置，

最後，結點6左右無元素，且元素7大於結點6，所以元素7位於結點6的右子結點

然後是程式碼實現：

BinTree Insert(ElementType x, BinTree BST) {
    if (!BST) {
        BST = malloc(sizeof(struct TreeNode));
        BST->Data = x;
        BST->Left = BST->Right = NULL;
    }
    else {
        if (x < BST->Data) {
            BST = Insert(x, BST->Left);
        }
        else if (x>BST->Data) {
            BST = Insert(x, BST->Right);
        }
        return BST;
    }
}

二元樹的刪除

刪除的情況要複雜一些，因為我們的樹分有子結點和無子結點，當然無子結點的肯定是很好刪除的，主要是有子結點的怎麼刪除呢？

這就需要我們分情況討論：

無子結點時：

直接刪除需要刪除的結點，並修改其父結點的指標，置為NULL

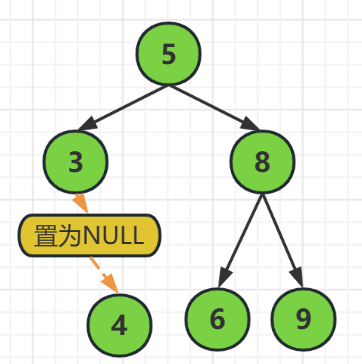
如上圖，

當我們要刪除結點4的時候，結點4自己是沒有子結點的，

所以我們可以直接釋放結點4，並且把結點3的右結點指標指向NULL

當有一個子結點的時候：

需要把要刪除的結點的父結點指標，指向它的孩子結點，相當於中間少了一層

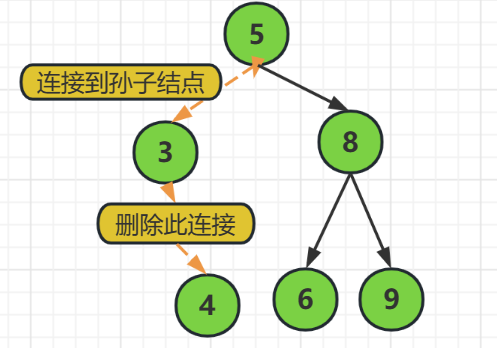
如上圖，

我們要刪除結點3的時候，發現它是有一個結點4的，我們就不能直接把結點3刪除了

而是要先把結點5的指向結點3的指標指向結點4

然後再釋放結點3

當有兩個子節點的時候：

這種情況使用的方法是，要麼使用左子樹的最大元素頂上去，要麼使用右子樹的最小元素頂上去

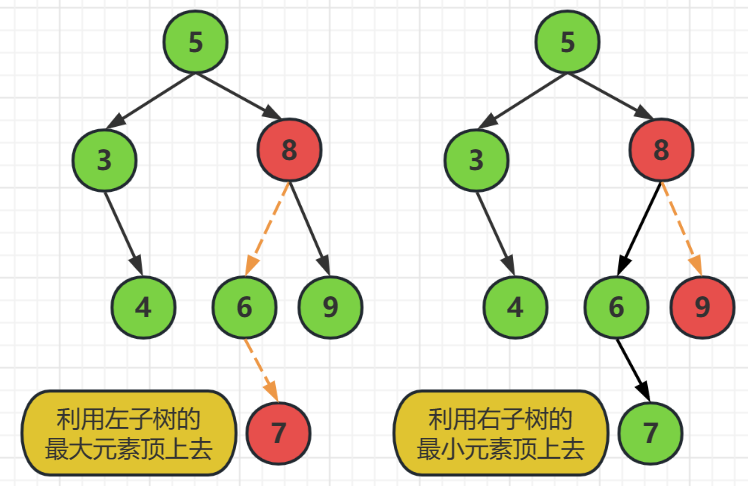
這裡需要刪除的結點是8，

我們可以在左子樹中去找到最大的元素，然後替換到結點8的值，然後刪除結點7就可以了

還可以去右子樹中找到最小的元素，然後替換掉結點8為最小結點的值，然後刪除最小結點

注意：

刪除結點時需要改變父結點指標指向為NULL

當刪除的結點後面還有結點時，要一個一個的連線到前面來

然後就是程式碼實現：

// 查詢最小結點
Position FindMin(BinTree BST) {
    if (!BST)
        return NULL;
    else if (!BST->Left)
        return BST;
    else
    {
        return FindMin(BST->Left);
    }
}


//刪除結點
BinTree Delete(ElementType x, BinTree BST) {
    Position Temp;
    if (!BST)
        printf("要刪除的元素未找到！");
    else if (x < BST->Data) {
        BST->Left = Delete(x, BST->Left);
        //在左子樹查詢要刪除的元素
    }
    else if (x > BST->Data) {
        BST->Right = Delete(x, BST->Right);
        //在右子樹查詢要刪除的元素
    }
    else
        //找到要刪除的結點
    {
        if (BST->Left && BST->Right){
            //左右都有結點
            Temp = FindMin(BST->Right);
            //找右子樹的最小元素
            BST->Data = Temp->Data;
            //把右子樹最小元素覆蓋到要刪除的元素上
            BST->Right = Delete(BST->Data, BST->Right);
            //刪除右子樹的最小元素
        }
        else
        {// 只有一個結點的情況，或沒有結點的情況
            Temp = BST;
            if (!BST->Left) {
                //右結點存在，或沒有結點存在
                BST = BST->Right;
            }
            else if (!BST->Right) {
                //左結點存在，或沒有結點存在
                BST = BST->Left;
            }
            free(Temp);
    }
    }
    
    return BST;
}

二.進階之平衡二元樹（AVL樹）

什麼是平衡二元樹？

平衡二元樹（AVL樹）：空樹，或者任一結點左，右子樹的高度差絕對值不超過1，即| BF_（T）<=1 |

平衡因子：BF_(T) = h_L - h_{R ，}其中h_L，h_R是T的左子樹高度和右子樹高度

我們可以來看幾個圖分別一下是不是平衡二元樹：

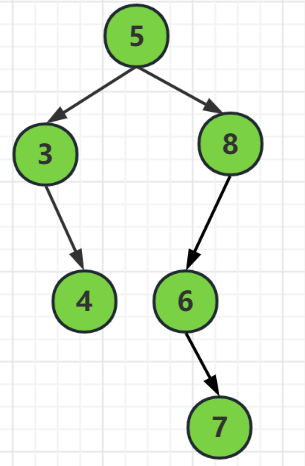
上圖，對於結點5來說，左子樹高度2，右子樹高度3

3 - 2 = 1 滿足 | BF_（T）<= 1 |

但是對於右子樹的結點8來說，它的左子樹高度是2，右子樹高度為0

2-0 = 2就不滿足 | BF_（T）<= 1 |

所以這不是一棵平衡二元樹

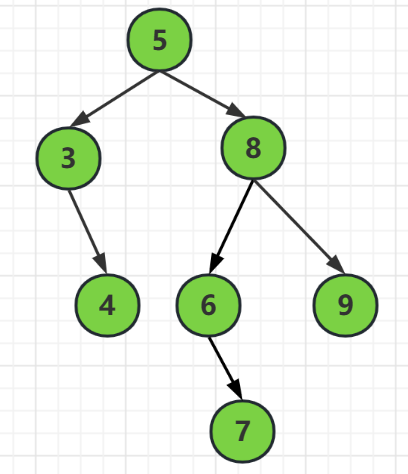
對於這顆樹來說，

結點5 的左子樹高度是2，右子樹高度是 3，滿足最小高度為小於等於 1

結點8 的左子樹高度是2，右子樹高度是1，滿足最小高度為小於等於 1

所以它是一棵平衡的二元樹

平衡二元樹的調整

平衡二元樹在建樹的時候其實是平衡的，主要是在後期的插入和刪除中，會破壞掉它的平衡，最常見的就是插入就破壞了平衡，即 | BF_（T）>1 | ，它就不滿足平衡二元樹了

所以我們在插入的時候，會有一個二元樹的平衡調整的過程

RR旋轉（右單旋轉）------

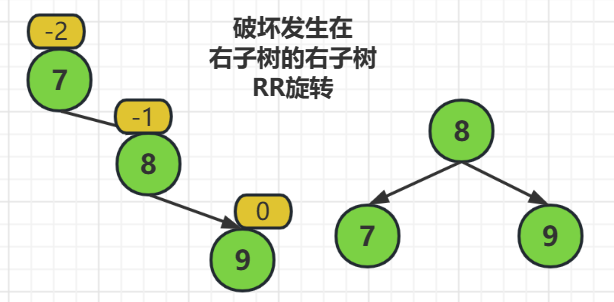
RR旋轉指的就是，破壞發生在右子樹的右子樹，

解決方式就是把被破環的結點，也就是結點7的右子樹作為它們的父結點，相當於把結點7提起來做父結點

由於我們的平衡二元樹在調整的時候也需要注意滿足查詢二元樹的準則，所以對被提起來的結點，它左邊的結點需要掛到它父結點的左邊

也就是說，把結點8做父結點提起來的時候，結點8的左子樹要掛在結點7的右邊

LL旋轉（左單旋轉）------

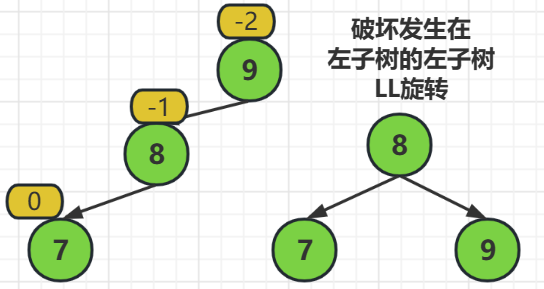
LL旋轉指的是，破壞發生在左子樹的左子樹

解決方式就是把被破壞的結點的子結點，提起來當作父結點，而原來的父結點當作子結點

也就是結點8被當作父結點，而原來的結點7被落下去當子結點了

由於平衡二元樹在被調整以後依然要滿足查詢二元樹的準則，所以我們需要把被提起來的結點的右子樹，放在落下去結點的左子樹

也就是，原來結點8的右子樹要放在現在結點9的左子樹（存在的情況下）

LR旋轉 ----------

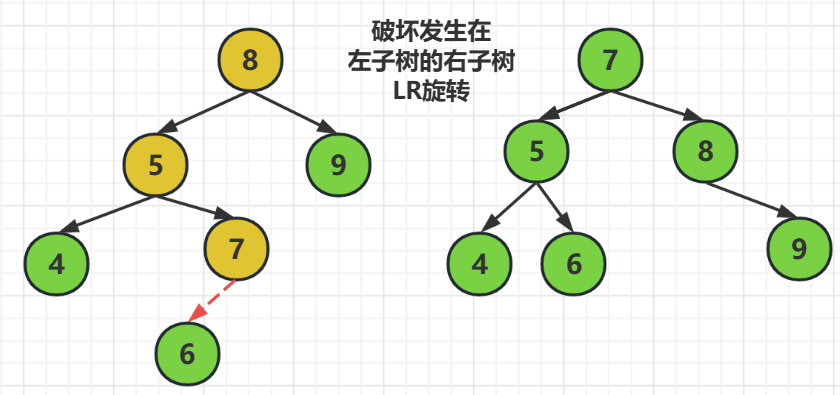
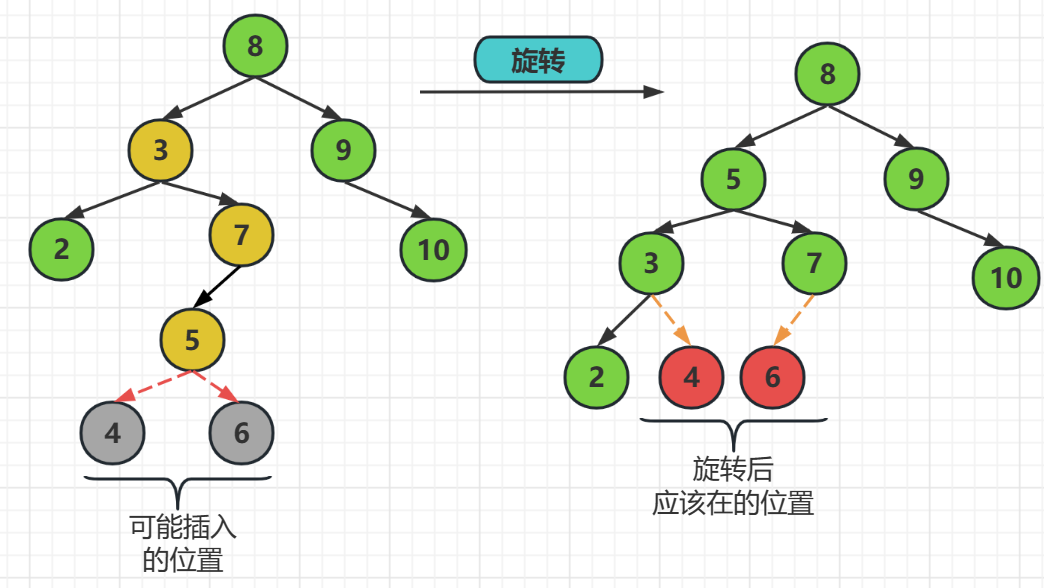
LR旋轉指的是，破壞發生在左子樹的右子樹上

解決方式就是發生把發生破壞的結點提起來左父結點，而原來的左子樹結點繼續做左子樹結點，原來的父結點做右結點

注意這時的波壞結點可能是插入了結點的，如果它插入在左邊，那麼他就是原來左子樹結點的右子樹，如果它插在破壞結點的右邊，那麼它就應該在原父結點的左邊

也就是，在結點8，結點5，結點7中，結點7要被提起來做父結點，結點5繼續做它的左子樹結點，而原來的父結點8做新父結點的右子樹

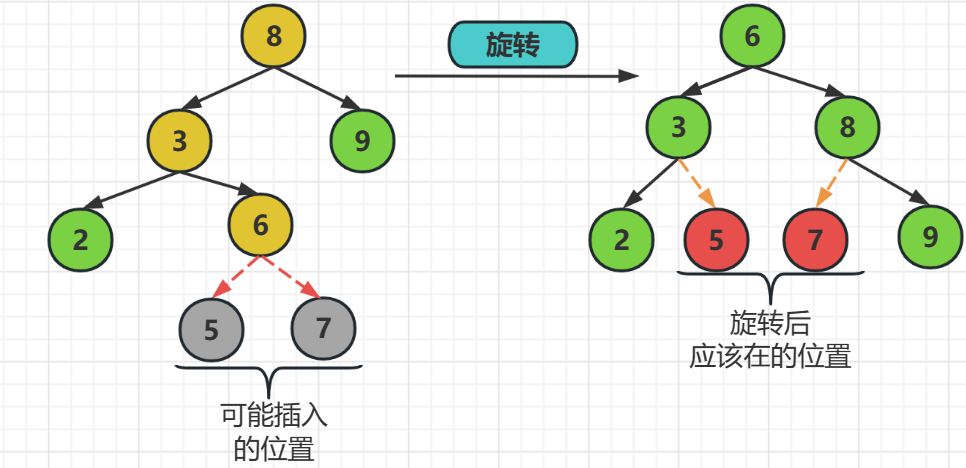
對於新插入的元素6，由於它是插入在結點7的左邊，所以它是結點5的右子樹，當然他要是插在了結點7的右邊，那麼它就是結點8的左子樹

解釋如下：

RL旋轉 ---------

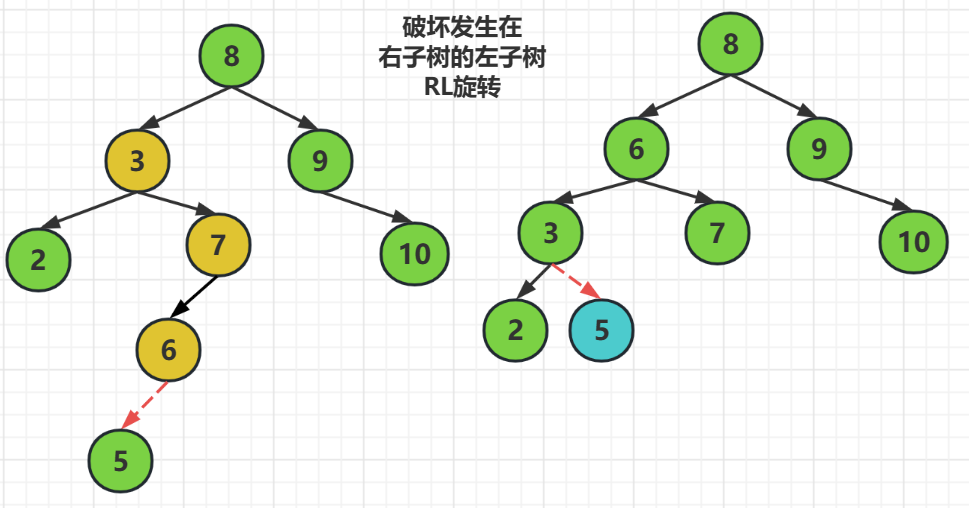
RL旋轉指的就是，破壞在右子樹的左子樹

解決方式就是把破壞結點提起來做父結點，原來的父結點做新父結點的左子樹，而原來的右子樹還是新父結點的右子樹

由於我們平衡二元樹調整後還要滿足查詢二元樹，所以對於插入破壞結點左邊的數要在新的左子樹的右邊，而插入到破壞結點右邊的數要在新的右子樹的左邊

也就是，把結點6提起來做新的父結點，原父結點3做結點6的左子樹，而右結點則還是結點7，

對於原來插入到結點6左邊的數要在新的左子樹3的右邊，而插入在結點6的右邊的，要在新的右子樹的左邊

解釋如下：

三.樹的應用

對於一棵二元樹來說，它可以有多個輸入序列，但是，構成的可能是同一棵二元樹，那麼我們怎麼根據輸入序列來判斷是不是同一棵二元樹呢？

不建樹的判別方法：

如：

3，1，2，4

3，4，1，2

由於第一個元素肯定是根結點，所以根結點就是3，並且比根結點小的在左邊，比它大的在右邊

所以被分成了

{1，2} ，3，{4}

我們可以看到它們此時的序列是完全一樣的，所以可以構成一棵二元樹

在如：

3，1，2，4

3，2，4，1

一樣的方法劃分，3為根結點

{1，2}，3，{4}

{2，1}，3，{4}

對於左邊來說，第一個元素是下一層的根結點，

所以一個是1為父結點，一個是2為父結點，顯然不是同一顆二元樹

建一棵二元樹，其它序列來依次對比：

typedef struct TreeNo* Tree;
struct  TreeNo
{
    int v;
    Tree Left, Right;
    int flag;
};

這是我們需要使用到的結構

我們對於多個輸入序列，只會構建一棵二元樹，然後就是讓序列對已經構建好的二元樹進行遍歷，其中flag有重要的作用

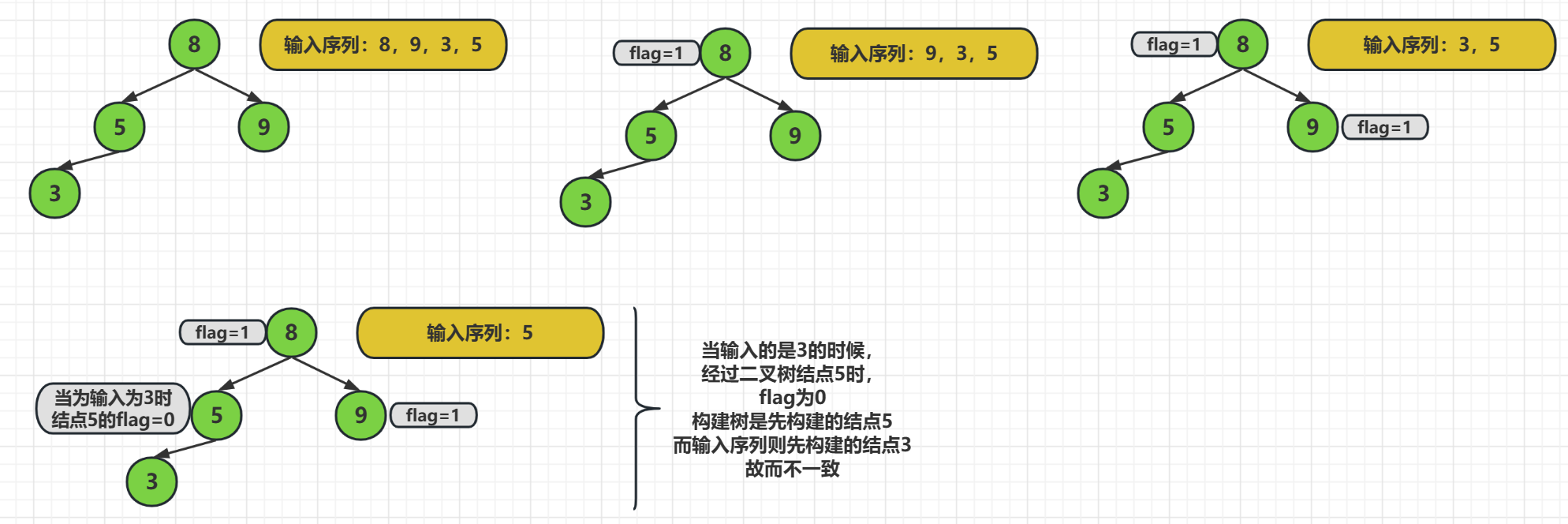
這種方法來判定二元樹是否同構的思想是，

我們已經構建好了一棵二元樹，然後只需要對輸入序列依次存取，

如果被存取的結點flag為0，那麼就給flag賦值為1，

如果不是被存取結點，但是存取過了也就是flag為1，那麼可以向下尋找，

如果不是被存取的結點，但是flag也不為1，那麼則表示不同構

原因是，它們兩個結點的構建的位置不一樣，可以看上面的圖片，輸入序列要先構建3為父結點，而已構建的二元樹則使用結點5作為父結點，說以兩個二元樹不同構

四.紅黑樹--拓展

紅黑樹（Red Black Tree）是一種自平衡二叉查詢樹，是在電腦科學中用到的一種資料結構，典型的用途是實現關聯陣列

紅黑樹的特性：

根結點是黑色的
葉子結點（null值）黑結點
紅結點的子結點必須是黑結點
新插入的結點是紅色的結點
父結點到任一葉子結點黑結點數相同

紅黑樹也是一種自平衡的二元樹，但是它比二叉平衡樹的條件更加寬泛，

二叉平衡樹所要求的平衡是左子樹和右子樹的高度相差小於等於1

而紅黑樹的要求是父結點到葉子結點的黑節點數相同就可以了，這個條件其實是很寬泛的了，我們可以找出它的一種極端情況，那麼就是左子樹都是黑色，而右子樹黑紅交叉，

這種情況構建的紅黑樹，它右半邊的結點數其實是左邊的2n-1

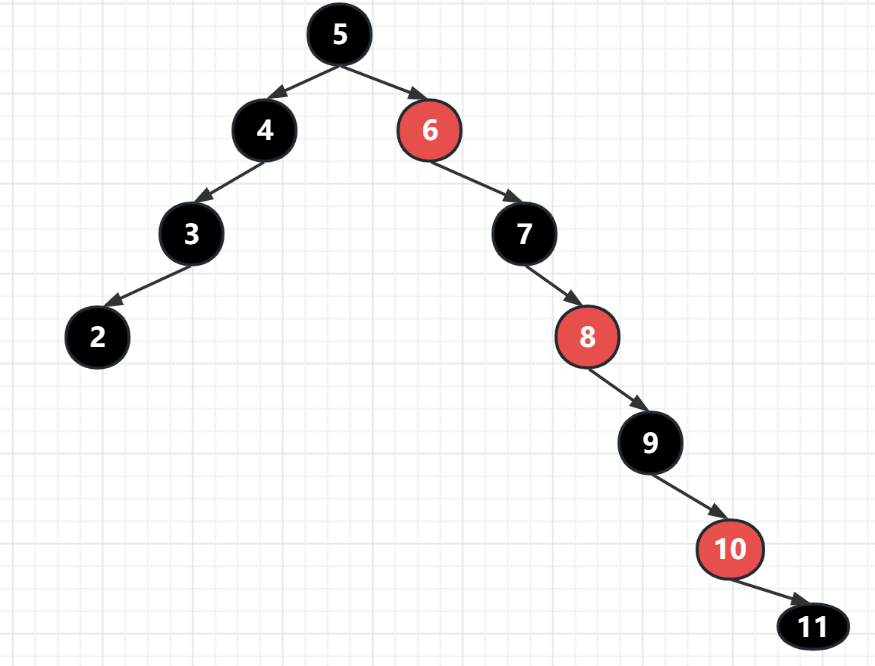
假如有一顆這樣的樹，其實不存在，因為很多右子樹，左子樹都沒資料，是構成不了紅黑樹的，

我們看到它左邊的長度是3，而右邊則是6，很顯然比左邊多出了一倍，那麼還能叫自平衡樹嗎？

這就是紅黑樹的平衡，我們可以把紅結點都去掉，發現黑節點其實是平衡的，更重要的是，就算加上紅結點，其實上面的查詢的時間複雜度也是O(2 * log₂ⁿ)

由於我們的常數是不用記錄到時間複雜度的，所以依舊是 log₂ⁿ

所以紅黑樹給出的平衡指的是：左子樹和右子樹的結點相等或相差一倍，都是可以的

為什麼紅黑樹這樣定義平衡呢？

我們可以直到AVL二元樹它的平衡過於嚴格，所以每次插入都可能有很大的變化，大多數插入的時間都花在了維持那嚴格的平衡上了

而寬泛的紅黑樹，則變動更少，它的平均效能又很高，它能保證很高的效能，而又插入不會頻繁的發生變更，所以紅黑樹就使用自己定義的那套平衡機制

紅黑樹的構造過程：

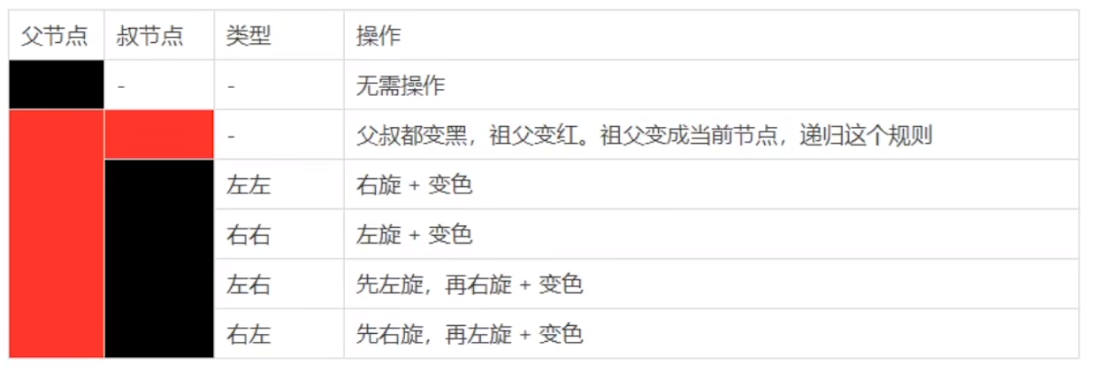
上面的圖片就是紅黑樹的構造規則，我們可以簡單的來實現一下：

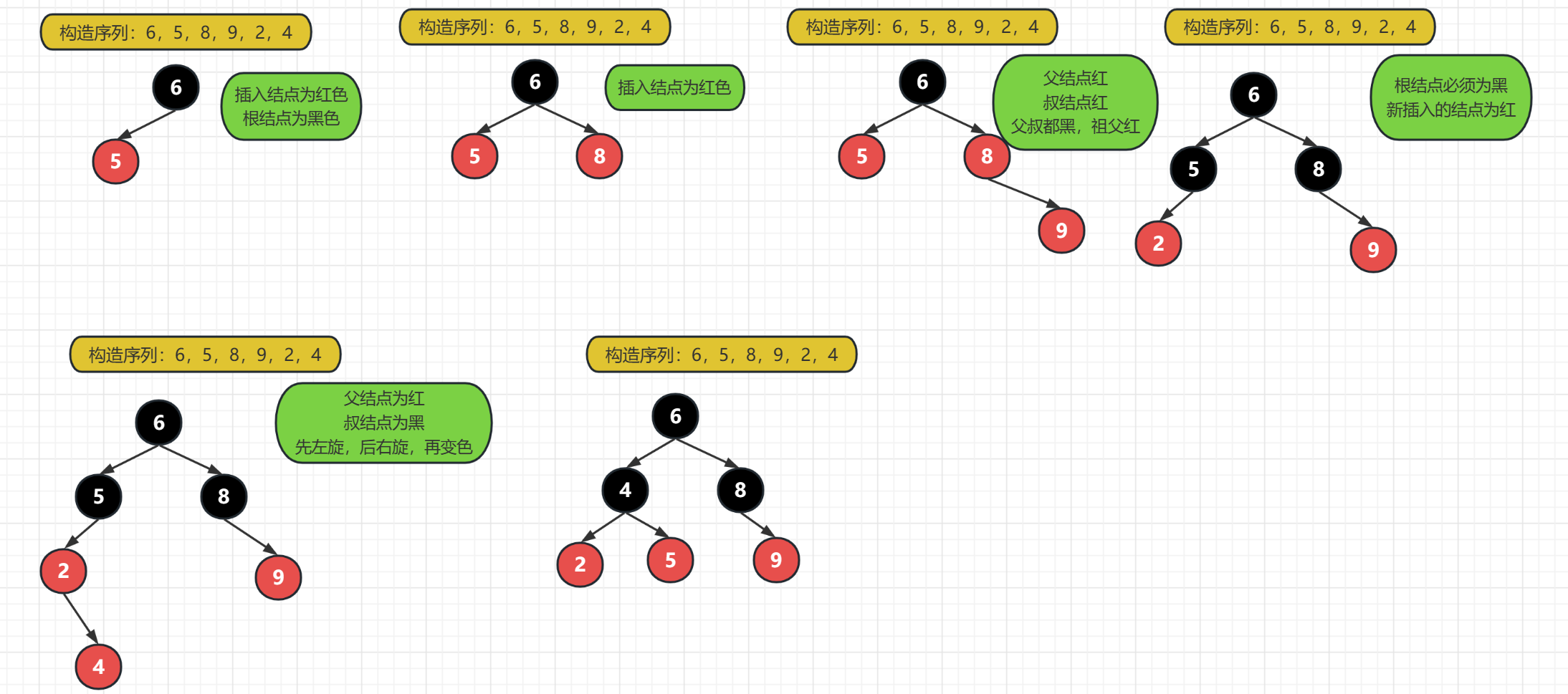
《資料結構與演演算法》之二元樹（補充樹）