【LeetCode專題#基本計算器】基本計算器I,圖解中序表示式轉逆波蘭表示式,太難了
基本計算器
https://leetcode.cn/problems/basic-calculator/?envType=list&envId=cKNEfNsF
給你一個字串表示式 s ,請你實現一個基本計算器來計算並返回它的值。
注意:不允許使用任何將字串作為數學表示式計算的內建函數,比如 eval() 。
範例 1:
輸入:s = "1 + 1"
輸出:2
範例 2:
輸入:s = " 2-1 + 2 "
輸出:3
範例 3:
輸入:s = "(1+(4+5+2)-3)+(6+8)"
輸出:23
提示:
1 <= s.length <= 3 * 105
s 由數位、'+'、'-'、'('、')'、和 ' ' 組成
s 表示一個有效的表示式
'+' 不能用作一元運算(例如, "+1" 和 "+(2 + 3)" 無效)
'-' 可以用作一元運算(即 "-1" 和 "-(2 + 3)" 是有效的)
輸入中不存在兩個連續的操作符
每個數位和執行的計算將適合於一個有符號的 32位元 整數
思路
本題由兩種方法解決,一種是單調棧,另一種是逆波蘭表示式(主要考慮逆波蘭)
使用逆波蘭表示式的話大概思路如下:
建立一個操作符棧op和一個結果棧res並將字串s(s為中序表示式)的第一個字元設定為當前字元
先將輸入的中序字串s中的空格處理掉,然後按以下規則從左到右依次遍歷中序字串s的每個字元
a. 如果當前字元是數位,則直接壓入結果棧中;
b. 如果當前字元是操作符,則分情況討論:
i. 如果當前操作符優先順序低於或等於操作符棧頂元素,則將操作符棧頂元素彈出並加入結果棧中,重複此步驟直到操作符棧為空或 者操作符的優先順序高於棧頂元素為止。然後將操作符壓入操作符棧中。
ii. 如果當前操作符優先順序高於操作符棧頂元素,則直接將操作符壓入操作符棧中。
c. 如果當前字元是左括號,則將其壓入操作符棧中。
d. 如果當前字元是右括號,則不斷地將操作符棧頂元素彈出並加入結果棧中,直到遇到左括號為止。
當中序表示式遍歷完畢後,如果操作符棧中還有剩餘元素,則將其全部彈出並加入結果棧中。 最後,結果棧中的元素就是逆波蘭表示式。
假設我們有中序表示式 "3 + 4 * (2 - 1)",現在來演示如何將其轉換為逆波蘭表示式:
首先先去空格,得到"3+4*(2-1)"
然後,建立操作符棧和結果棧,並將表示式的第一個字元 "3" 設定為當前字元。
接著,遍歷表示式中的下一個字元 "+":
因為 "+" 是一個操作符,所以將其與操作符棧頂元素比較。此時操作符棧為空,因此直接將 "+" 壓入操作符棧中。
下一個字元是數位 "4",因此將其直接壓入結果棧中。
下一個字元是操作符 "*",再次將其與操作符棧頂元素比較。因為 "*" 的優先順序高於 "+",所以直接將 "*" 壓入操作符棧中。
下一個字元是左括號 "(",將其壓入操作符棧中。
下一個字元是數位 "2",將其壓入結果棧中。
下一個字元是操作符 "-",將其壓入操作符棧中。
下一個字元是數位 "1",將其壓入結果棧中。
下一個字元是右括號 ")",此時需要不斷地將操作符棧頂元素彈出並加入結果棧中,直到遇到左括號為止。因此,彈出 "-"、"1" 和 "(" 並將它們依次加入結果棧中。
現在已經遍歷完了全部字元,但是操作符棧中還有剩餘元素"*"和"+",因此將其彈出並加入結果棧中。
最後,結果棧中
的元素就是逆波蘭表示式:"3421-*+"
這個逆波蘭表示式可以通過棧來求值。
圖解如下:
遍歷中序字串s,將操作符按優先順序壓入操作符棧op,將數位按遍歷順序(從左到右)壓入結果棧res

直到遇到右括號,這時,不斷遍歷操作符棧op,將操作符元素壓入結果棧res
直到遇到左括號結束
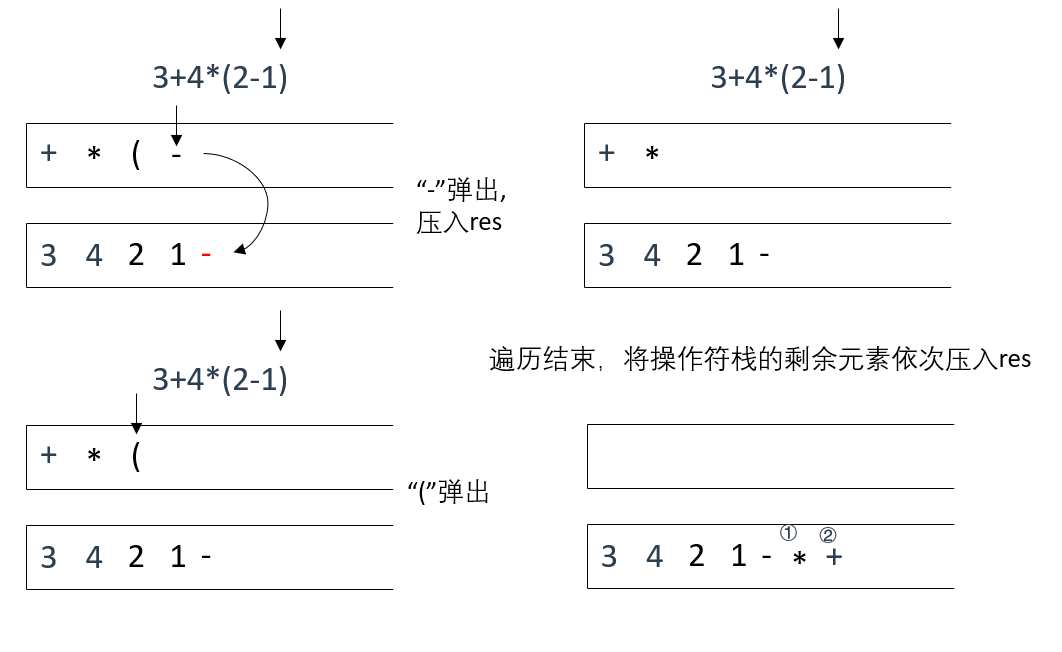
此時,如果op內還有剩餘操作符元素,將其依次彈出並加入res
得到結果"3421-*+"
逆波蘭表示式實現思路
程式碼實現中,我們需要寫四個函數:去除空格的函數removeBlack、逆波蘭表示式轉換函數toRPN、逆波蘭表示式求解函數getRes以及主函數calculate
class Solution {
private:
//有一個移除空格的函數
string removeBlack(string s){
string res = "";
for(char c : s){
if(c != ' ') res += c;
}
return res;
}
//將表示式分割為字尾表示式
void toRPN(string s){
...
}
//將表示式分割為字尾表示式
void getRes(){
...
}
public:
int calculate(string s) {
}
};
getRes()函數再計算逆波蘭表示式的結果時,需要一個vector
這裡還新增了一個priority函數用於返回操作符的優先順序
因此,toRPN的返回值應該是vector
class Solution {
private:
//有一個移除空格的函數
string removeBlack(string s){
string res = "";
for(char c : s){
if(c != ' ') res += c;
}
return res;
}
// 定義運運算元優先順序
int priority(char op) {
if (op == '+' || op == '-') return 1;
if (op == '*' || op == '/') return 2;
return 0;
}
//將中序表示式分割為字尾表示式
vector<string> toRPN(string s){
stack<string> op;//操作符棧
vector<string> res;//結果棧
string num = "";//記錄多位數位
for(char c : s){////遍歷當前輸入的中序字串s,判斷當前字元的型別
if(isdigit(c)){//當前字元c為數位
num += c;//為了防止當前數位有多位數,先用num收集
}else if(is_operator(c)){//當前字元c為操作符
if(!num.empty()){//證明num已經將數位收集完畢,壓入結果棧
res.push_back(num);
num = "";
}
//處理操作符邏輯,壓入op
//當前op中有操作符元素,比較兩者優先順序
//【如果op.top() == "("則說明現在之前遇到了")",現在正在彈出"("之前的所有操作符】
//以下情況表示棧頂運運算元的優先順序大於等於當前讀入的運運算元c的優先順序
while(!op.empty() && op.top() != "(" && priority(op.top()) >= priority(string(1, c))){
res.push_back(op.top());//將優先順序高的先壓入結果棧res
op.pop();//然後彈掉
}
op.push(string(1, c));//當前讀入的運運算元優先順序大於等於棧頂運運算元
}else if(c == '('){//當前字元c為左括號
if(!num.empty()){//證明num已經將數位收集完畢,壓入結果棧
res.push_back(num);
num = "";
}
op.push("(");
}else if(c == ')'){//當前字元c為右括號
if(!num.empty()){//證明num已經將數位收集完畢,壓入結果棧
res.push_back(num);
num = "";
}
while(op.top() != "(" && !op.empty()){//不斷彈出操作符棧頂元素加入到結果棧res中
res.push_back(op.top());
op.pop();
}
op.pop();//多彈一次取出左括號
}
}//遍歷處理完畢,如果num和操作符棧還有剩的元素,先將num壓入res再壓op
if(!num.empty()){//如果還有數位未入結果棧,則加入
res.push_back(num);
}
while(!op.empty()){//將剩餘的操作符入結果棧
res.push_back(op.top());
op.pop();
}
return res;
}
//計算逆波蘭表示式,LeetCode.150
int getRes(vector<string>& tokens){
}
public:
int calculate(string s) {
}
};
第一版程式碼
基於LeetCode.150的知識補充完getRes函數後我們得到了第一版程式碼,是不是很爽?範例用例都ac
class Solution {
private:
//有一個移除空格的函數 //只是將原字串的空格去除後,生成了一個新的字串,但並沒有將原字串進行修改,錯誤
string removeBlack(string& s){
string res = "";
for(char c : s){
if(c != ' ') res += c;
}
return res;
}
// 定義運運算元優先順序
int priority(string op) {
if (op == "+" || op == "-") return 1;
if (op == "*" || op == "/") return 2;
return 0;
}
bool is_operator(char c) {//判斷當前元素是否為操作符
switch(c) {
case '+':
case '-':
case '*':
case '/':
return true;
default:
return false;
}
}
//將中序表示式分割為字尾表示式
vector<string> toRPN(string s){
stack<string> op;//操作符棧
vector<string> res;//結果棧
string num = "";//記錄多位數位
for(char c : s){////遍歷當前輸入的中序字串s,判斷當前字元的型別
if(isdigit(c)){//當前字元c為數位
num += c;//為了防止當前數位有多位數,先用num收集
}else if(is_operator(c)){//當前字元c為操作符
if(!num.empty()){//證明num已經將數位收集完畢,壓入結果棧
res.push_back(num);
num = "";
}
//處理操作符邏輯,壓入op
//當前op中有操作符元素,比較兩者優先順序
//【如果op.top() == "("則說明現在之前遇到了")",現在正在彈出"("之前的所有操作符】
//以下情況表示棧頂運運算元的優先順序大於等於當前讀入的運運算元c的優先順序
while(!op.empty() && op.top() != "(" && priority(op.top()) >= priority(string(1, c))){
res.push_back(op.top());//將優先順序高的先壓入結果棧res
op.pop();//然後彈掉
}
op.push(string(1, c));//當前讀入的運運算元優先順序大於等於棧頂運運算元
}else if(c == '('){//當前字元c為左括號
if(!num.empty()){//證明num已經將數位收集完畢,壓入結果棧
res.push_back(num);
num = "";
}
op.push("(");
}else if(c == ')'){//當前字元c為右括號
if(!num.empty()){//證明num已經將數位收集完畢,壓入結果棧
res.push_back(num);
num = "";
}
while(op.top() != "(" && !op.empty()){//不斷彈出操作符棧頂元素加入到結果棧res中
res.push_back(op.top());
op.pop();
}
op.pop();//多彈一次取出左括號
}
}//遍歷處理完畢,如果num和操作符棧還有剩的元素,先將num壓入res再壓op
if(!num.empty()){//如果還有數位未入結果棧,則加入
res.push_back(num);
}
while(!op.empty()){//將剩餘的操作符入結果棧
res.push_back(op.top());
op.pop();
}
return res;
}
//計算逆波蘭表示式,LeetCode.150
int getRes(vector<string>& tokens){
stack<long long> st;
//遍歷字串
for(int i = 0; i < tokens.size(); ++i){
if(tokens[i] == "+"|| tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){//遇到運運算元
//取兩個數
long long num1 = st.top();
st.pop();
long long num2 = st.top();
st.pop();
//判斷運運算元,做相應計算並壓棧//注意計算順序,num2[運運算元]num1
if(tokens[i] == "+") st.push(num2 + num1);
if(tokens[i] == "-") st.push(num2 - num1);
if(tokens[i] == "*") st.push(num2 * num1);
if(tokens[i] == "/") st.push(num2 / num1);
}else{//遇到數位
//轉為整型,壓棧
st.push(stoll(tokens[i]));
}
}
int res = st.top();
st.pop();//記憶體回收
return res;
}
public:
int calculate(string s) {
string noBlackIn_s = removeBlack(s);
vector<string> rpn4s = toRPN(noBlackIn_s);
return getRes(rpn4s);
}
};
坑
但是,上述程式碼在測試用例為"1-( -2)"時報錯了(咬牙切齒)
Line 171: Char 16: runtime error: reference binding to misaligned address 0xbebebebebebec0b6 for type 'long long', which requires 8 byte alignment (stl_deque.h)
0xbebebebebebec0b6: note: pointer points here
<memory cannot be printed>
SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior /usr/bin/../lib/gcc/x86_64-linux-gnu/9/../../../../include/c++/9/bits/stl_deque.h:180:16
原因大概是因為按照我們之前的邏輯寫的toRPN函數沒有考慮到有負數的情況。。。
怎麼辦,改唄
第二版程式碼
考慮了負號,但是測試用例仍然只通過24/44
class Solution {
private:
string removeBlack(string& s){
string res = "";
int i = 0, n = s.size();
while(i < n){
if(s[i] == ' ') ++i;
else if(s[i] == '-'){
// 跳過空格
while(i < n && s[i] == ' ') ++i;
// 判斷減號前是否有數位或左括號
if(i == 0 || s[i-1] == '('){
res += '0';
}
// 將減號複製到新字串中
res += '-';
++i;
// 將減號後面的數位複製到新字串中
while(i < n && isdigit(s[i])){
res += s[i];
++i;
}
// 在數位後面新增空格,以便後續處理
res += ' ';
}else{
// 複製其他字元到新字串中
res += s[i];
++i;
}
}
return res;
}
int priority(string op) {
if (op == "+" || op == "-") return 1;
if (op == "*" || op == "/") return 2;
return 0;
}
bool is_operator(char c) {
switch(c) {
case '+':
case '-':
case '*':
case '/':
return true;
default:
return false;
}
}
vector<string> toRPN(string s){
stack<string> op;
vector<string> res;
string num = "";
for(int i = 0; i < s.size(); ++i){
char c = s[i];
if(isdigit(c)){
num += c;
}else if(is_operator(c)){
if(!num.empty()){
res.push_back(num);
num = "";
}
while(!op.empty() && op.top() != "(" && priority(op.top()) >= priority(string(1, c))){
res.push_back(op.top());
op.pop();
}
op.push(string(1, c));
}else if(c == '('){
if(!num.empty()){
res.push_back(num);
num = "";
}
op.push("(");
}else if(c == ')'){
if(!num.empty()){
res.push_back(num);
num = "";
}
while(op.top() != "(" && !op.empty()){
res.push_back(op.top());
op.pop();
}
op.pop();
}else if(c == ' '){ // 處理空格
if(!num.empty()){
res.push_back(num);
num = "";
}
// 如果前一個字元不是減號,則將空格新增到新字串中
if(i > 0 && s[i-1] != '-'){
res.push_back(" ");
}
}
}
if(!num.empty()){
res.push_back(num);
}
while(!op.empty()){
res.push_back(op.top());
op.pop();
}
return res;
}
int getRes(vector<string>& tokens){
stack<int> st;
for(int i = 0; i < tokens.size(); ++i){
if(tokens[i] == "+"|| tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){
int num1 = st.top();
st.pop();
int num2 = st.top();
st.pop();
if(tokens[i] == "+") st.push(num2 + num1);
if(tokens[i] == "-") st.push(num2 - num1);
if(tokens[i] == "*") st.push(num2 * num1);
if(tokens[i] == "/") st.push(num2 / num1);
}else{
// st.push(stoi(tokens[i]));
stringstream ss(tokens[i]);
int num;
ss >> num;
st.push(num);
}
}
int res = st.top();
st.pop();
return res;
}
public:
int calculate(string s) {
string noBlackIn_s = removeBlack(s);
vector<string> rpn4s = toRPN(noBlackIn_s);
return getRes(rpn4s);
}
};
放棄逆波蘭表示式的寫法了
改用棧吧,下面貼一個論壇老哥的解法的分析,我修不動原來的程式碼了
class Solution {
public:
// 去除空格
string removeBlank(string s) {
string res = "";
for(char c:s) {
if(c!=' ') res += c;
}
return res;
}
// 將中綴表示式轉化為字尾表示式
queue<string> getToken(string s) {
s = removeBlank(s);
string push_src = "";
queue<string> res;
bool pre = true;
for(char c:s) {
//判斷是不是單目運運算元 使用$代替單目運運算元
if(c == '-' && pre) {
if(push_src!="") {
res.push(push_src);
push_src = "";
}
res.push("$");
}else if(c == '+' || c=='-' || c=='*' || c=='/' || c=='(' || c==')'||c=='#') {
if(c!=')')pre = true;
if(push_src!="") {
res.push(push_src);
push_src = "";
}
res.push(string("")+c);
}else{
pre = false;
push_src += c;
}
}
if(push_src!="") {
res.push(push_src);
push_src = "";
}
return res;
}
// 給定一個字尾表示式,求其值
int calculate(string s) {
queue<string> in = getToken(s+"#"); // #表示計算結束
map<string,int> isp = {
{"#",0},{"(",1},{"*",5},{"/",5},{"+",3},{"-",3},{")",8},{"$",7}
};
map<string,int> icp = {
{"#",0},{"(",8},{"*",4},{"/",4},{"+",2},{"-",2},{")",1},{"$",6}
};
queue<string> out; // 儲存字尾表示式
stack<string> stk; // 操作符棧
stk.push("#");
string ch = in.front(); // 取隊首元素
in.pop();
while(stk.top()!="#"||ch!="#") { // 當操作符棧為空且佇列已經空了之後才結束迴圈
if(isp.find(ch)==isp.end()) { // 判斷是否為數位,不是則直接加入字尾表示式
out.push(ch);
ch = in.front();
in.pop();
continue;
}
if(icp[ch] > isp[stk.top()]) { // 操作符優先順序較低則直接加入棧中
stk.push(ch);
ch = in.front();
in.pop();
}else if(icp[ch] < isp[stk.top()]) { // 操作符優先順序較高則彈出棧頂操作符加入字尾表示式
out.push(stk.top());
stk.pop();
}else { // 相等則彈出棧頂的左括號或右括號
stk.pop();
if(ch!="#") {
ch = in.front();
in.pop();
}
}
}
stack<int> sk;// 儲存數位的棧
//TODO:逆波蘭式子求解
while(!out.empty()) {// 遍歷字尾表示式求值
string cur = out.front();
out.pop();
if(cur == "$") {// 處理單目運運算元
int a = sk.top();
sk.pop();
sk.push(-a);
}else if(cur == "+") {
int a2 = sk.top();
sk.pop();
int a1 = sk.top();
sk.pop();
sk.push(a1+a2);
}else if(cur == "-") {
int a2 = sk.top();
sk.pop();
int a1 = sk.top();
sk.pop();
sk.push(a1-a2);
}else if(cur == "*") {
int a2 = sk.top();
sk.pop();
int a1 = sk.top();
sk.pop();
sk.push(a1*a2);
}else if(cur == "/") {
int a2 = sk.top();
sk.pop();
int a1 = sk.top();
sk.pop();
sk.push(a1/a2);
}else {
sk.push(stoi(cur));
}
}
return sk.top();
}
};
上述程式碼實現的是一個基本的四則運算計算器,其核心思路是將中綴表示式轉化為字尾表示式,再根據字尾表示式求值得到結果。這個過程可以概括為:(GPT生成)
- 初始化兩個棧,一個操作符棧stk和一個數位棧sk,初始化一個佇列out用來儲存字尾表示式;
- 遍歷中綴表示式,對於每個字元進行如下判斷:
- 如果是數位,直接入隊out;
- 如果是左括號,入棧stk;
- 如果是右括號,彈出操作符棧中的元素並加入佇列out,直到遇到左括號;注意:左右括號都不入隊out;
- 如果是操作符,則判斷其與操作符棧頂元素的優先順序關係,如果優先順序高,則壓入操作符棧,否則將操作符棧中的元素彈出,加入佇列out,然後繼續比較棧頂元素和當前操作符的優先順序,直至當前操作符可以入棧;
- 當遍歷完中綴表示式後,如果操作符棧中還有元素,則將其全部依次彈出,並加入佇列out;
- 此時out中儲存的就是字尾表示式,對其進行求值即可得到結果。
例如,對於中綴表示式"3+42/(1-5)#",按照上述演演算法可得到字尾表示式"34215-/+"。具體過程如下:
- 初始化操作符棧和佇列out,將中綴表示式轉化為一個字元陣列arr;
- 從左到右遍歷arr,對於每個元素進行判斷:
- 當前元素是數位,直接加入out中;
- 當前元素是'(',壓入操作符棧中;
- 當前元素是')',彈出操作符棧中的元素並加入out,直至遇到'(';
- 當前元素是運運算元,比較其與操作符棧頂元素的優先順序,如果優先順序高,則將其壓入操作符棧;否則,依次彈出操作符棧中的元素並加入out,直至當前運運算元可以入棧;
- 遍歷完arr後,將操作符棧中的剩餘元素全部彈出,並加入out;
- 對out中的元素進行求值,得到最終結果11。
在程式碼的 removeBlank 函數中,採用了一個簡單的遍歷字串的方式來去除空格。具體來說,將原字串中非空格的字元依次加入一個新的字串中即可。
在處理單目運運算元時,則需要考慮到單目運運算元和減號(二元運運算元)的區別。我們可以通過一個 bool 變數 pre 來判斷當前字元是否為單目運運算元。具體來說,如果 pre 為 true,且當前字元為減號,則說明其為單目運運算元;否則,當前字元為減號則表示其為二元操作符。當遇到單目運運算元時,我們可以將其替換為 "$",在後面進行求值時再做特殊處理即可。
另外,在這個函數中還使用了一個輔助變數 push_src 來儲存當前正在處理的數位串。當遇到運運算元或者結束符號 # 時,就將該數位串加入佇列 res 中。同時,pre 的取值根據當前字元是不是右括號進行相應的修改。
括號展開+棧
這個是LeetCode的官方解法
class Solution {
public:
int calculate(string s) {
stack<int> ops; // 用於儲存括號內的符號
ops.push(1); // 先將符號入棧,初始為1
int sign = 1; // 當前數位的符號,預設為正數
int ret = 0; // 最終結果
int n = s.length(); // 字串長度
int i = 0; // 當前遍歷到字串中的位置
while (i < n) {
if (s[i] == ' ') { // 空格直接跳過
i++;
} else if (s[i] == '+') { // 遇到加號,更新符號為棧頂的符號
sign = ops.top();
i++;
} else if (s[i] == '-') { // 遇到減號,更新符號為棧頂的符號的相反數
sign = -ops.top();
i++;
} else if (s[i] == '(') { // 遇到左括號,將當前符號入棧
ops.push(sign);
i++;
} else if (s[i] == ')') { // 遇到右括號,彈出棧頂符號
ops.pop();
i++;
} else { // 遇到數位,計算出完整的數位,並與當前符號相乘後累加到最終結果
long num = 0;
while (i < n && s[i] >= '0' && s[i] <= '9') {
num = num * 10 + s[i] - '0';
i++;
}
ret += sign * num;
}
}
return ret; // 返回最終結果
}
};
上述程式碼基於棧的思想實現了對帶有括號的數學表示式的計算。其核心思路如下:
1.使用一個操作符棧 ops 儲存括號內的符號,初始時將 1 入棧表示整個表示式的符號為正號。
2.遍歷表示式中的每個字元,分別處理以下幾種情況:
如果遇到空格,直接跳過。
如果遇到加號 +,則更新當前符號為棧頂的符號,並繼續向後遍歷。
如果遇到減號 -,則更新當前符號為棧頂的符號的相反數,並繼續向後遍歷。
如果遇到左括號 (,則將當前符號入棧,並繼續向後遍歷。
如果遇到右括號 ),則彈出棧頂符號,並繼續向後遍歷。
如果遇到數位,則計算出完整的數位,並與當前符號相乘後累加到最終結果,並繼續向後遍歷。
3.最終返回最終結果即可。
這樣的實現可以處理帶有括號的複雜表示式,同時也考慮到了符號的影響。
舉一個例子,計算表示式 "1 + (2 - 3) - 4"
首先初始化操作符棧 ops,將符號 1 入棧:ops: [1]
然後從左到右遍歷表示式中的每個字元,依次進行處理:
遇到數位 1,累加到最終結果 ret 中,此時 ret=1。
遇到空格,直接跳過。
遇到加號 +,更新當前符號為 ops 棧頂的符號 1,此時 sign=1,繼續向後遍歷。
遇到左括號 (,將當前符號 sign=1 入棧,此時 ops: [1, 1],繼續向後遍歷。
遇到數位 2,由於此時棧頂符號為正號,所以累加到最終結果 ret 中,此時 ret=3。
遇到減號 -,更新當前符號為棧頂的符號的相反數 -1,此時 sign=-1,繼續向後遍歷。
遇到數位 3,由於此時棧頂符號為負號,所以將其乘以 (-1) 並累加到最終結果 ret 中,此時 ret=2。
遇到右括號 ),彈出棧頂符號,並繼續向後遍歷,此時 ops: [1]。
遇到減號 -,更新當前符號為棧頂的符號的相反數 -1,此時 sign=-1,繼續向後遍歷。
遇到數位 4,由於此時棧頂符號為負號,所以將其乘以 (-1) 並累加到最終結果 ret 中,此時 ret=-3。
最終返回結果 ret=-3