曲線藝術程式設計 coding curves 第九章 旋輪曲線(ROULETTE CURVES)
第九章 旋輪曲線(ROULETTE CURVES)
原作:Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/
譯者:池中物王二狗(sheldon)
原始碼:github: https://github.com/willian12345/coding-curves
曲線藝術程式設計系列第 9 章
一開始我本章標題我打算使用「次擺線與擺線(旋輪線)」。我想它們是兩種不同型別的曲線,雖然有點兒聯絡。但隨著瞭解的深入,我有點兒凌亂了。事實上擺線是一類非常特別的次擺線。我會原諒我自己的。這是維基百科上它們的定義:
在幾何上,次擺線(trochoid 原自古希臘語 trochos ‘wheel’)是一個圓延一條直線捲動一圈形成的旋轉曲線。
在幾何上, 擺線追蹤在圓上的一個點,圓延直線捲動後形成的曲線。
它們不僅不是兩個不同的東西,從描述上看它們幾乎是同一個東西。細節決定成敗。讓我們開始探索吧。
有三種不同的次擺線:
- 普通次擺線(也稱擺線)
- Prolate trochoids 長幅擺線
- Curtate trochoids 短幅擺線
除此之外,還有一些相關的曲線,大概覆蓋以下幾種:
Epitrochoids 長短輻外擺線
Hypotrochoids 長短輻內擺線
Epicycloids 外擺線
Hypocycloids 內擺線
Involutes 漸伸線
它們組合在一起就是旋輪曲線家族了。在這章除 Involutes 漸伸線外其它都將涉及到。
講了了大堆有的沒的,先從次擺線開始,讓我們一一把它們搞清楚。
Trochoids 次擺線
就像上面描述的,一條次擺線就是一個圓在直線上捲動形成的旋轉曲線。在編碼之前先把它視覺化看看:
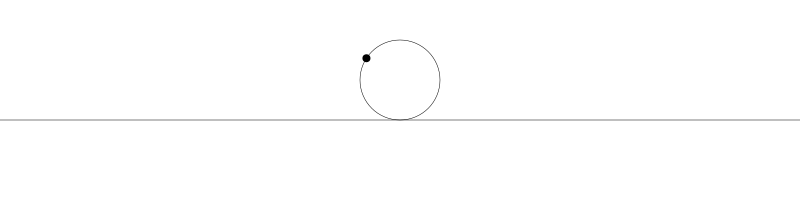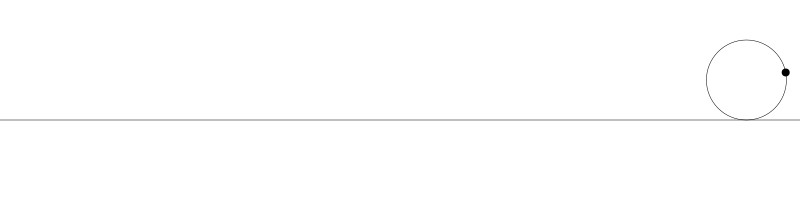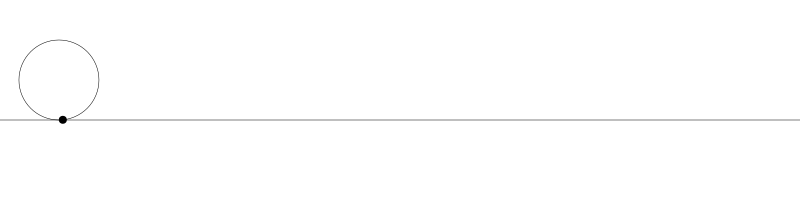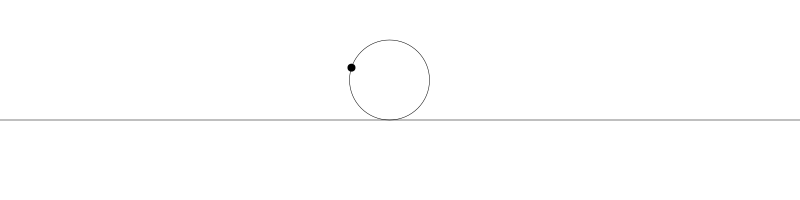
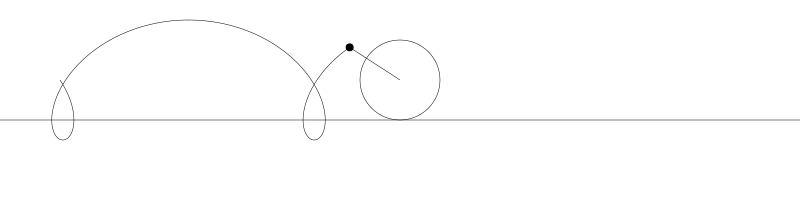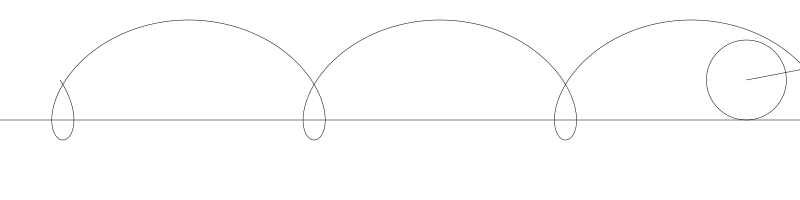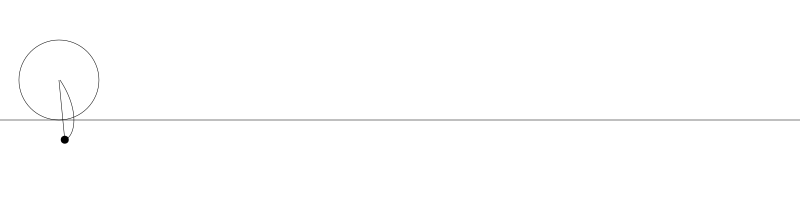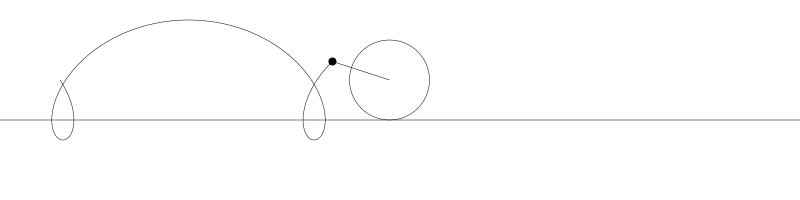
如果我們追蹤圓周上的那個黑點...
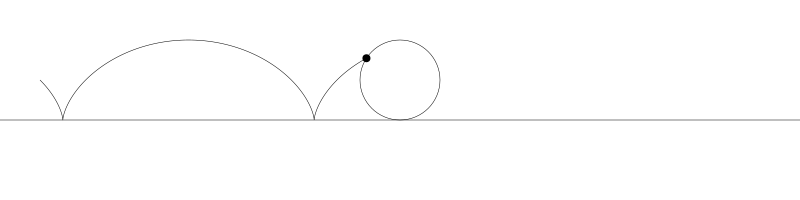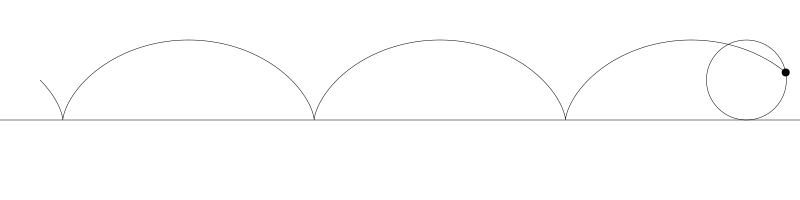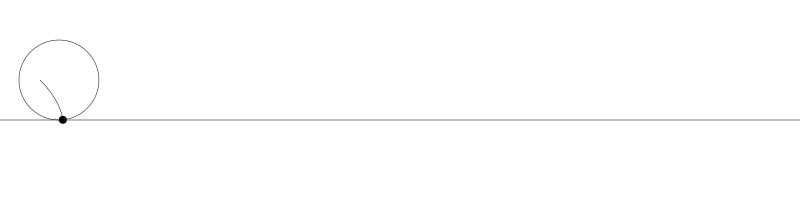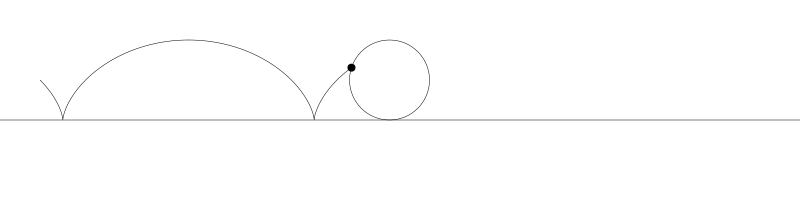
... 新的曲線就是次擺線。事實上由於是繪製點依賴於圓周,所以也稱為普通擺線或圓滾線。
如果將圓周上的點延伸超過圓周,那麼我們就得到長幅次擺線(Prolate trochoid)。
如果黑點在圓內部,它就是短幅次擺線(Curtate trochoids)。
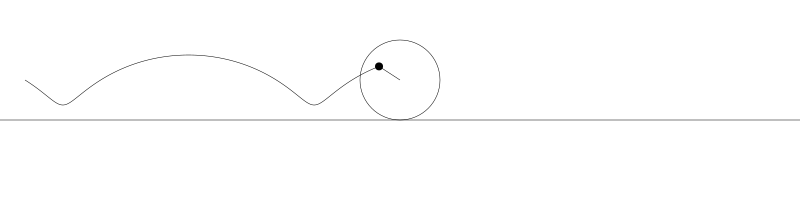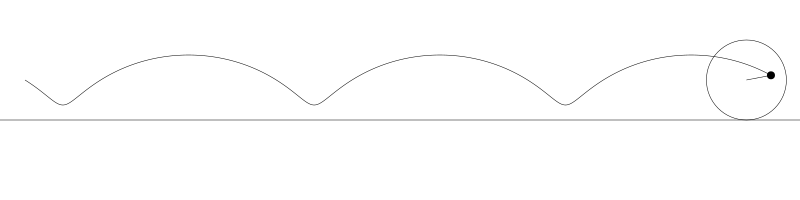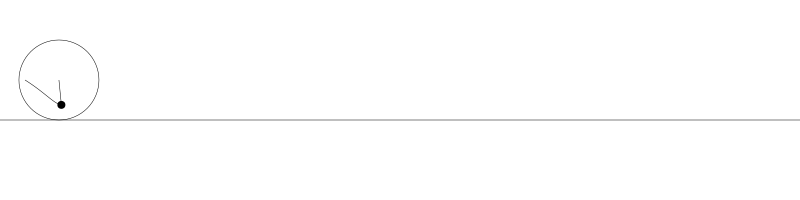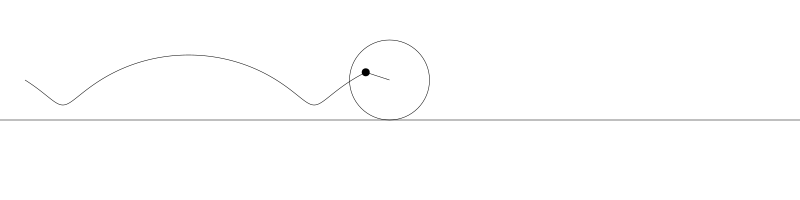
為了做出這些動畫,我讓圓從左向右運動,計算出每個位置上圓的旋轉角度,用 sine 和 cosine 基於圓的位置與旋轉角度計算出點的位置,然後用這些點畫出線。但對於次擺線其實有更直接的公式
x = a * t - b * sin(t)
y = a - b * cos(t)
t 是圓的旋轉角度,它可以無限增長, a 是圓的半徑, b 是圓心點至繪製點的距離 - 可以說是那個點的半徑。讓我們把它實現出來:
width = 800
height = 300
canvas(width, height)
translate(0, height/2)
scale(1, -1)
moveTo(0, 0)
lineTo(width, 0)
stroke()
a = 20.0
b = 20.0
res = 0.05
for (t = 0.0; t < width; t += res) {
x = a * t - b * sin(t)
y = a - b * cos(t)
lineTo(x, y)
}
stroke()
公式是基於笛卡爾座標的,我們要將 y 軸移至 canvas 中心,並將 y 軸翻轉。
然後畫一條直線從 y 軸中心穿過用於表示圓捲動時的「地面」。你可以畫也可以選擇不畫。
我們將 a 和 b 都設為 20, 這樣就可以得到擺線(譯者者:普通旋轉線)了。我們迴圈將從 0 至 canvas 的寬度用於變數 t, 應用公式連線至計算出的結果點。
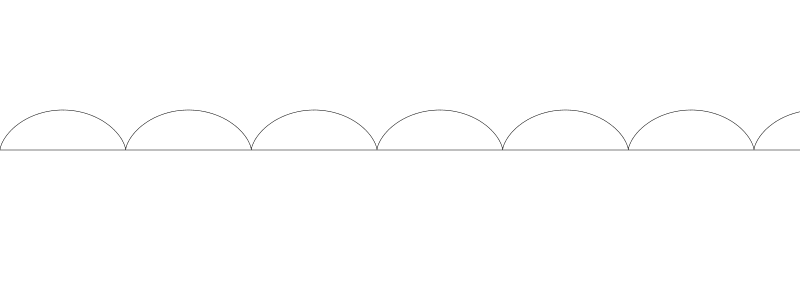
如果將 b 提高到 60, 我們就得到了長幅擺線
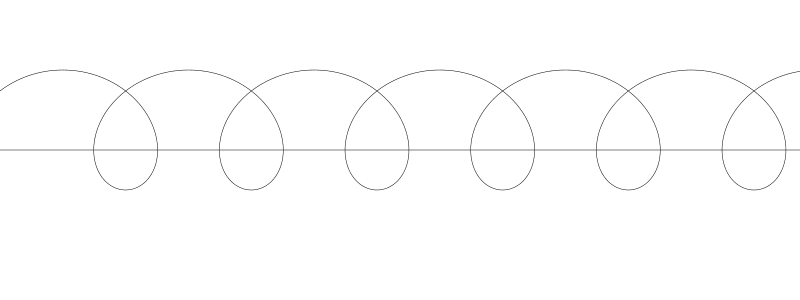
如果將 b 減小到 10, 我們就得到了短幅擺線。
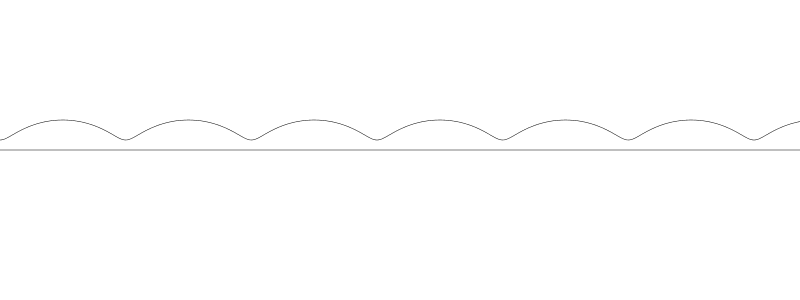
我不知道長幅擺線和短幅擺線的用詞是否準確,但聽起來挺酷。
這就是全部關於次擺線的內容。試試給 a 和 b 設不同的值,或者你自己改一下其它值,我就不再再多講了。因為下面還留有很多旋輪曲線需要探討。
中心次擺線
接下來我們要聚焦於被稱為中心次擺線的四種曲線。與延直線捲動不同,它是延另一個圓捲動,可能是延那個圓圓內部捲動也可能是延那個圓的外部捲動。
四類分別是:
- Epicycloids 外擺線 - 延一個圓外部捲動的圓,圓周上某一點軌跡形成的曲線。
- Epitrochoids 長短輻外擺線 - 與上面一個一樣,但這個點是不在圓周上,而是在圓外或圓內,與短幅次擺線與長幅次擺線一樣。
- Hypocycloids 內擺線 - 延一個圓內部捲動的圓,圓周上某一點軌跡形成的曲線。
- Hypotrochoids 長短輻內擺線 - 與上面那個一樣,但這個點是不在圓周上,而是在圓外或圓內
除此之外,還有一些曲線也是屬於上面曲線的一種變體,只是形成曲線的兩個圓半徑有特殊的比例關係。我們稍後會看介紹一些。
Epitrochoids 長短輻外擺線
首先,讓我們將一個圓延另一個圓外捲動視覺化
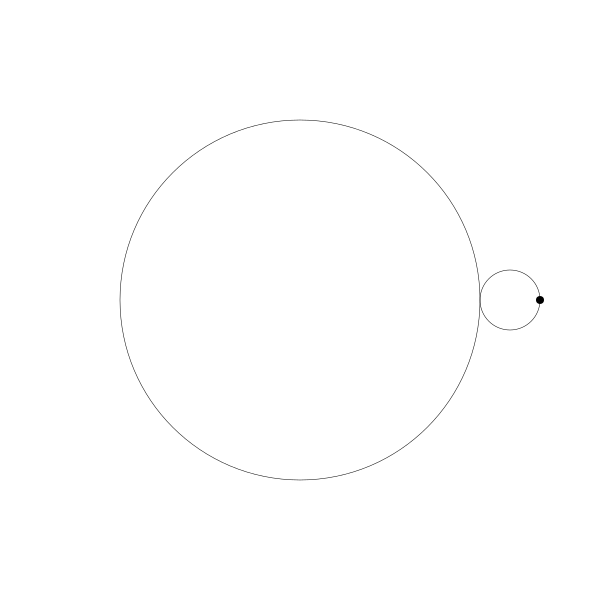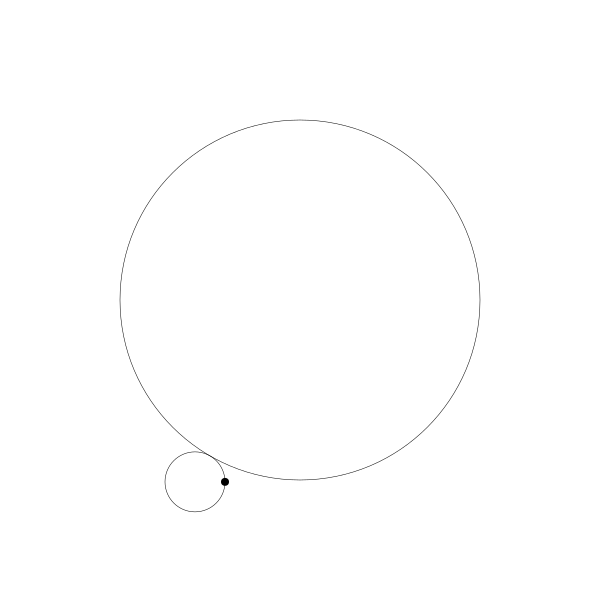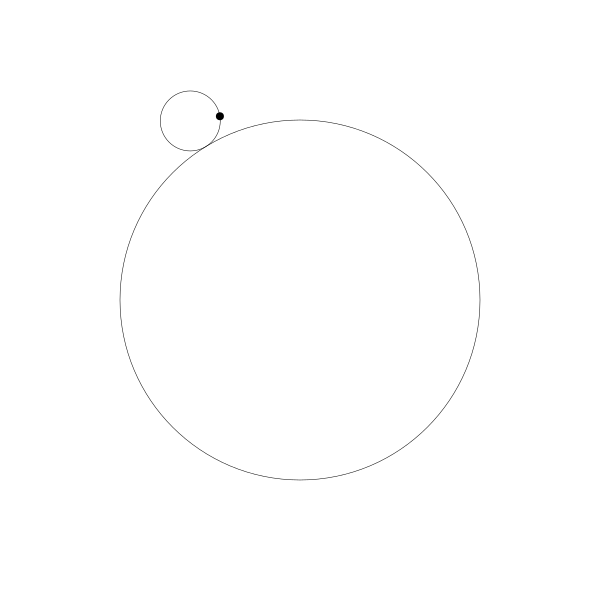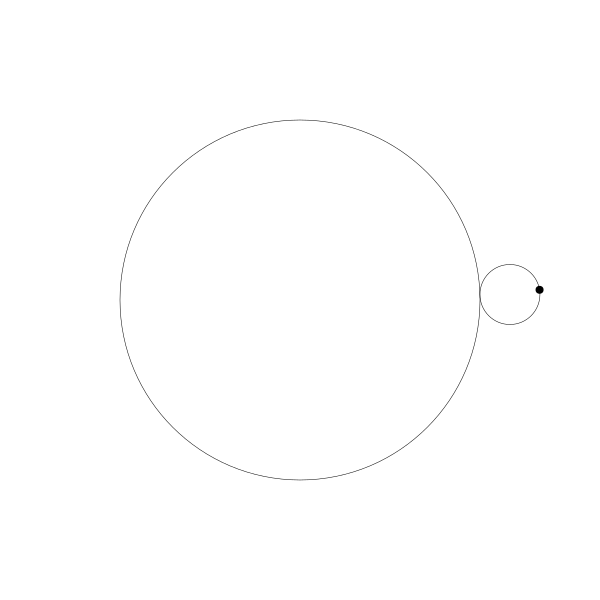
再追蹤一下那個黑色的點的繪製結果
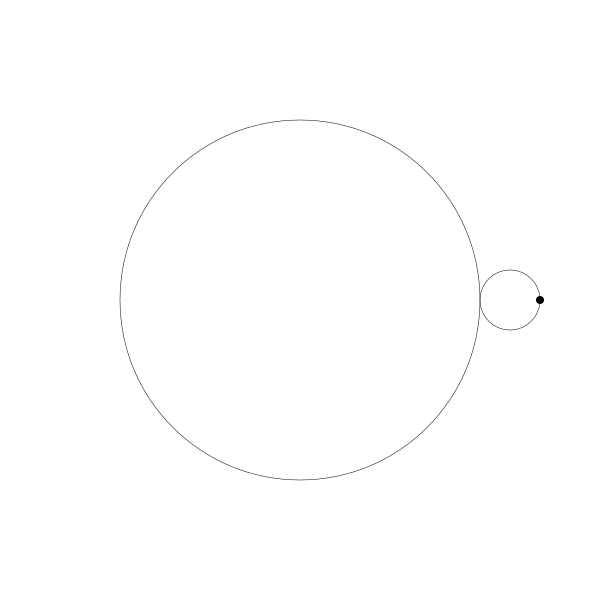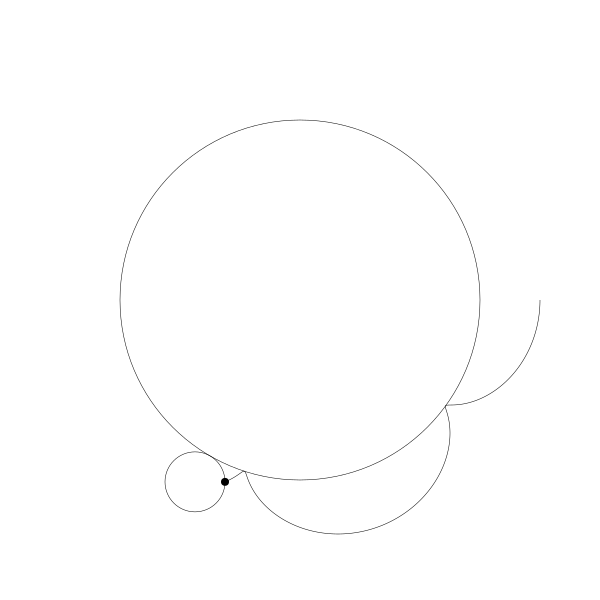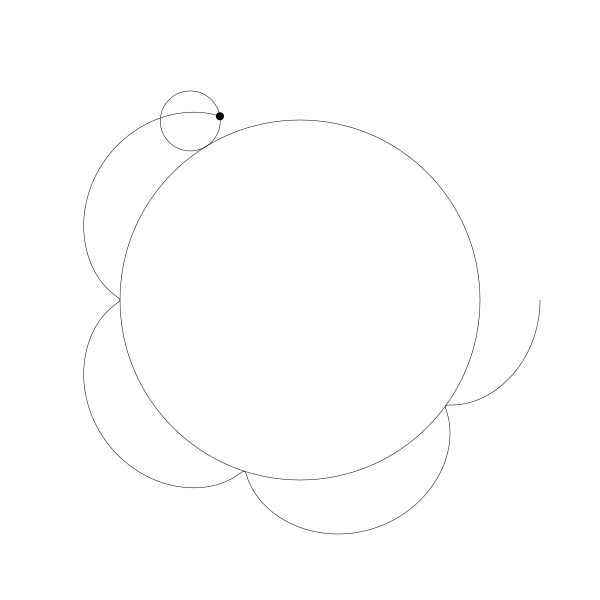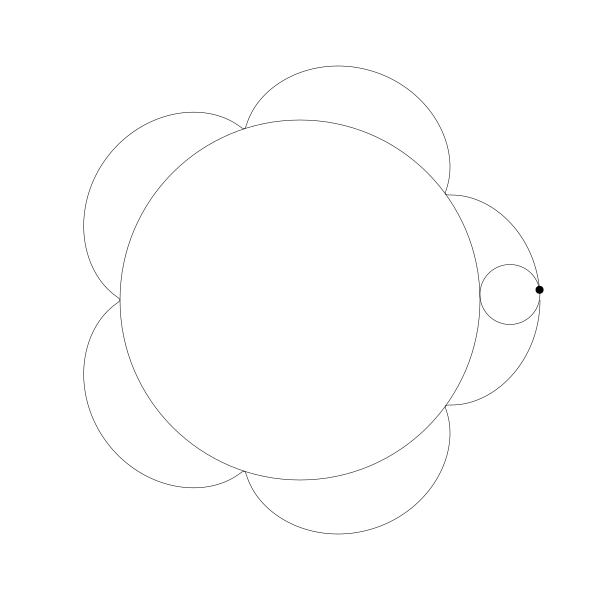
這就是你長短輻外擺線!
事實上,由於那個點是在圓周位置上,所以這也就是外擺線!
如果將點往外移動一點...

再我們往內移動一點。
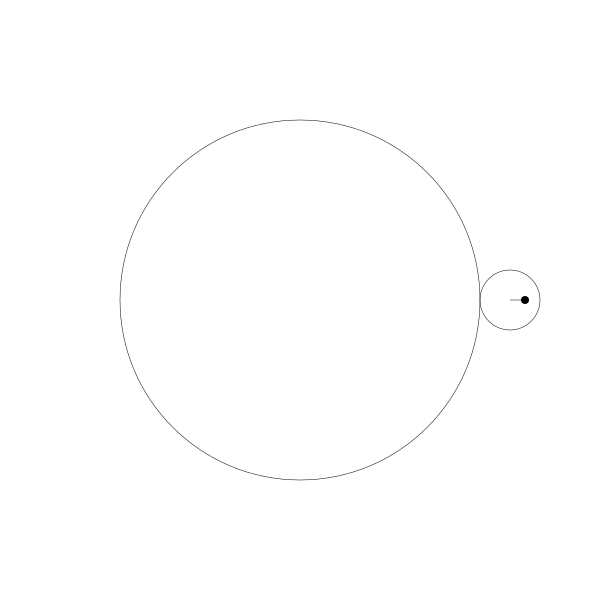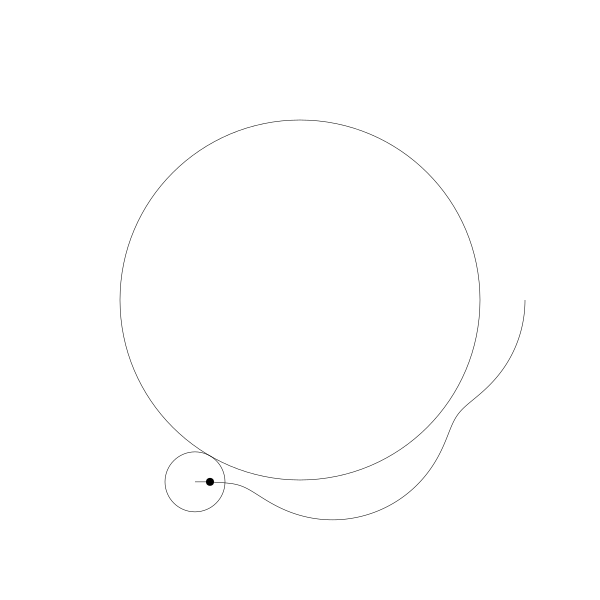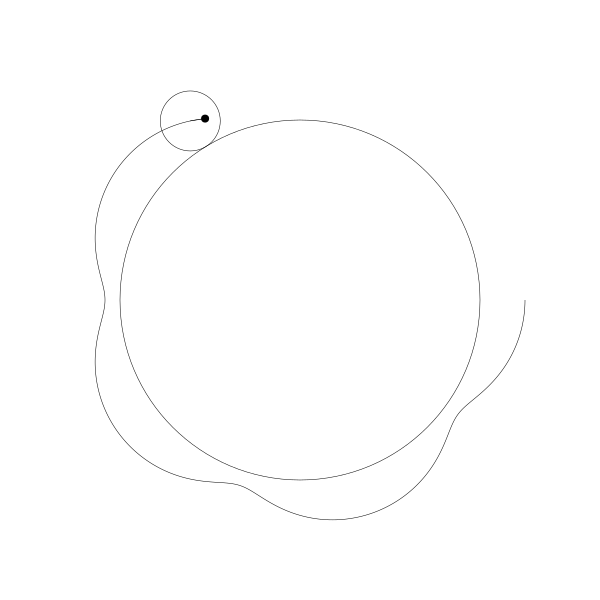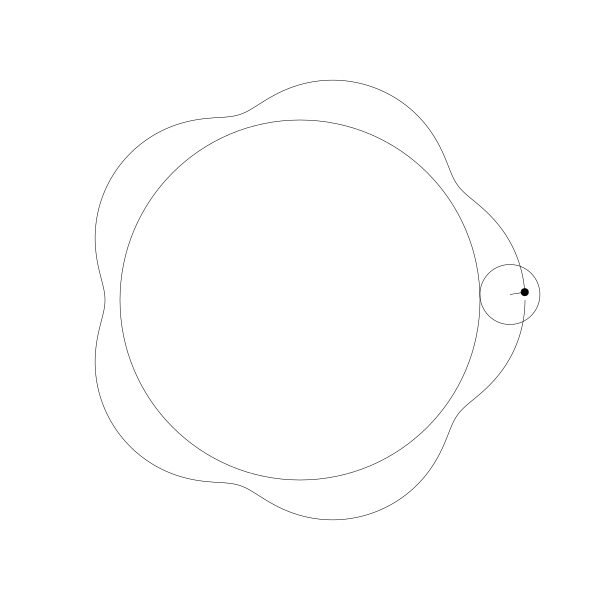
再一次,我建立這些動畫是通過計算這些圓的位置,繪製這些圓,再計算這些圓的旋轉角度並繪製對應的點, 然後再連線每一幀所繪製的點路徑形成曲線。為了展示動畫像這麼做是值得的,但是其實是有更簡單的公式,你可以直接應用:
長短輻外擺線公式:
x = (r0 + r1) * cos(t) - d * cos(((r0 + r1) * t) / r1)
y = (r0 + r1) * sin(t) - d * sin(((r0 + r1) * t) / r1)
引數解析:
- r0 是定圓的半徑
- r1 是動圓的半徑
- t 是增長的弧度
- d 是動圓中心點與繪製點之間的距離 (如果是外擺線則 r1 與 d 相同)
我們用這個公式瞬間就可以用些程式碼實現:
width = 800
height = 800
canvas(width, height)
translate(width/2, height/2)
r0 = 180
r1 = 60
d = 60
res = 0.01
circle(0, 0, r0)
stroke()
for (t = 0.0; t < PI * 2; t += res) {
x = (r0 + r1) * cos(t) - d * cos(((r0 + r1) * t) / r1)
y = (r0 + r1) * sin(t) - d * sin(((r0 + r1) * t) / r1)
lineTo(x, y)
}
stroke()
我們設定變數 r0, r1, d 然後繪製定圓僅僅是為了參照變數
接著迴圈 t 至 2 * PI, 得到 x, y 點,繪製一條線至那個點。
得到結果:

值得注意的一點, ro 到 r1 的比例。 180:60 或 3:1。 我們得到3個結點。如果將 r1 改為 45,比例即變為 4:1 , 我們將得到 4 個結點。(我將 d 變為 45 也是為了適配 r1)
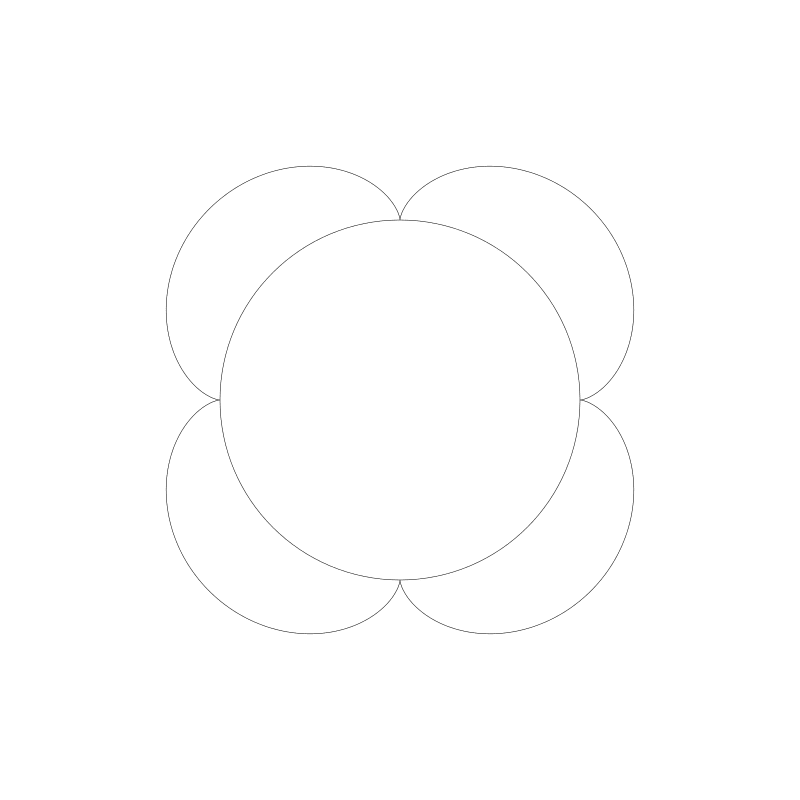
下面是 12:1 :
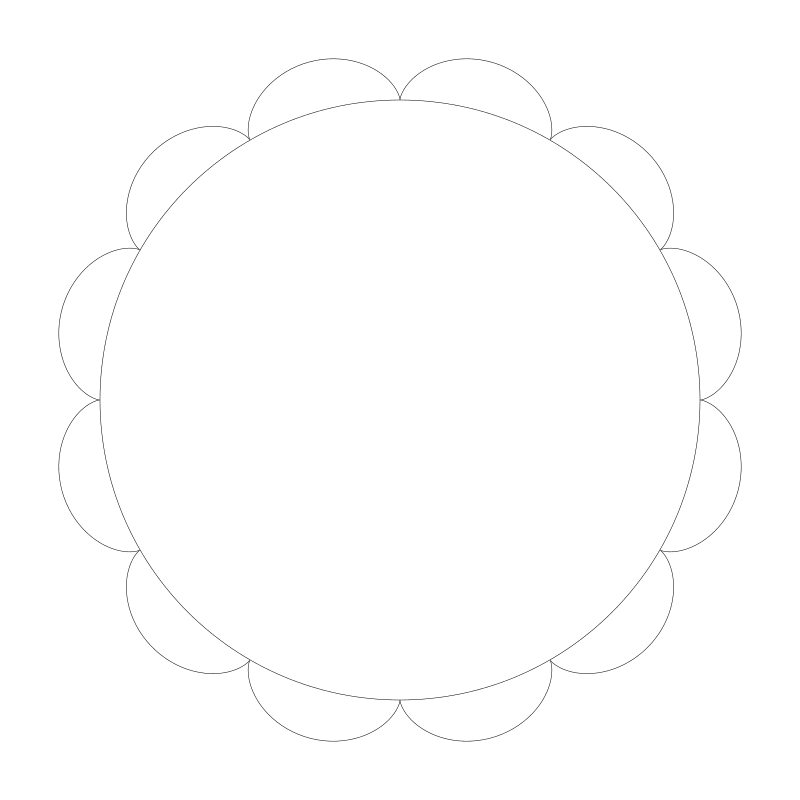
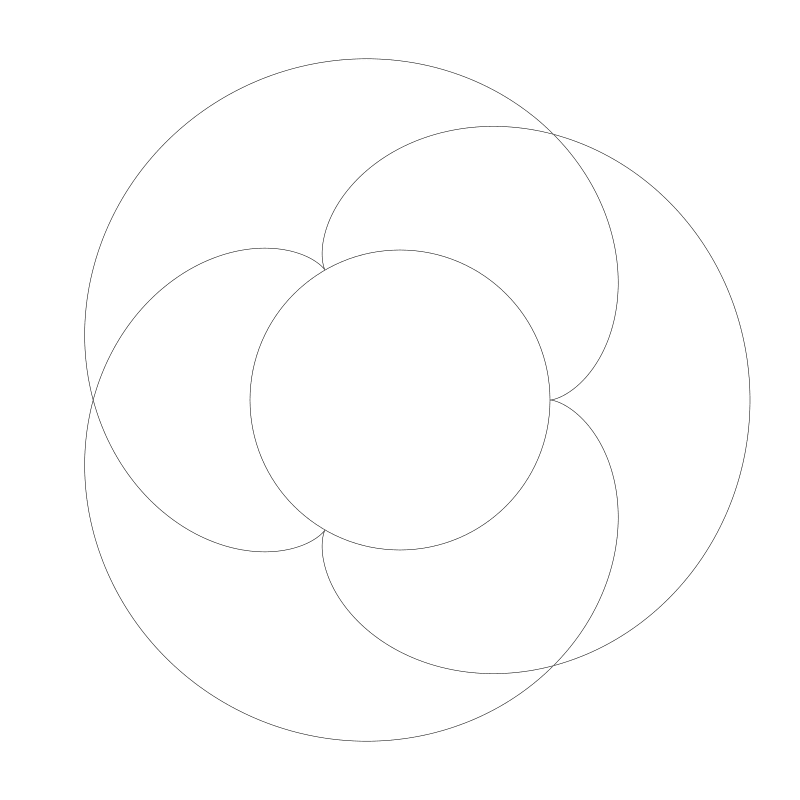
如果比例的第二個數位不是1,會如何?讓我們將 r0 設定為 150,r1 為 100。現在,ratio 為 3:2。

毫無意外,我們得到了一個半的結點(nodes)。為了完成這個曲線,我們不得不再繞一圈,需要將 t 的範圍值變為 0 到 PI * 4。然後得到結果:
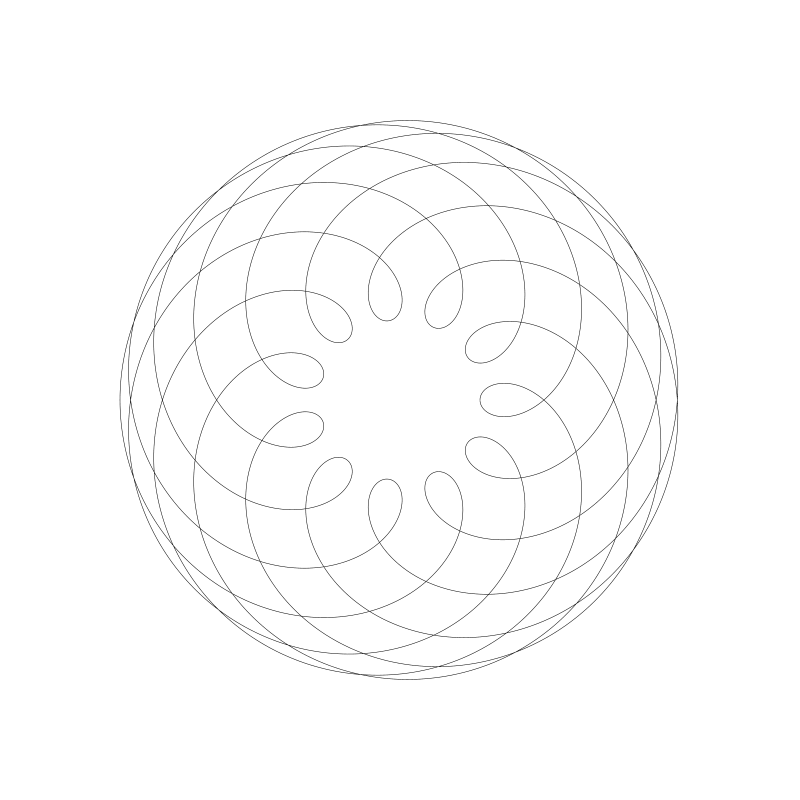
如果你使用整數,迴圈總是會完成的。在下一個例子中,比如是 11:7 ,所以不得不將 t 結束值調整為 PI * 14:

如果是 111:70, 意味著我需要 t 結束範圍調整至 140 * PI:
手動算這個有點痛苦,你可以建立個函數簡化比例計算並用分母 * PI * 2 作為迴圈次數。 下面有兩個有用的函數
//(譯者注: gcd 即 greatest common divisor 求最大公約數)
function gcd(x, y) {
result min(x, y)
while (result > 0) {
if (x % result == 0 && y % result == 0) {
break
}
result--
}
return result
}
function simplify(x, y) {
g = gcd(x, y)
return x / g, y / g
}
僅需要將 r0 和 r1 傳入 simplify 函數,得到簡化後的比例。將結果的第二個數位 * 2 * PI 做為迴圈的結束條件。下面是例子...
(譯得注:簡化比例式,最後將分母 * 2 * PI)
width = 800
height = 800
canvas(width, height)
translate(width/2, height/2)
r0 = 111
r1 = 70
d = 70
res = 0.01
num, den = simplify(r0, r1)
circle(0, 0, r0)
stroke()
for (t = 0.0; t < PI * 2 * den; t += res) {
x = (r0 + r1) * cos(t) - d * cos(((r0 + r1) * t) / r1)
y = (r0 + r1) * sin(t) - d * sin(((r0 + r1) * t) / r1)
lineTo(x, y)
}
stroke()
用化簡後的分數的分母保證迴圈足夠多閃以形成完整的曲線。
到目前為止,全部是外擺線(圓外旋輪線)。 讓我們改變引數 d 來建立一些其它的長短幅外擺線。
讓 d 大於 r1:
d 小於 r1:

在這些例子中我沒有再把內圓畫出來。
你無需讓我再提供更多的例子了。只需要改變數位看看能得到啥結果。
特殊長短幅外擺線
蚶線是長短幅擺線的一種,生成它的兩個圓半徑相等。如果兩個點在圓內,則它是特殊的蚶線被稱為 Cardioid 心形曲線。
下面是一個蚶線,兩個半徑都是 80 , d 值設為 160。
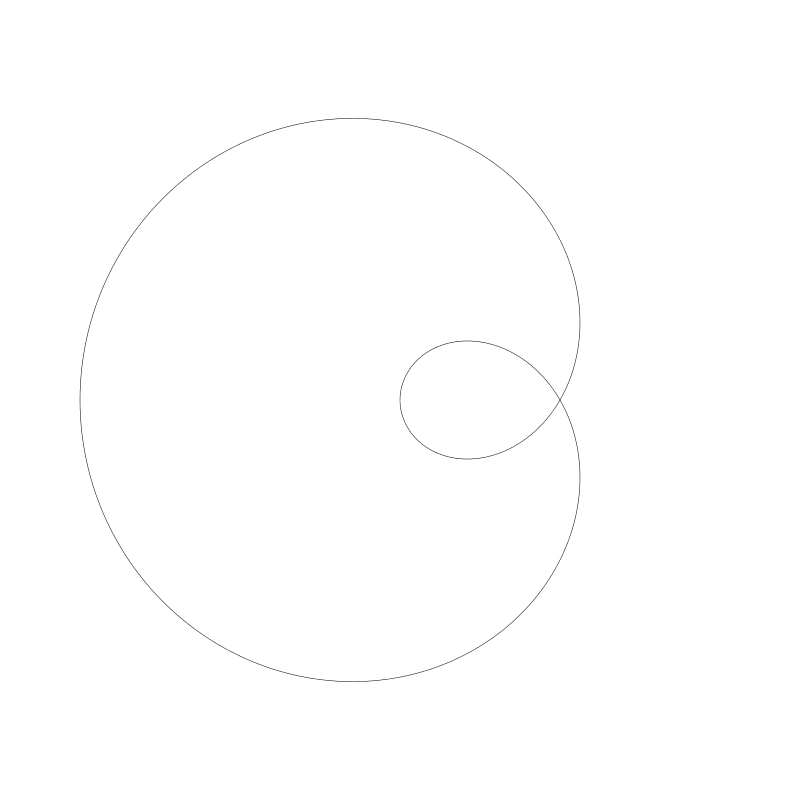
心形線三個值都設為 80

腎臟線是長短幅外擺線的一類,它的定圓半徑是動圓半徑的2倍,且那個點在動圓的圓周上。這是腎臟線的圖
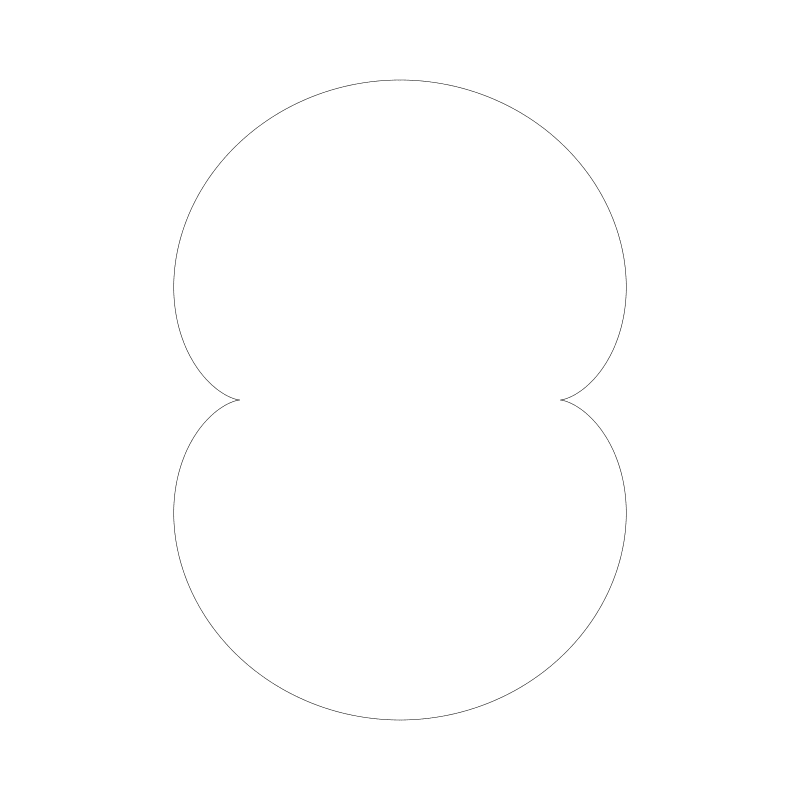
你也可以讓那個動圓上的點不在動圓圓周上,但卻不再是腎臟線了,但依然是很不錯的曲線。
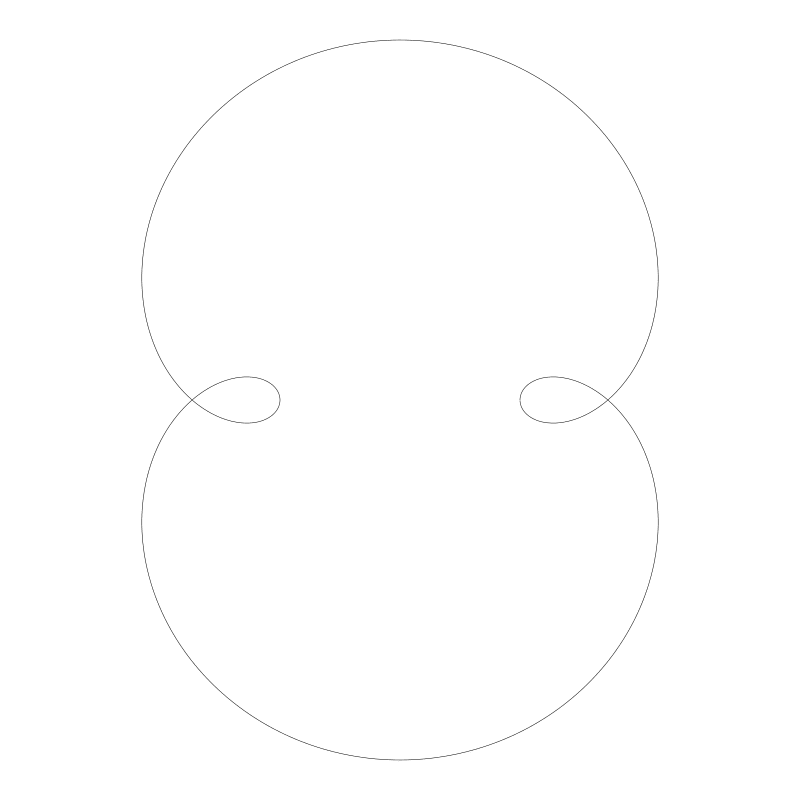
現在讓我們把視線轉向長短幅內擺線!
長短幅內擺線
正如前面提到的,長短幅內擺線其實就是動圓是延定圓內部捲動的。
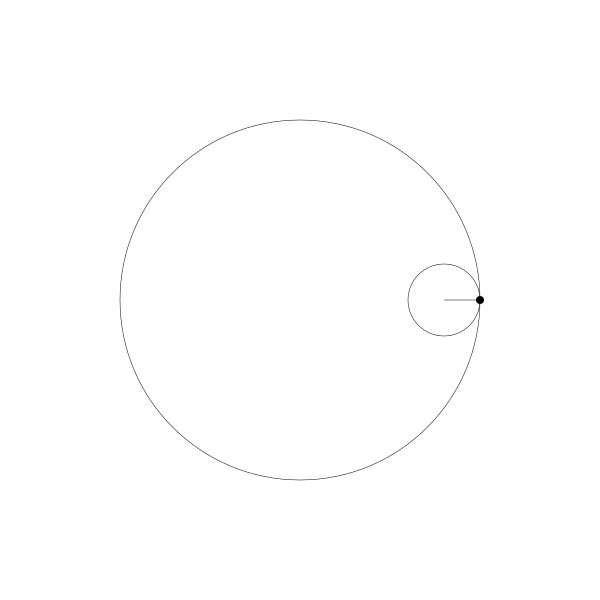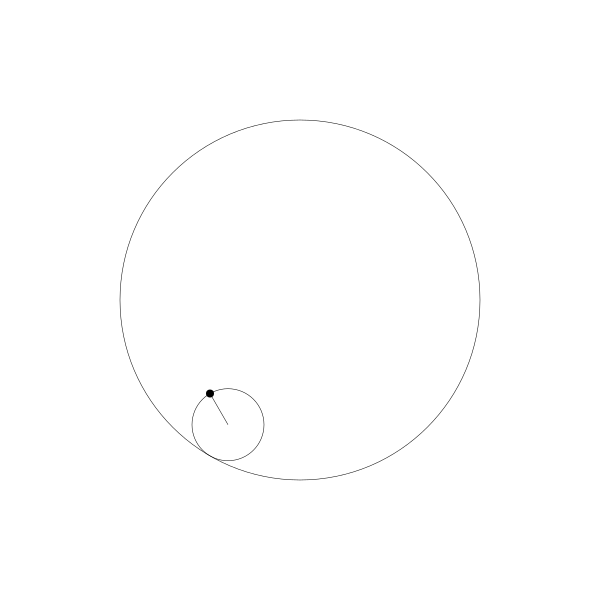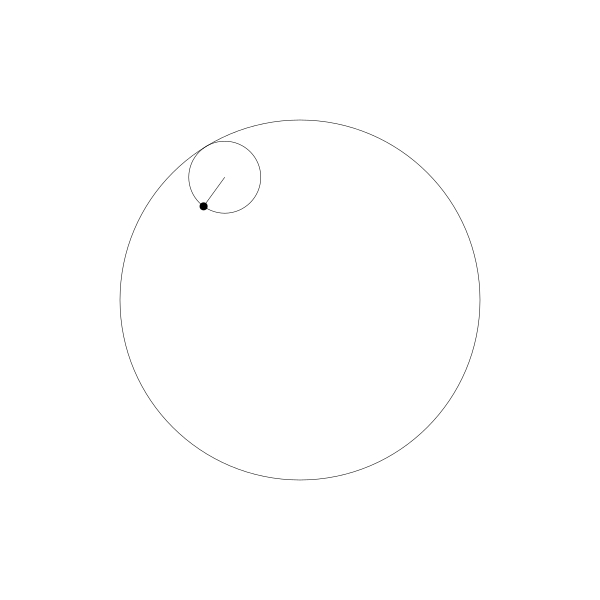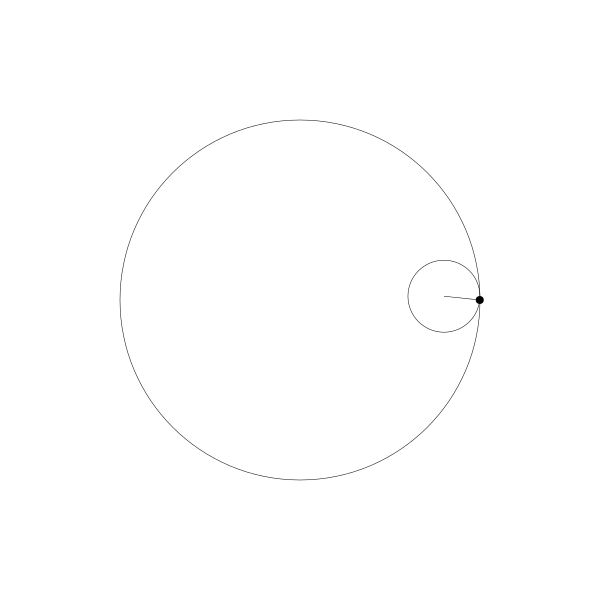
我們跟蹤那個曲線上的繪製點,就得到了長短幅內擺線
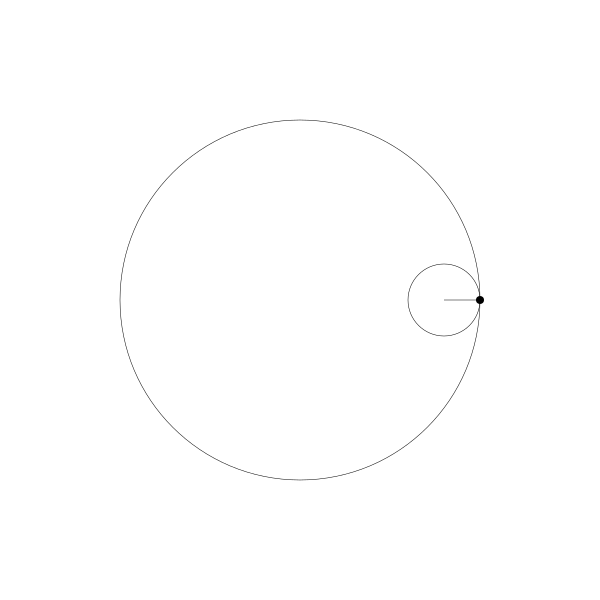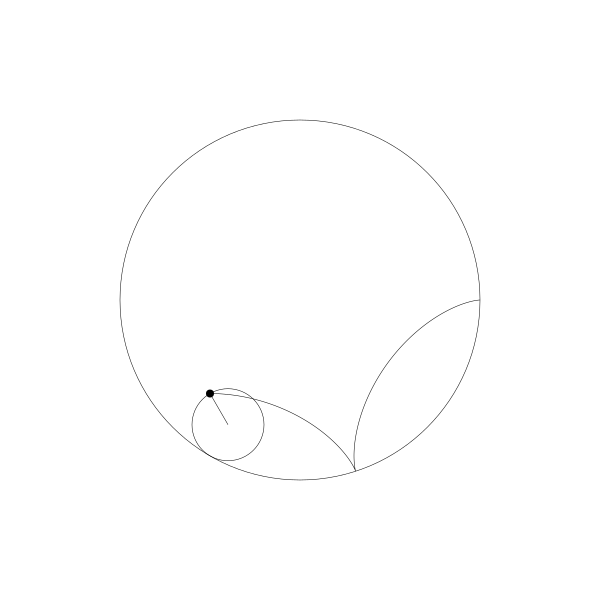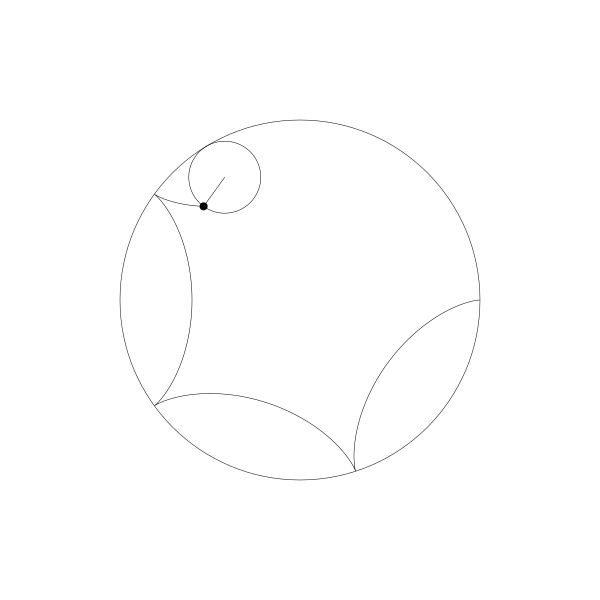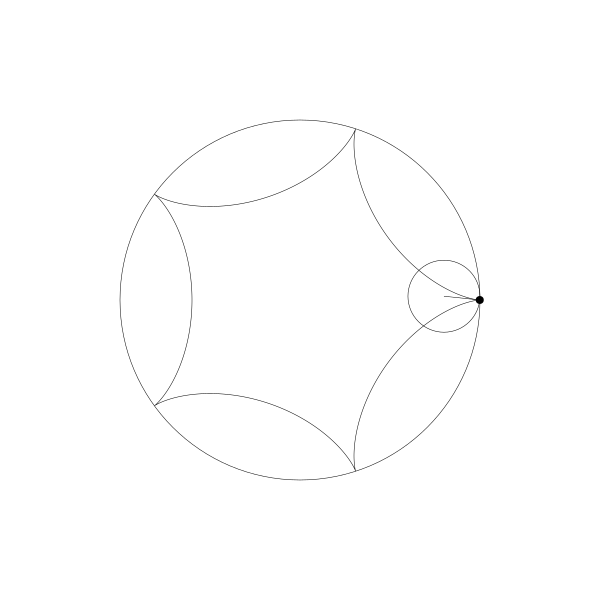
事實上,由於繪製點在動圓圓周上,它就是內擺線。
當繪製點移動到動圓外部, 得到的就是:
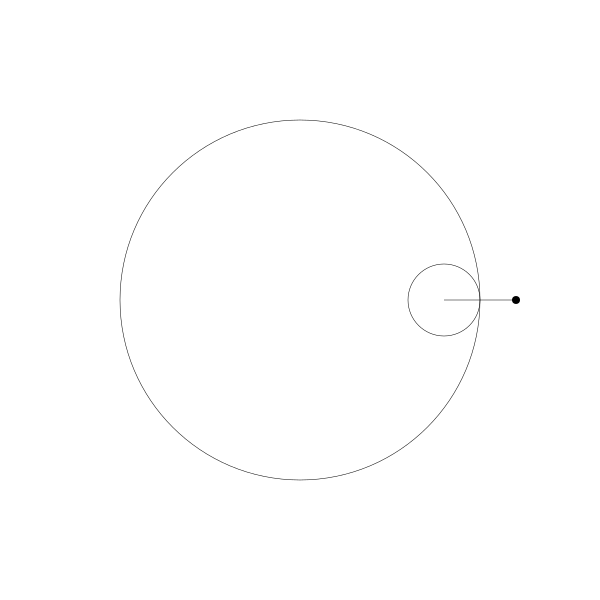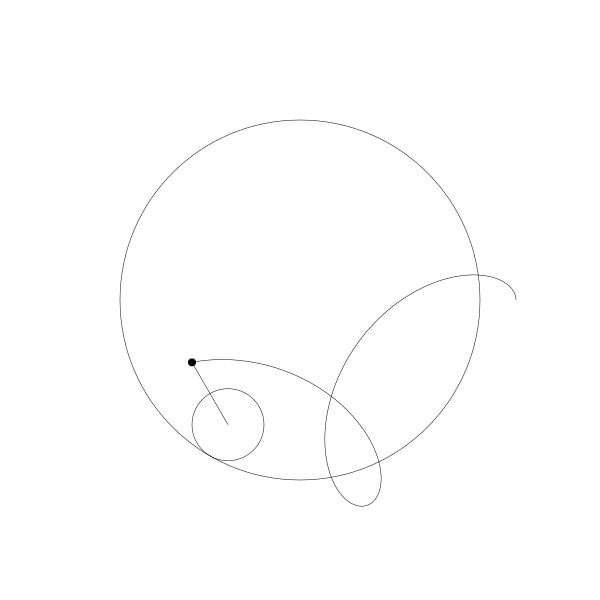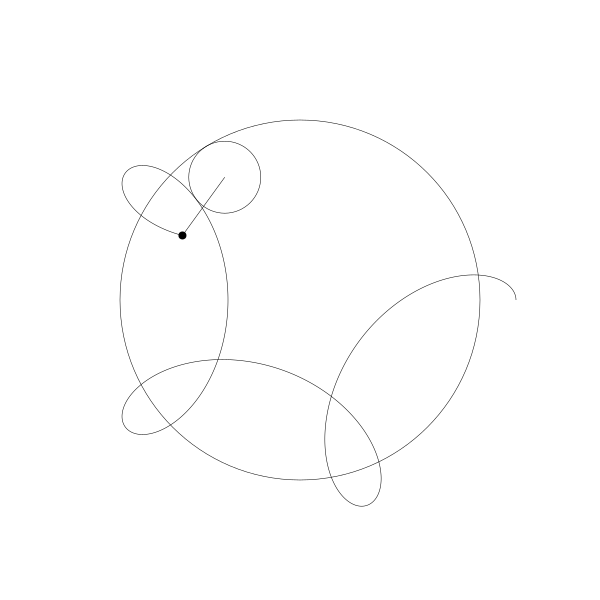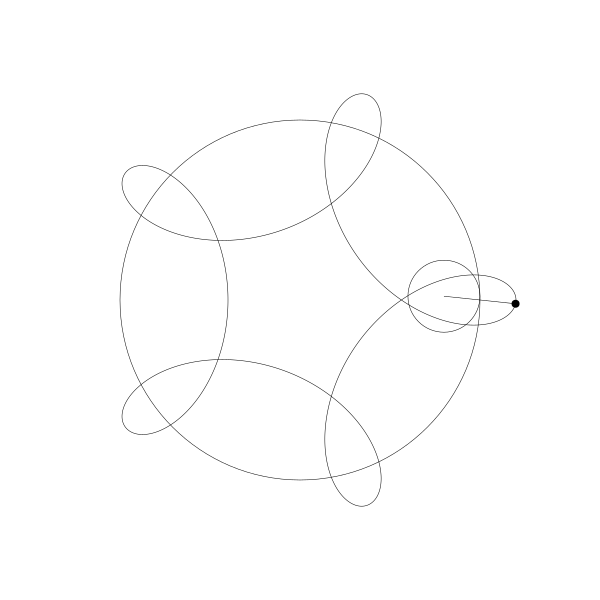
當繪製點移到動圓內部...
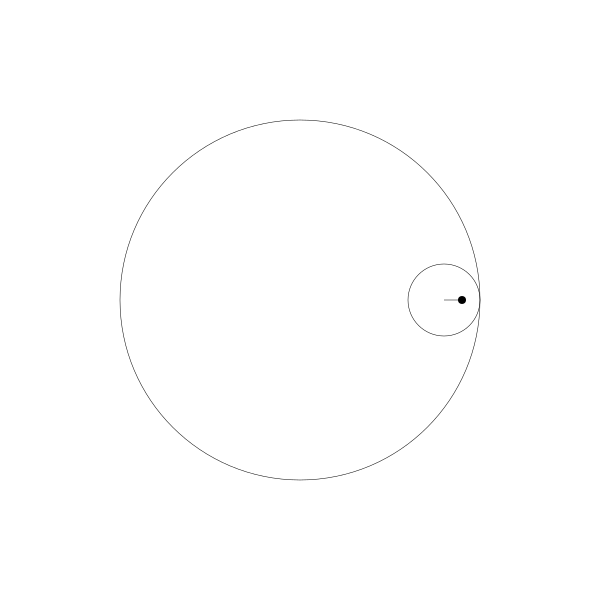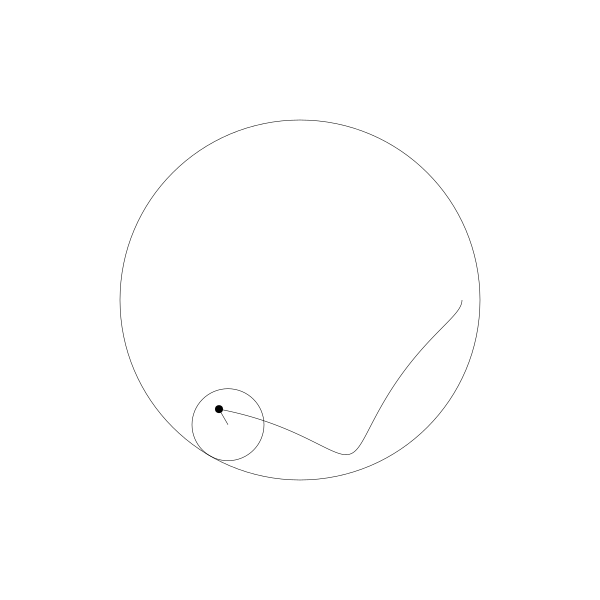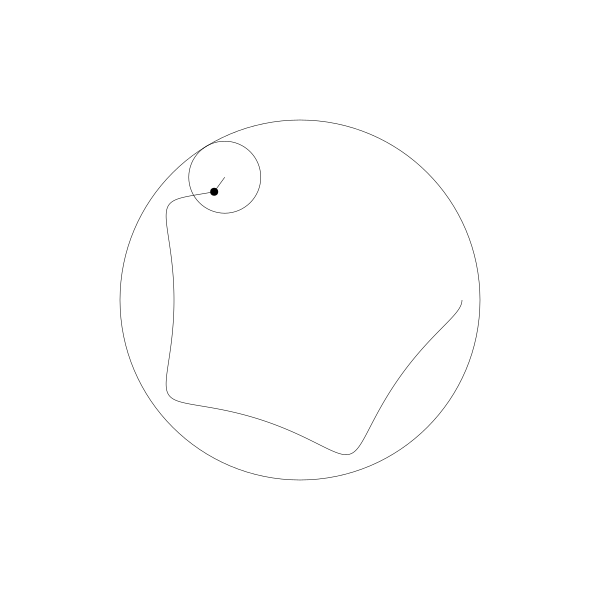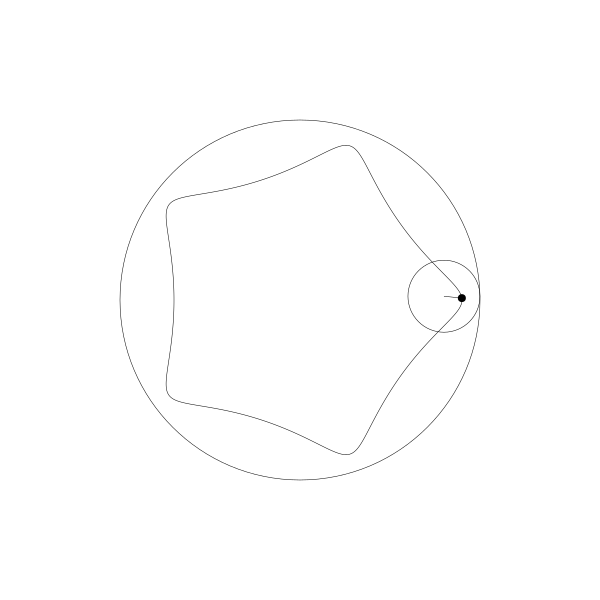
像之前一樣,這個動畫是用野路子建立的,其實是有簡單公式可以實現。
長短幅內擺線公式:
x = (r0 - r1) * cos(t) + d * cos(((r0 - r1) * t) / r1)
y = (r0 - r1) * sin(t) - d * sin(((r0 - r1) * t) / r1)
引數與長短幅外擺線類似,事實上公式也基本相同,僅有幾項符號不同。
下面是使用方法。
width = 800
height = 800
canvas(width, height)
translate(width/2, height/2)
r0 = 300
r1 = 50
d = 50
res = 0.01
num, den = simplify(r0, r1)
for (t = 0.0; t < PI * 2 * den; t += res) {
x = (r0 - r1) * cos(t) + d * cos(((r0 - r1) * t) / r1)
y = (r0 - r1) * sin(t) - d * sin(((r0 - r1) * t) / r1)
}
stroke()
程式碼執行結果:
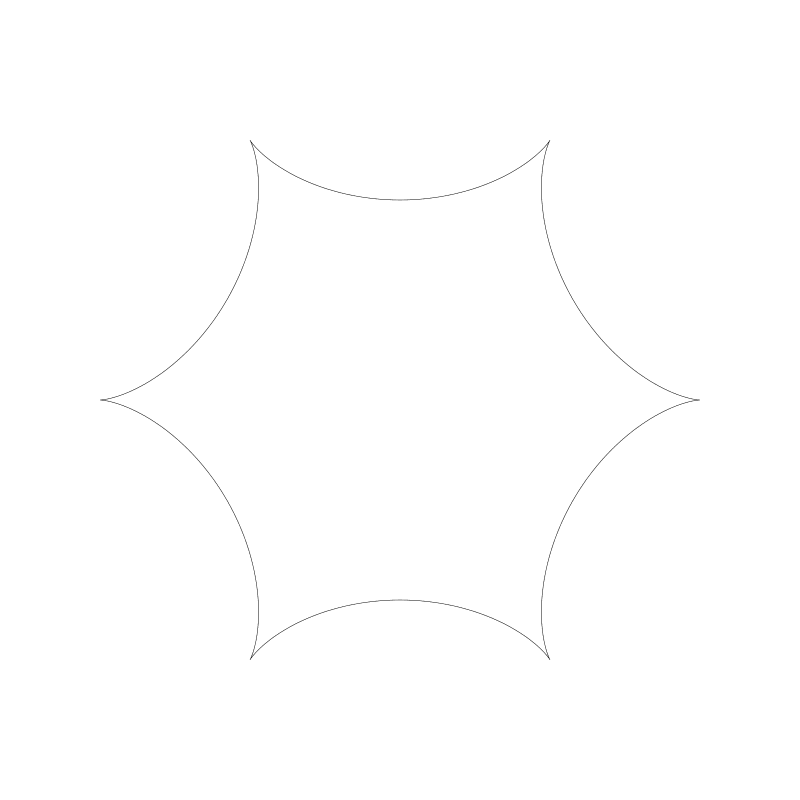
注意 r0 與 r1 比例是 6:1, 擁有 6 個點。比例的作用原理與之前的長短幅外擺線一樣
下面是半徑 312 和 76 (譯者注:這裡 r0 為 312,r1,d 都為 76):
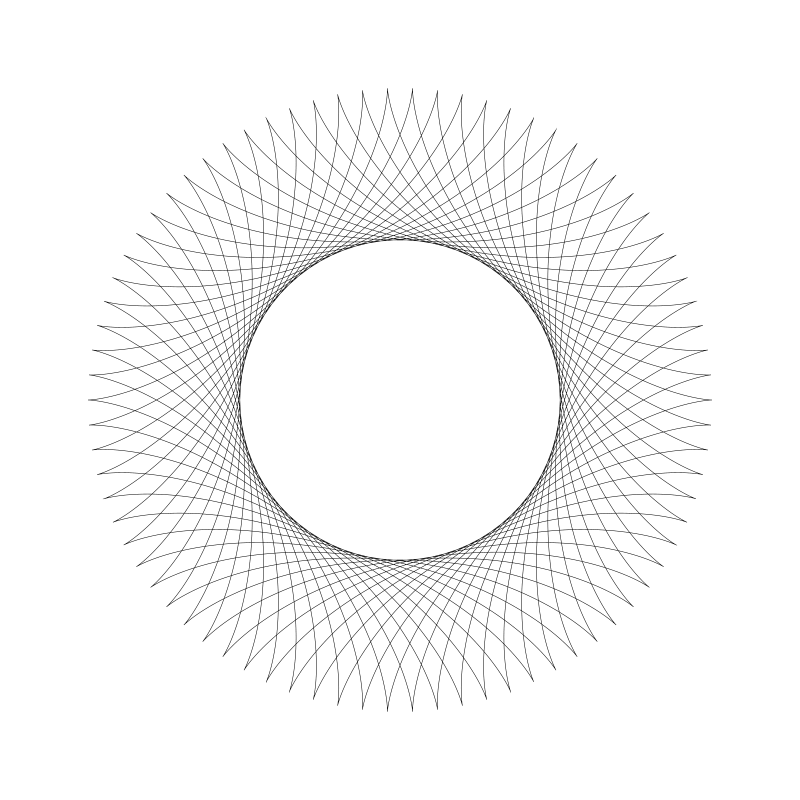
將繪製點 d 值設大一點移出動圓圓周:
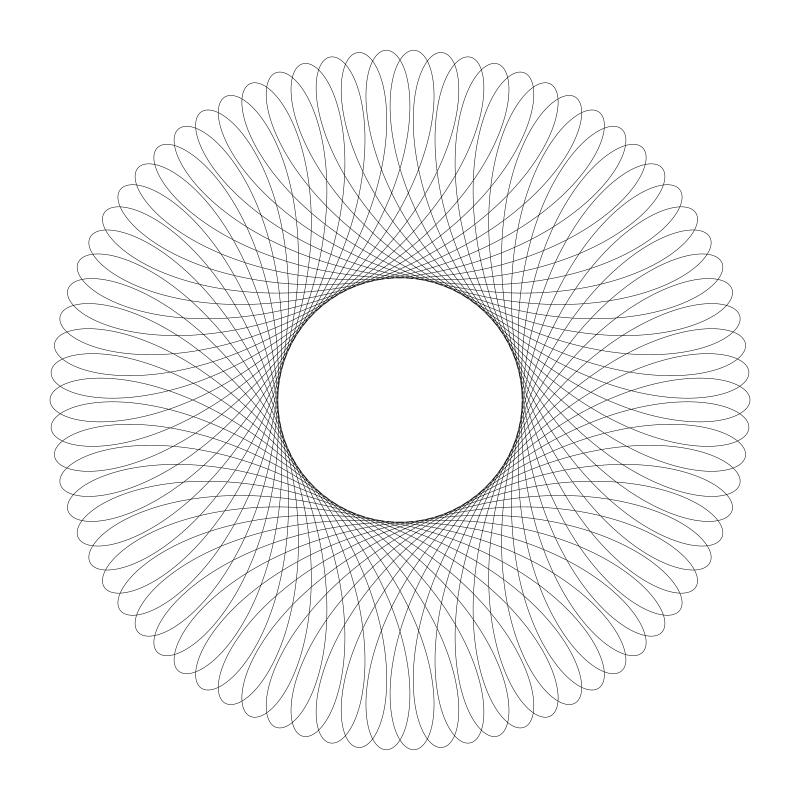
移入動圓內...
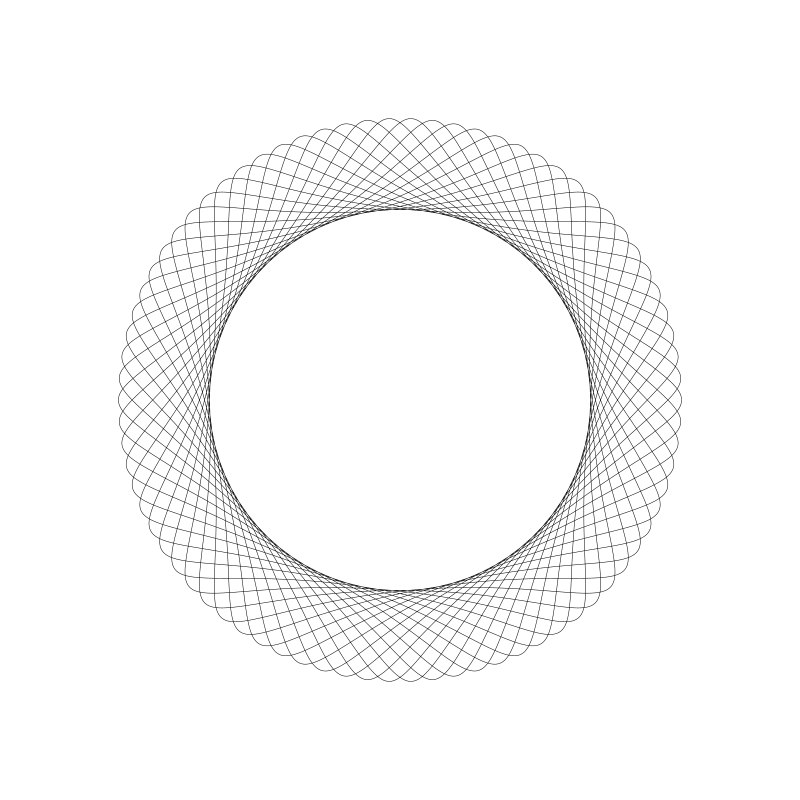
如果你不斷嘗試,我保證你能發掘出更多有趣的圖形。
特殊長短幅內擺線
我將再介紹兩種特殊長短幅內擺線。我們需要再次調整兩個圓的大小比例。
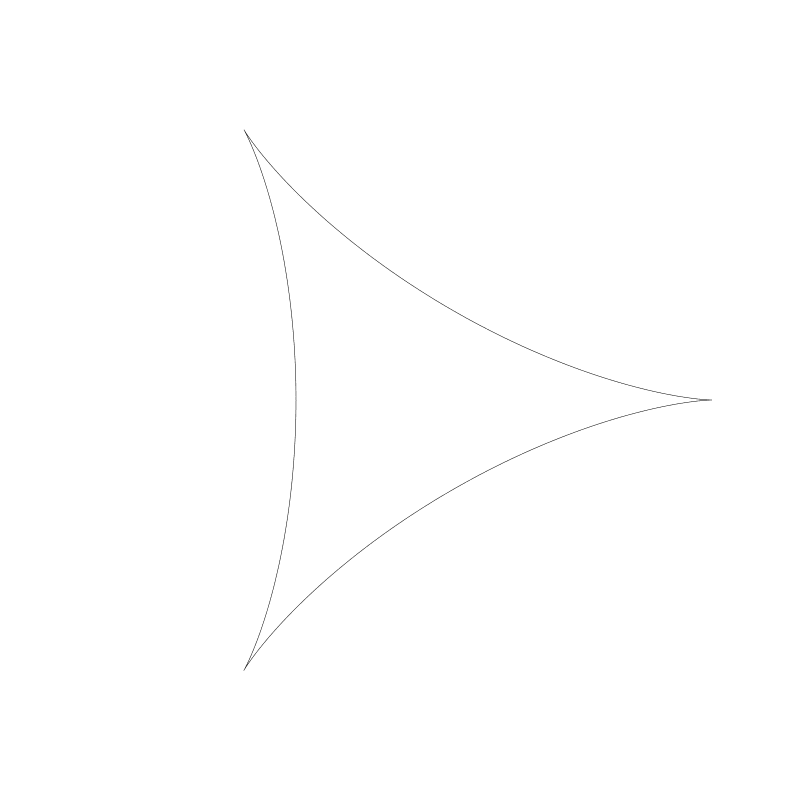
這是星狀圖的比例 4:1
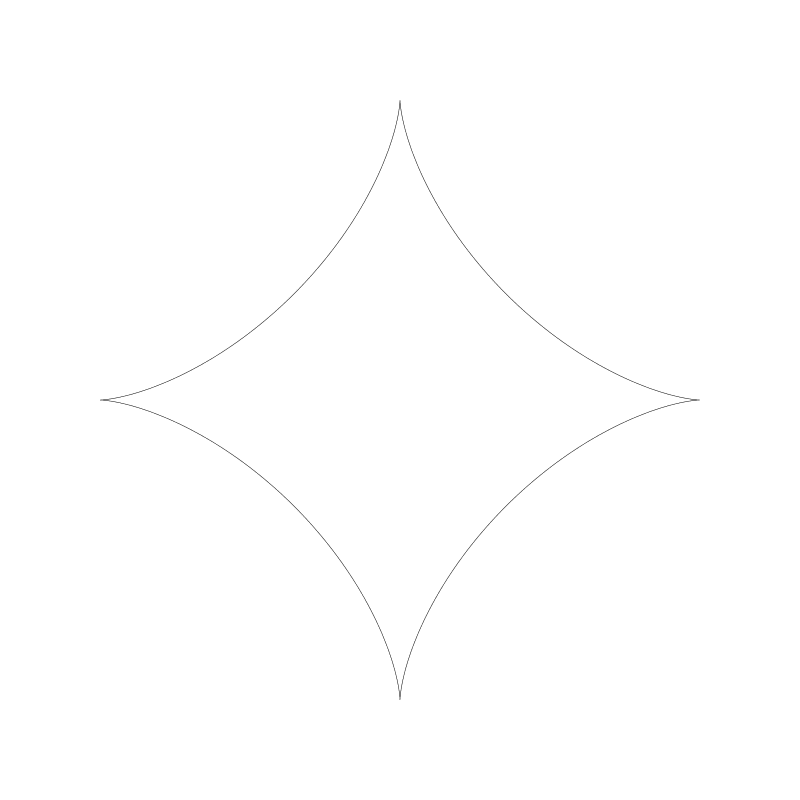
還有一個更有趣的比例 2:1. 被稱為圖斯雙圓,以描述它的13世紀波斯天文學家名字而命名。下面是演示它的動畫。
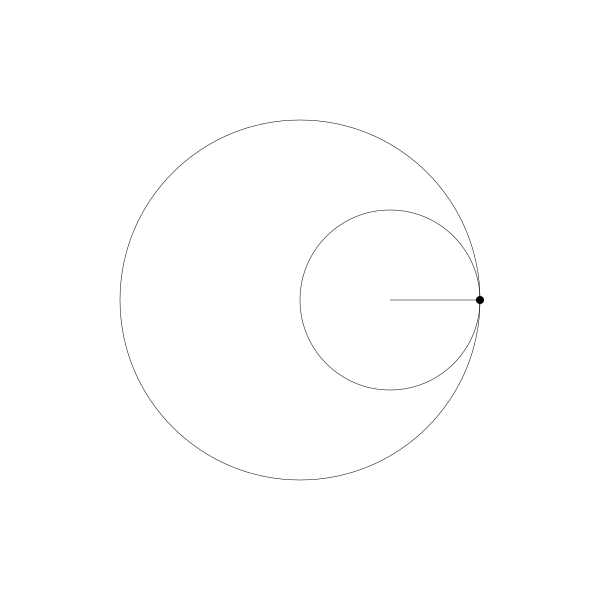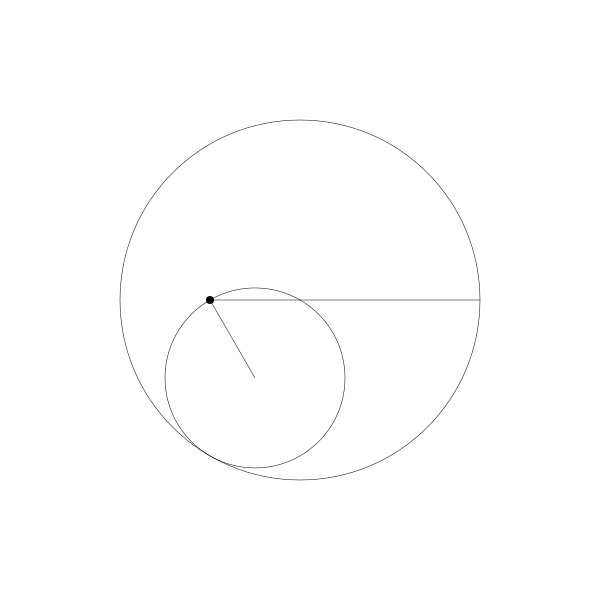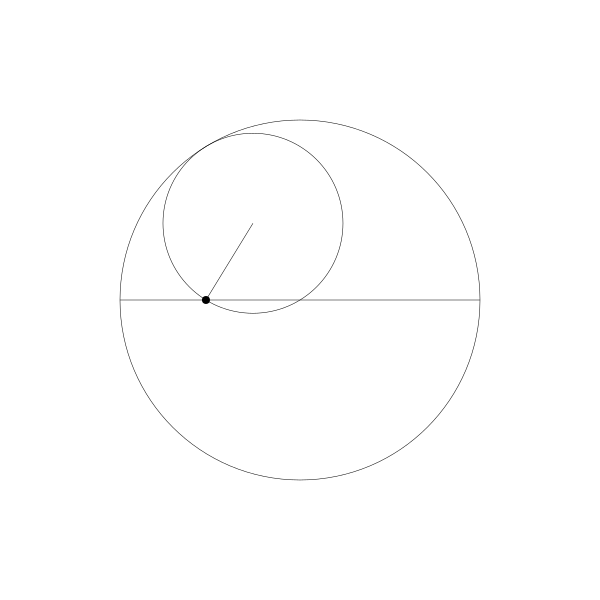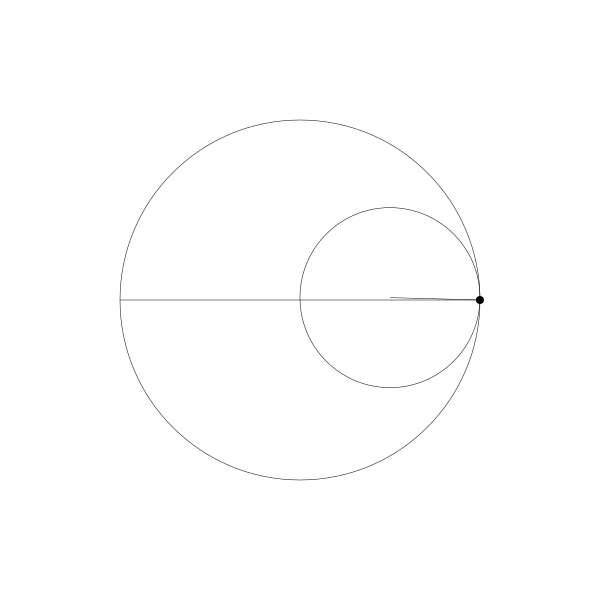
正如你所看到的,形成了一條直線。
如果你多建立幾個動圓,並將每個動圓的繪製點相位與前一個相比再往後調整一點,你將會得到如下圖:
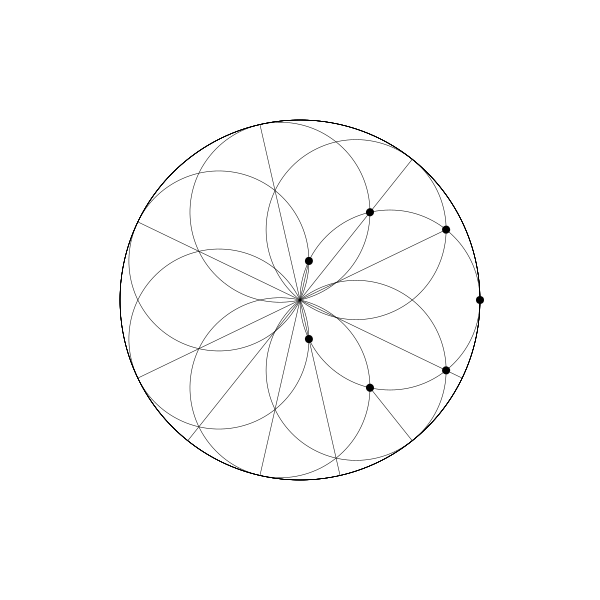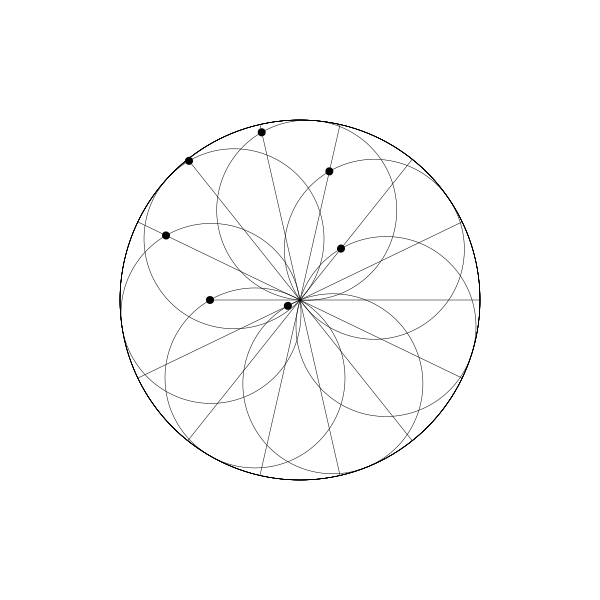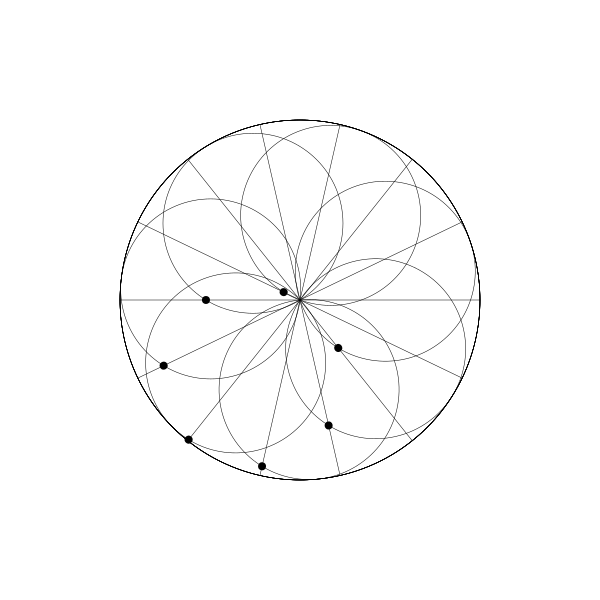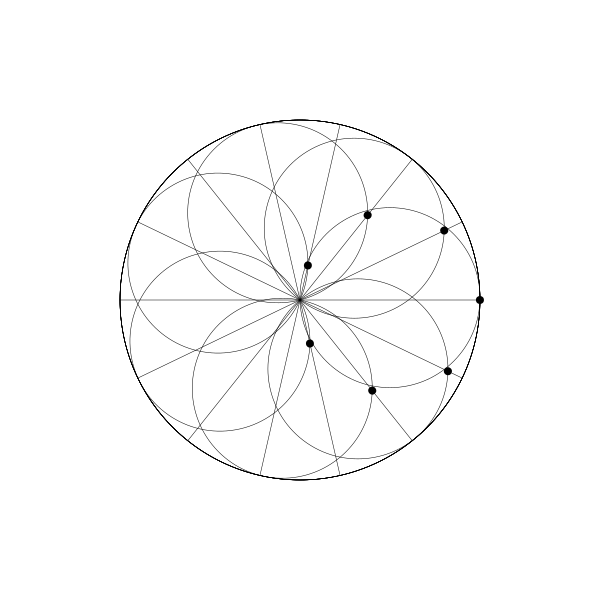
每個點延直線來回運動。如果你將所有線條和動圓移除,你會得到一個旋轉的圓的錯覺。事實上,它看起來像是另一個內擺線
螺旋圖!
小時候如果你像我一樣比較呆,那麼你可能也會像我這樣擁有下面這些東西(譯者注:可能我不夠呆,反正我沒有過,倒是見過同學有類似的東西--!):

這是幾個星期前為寫這一章內容我新買的。它很酷,錫盒子包裝內包含了一些繪製用的紙還有使用說明和靈感小冊子。

大的齒輪固定在紙上。過去用的是小釘子,現在用的是用粘粘的東西(sticky-tack 多偉大的改進!)固定住,還有一些小的多孔的小齒輪。你將筆插進這些小孔中,讓它延著大圓旋轉一圈。

瞧!一個長短幅內擺線

如果你將小齒輪擺外面滾一輪,它就是長短幅外擺線。相當有趣,說實施,我還是更喜歡用程式碼實現它。下面是繪製過程中筆滑了,這讓線條看起來有點兒亂。筆觸也斷斷續續的。

當我玩的過程中才發現,它只能畫出短幅擺線和內擺線。繪製點只能是在移動的齒輪內。
本章 Javascript 原始碼 https://github.com/willian12345/coding-curves/blob/main/examples/ch09
部落格園: http://cnblogs.com/willian/
github: https://github.com/willian12345/