貝賽爾曲線（Bézier Curves）

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

譯者：池中物王二狗(sheldon)

blog: http://cnblogs.com/willian/

原始碼：github: https://github.com/willian12345/coding-curves

曲線藝術程式設計系列第8章 貝賽爾曲線

讓我們回到真正的曲線上來。貝賽爾曲線程式設計就非常有趣領人止不住的想探索一翻， 你可以自己深入學習它的組成以及相應的公式。在我的視訊或我的書裡面這些事我做過很多次了。 下面是我做的兩個視訊你可以先看看：

https://www.youtube.com/watch?v=dXECQRlmIaE
https://www.youtube.com/watch?v=2hL1LGMVnVM

這是 Freya Holmer的 （譯者注：此女的視訊相當給力）

https://www.youtube.com/watch?v=aVwxzDHniEw
https://www.youtube.com/watch?v=jvPPXbo87ds

我還是僅限介紹最基礎的一些函數以及這些年積累的一些很酷實用技巧與經驗。

基礎

貝塞爾曲線由兩個端點和一個控制點定義而成。它從一個點出發向控制點（不穿過控制點）再至另一個端點。你可以通過控制這些點中的任意改變曲線的形狀。這些曲線通常很優美，應用於各種各樣的設計工具，從繪製文字到繪製汽車，它是各種形狀繪製的關鍵組成部分。

二階貝塞爾曲線

兩個端點與一個控制點組成，如下：

控制點靠近 canvas 底部。如果你把它移動到右邊，它會影響到曲線：

細一點的線和那個點主要用於視覺化演示控制點的位置。

三階貝塞爾曲線

三階貝塞爾曲線擁有兩個端點和兩個控制點，如圖：

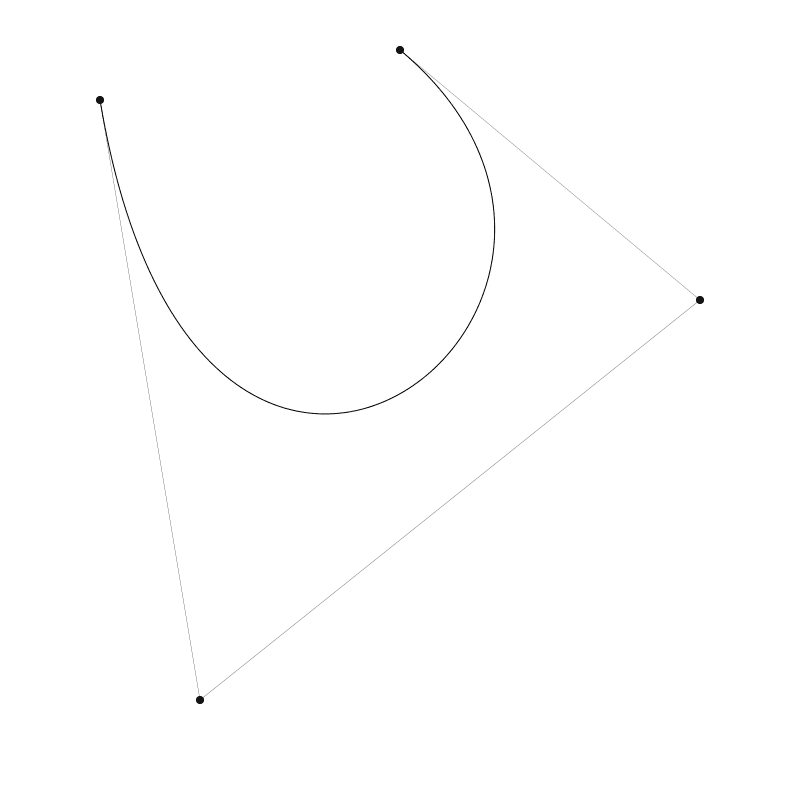
高階貝塞爾曲線擁有更多的控制點，但花費的計算成本也相應會變的更高。 可以看看 Freya 的相關視訊講解。

大多數繪圖程式 api 都有提供二階和三階曲線的函數，但名字可能有比較大的出入。

我看過二階貝塞爾曲線的函數有被命名為：

• curveTo
• quadraticCurveTo

三階貝塞爾曲線被命名為:

• curveTo
• cubicCurveTo
• bezierCurveTo

你得確保你使用的程式語言用的是哪一個。通常你可以參考上面列出的幾個例子，起始點用 moveTo 定義， 否則起點將會是繪圖 api 最近一次的繪製點，然後呼叫貝塞爾曲線函數定義控制點與結束點。你可以像下面這麼做：

moveTo(100, 100)
cubicCurveTo(200, 100, 200, 500, 100, 300)
stroke()

但有些程式語言可以允許你一次設定所有點。它是作為基礎的內建函數，當然我們還是會忽略具體內建的 api 我們必須自己實現一遍。

貝塞爾曲線編碼

我們先從二階貝塞爾曲線開始然後轉向三階貝塞爾曲線。但在我們開始畫曲線路徑前，我們需要先另外建立一個基礎函數。它會提供貝塞爾曲線上任意點的點的位置。

二階貝塞爾曲線

有趣的一點是貝塞爾曲線基礎公式是一維的。為達到二維，三四，或更高階，你權需為每一維應用公式。這裡我們需要用兩個一維組合成二維，所以我們將執行兩次。單引數公式如下：

x = (1 - t) * (1 - t) * x0 + 2 * (1 - t) * t * x1 + t * t * x2

此處，x0, x1, 和 x2 是兩個端點與控制點，t 的值範圍是 0.0 到 1.0。 它會根據 t 的值返回這條貝塞爾曲線上對應 x 點。 當 t 為 0， x 等於 x0。 當 t 為 1， x 等於 x2。 當 t 在 0 和 1 之間時，x 會是是插值。

所以要建立一個二階貝塞爾曲線點的函數應該像下面這樣做：

function quadBezierPoint(x0, y0, x1, y1, x2, y2) {
  x = (1 - t) * (1 - t) * x0 + 2 * (1 - t) * t * x1 + t * t * x2
  y = (1 - t) * (1 - t) * y0 + 2 * (1 - t) * t * y1 + t * t * y2
  return x, y
}

你可以這麼做，如果你的程式語言支援返回多個值的話。否則你需要將返回值變成類似點物件。

注意，我們先去重一下。我們可以先提取 1-t 為 m 因子：

function quadBezierPoint(x0, y0, x1, y1, x2, y2, t) {
  m = (1 - t)
  x = m * m * x0 + 2 * m * t * x1 + t * t * x2
  y = m * m * y0 + 2 * m * t * y1 + t * t * y2
  return x, y
}

然後

function quadBezierPoint(x0, y0, x1, y1, x2, y2, t) {
  m = (1 - t)
  a = m * m
  b = 2 * m * t
  c = t * t
  x = a * x0 + b * x1 + c * x2
  y = a * y0 + b * y1 + c * y2
  return x, y
}

無它，就是更易讀。

有了它就可以用它畫二階貝塞爾曲線了。為了清晰的定義二階與三階，我把它們分別命名為 quadCurve 和 cubicCurve。

function quadCurve(x0, y0, x1, y1, x2, y2, res) {
  moveTo(x0, y0)
  for (t = res; t < 1; t += res) {
    x, y = quadBezierPoint(x0, y0, x1, y1, x2, y2, t)
    lineTo(x, y)
  }
  lineTo(x2, y2)
}

確保在 quadCurve 我們將起始點與結束點拆出來了，我們 moveTo 拆出第一個點，用 lineTo 拆出最後一個點。 函數接受一個 res 引數，用於指定沿曲線上迭代多少次。我們將 t 初始值為 res 因為函數外已經移動到第一個點了，無論 t 值是否為 0。中間的所有點根據當前 t 繪製出線條。

當然，你也可以建立一個 quadCurveTo 函數去掉函數內前兩個引數還有 moveTo（譯者注：這裡並非是讓你去掉，而是讓你自己決定是否單獨在函數外面呼叫）。 這取決於使用者自己是否需要指定曲線起始點（或從已有的路徑開始繪製）。以下是呼叫方式：

canvas(800, 800)
quadCurve(100, 100, 200, 700, 700, 300, 0.01)
stroke()

這會生成如下圖：

如果 res 變大一點，則會生成一個有點糙的曲線：

你已經對 res 解析度這個值有一定經驗了。內建的貝塞爾曲線會自動給定一個合適的 res 值。但我們自己實現的 quadCurve 函數內 res 值可能還是有點兒問題的。但在此處並不重要，因為它已經能讓 quadBezierPoint 返回給我們足夠的座標值了，正如你所見的這樣。

我們的 quadBezierPoint 能用於實現動畫，而內建函數做不到（譯者注：內建函數只能一次性畫出路徑）。在這一節， 就像之前章節我做的那樣， 我已經假定你有或有能力實現無限迴圈的函數用於建立動畫了。 還是叫它 loop 函數。 我不會像之前那樣用 t 實現 0 到 1 繪製曲線，我將 讓 t 從 0 到 finalT , finalT 的值會一直變化。

canvas(400, 400)
x0 = 50
y0 = 50
x1 = 150
y1 = 360
x2 = 360
y2 = 150
finalT = 0
dt = 0.01
res = 0.025
 
function loop() {
  clearCanvas()
  moveTo(x0, y0)
  for (t = res; t < finalT; t += res) {
    x, y = quadBezierPoint(x0, y0, x1, y1, x2, y2, t)
    lineto(x, y)
  }
  stroke()
 
  // add to finalT
  finalT += dt
 
  // if we go past 1, turn it around
  if (finalT > 1) {
    finalT = 1
    dt = -dt
  } else if (finalT < 0) {
    // if we go past 0, turn it back
    finalT = 0
    dt = -dt
  }
}

結果應該會像下面這樣的動畫

此處， for 環境內 t 是從 res 到 finalT 變化的所以不會畫出完整的曲線（除非 finalT 為 1）。然後我們給 finalT 加上 dt。 這會讓 finalT 慢慢接近 1， 這會曲線越來越完整。當 finalT 超過 1 時, 我們將它設為負值，這會讓整個過程反轉直到 finalT 變為 0， 這是我們變回出發點的方法。（譯都注：其實就是當 finalT 超過臨界點後，通過將 dt 設為 -dt 使得 finalT 一直在 1 和 0 之間來回變動）

相比於畫一條線， 我們這次做一個沿貝塞爾曲線運動的動畫！下面是程式碼範例。相當清晰明瞭。我只是新增了一個實心圓的邏輯放進 loop 函數內，剩下的程式碼和之前一樣。

function loop() {
  clearCanvas()
 
  x, y = quadBezierPoint(x0, y0, x1, y1, x2, y2, finalT)
  circle(x, y, 10)
  fill()
 
  // no changes beyond here...
  // add to finalT
  finalT += dt
 
  // if we go past 1, turn it around
  if (finalT > 1) {
    finalT = 1
    dt = -dt
  } else if (finalT < 0) {
    // if we go past 0, turn it back
    finalT = 0
    dt = -dt
  }
}

這樣我們就得到了 finalT 的當前值對應點的 x, y 並在 x, y 處畫了個圓。假定你已經有了 circle 繪製函數。你如果有需要你可以在第三章裡複製一個過來。

在下面這個 gif 圖，是我用內建的函數繪製的相同曲線，多來了一條細線表示運動軌道展示動畫一直在我們我們定義的標準的二階貝塞爾曲線上。

好的，稍作休息後讓我們進入三階貝塞爾曲線。

三階貝塞爾曲線

上面介紹的二階貝塞爾曲線都將應用到三階上。只是公式不一樣 - 更復雜一點點。下面是一維的定義：

x = (1 - t) * (1 - t) * (1 - t) * x0 + 3 * (1 - t) * (1 - t) * t * x1 + 3 * (1 - t) * t * t * x2 + t * t * t * x3

還有二維函數的定義：

function cubicBezierPoint(x0, y0, x1, y1, x2, y2, x3, y3, t) {
  x = (1 - t) * (1 - t) * (1 - t) * x0 + 3 * (1 - t) * (1 - t) * t * x1 + 3 * (1 - t) * t * t * x2 + t * t * t * x3
  y = (1 - t) * (1 - t) * (1 - t) * y0 + 3 * (1 - t) * (1 - t) * t * y1 + 3 * (1 - t) * t * t * y2 + t * t * t * y3
  return x, y
}

是的看起來相當亂，我們同樣提取出 1- t 因子出來整理一下：

function cubicBezierPoint(x0, y0, x1, y1, x2, y2, x3, y3, t) {
  m = 1 - t
  x = m * m * m * x0 + 3 * m * m * t * x1 + 3 * m * t * t * x2 + t * t * t * x3
  y = m * m * m * y0 + 3 * m * m * t * y1 + 3 * m * t * t * y2 + t * t * t * y3
  return x, y
}

好一點兒了，更進一步優化後：

function cubicBezierPoint(x0, y0, x1, y1, x2, y2, x3, y3, t) {
  m = 1 - t
  a = m * m * m
  b = 3 * m * m * t
  c = 3 * m * t * t
  d = t * t * t
  x = a * x0 + b * x1 + c * x2 + d * x3
  y = a * y0 + b * y1 + c * y2 + d * y3
  return x, y
}

還可以！

現在可以建立 cubicCurve 三階貝塞爾曲線函數了。

function cubicCurve(x0, y0, x1, y1, x2, y2, x3, y3, res) {
  moveTo(x0, y0)
  for (t = res; t < 1; t += res) {
    x, y = cubicBezierPoint(x0, y0, x1, y1, x2, y2, x3, y3, t)
    lineTo(x, y)
  }
  lineTo(x2, y2)
}

很簡單。我想不需要更多的解釋了。

現在你的任務是：調整二階動畫用三階來實現一遍。僅僅需要加一個　x3, y3 的新座標點並呼叫這個新函數。

這些就是對貝塞爾曲線和路徑的基礎程式碼實現了。但我這裡還準備了一些其它有用的小技巧給你。

過點畫線

那些剛開始使用貝塞爾曲來執行緒式設計的人經常會說

這很巧妙，但我希望曲線能穿過控制點 ---- 這也是我-大約在 2000 年左右想要實現的功能

當然可以實現了！這對二階貝塞爾曲線相當容易實現。你只需要在更遠的地方建立另一個控制點，控制曲線剛好穿過原控制點的位置。新的控制點很容易計算。以點 x0, y0, x1, y1, x2, y1 為例，那麼新控制點會是：

x = x1 * 2 - x0 / 2 - x2 / 2
y = y1 * 2 - x0 / 2 - x2 / 2

現在我們可以建立地一個新函數 quadCurveThrough 實現上面的程式碼公式。下面是計算獲取新控制點並使用內建函數實現貝塞爾曲線繪製。我假定你的系統中也有名為 quadraticCurveTo 的函數，當然也可能名字不同。

function quadCurveThrough(x0, y0, x1, y1, x2, y2) {
  xc = x1 * 2 - x0 / 2 - x2 / 2
  yc = y1 * 2 - y0 / 2 - y2 / 2
  moveTo(x0, y0)
  quadraticCurveTo(xc, yc, x2, y2)
}

下圖中紅的是我用標準的二階貝塞爾曲線畫的，藍的是用新函數畫的。並且繪製了那些控制點用於證明。

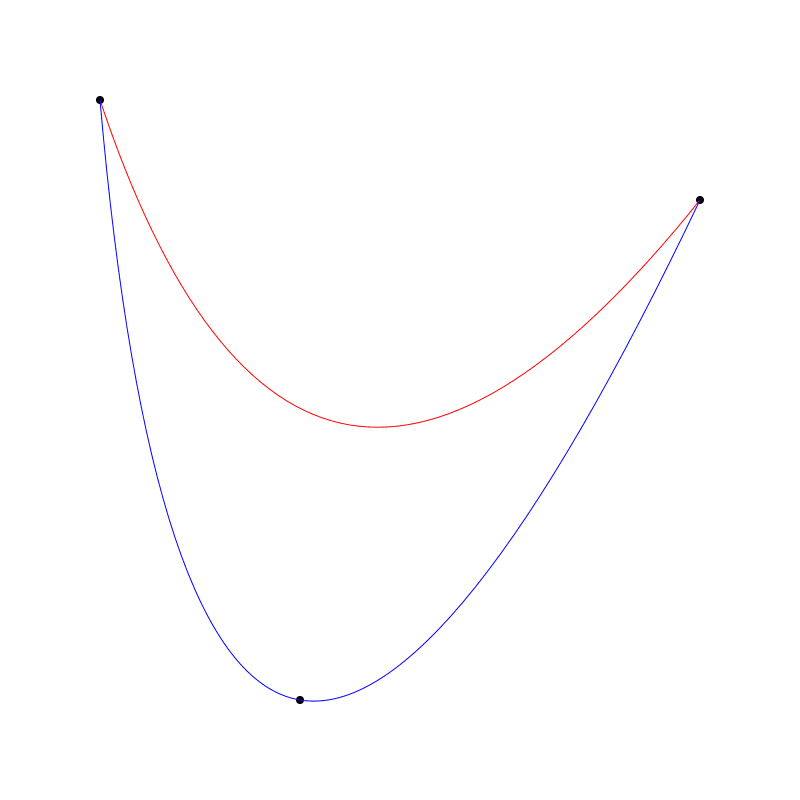
你下一個問題一定是如何在三階貝塞爾曲線實現同樣的過控制點繪製曲線。我暫時還不知道，但我會一直探索。我猜這也是一個機會，也許有人會在評論區給出答案，或直接告訴我這不可能實現