決策樹(實驗室會議小記)
特徵選擇
為什麼要進行特徵選擇?
特徵過多導致過擬合、有一些特徵是噪音。
特徵選擇技術:
1、 嘗試所有組合:也是全域性最優
2、貪婪演演算法:每次決策都是基於當前情況去尋找最優解。計算過程:把特徵加進去→是否更優?→是:加入模型/否:淘汰
3、L1正則:目標函數為損失函數;特點:具有稀疏性
4、決策樹:節點代表每個特徵選擇。優點:便於處理高維資料
5、相關性計算:一種脫離模型內部結構而直接分析特徵\(x_i\)和標籤y的相關性的方法。主要是計算向量相似度的方法。
總結:都是對比了各個特徵的優劣,如何計算優劣的方法不同。
L1正則化
次梯度下降
L1正則特徵選擇問題
彈性網路迴歸
1、計算上:
(1)相關性:計算\(x_i、y_i\),扔掉差的
(2)主成分:只計算\(x_i\)
問題:
(1) 為什麼資訊熵這麼計算?
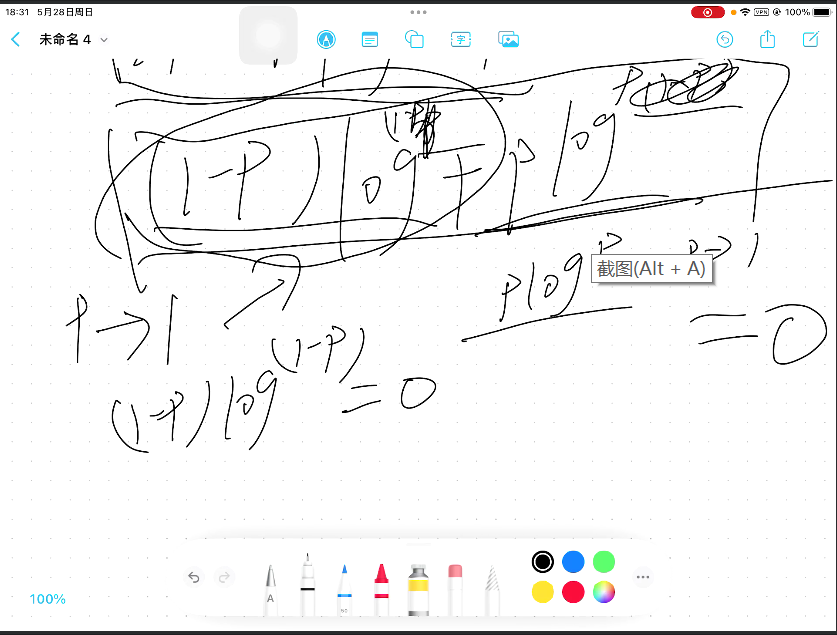
資訊熵在神經網路里面也叫交叉熵,所有二分類問題都是這麼算的。交叉熵在預測對的時候p為0/1,如果是0.5那麼是不對的。
(2) 貪婪演演算法為什麼降低了複雜度?
假設使用貪婪演演算法,有ABCDE五個選項,並兩兩組合。第一次先選D做組合,即DA、DB、DC、DE,下一次再選C做組合,這時候只用考慮CA、CB、CE,不用考慮CD,以此類推。
(3) L1正則化有什麼缺點?
有一些點被扔掉了,而且是隨機扔掉的。我們希望挑一個全域性最好的扔掉,但是它是挑一個區域性最好的扔掉。
決策樹
決策樹的定義
決策樹的分類:
1、分類決策樹 / 迴歸決策樹
2、二元樹 / 多叉樹
決策樹演演算法:
CART演演算法只能構建二元樹,其他演演算法可以構建多叉樹
有些只可以做迴歸或者分類
一顆決策樹對應的決策邊界:
需要學習:1.樹的形狀 2. 每一個決策的閾值\(\theta_1\) 3. 葉節點的值
好的特徵特點:
分類後不確定性變小
不確定性——資訊熵
事情發生的概率很低:資訊熵很高
事情發生的概率很高:資訊熵很低
log取2資訊量是位元,取1是奈特
決策樹:原來的不確定性(劃分前的)-分割後的不確定性(劃分後的)=不確定性的減小(資訊熵-條件熵=資訊增益)
資訊增益最大的作為根節點:\(f_2>f_1\),所以\(f_2\)作為根節點
問題:
(1)決策樹的根節點和葉節點代表什麼?
根節點:輸入方向;葉節點:判別指標,就是分為哪一類。也就是說,根節點是指標,最後那個葉節點是標籤。根節點是輸入,葉節點是輸出。
(2)決策樹的作用
決策樹的作用:分類和迴歸。注意:三種樹只有CART才能做迴歸。
(3)決策樹的決策邊界和線性迴歸的邊界有什麼區別?
之前線性迴歸邊界都是二分類,現在決策邊界可以包含多分類,可以有多個區域。
(4)資訊熵為什麼取對數?
避免他們之間的差距過大,比如一個概率是log0.01,另一個是log0.09。
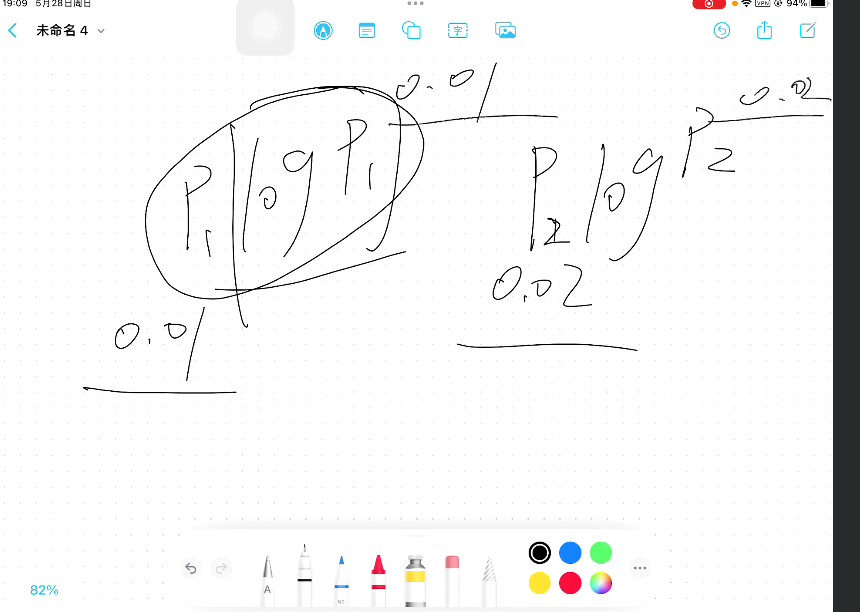
上面0.01次方和0.02次方差距會很明顯,混亂程度會加劇,從而更容易做決策。
資料處理取對數:核心是為了差距變得更大(0-1之間)或更小(1以上)
(5)資訊熵是做什麼的?
資訊熵就是在算平均資訊量。
構建決策樹
問題:
(1)特徵一樣、標籤不一樣的資料要不要刪除?
這種資料不能刪,因為這種資料會提供一定的不確定性,如果刪掉資訊熵會一下子降低,會導致結果變得很差。
(2)決策樹中唯一路徑是什麼?
給一條路徑,可以一條路走到底的。
(3)什麼是深度?
做幾次判斷,深度就有多少。最大的判斷值為樹的深度。
(4)什麼時候不用繼續分類?
一條路走到底,都是F或者都是N,就可以不用繼續分類。
(5)同一個樣本,結果既是F也是N,這是什麼情況?
同個標籤但又F和N,這條樣本是在決策邊界上,這類資料的作用是告訴你什麼地方是決策邊界。這類樣本是不能刪除的。
決策樹效能
決策樹效能:提升效能——防止過擬合,越簡單越好
如何避免決策樹的過擬合?
最大深度對模型準確率的影響
問題:
(1)決策樹過擬合有哪些原因?
-
資料不行:有用的特徵都沒有,如學習成績和他平時吃什麼。
-
特徵樣本里出現噪聲
-
某個地方資訊熵有錯誤,隨著迭代錯誤越來越放大
解決方法:
-
剪枝(修改一些葉節點)
-
設定最大深度
-
整合學習
(2)多重比較是什麼?
每次進行比較的時候都會出現錯誤,樹的深度一旦大了,會涉及到一個過多的比較過程,錯誤會越來越多,誤差也會隨之累加起來,變得越來越大。
迴歸樹如何構建
迴歸問題中量化不確定性:標準差(分類是資訊熵)
問題:
(1)迴歸樹和分類樹的區別?
計算方法:迴歸樹選擇根節點是用標準差來選,分類樹是資訊熵去選。條件熵是差不多的
(2)迴歸樹中如何確定標籤?
決策樹分裂完是同一個標籤,是或者否。而回歸樹是有一個閾值的,就是標準差小於某個數位,那麼分類就結束了。