前言

考慮到 B+ 樹較為複雜，CMU15-445 將 B+ 樹實驗拆成了兩部分，這篇部落格將介紹 Checkpoint#1 部分的實現過程，搭配教材 《DataBase System Concepts》食用更佳。

B+ 樹索引

許多查詢只涉及檔案中的少量記錄，例如「找出物理系所有教師」的查詢就只涉及教師記錄中的一小部分，如果資料庫系統讀取表中每一個元組並檢查系名稱是否為「物理」，這樣是十分低效的。理想情況下，資料庫系統應能直接定位這些記錄。為了支援這種快速存取方式，資料庫系統使用了索引。

有兩種基本的索引型別：

• 順序索引：基於值的順序排序。
• 雜湊索引：基於將值平均分佈到若干雜湊桶中。一個值所屬的雜湊桶是由一個函數決定的，該函數稱為雜湊函數(hash function)。

對於等值查詢，雜湊索引的速度最快，時間複雜度為 \(O(1)\) ，但是對於範圍查詢，雜湊索引表示無能為力。這時候順序索引就可以派上用場了，目前資料庫系統用的最多的順序索引是 B+ 樹索引，時間複雜度為 \(O(logN)\)。下圖顯示了一棵 B+ 樹，它是右下角資料表第二列的索引：

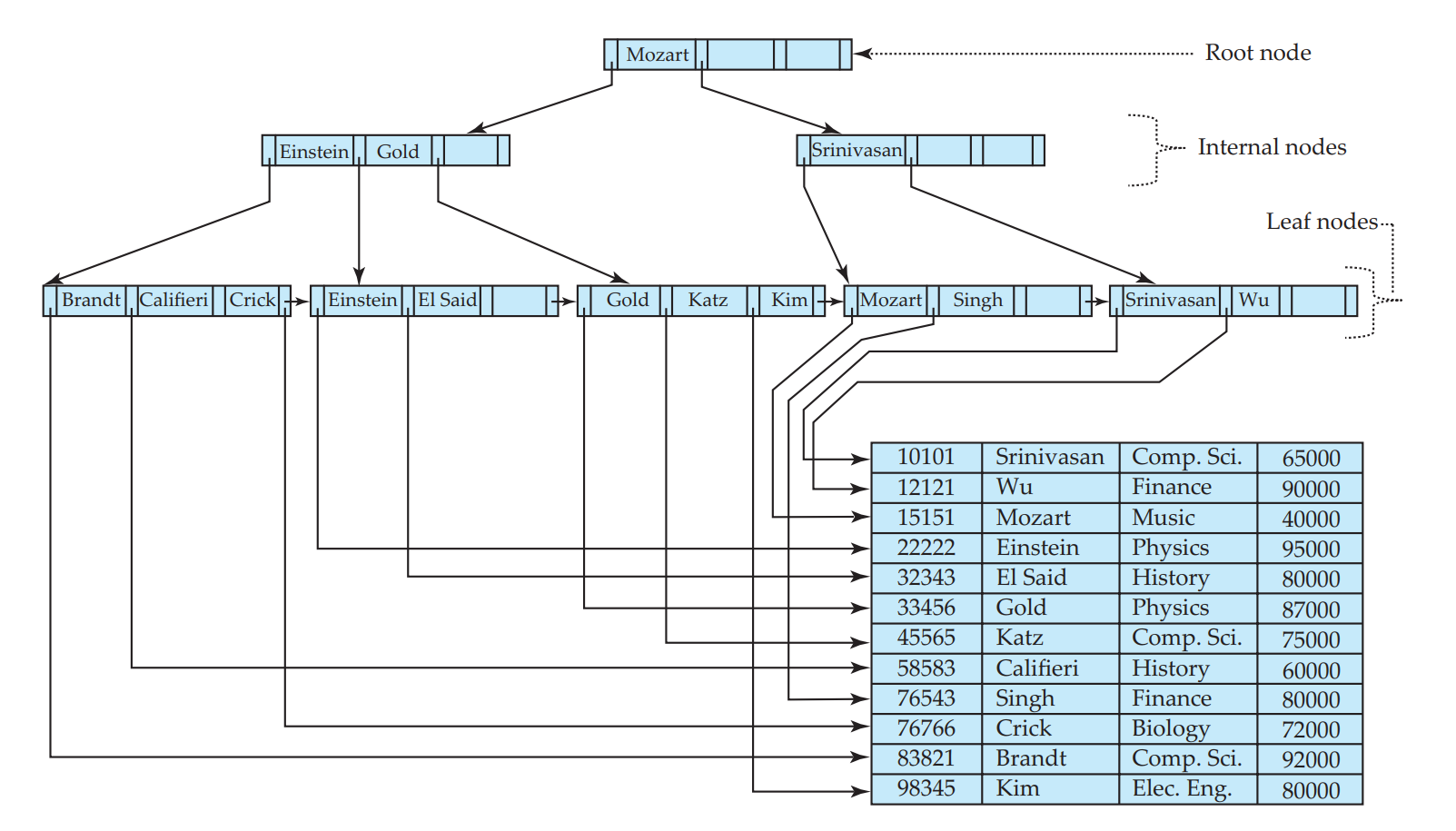
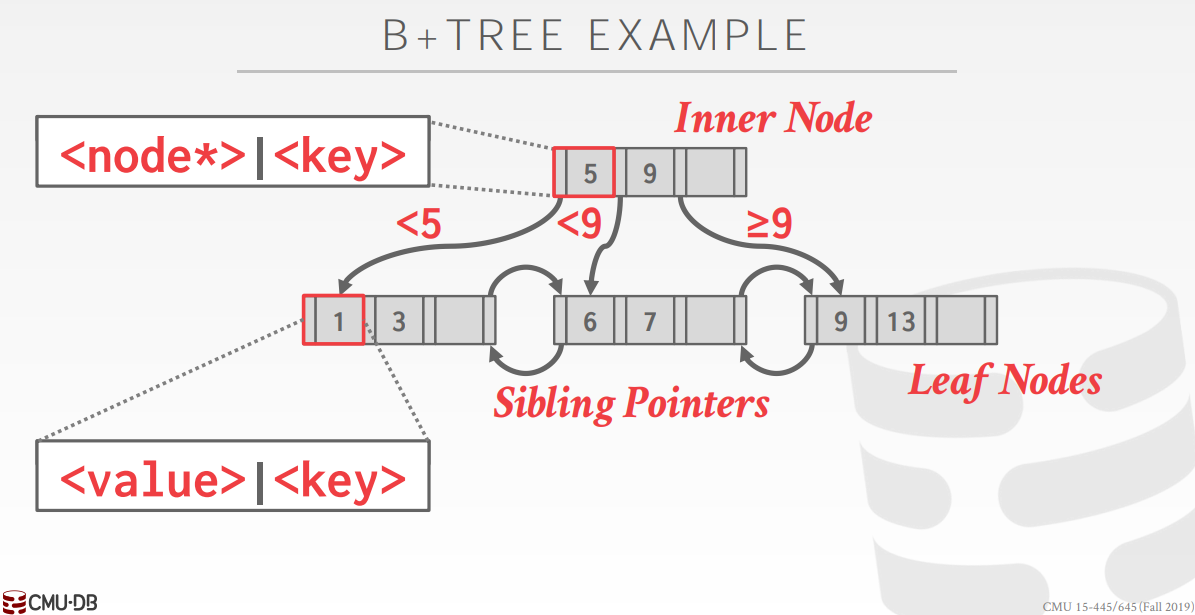
可以看到 B+ 樹是一種多路平衡搜尋樹，由葉節點和內部節點組成，其中葉節點可以儲存整條記錄或者是記錄的行 ID，內部節點只會儲存鍵和指向子節點的指標，這樣資料庫系統就能讀入更多的內部節點到記憶體中，減少磁碟 IO 次數。除了根節點外，其他節點都是至少半滿的。

程式碼實現

B+ Tree Page

B+ Tree Parent Page

B+ 樹的每個節點對應著一個 Page，內部節點對應 BPlusTreeInternalPage，葉節點對應 BPlusTreeLeafPage，這兩種頁結構相似，所以先實現父類別 BPlusTreePage，它的結構如下圖所示（圖片使用 Excalidraw 繪製）：

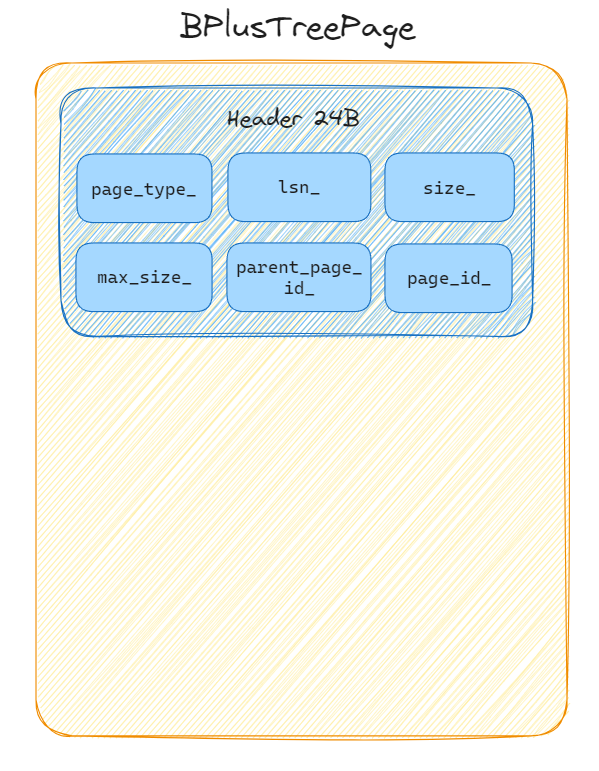
header 佔用了 24 位元組，各個欄位的大小和描述如下表所示：

Variable Name	Size	Description
page_type_	4	Page Type (internal or leaf)
lsn_	4	Log sequence number (Used in Project 4)
size_	4	Number of Key & Value pairs in page
max_size_	4	Max number of Key & Value pairs in page
parent_page_id_	4	Parent Page Id
page_id_	4	Self Page Id

BPlusTreePage 宣告如下：

#define MappingType std::pair<KeyType, ValueType>

#define INDEX_TEMPLATE_ARGUMENTS template <typename KeyType, typename ValueType, typename KeyComparator>

// define page type enum
enum class IndexPageType { INVALID_INDEX_PAGE = 0, LEAF_PAGE, INTERNAL_PAGE };

class BPlusTreePage {
 public:
  bool IsLeafPage() const;
  bool IsRootPage() const;
  void SetPageType(IndexPageType page_type);

  int GetSize() const;
  void SetSize(int size);
  void IncreaseSize(int amount);

  int GetMaxSize() const;
  void SetMaxSize(int max_size);
  int GetMinSize() const;

  page_id_t GetParentPageId() const;
  void SetParentPageId(page_id_t parent_page_id);

  page_id_t GetPageId() const;
  void SetPageId(page_id_t page_id);

  void SetLSN(lsn_t lsn = INVALID_LSN);

 private:
  IndexPageType page_type_ __attribute__((__unused__));
  lsn_t lsn_ __attribute__((__unused__));
  int size_ __attribute__((__unused__));
  int max_size_ __attribute__((__unused__));
  page_id_t parent_page_id_ __attribute__((__unused__));
  page_id_t page_id_ __attribute__((__unused__));
};

該類的實現較為簡單，但是 GetMinSize() 函數值得細細推敲。根據教材中的描述，當最大鍵值對數量為 \(N\) 時，節點的最少鍵值對數量存在三種情況：

• 根節點：
  • 根節點是葉節點時，內部至少需要 1 個鍵值對，這個很好理解，比如往空的 B+ 樹插入一個鍵值對後，新建的根節點肯定只會有一個鍵值對；
  • 根節點是內部節點是，內部至少需要 2 個鍵值對，除去最左側的無效鍵，還需要一個鍵與輸入的鍵進行比較；
• 內部節點：節點插入資料之後可能溢位，這時需要進行分裂操作，為了簡化分裂程式碼的編寫，內部節點和根節點會留出一個鍵值對的位置作為哨兵，實際最大鍵值對數量為 \(N-1\)，加上最左側的無效鍵，最小鍵值對數量為 \(\lceil (N-2)/2 \rceil+1\)；
• 葉節點：最小鍵值對數量為 \(\lceil (N-1)/2 \rceil\)

/*
 * Helper methods to get/set page type
 * Page type enum class is defined in b_plus_tree_page.h
 */
bool BPlusTreePage::IsLeafPage() const { return page_type_ == IndexPageType::LEAF_PAGE; }
bool BPlusTreePage::IsRootPage() const { return parent_page_id_ == INVALID_PAGE_ID; }
void BPlusTreePage::SetPageType(IndexPageType page_type) { page_type_ = page_type; }

/*
 * Helper methods to get/set size (number of key/value pairs stored in that
 * page)
 */
int BPlusTreePage::GetSize() const { return size_; }
void BPlusTreePage::SetSize(int size) { size_ = size; }
void BPlusTreePage::IncreaseSize(int amount) { size_ += amount; }

/*
 * Helper methods to get/set max size (capacity) of the page
 */
int BPlusTreePage::GetMaxSize() const { return max_size_; }
void BPlusTreePage::SetMaxSize(int size) { max_size_ = size; }

/*
 * Helper method to get min page size
 * Generally, min page size == max page size / 2
 */
int BPlusTreePage::GetMinSize() const {
  // 資料庫系統概念中文第六版 Page #486
  // 葉節點最少有一個鍵，而內部節點除了無效的第一個鍵外還需一個鍵
  if (IsRootPage()) {
    return IsLeafPage() ? 1 : 2;
  }

  // 內部節點的最小鍵值對數量為 ⌈(max_size_ - 1 - 1)/2⌉ + 1
  if (!IsLeafPage()) {
    return (max_size_ - 2 + 1) / 2 + 1;
  }

  // 葉節點最小鍵值對數量為 ⌈(max_size_ - 1)/2⌉
  return (max_size_ - 1 + 1) / 2;
}

/*
 * Helper methods to get/set parent page id
 */
page_id_t BPlusTreePage::GetParentPageId() const { return parent_page_id_; }
void BPlusTreePage::SetParentPageId(page_id_t parent_page_id) { parent_page_id_ = parent_page_id; }

/*
 * Helper methods to get/set self page id
 */
page_id_t BPlusTreePage::GetPageId() const { return page_id_; }
void BPlusTreePage::SetPageId(page_id_t page_id) { page_id_ = page_id; }

/*
 * Helper methods to set lsn
 */
void BPlusTreePage::SetLSN(lsn_t lsn) { lsn_ = lsn; }

B+ Tree Internal Page

內部節點頁的結構如下圖所示，它比父類別多了一個 array 陣列成員，用於存放 key | page_id 鍵值對，其中 page_id 是子節點的頁 id：

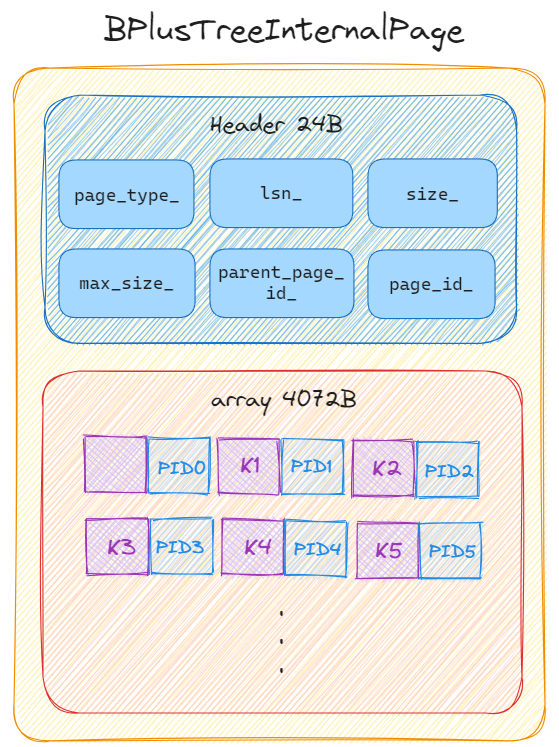
，宣告如下述程式碼所示。可以看到 array 的長度宣告為 0，這種寫法比較神奇，它的意思是 array 的實際長度是在執行時確定的。實驗一中我們實現了緩衝池管理器，用於快取 Page，而節點頁就存放在 char Page::data_[PAGE_SIZE] 中，當 PAGE_SIZE 為 4096 位元組時，array 最多能放 INTERNAL_PAGE_SIZE 個鍵值對：

#define B_PLUS_TREE_INTERNAL_PAGE_TYPE BPlusTreeInternalPage<KeyType, ValueType, KeyComparator>
#define INTERNAL_PAGE_HEADER_SIZE 24
#define INTERNAL_PAGE_SIZE ((PAGE_SIZE - INTERNAL_PAGE_HEADER_SIZE) / (sizeof(MappingType)))
/**
 * Store n indexed keys and n+1 child pointers (page_id) within internal page.
 * Pointer PAGE_ID(i) points to a subtree in which all keys K satisfy:
 * K(i) <= K < K(i+1).
 * NOTE: since the number of keys does not equal to number of child pointers,
 * the first key always remains invalid. That is to say, any search/lookup
 * should ignore the first key.
 */
INDEX_TEMPLATE_ARGUMENTS
class BPlusTreeInternalPage : public BPlusTreePage {
 public:
  void Init(page_id_t page_id, page_id_t parent_id = INVALID_PAGE_ID, int max_size = INTERNAL_PAGE_SIZE);

  KeyType KeyAt(int index) const;
  void SetKeyAt(int index, const KeyType &key);
  int ValueIndex(const ValueType &value) const;
  ValueType ValueAt(int index) const;

  ValueType Lookup(const KeyType &key, const KeyComparator &comparator) const;
  void PopulateNewRoot(const ValueType &old_value, const KeyType &new_key, const ValueType &new_value);
  int InsertNodeAfter(const ValueType &old_value, const KeyType &new_key, const ValueType &new_value);
  void Remove(int index);
  ValueType RemoveAndReturnOnlyChild();

  // Split and Merge utility methods
  void MoveAllTo(BPlusTreeInternalPage *recipient, const KeyType &middle_key, BufferPoolManager *buffer_pool_manager);
  void MoveHalfTo(BPlusTreeInternalPage *recipient, BufferPoolManager *buffer_pool_manager);

 private:
  void CopyNFrom(MappingType *items, int size, BufferPoolManager *buffer_pool_manager);
  MappingType array[0];
};

先來實現幾個簡單的函數，其中 Init() 函數必須在內部節點頁在緩衝池中被建立出來後呼叫：

/*
 * Init method after creating a new internal page
 * Including set page type, set current size, set page id, set parent id and set max page size
 */
INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_INTERNAL_PAGE_TYPE::Init(page_id_t page_id, page_id_t parent_id, int max_size) {
  SetPageType(IndexPageType::INTERNAL_PAGE);
  SetSize(0);
  SetPageId(page_id);
  SetParentPageId(parent_id);
  SetMaxSize(max_size);
}

/*
 * Helper method to get/set the key associated with input "index"(a.k.a array offset)
 */
INDEX_TEMPLATE_ARGUMENTS
KeyType B_PLUS_TREE_INTERNAL_PAGE_TYPE::KeyAt(int index) const { return array[index].first; }

INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_INTERNAL_PAGE_TYPE::SetKeyAt(int index, const KeyType &key) { array[index].first = key; }

/*
 * Helper method to find and return array index(or offset), so that its value equals to input "value"
 */
INDEX_TEMPLATE_ARGUMENTS
int B_PLUS_TREE_INTERNAL_PAGE_TYPE::ValueIndex(const ValueType &value) const {
  for (int i = 0; i < GetSize(); ++i) {
    if (ValueAt(i) == value) {
      return i;
    }
  }
  return -1;
}

/*
 * Helper method to get the value associated with input "index"(a.k.a array offset)
 */
INDEX_TEMPLATE_ARGUMENTS
ValueType B_PLUS_TREE_INTERNAL_PAGE_TYPE::ValueAt(int index) const { return array[index].second; }

B+ Tree Leaf Page

BPlusTreeLeafPage 的結構和 BPlusTreeInternalPage 相似，只是在 header 區域多了一個 next_page_id_ 欄位，該欄位是下一個葉節點的指標，用於將葉節點串成單向連結串列。同時 array 內部鍵值對存放的是 key | RID，指向實際資料的位置。

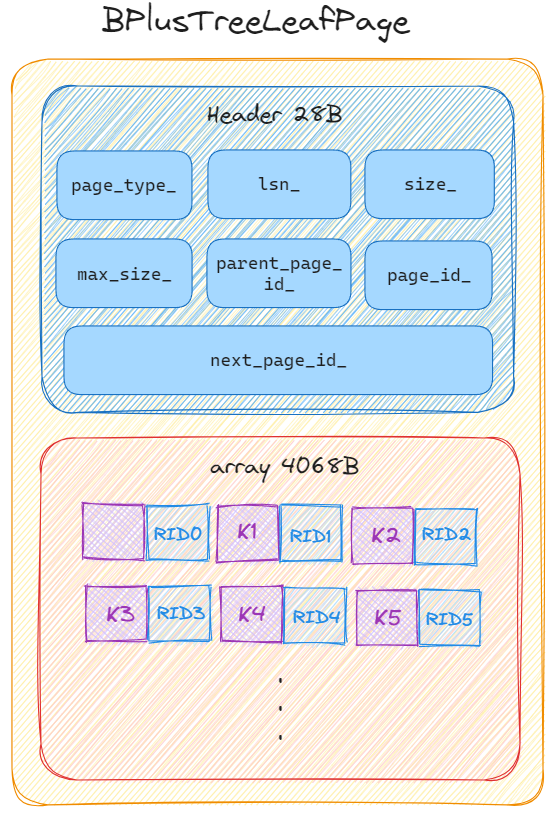
類宣告如下：

#define B_PLUS_TREE_LEAF_PAGE_TYPE BPlusTreeLeafPage<KeyType, ValueType, KeyComparator>
#define LEAF_PAGE_HEADER_SIZE 28
#define LEAF_PAGE_SIZE ((PAGE_SIZE - LEAF_PAGE_HEADER_SIZE) / sizeof(MappingType))

/**
 * Store indexed key and record id(record id = page id combined with slot id,
 * see include/common/rid.h for detailed implementation) together within leaf
 * page. Only support unique key.
 */
INDEX_TEMPLATE_ARGUMENTS
class BPlusTreeLeafPage : public BPlusTreePage {
 public:
  void Init(page_id_t page_id, page_id_t parent_id = INVALID_PAGE_ID, int max_size = LEAF_PAGE_SIZE);
  // helper methods
  page_id_t GetNextPageId() const;
  void SetNextPageId(page_id_t next_page_id);
  KeyType KeyAt(int index) const;
  int KeyIndex(const KeyType &key, const KeyComparator &comparator) const;
  const MappingType &GetItem(int index);

  // insert and delete methods
  int Insert(const KeyType &key, const ValueType &value, const KeyComparator &comparator);
  bool Lookup(const KeyType &key, ValueType *value, const KeyComparator &comparator) const;
  int RemoveAndDeleteRecord(const KeyType &key, const KeyComparator &comparator);

  // Split and Merge utility methods
  void MoveHalfTo(BPlusTreeLeafPage *recipient, BufferPoolManager *buffer_pool_manager);
  void MoveAllTo(BPlusTreeLeafPage *recipient);
  void MoveFirstToEndOf(BPlusTreeLeafPage *recipient);
  void MoveLastToFrontOf(BPlusTreeLeafPage *recipient);

 private:
  void CopyNFrom(MappingType *items, int size);
  page_id_t next_page_id_;
  MappingType array[0];
};

先來實現幾個簡單的函數：

/**
 * Init method after creating a new leaf page
 * Including set page type, set current size to zero, set page id/parent id, set next page id and set max size
 */
INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_LEAF_PAGE_TYPE::Init(page_id_t page_id, page_id_t parent_id, int max_size) {
  SetPageType(IndexPageType::LEAF_PAGE);
  SetSize(0);
  SetPageId(page_id);
  SetParentPageId(parent_id);
  SetNextPageId(INVALID_PAGE_ID);
  SetMaxSize(max_size);
}

/**
 * Helper methods to set/get next page id
 */
INDEX_TEMPLATE_ARGUMENTS
page_id_t B_PLUS_TREE_LEAF_PAGE_TYPE::GetNextPageId() const { return next_page_id_; }

INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_LEAF_PAGE_TYPE::SetNextPageId(page_id_t next_page_id) { next_page_id_ = next_page_id; }

/*
 * Helper method to find and return the key associated with input "index"(a.k.a array offset)
 */
INDEX_TEMPLATE_ARGUMENTS
KeyType B_PLUS_TREE_LEAF_PAGE_TYPE::KeyAt(int index) const { return array[index].first; }

/*
 * Helper method to find and return the key & value pair associated with input "index"(a.k.a array offset)
 */
INDEX_TEMPLATE_ARGUMENTS
const MappingType &B_PLUS_TREE_LEAF_PAGE_TYPE::GetItem(int index) { return array[index]; }

至此可以畫出整棵 B+ 樹的結構：

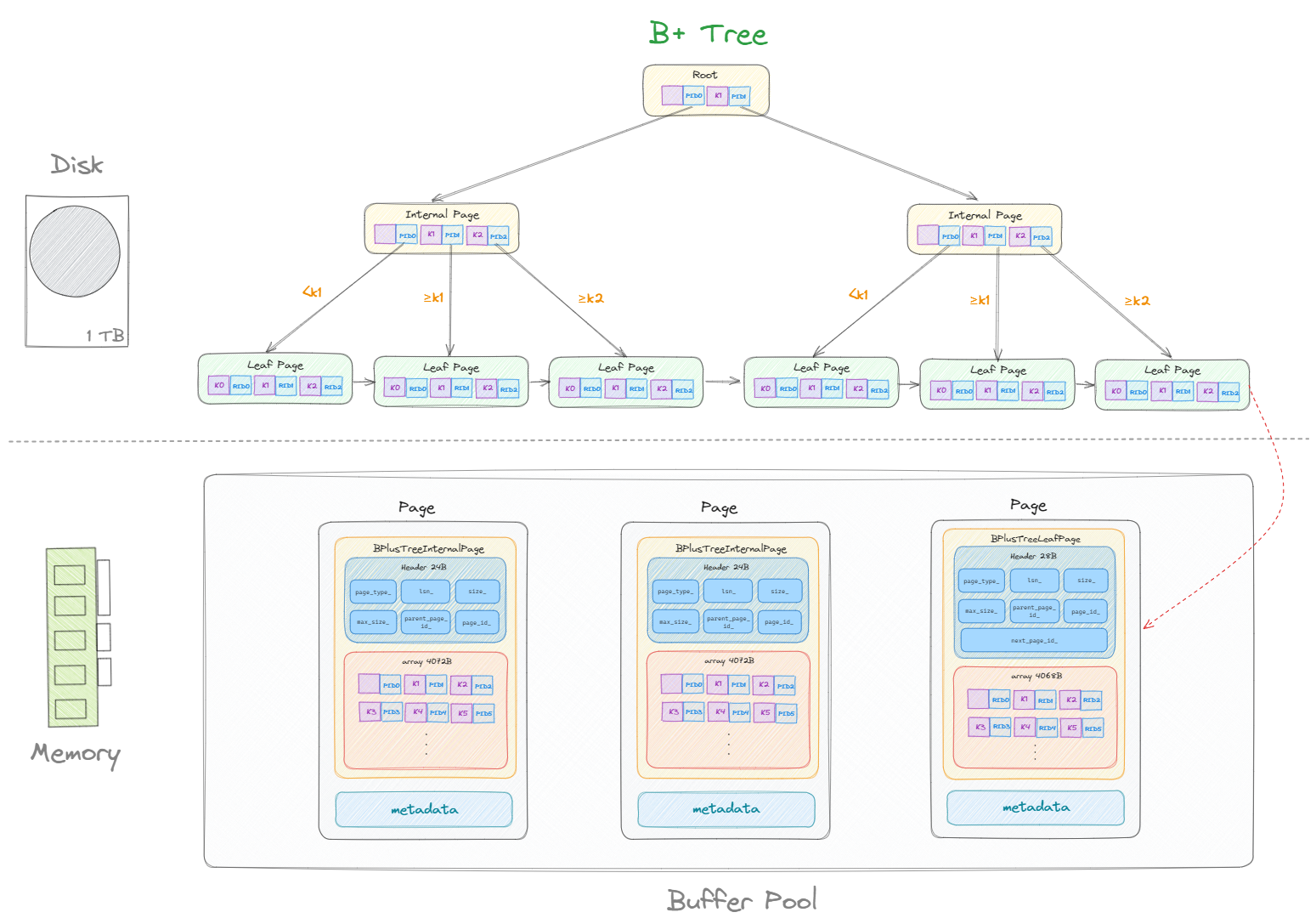
B+ Tree 查詢

B+ 樹的搜尋較為簡單，先從根節點開始，將內部節點與搜尋的 key 進行二分搜尋，找出包含 key 的子節點的指標，然後向緩衝池要子節點頁，接著在子節點上重複上述過程直到葉節點為止，最後在葉節點上進行二分搜尋。

/**
 * Return the only value that associated with input key
 * This method is used for point query
 * @return : true means key exists
 */
INDEX_TEMPLATE_ARGUMENTS
bool BPLUSTREE_TYPE::GetValue(const KeyType &key, std::vector<ValueType> *result, Transaction *transaction) {
  if (IsEmpty()) {
    return false;
  }

  // 在葉節點中尋找 key
  LeafPage *leaf = ToLeafPage(FindLeafPage(key));

  ValueType value;
  auto success = leaf->Lookup(key, &value, comparator_);
  if (success) {
    result->push_back(value);
  }

  buffer_pool_manager_->UnpinPage(leaf->GetPageId(), false);
  return success;
}

/*
 * Helper function to decide whether current b+tree is empty
 */
INDEX_TEMPLATE_ARGUMENTS
bool BPLUSTREE_TYPE::IsEmpty() const { return root_page_id_ == INVALID_PAGE_ID; }

/**
 * Find leaf page containing particular key, if leftMost flag == true, find
 * the left most leaf page
 */
INDEX_TEMPLATE_ARGUMENTS
Page *BPLUSTREE_TYPE::FindLeafPage(const KeyType &key, bool leftMost) {
  auto page_id = root_page_id_;
  auto page = buffer_pool_manager_->FetchPage(page_id);
  if (!page) {
    return nullptr;
  }

  // 定位到包含 key 的葉節點
  auto node = ToTreePage(page);
  while (!node->IsLeafPage()) {
    InternalPage *inode = ToInternalPage(node);

    // 尋找下一個包含 key 的節點
    if (!leftMost) {
      page_id = inode->Lookup(key, comparator_);
    } else {
      page_id = inode->ValueAt(0);
    }

    // 移動到子節點
    buffer_pool_manager_->UnpinPage(page->GetPageId(), false);
    page = buffer_pool_manager_->FetchPage(page_id);
    node = ToTreePage(page);
  }

  return page;
}

由於經常要進行 Page –> BPlusTreePage –> BPlusTreeLeafPage/BplusTreeInternalPage 的轉換，所以在類宣告內部新增了幾個轉換函數：

BPlusTreePage *ToTreePage(Page *page) { return reinterpret_cast<BPlusTreePage *>(page->GetData()); }
InternalPage *ToInternalPage(Page *page) { return reinterpret_cast<InternalPage *>(page->GetData()); }
LeafPage *ToLeafPage(Page *page) { return reinterpret_cast<LeafPage *>(page->GetData()); }

InternalPage *ToInternalPage(BPlusTreePage *page) { return reinterpret_cast<InternalPage *>(page); }
LeafPage *ToLeafPage(BPlusTreePage *page) { return reinterpret_cast<LeafPage *>(page); }

內部節點二分查詢 InternalPage::LoopUp() 的實現如下所示，這裡使用了一種大一統的二分查詢寫法，無需考慮索引是否加減 1 的問題以及 left 和 right 指標比較的時候要不要加等號的問題，只要寫好分割區條件就行，非常好用，牆裂推薦花幾分鐘看下 B 站的這個教學「二分查詢為什麼總是寫錯？」。

因為第一個鍵無效，所以 left 的初始值為 0，而將索引分給 left 區域的條件就是 KeyAt(mid) 小於等於 key，這樣迴圈結束的時候 left 對應的就是最後一個小於等於 key 的鍵，指標指向的子節點必包含 key：

/*
 * Find and return the child pointer(page_id) which points to the child page
 * that contains input "key"
 * Start the search from the second key(the first key should always be invalid)
 */
INDEX_TEMPLATE_ARGUMENTS
ValueType B_PLUS_TREE_INTERNAL_PAGE_TYPE::Lookup(const KeyType &key, const KeyComparator &comparator) const {
  // 二分查詢大一統寫法：https://www.bilibili.com/video/BV1d54y1q7k7/
  int left = 0, right = GetSize();
  while (left + 1 < right) {
    int mid = left + (right - left) / 2;
    if (comparator(KeyAt(mid), key) <= 0) {
      left = mid;
    } else {
      right = mid;
    }
  }
  return ValueAt(left);
}

葉節點二分查詢的程式碼為：

/*
 * For the given key, check to see whether it exists in the leaf page. If it
 * does, then store its corresponding value in input "value" and return true.
 * If the key does not exist, then return false
 */
INDEX_TEMPLATE_ARGUMENTS
bool B_PLUS_TREE_LEAF_PAGE_TYPE::Lookup(const KeyType &key, ValueType *value, const KeyComparator &comparator) const {
  int left = 0, right = GetSize() - 1;
  while (left <= right) {
    int mid = left + (right - left) / 2;
    int cmp = comparator(KeyAt(mid), key);
    if (cmp == 0) {
      *value = array[mid].second;
      return true;
    } else if (cmp > 0) {
      right = mid - 1;
    } else {
      left = mid + 1;
    }
  }
  return false;
}

B+ Tree 插入

B+ 樹的插入較為複雜，定位到需要插入的葉節點後需要考慮節點溢位的問題，可以在這個演演算法視覺化網站檢視 B+ 樹的插入過程。教材中給出了插入演演算法的虛擬碼：

總體流程就是先判斷樹是否為空，如果是空的就新建一個葉節點作為根節點並插入鍵值對，否則將鍵值對插到對應的葉節點 \(N\) 中：

/**
 * Insert constant key & value pair into b+ tree
 * if current tree is empty, start new tree, update root page id and insert
 * entry, otherwise insert into leaf page.
 * @return: since we only support unique key, if user try to insert duplicate
 * keys return false, otherwise return true.
 */
INDEX_TEMPLATE_ARGUMENTS
bool BPLUSTREE_TYPE::Insert(const KeyType &key, const ValueType &value, Transaction *transaction) {
  if (!IsEmpty()) {
    return InsertIntoLeaf(key, value, transaction);
  }

  StartNewTree(key, value);
  return true;
}

/**
 * Insert constant key & value pair into an empty tree
 * User needs to first ask for new page from buffer pool manager(NOTICE: throw
 * an "out of memory" exception if returned value is nullptr), then update b+
 * tree's root page id and insert entry directly into leaf page.
 */
INDEX_TEMPLATE_ARGUMENTS
void BPLUSTREE_TYPE::StartNewTree(const KeyType &key, const ValueType &value) {
  // 建立一個葉節點作為根節點，並插入新資料
  LeafPage *root = ToLeafPage(NewPage(&root_page_id_));
  root->Init(root_page_id_, INVALID_PAGE_ID, leaf_max_size_);
  root->Insert(key, value, comparator_);

  UpdateRootPageId(1);
  buffer_pool_manager_->UnpinPage(root_page_id_, true);
}

INDEX_TEMPLATE_ARGUMENTS
Page *BPLUSTREE_TYPE::NewPage(page_id_t *page_id) {
  auto page = buffer_pool_manager_->NewPage(page_id);
  if (!page) {
    throw Exception(ExceptionType::OUT_OF_MEMORY, "Can't create new page");
  }

  return page;
}

如果葉節點 \(N\) 沒有滿，那麼直接插入就行，否則需要對葉節點 \(N\) 進行分裂操作：

1. 在緩衝池中新建一個頁為葉節點 \(N'\)；
2. 將 \(N\) 的右半部分鍵值對移動到 \(N'\) 中，並更新 next_page_id_ 指標；
3. 將 \(N'\) 最左側的鍵 \(K'\) 和 \(N'\) 的指標插到 \(N\) 的父節點中

對應程式碼為：

/**
 * Insert constant key & value pair into leaf page
 * User needs to first find the right leaf page as insertion target, then look
 * through leaf page to see whether insert key exist or not. If exist, return
 * immdiately, otherwise insert entry. Remember to deal with split if necessary.
 * @return: since we only support unique key, if user try to insert duplicate
 * keys return false, otherwise return true.
 */
INDEX_TEMPLATE_ARGUMENTS
bool BPLUSTREE_TYPE::InsertIntoLeaf(const KeyType &key, const ValueType &value, Transaction *transaction) {
  // 定位到包含 key 的葉節點
  LeafPage *leaf = ToLeafPage(FindLeafPage(key));

  // 不能插入相同的鍵
  ValueType exist_value;
  if (leaf->Lookup(key, &exist_value, comparator_)) {
    buffer_pool_manager_->UnpinPage(leaf->GetPageId(), false);
    return false;
  }

  // 如果葉節點沒有滿，就直接插進去（array 最後留了一個空位），否則分裂葉節點並更新父節點
  auto size = leaf->Insert(key, value, comparator_);

  if (size == leaf_max_size_) {
    LeafPage *new_leaf = Split(leaf);
    InsertIntoParent(leaf, new_leaf->KeyAt(0), new_leaf, transaction);
    buffer_pool_manager_->UnpinPage(new_leaf->GetPageId(), true);
  }

  buffer_pool_manager_->UnpinPage(leaf->GetPageId(), true);
  return true;
}

/**
 * Split input page and return newly created page.
 * Using template N to represent either internal page or leaf page.
 * User needs to first ask for new page from buffer pool manager(NOTICE: throw
 * an "out of memory" exception if returned value is nullptr), then move half
 * of key & value pairs from input page to newly created page
 */
INDEX_TEMPLATE_ARGUMENTS
template <typename N>
N *BPLUSTREE_TYPE::Split(N *node) {
  // 建立新節點
  page_id_t new_page_id;
  auto new_page = NewPage(&new_page_id);
  N *new_node = reinterpret_cast<N *>(new_page->GetData());

  // 將右半邊的 item 移動到新節點中
  auto max_size = node->IsLeafPage() ? leaf_max_size_ : internal_max_size_;
  new_node->Init(new_page_id, node->GetParentPageId(), max_size);
  node->MoveHalfTo(new_node, buffer_pool_manager_);

  return new_node;
}

之前提到過，節點留了一個鍵值對的位置充當哨兵，這樣當內部鍵值對數量達到 max_size_ - 1 時，可以把新的鍵值對插進去而不用像虛擬碼中說的那樣在記憶體中開闢一塊能夠容納 max_size_ + 1 個鍵值對的空間。

插入之前需要先定位到第一個大於等於 key 的鍵值對位置，同樣可以使用大一統寫法的二分查詢做到這一點：

/*
 * Insert key & value pair into leaf page ordered by key
 * @return  page size after insertion
 */
INDEX_TEMPLATE_ARGUMENTS
int B_PLUS_TREE_LEAF_PAGE_TYPE::Insert(const KeyType &key, const ValueType &value, const KeyComparator &comparator) {
  // 獲取第一個大於等於 key 的索引並將之後的鍵值對右移
  auto index = KeyIndex(key, comparator);
  std::copy_backward(array + index, array + GetSize(), array + GetSize() + 1);

  array[index] = {key, value};
  IncreaseSize(1);
  return GetSize();
}

/**
 * Helper method to find the first index i so that array[i].first >= key
 * NOTE: This method is only used when generating index iterator
 */
INDEX_TEMPLATE_ARGUMENTS
int B_PLUS_TREE_LEAF_PAGE_TYPE::KeyIndex(const KeyType &key, const KeyComparator &comparator) const {
  // 二分查詢大一統寫法：https://www.bilibili.com/video/BV1d54y1q7k7/
  int left = -1, right = GetSize();
  while (left + 1 < right) {
    int mid = left + (right - left) / 2;
    if (comparator(KeyAt(mid), key) < 0) {
      left = mid;
    } else {
      right = mid;
    }
  }
  return right;
}

葉節點使用 MoveHalfTo() 函數進行右半部分鍵值對的移動操作，這個函數的簽名和初始程式碼不太一樣，多加了一個 buffer_pool_manager 引數：

/*
 * Remove half of key & value pairs from this page to "recipient" page
 */
INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_LEAF_PAGE_TYPE::MoveHalfTo(BPlusTreeLeafPage *recipient,
                                            __attribute__((unused)) BufferPoolManager *buffer_pool_manager) {
  int start = GetMinSize();
  int N = GetSize() - start;
  recipient->CopyNFrom(array + start, N);

  // 更新下一個頁 id
  recipient->SetNextPageId(GetNextPageId());
  SetNextPageId(recipient->GetPageId());

  IncreaseSize(-N);
}

/*
 * Copy starting from items, and copy {size} number of elements into me.
 */
INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_LEAF_PAGE_TYPE::CopyNFrom(MappingType *items, int size) {
  std::copy(items, items + size, array + GetSize());
  IncreaseSize(size);
}

父節點的插入演演算法較為複雜，如果父節點插入子節點傳來的鍵值對之後也溢位了，需要進行分裂，並將新分裂出來的父節點的最左側無效鍵和自己的指標插入父節點中。如果分裂的是根節點，需要新建根節點，之前的根節點變成內部節點，並將樹的高度 +1。

/**
 * Insert key & value pair into internal page after split
 * @param   old_node      input page from split() method
 * @param   key
 * @param   new_node      returned page from split() method
 * User needs to first find the parent page of old_node, parent node must be
 * adjusted to take info of new_node into account. Remember to deal with split
 * recursively if necessary.
 */
INDEX_TEMPLATE_ARGUMENTS
void BPLUSTREE_TYPE::InsertIntoParent(BPlusTreePage *old_node, const KeyType &key, BPlusTreePage *new_node,
                                      Transaction *transaction) {
  // 根節點發生分裂需要新建一個根節點，B+樹的高度 +1
  if (old_node->IsRootPage()) {
    auto root_page = NewPage(&root_page_id_);

    // 建立新節點並更新子節點指標
    InternalPage *root = ToInternalPage(root_page);
    root->Init(root_page_id_, INVALID_PAGE_ID, internal_max_size_);
    root->PopulateNewRoot(old_node->GetPageId(), key, new_node->GetPageId());

    // 更新父節點指標
    old_node->SetParentPageId(root_page_id_);
    new_node->SetParentPageId(root_page_id_);

    UpdateRootPageId(0);
    buffer_pool_manager_->UnpinPage(root_page_id_, true);
    return;
  }

  // 找到父節點並將新節點的最左側 key 插入其中
  auto parent_id = old_node->GetParentPageId();
  InternalPage *parent = ToInternalPage(buffer_pool_manager_->FetchPage(parent_id));
  auto size = parent->InsertNodeAfter(old_node->GetPageId(), key, new_node->GetPageId());

  // 父節點溢位時需要再次分裂
  if (size == internal_max_size_) {
    InternalPage *new_page = Split(parent);
    InsertIntoParent(parent, new_page->KeyAt(0), new_page, transaction);
    buffer_pool_manager_->UnpinPage(new_page->GetPageId(), true);
  }

  buffer_pool_manager_->UnpinPage(parent_id, true);
}

內部節點分裂的程式碼為：

/*
 * Populate new root page with old_value + new_key & new_value
 * When the insertion cause overflow from leaf page all the way upto the root
 * page, you should create a new root page and populate its elements.
 * NOTE: This method is only called within InsertIntoParent()(b_plus_tree.cpp)
 */
INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_INTERNAL_PAGE_TYPE::PopulateNewRoot(const ValueType &old_value, const KeyType &new_key,
                                                     const ValueType &new_value) {
  array[0].second = old_value;
  array[1] = {new_key, new_value};
  SetSize(2);
}

/*
 * Insert new_key & new_value pair right after the pair with its value == old_value
 * @return:  new size after insertion
 */
INDEX_TEMPLATE_ARGUMENTS
int B_PLUS_TREE_INTERNAL_PAGE_TYPE::InsertNodeAfter(const ValueType &old_value, const KeyType &new_key,
                                                    const ValueType &new_value) {
  // 找到 old_value 的位置並將後面的 item 後移一格
  auto index = ValueIndex(old_value) + 1;
  std::copy_backward(array + index, array + GetSize(), array + GetSize() + 1);

  array[index] = {new_key, new_value};
  IncreaseSize(1);
  return GetSize();
}

/*
 * Remove half of key & value pairs from this page to "recipient" page
 */
INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_INTERNAL_PAGE_TYPE::MoveHalfTo(BPlusTreeInternalPage *recipient,
                                                BufferPoolManager *buffer_pool_manager) {
  // 第一個 key 本來就沒有用，所以直接拷貝過來也沒關係
  auto start = GetMinSize();
  int N = GetSize() - start;
  recipient->CopyNFrom(array + start, N, buffer_pool_manager);
  IncreaseSize(-N);
}

測試

在終端輸入：

cd build
cmake ..
make

# 繪製 B+ 樹的工具
make b_plus_tree_print_test
./test/b_plus_tree_print_test

# 從 grading scope 拔下來的測試程式碼
make b_plus_tree_checkpoint_1_test
./test/b_plus_tree_checkpoint_1_test

繪製 B+ 樹的工具執行效果如下：

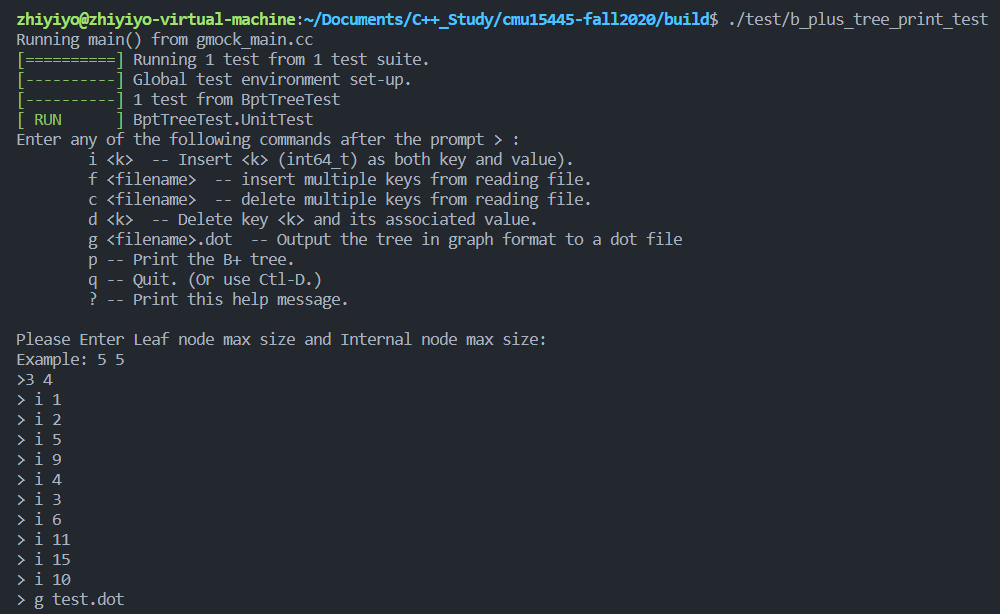
在 VSCode 中安裝一個 Dot 檔案檢視器就能看到效果了：

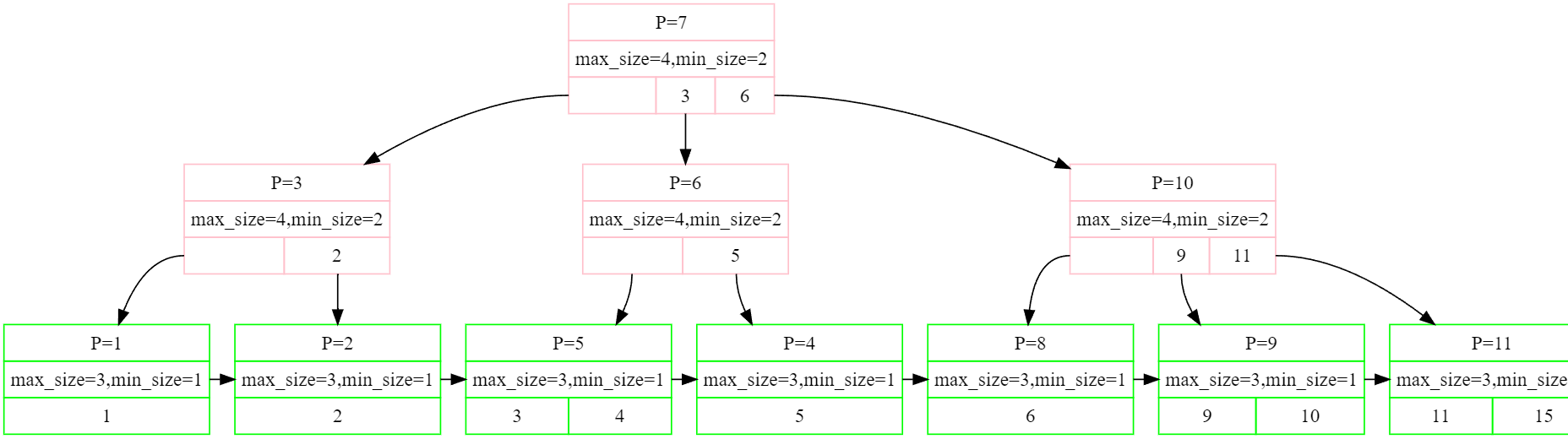
grade scope 的測試結果如下，順利通過了 4 個測試用例：

後記

這次實驗實現了單執行緒 B+ 樹的查詢和插入操作，難度相比於實驗一有了質的提升，寫完之後成就感十足，可能這也是 Andy 將實驗二拆成兩部分的原因之一吧，下個實驗就要實現二元樹的刪除操作和並行了，期待一波~~