《資料結構與演演算法》之佇列與連結串列複習
導言:
我們在上一次學習了堆疊的資料結構以後,可以瞭解到它是受限制的操作,比如我們操作只能在棧頂,現在我們要學習的東西叫做佇列,它也是受限制的一種資料結構,它的特點是隊頭只出資料,而隊尾只入資料,
它的結構就和它的名字,像我們平時排隊一樣先來的人肯定要先服務啊,所以它的英文叫做Frist In Frist Out 即 FIFO
一.順序表實現佇列
佇列:具有一定約束的線性表
插入和刪除操作:只能在一段插入,只能在另一端刪除
實現佇列我們需要根據它的特點來構建結構,比如它需要一個指標 front 指向隊頭,也需要一個指標 rear 指向隊尾
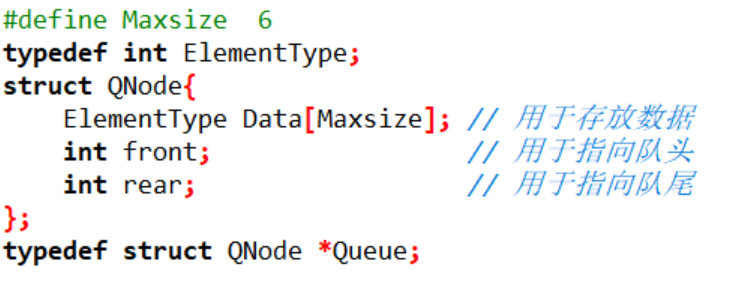
這就是我們構建的主要的結構,用它構造的陣列具有指向性,可以知道現在在哪裡可以插入資料,在哪可以刪除資料,都是實時記錄位置的
我們來思考一下現在這麼構造的資料結構,
首先,此佇列能存放6個資料,然後它在用Data來記錄真實的資料,使用font來記錄隊頭,每次出佇列都需要我們font指標向後移動一次,地址指標加一,同時使用rear來記錄隊尾,每次入隊都在這裡,它會在加一的情況後在進行入隊
隊頭指向的多是空資料,而隊尾指向的是新添的當前資料,它們指向的位置不一樣,也就是說,一旦front指向的資料,如果此空間有資料,那麼一定是出佇列的,而rear指向的空間,一定是剛剛入隊的資料
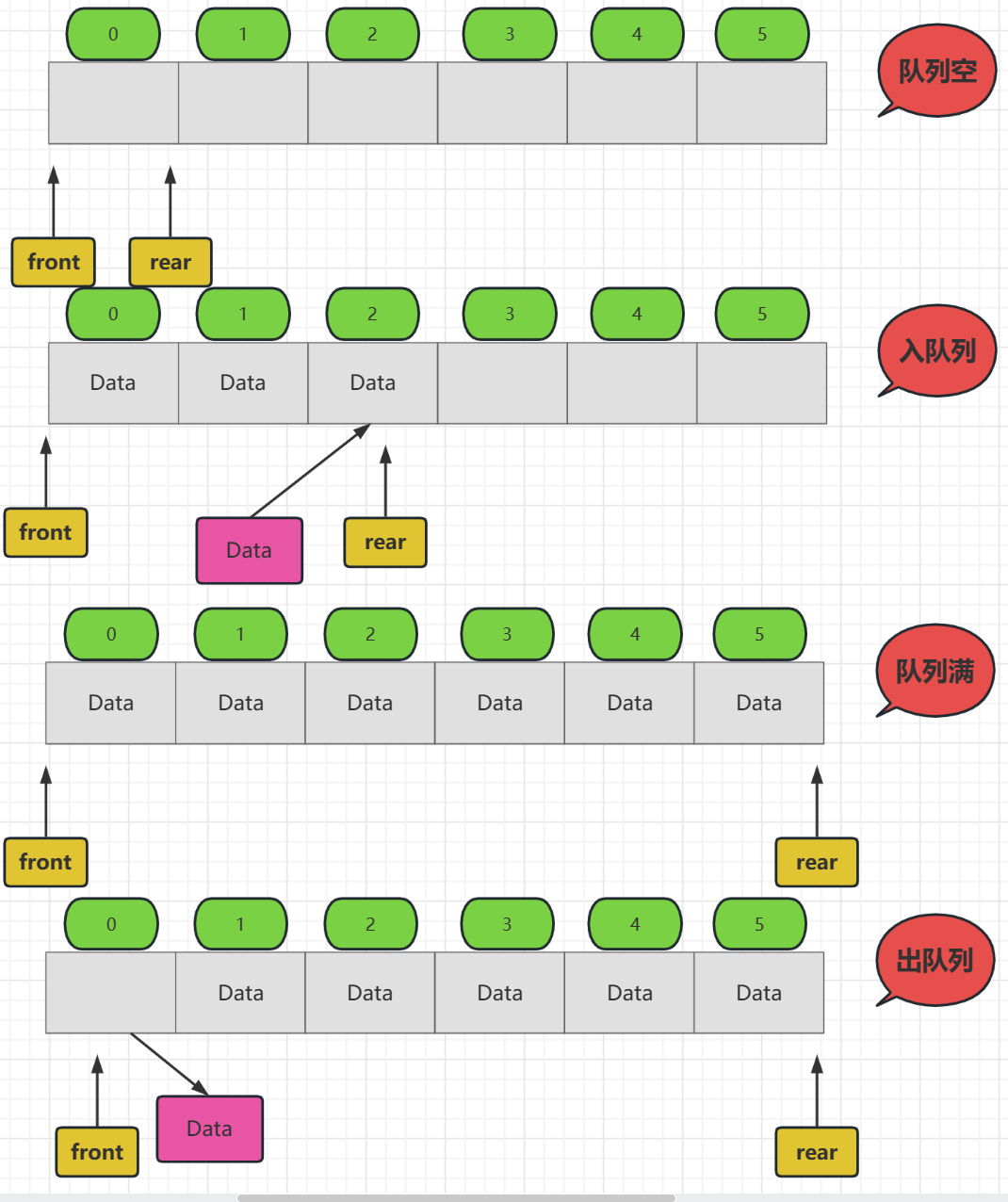
上面就是最開始我們設計的順序表實現佇列,看起來也十分簡單,完美的利用了陣列的特性,可是我們多使用幾次就會發現,他有一個很明顯的弊端,那就是經過幾次入佇列後會出現空間利用不充分的
比如我們在佇列滿了的情況下出佇列幾個資料,那麼還能入佇列嗎?很顯然不能,因為此時隊尾指標 rear 已經指向 Maxsize 了,
所以,一般我們不會使用這種方式實現佇列,空間利用率太低了,而是採用迴圈佇列的方式去構造,別入rear到達Maxsize的時候,只要發現front不在 0 號位置,說明前面還有空間可以入隊,就在前面入隊
只要front和rear指標正常工作,迴圈佇列是可以很簡單的實現的
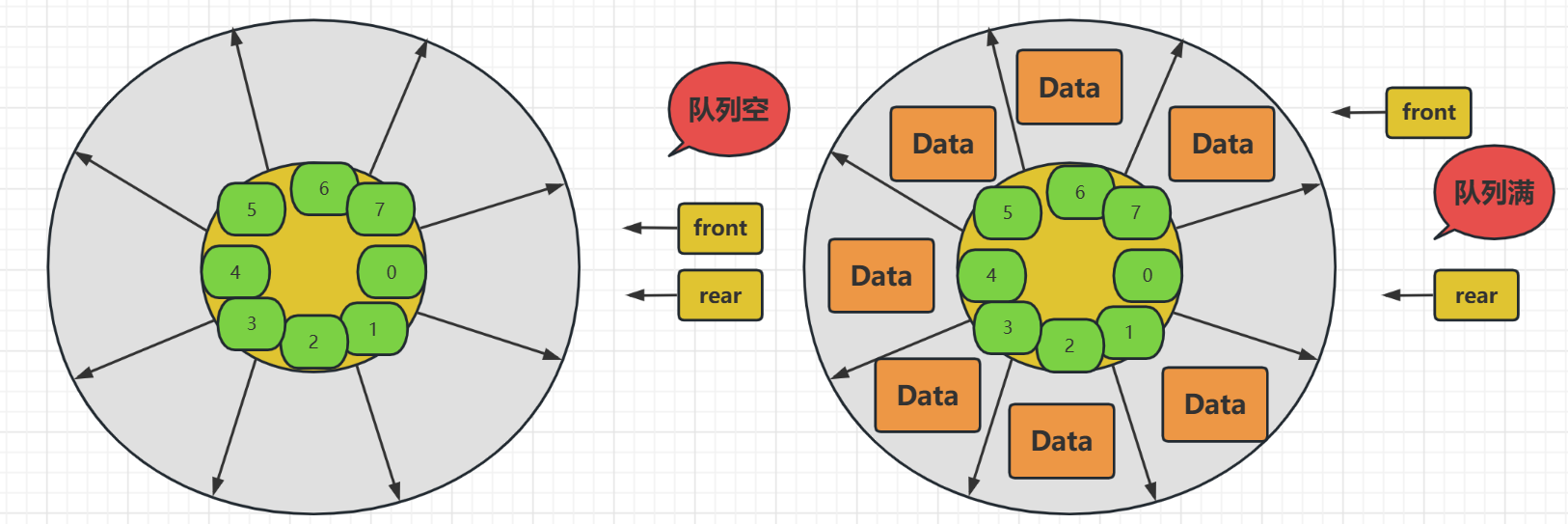
迴圈佇列的設計就很合理,提高了陣列空間的複用性,原本出隊後就不能使用的空間這下也被利用起來了,只是我們在使用迴圈佇列的時候要注意幾個點
- 佇列的下標不能只是當前下標直接加一了當為7的時候應該為0才能迴圈入佇列,所以需要使用當前位置 + 1 取餘 Maxsize
- 判斷佇列為空,初始的時候為空,即兩個指標位置相同時為空,在是順序表中的兩個指標都指向 -1 才為空
- 如果為空是兩指標位置相等那麼,佇列滿還能使用兩指標位置相等嗎?和顯然不能,因為真的兩指標位置相等時不確定佇列滿還是空,所以我們使用front + 1 == rear來判定佇列滿,也就是說,其實我們是有一個空間未使用的,但也是必須的,這樣解決方式是最高效的
下面入佇列的虛擬碼實現
void InQueue(Queue Q,ElementType d){ if((Q->rear+1)%Maxsize == Q->front){ printf("佇列滿!"); return; } Q->rear=(Q->rear+1)%Maxsize; Q->Data[Q->rear]=d; }
下面是出佇列的程式碼實現
ElementType OutQueue(Queue Q){ if(Q->front == Q->rear){ printf("佇列空!"); return ERROR; } Q->front=(Q->front+1)%Maxsize; return Q->Data[Q->front]; // 直接返回,不需要清空剛剛的空間,會被移動覆蓋 // 插入的條件不是當前單元有沒有資料而是 front 是否等於 rear+1 }
大家可以思考,為什在出佇列的時候直接返回就行了,而不用對此空間進行歸零或者打上可插入的標記?
二.連結串列實現佇列
佇列的連結串列實現也可以使用一個單連結串列實現,插入和刪除在兩頭進行,那麼那一頭來做隊頭,那部分做隊尾呢?
連結串列的頭部,肯定是做刪除和新增操作都是沒問題的,主要是是看連結串列尾部
對於連結串列尾部,它新增一個結點沒有問題,直接指標指向那個結點就好了,但是做不了刪除操作,
因為我們的實現方式是單連結串列,它是沒有回頭指標的,一旦尾部來執行刪除操作,一定會使得我們找不到後面的元素,所以連結串列頭部來做刪除,連結串列尾部來做插入
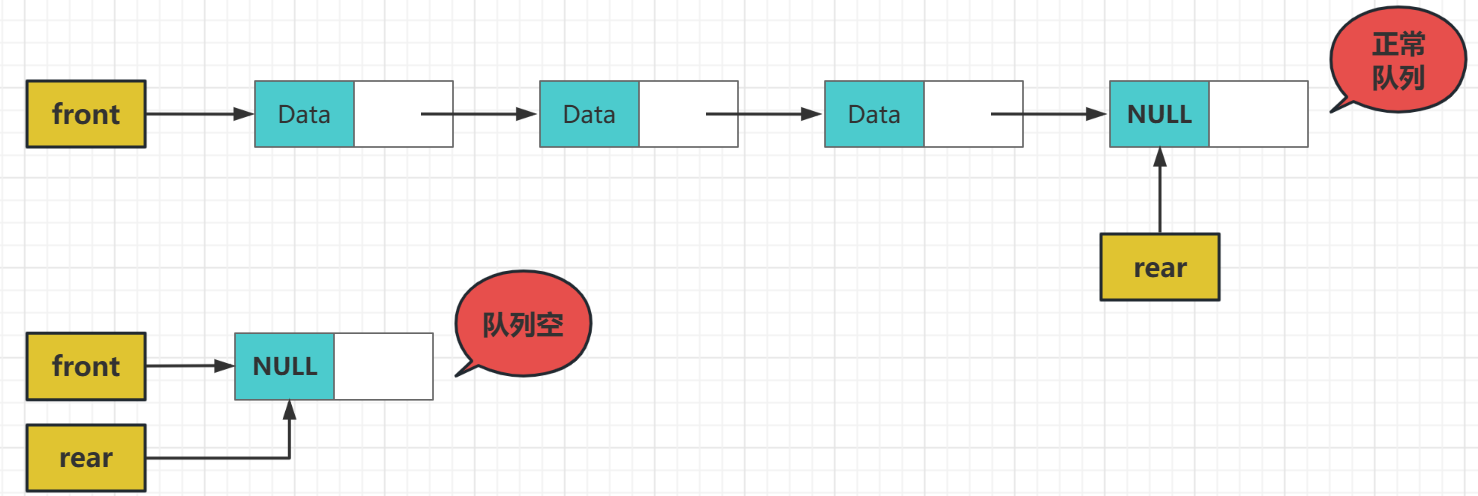
使用連結串列是沒有滿的情況的,除非記憶體被申請滿了,不然就可以一直申請結點來裝新的資料
使用連結串列還是那幾個注意點:
- 刪除結點的時候一定要釋放空間,避免記憶體漏失
- 新增結點通過動態開闢,然後隊尾指標去指向
- 隊空的條件front即隊頭指標指向了null
連結串列的結構體構造要比順序表多一些,它有兩個結構體,一個是資料域,一個佇列的指標域

如上圖,Node結點是用來標識資料域的,而QNode是用來標識佇列指標域的
入佇列結點:
Queue InitQueue() //連結串列都需要初始化一個頭結點 { Queue q; q = (Queue*)malloc(sizeof(Queue)); q->front = q->rear = NULL; return q; } void addQ(Queue Q,ElementType d){ struct Node *temp; temp=(struct Node *)malloc(sizeof(struct Node)); if(temp == NULL){ printf("未申請成功!"); return; } temp->Next=NULL; //下個結點為NULL temp->Date=d; if(Q->rear == NULL) // 新構建的結點是沒有資料的,所以隊頭隊尾都需要新增結點 { Q->front = temp; Q->rear = temp; } else{ Q->rear->Next = temp;//讓n成為當前的尾部節點下一節點 Q->rear= temp;//尾部指標指向新結點 } }
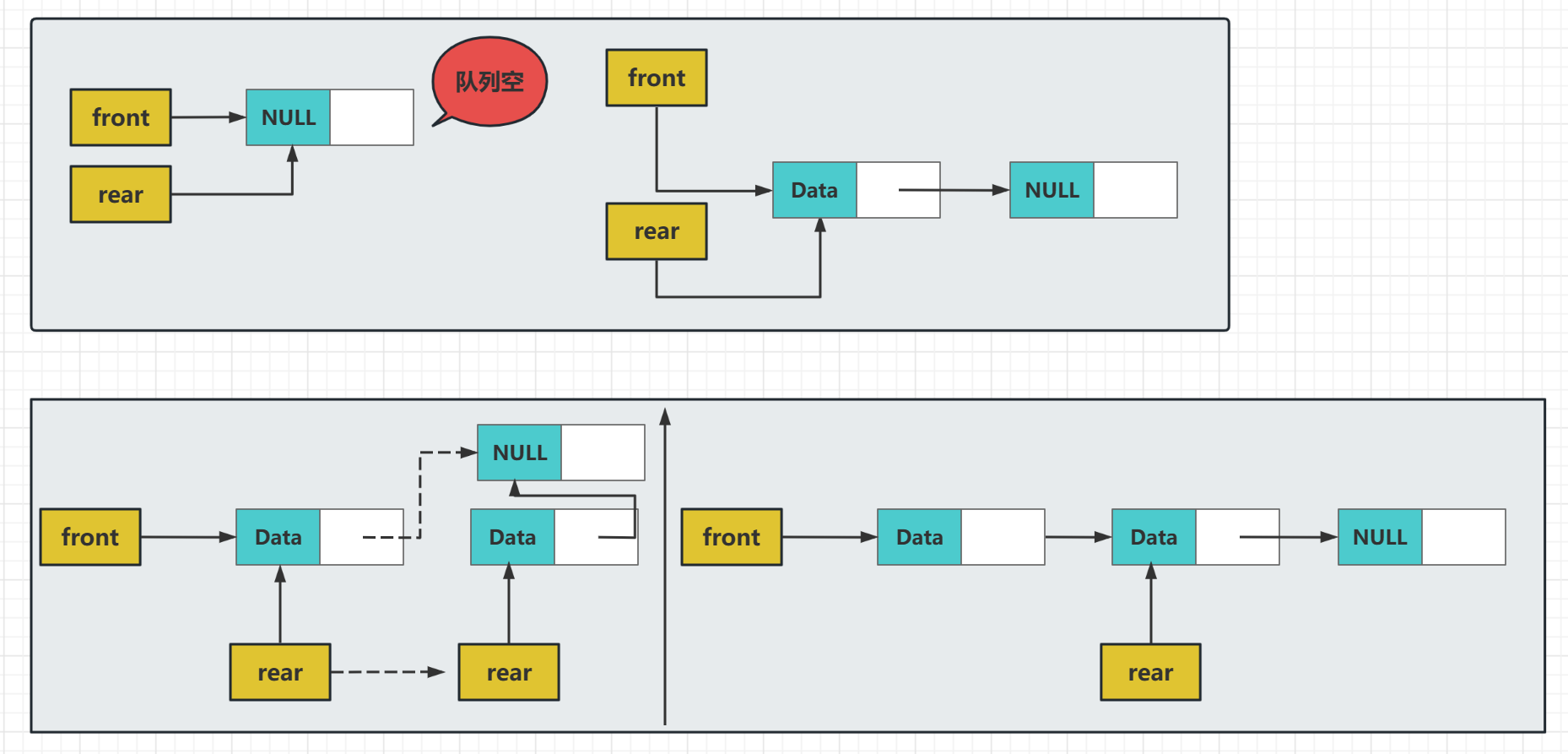
這裡說一下入佇列的幾個注意點:
第一,佇列為空的時候,它們兩個指標都要指向新結點,這裡可以直接指向結點不用其他操作,只是很多人會忘了頭結點也要指向新結點,原因是頭結點也要根據這個新結點來找到下一個結點,所以要注意
第二,然後是佇列裡有資料的情況,雖然不用再關注隊頭指標了,但是這個時候要注意隊尾指標,
它是有兩步操作的,它先需要把整個連結串列鏈起來,也就是當前的最後一個元素的下一個元素要是新增的結點,即 Q->rear->Next = temp;
然後就是把尾部的佇列指標移動到新的結點上去,因為此時它才是尾部結點,即Q->rear= temp;
一步是關聯兩個結點,一步時操作佇列指標,缺一不可
出佇列結點:
ElementType deleteQ(Queue Q){ struct Node *temp; ElementType d; if(Q->front == NULL){ printf("佇列空!"); return ERROR; } temp=Q->front; if(Q->front==Q->rear){ Q->front=Q->rear=NULL; }else{ Q->front=Q->front->Next; } d=temp->Date; free(temp); return d; }
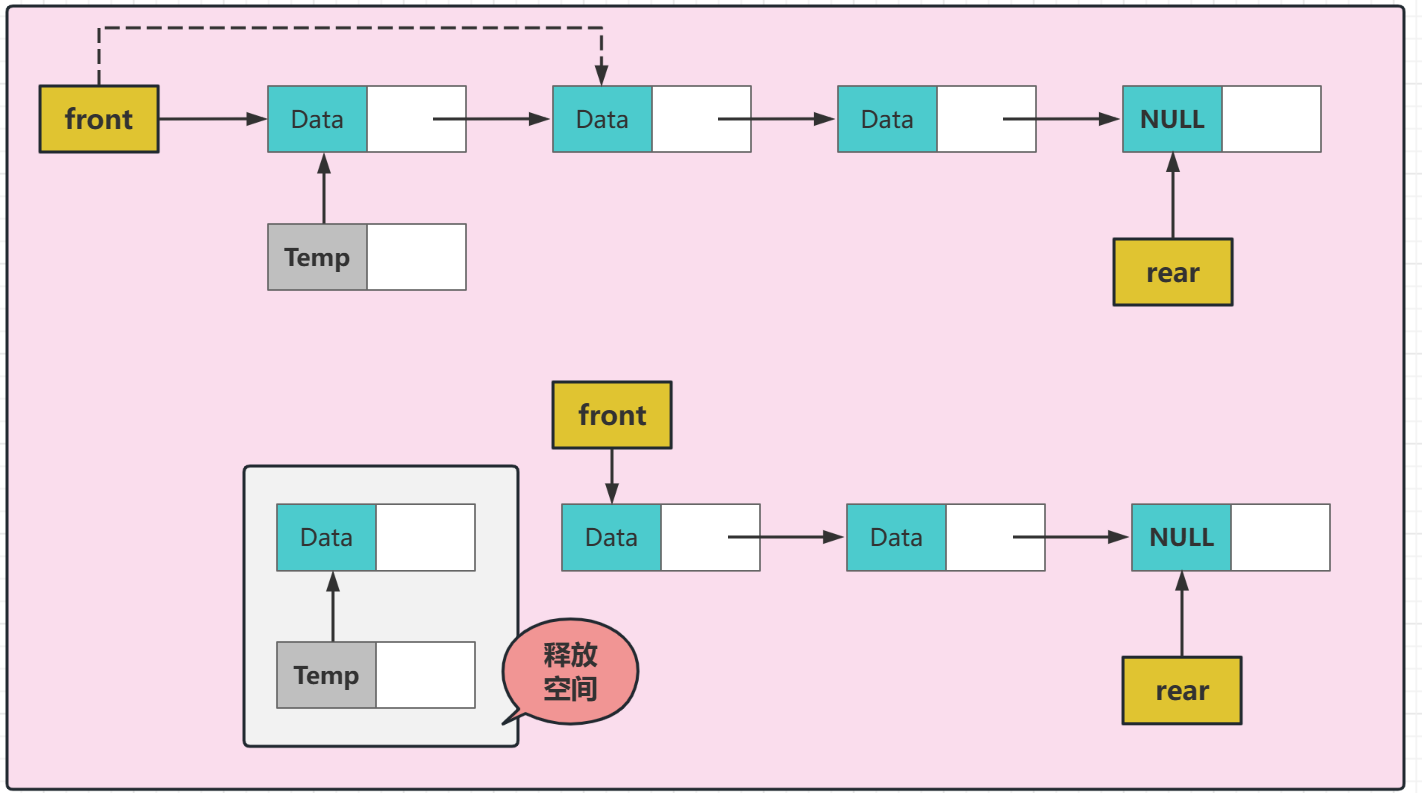
出佇列需要注意的就是:
我們要先用一個指標誌昂我們要出佇列的結點,然後再移動隊頭指標,指向下一個結點
完成指標移動後,需要把剛剛的結點空間釋放掉,如果有返回值就先存放在變數裡面,然後釋放此結點
三.一元多項式的加法
一元多項式相加的規則(預設從大到小儲存一元多項式):
當係數相等的時候:
需要對兩個多項式相加,然後返回
係數不相等的時候:
返回大的多項式

這就是我們設計的多項式結構體,它包含了指數,係數,還有指向下一個多項式的指標
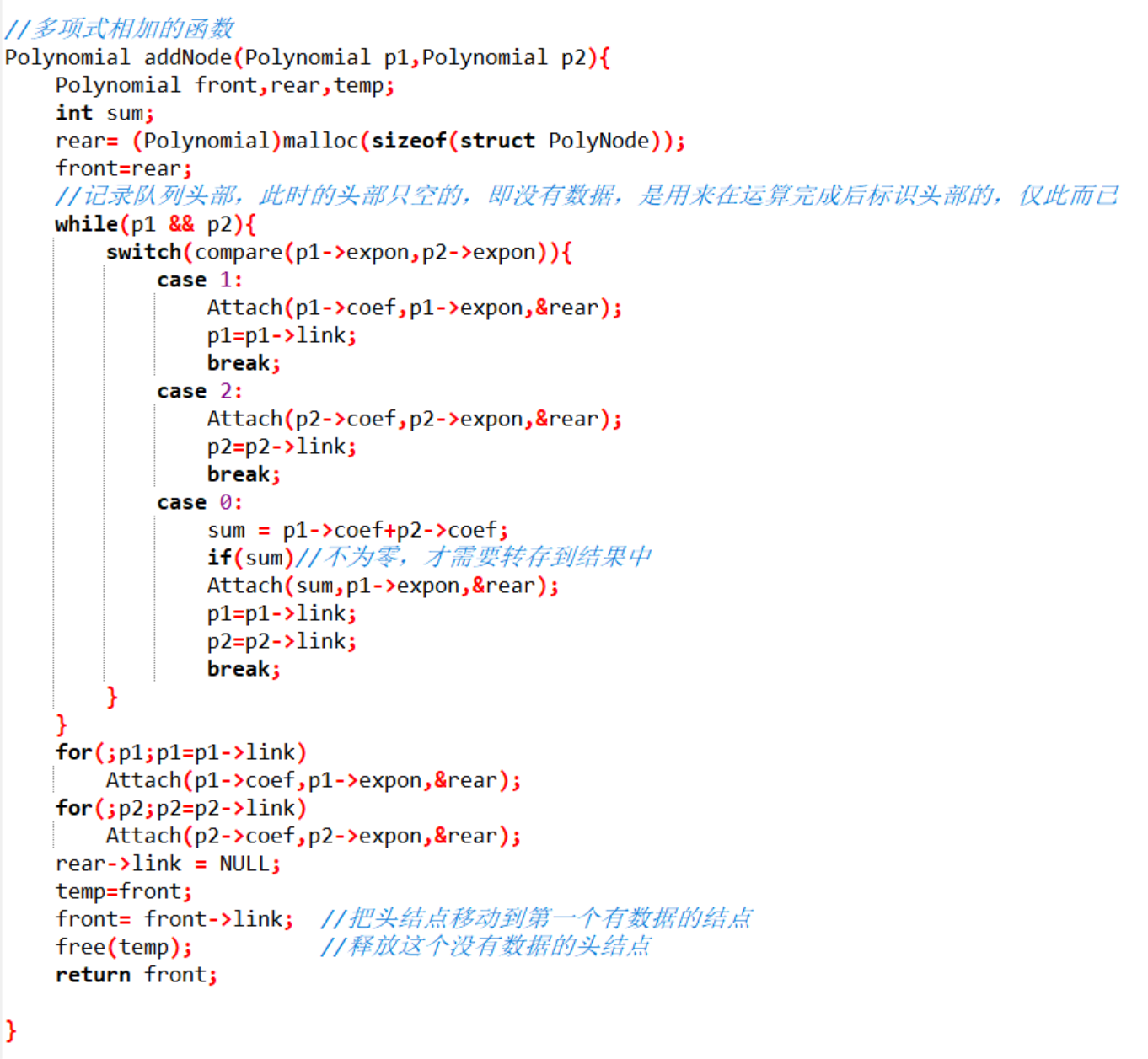
上面的程式碼就是我們計算多項式相加的程式碼,這裡有幾個注意點:
我們為什麼要申請一個頭結點,因為佇列有兩個指標,一個是頭指標標識佇列頭部,一個是尾指標標識佇列尾部,這裡的多項式相加其實是一直入佇列的過程,所以尾指標就一直移動,我們剛開始佇列的兩個指標是在同一位置上的,但是,一旦資料開始入佇列,我們的尾指標就一直在向後移動,而我們的頭指標又要指向資料,所以一共有兩種方式來解決頭指標不移動,且指向第一個元素的問題
第一,初始化兩個指標,讓它們都等於NULL,然後每次新增結點時判斷頭指標是否為空,如果為空,說明頭指標還沒指向第一個資料結點,這下可以指向它,然後下次指向新增結點的時候,就不再動頭結點,而尾指標肯定是一直在移動的
第二,新增一個結點,初始頭尾指標都指向它,然後再計算的時候就不帶頭指標了,新增結點本來都是尾指標的工作,所以可以少很多判斷
我們使用的是第二種方式,這也是為什麼最後我們要釋放當前頭結點的原因,因為這個結點是沒有資料的,是空結點,我們返回值要從有資料的結點開始,所以頭指標要後移一個結點,然後釋放當前結點

這是我們用來回圈構造一元多項式的函數
和連結串列入隊沒有什麼太大的區別都是通過不斷地產生新的結點,然後新增到連結串列的尾部,從而構成一個鏈佇列
最後的完整程式碼展示:
#include<stdio.h> struct PolyNode{ int coef; //係數 int expon; //指數 struct PolyNode *link; //指向下一個結點的指標 }; typedef struct PolyNode *Polynomial; Polynomial p1,p2; // 兩個待相加的多項式 int compare(int a,int b){ if(a>b) return 1; else if(a<b) return -1; else return 0; } //多項式相加的函數 Polynomial addNode(Polynomial p1,Polynomial p2){ Polynomial front,rear,temp; int sum; rear= (Polynomial)malloc(sizeof(struct PolyNode)); front=rear; //記錄佇列頭部,此時的頭部只空的,即沒有資料,是用來在運算完成後標識頭部的,僅此而已 while(p1 && p2){ switch(compare(p1->expon,p2->expon)){ case 1: Attach(p1->coef,p1->expon,&rear); p1=p1->link; break; case -1: Attach(p2->coef,p2->expon,&rear); p2=p2->link; break; case 0: sum = p1->coef+p2->coef; if(sum)//不為零,才需要轉存到結果中 Attach(sum,p1->expon,&rear); p1=p1->link; p2=p2->link; break; } } for(;p1;p1=p1->link) Attach(p1->coef,p1->expon,&rear); for(;p2;p2=p2->link) Attach(p2->coef,p2->expon,&rear); rear->link = NULL; temp=front; front= front->link; //把頭結點移動到第一個有資料的結點 free(temp); //釋放這個沒有資料的頭結點 return front; } // 資料生成佇列連結串列的函數 void Attach(int c,int e,Polynomial *pr){ Polynomial p; p=(Polynomial)malloc(sizeof(struct PolyNode)); p->coef=c; p->expon=e; p->link=NULL; (*pr)->link=p; *pr=p; } // 實際讀入的一元多項式的函數 Polynomial ReadPoly(){ Polynomial p,rear,t; int c,e,n; printf("請輸入,一元多項式的個數!\n"); scanf("%d",&n); p=(Polynomial)malloc(sizeof(struct PolyNode)); if(p==NULL){ printf("error\n"); return; } p->link=NULL; rear=p; printf("請從指數大到小輸入多項式:\n"); printf("模板:係數 指數\n"); while(n--){ scanf("%d %d",&c,&e); Attach(c,e,&rear); } t=p; p=p->link; free(t); return p; } // 一元多項式的輸出函數 void PrintPoly(Polynomial p){ int flag=0; if(!p){ printf("0 0\n"); return; } while(p){ if(!flag) flag=1; else printf("+"); printf("%dx^%d",p->coef,p->expon); p=p->link; } } int main(){ Polynomial p1; Polynomial p2; Polynomial p3; p1=ReadPoly(); p2=ReadPoly(); p3=addNode(p1,p2); PrintPoly(p3); }
補充:二級指標
所謂二級指標,它的作用是存放一級指標的值
我們的普通變數的值可以被一級地址指向
一級指標它也有它自己的地址,它又不是個鬼,它的地址就會被一級地址指向
只不過一級地址在初始情況下,沒有指向變數的時候它的地址是一個不可存取的空間,但是它自己還是有屬於自己的地址,只是指向的地址是不可存取的初始化地址
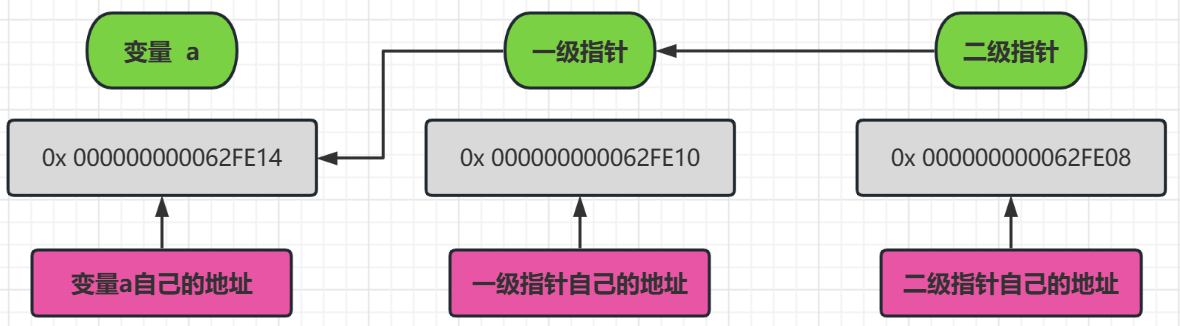
我們可以看到,指標的內部都是地址,但是操作起來可能就不一樣了
也就是當 * 號操作符操作到一級指標的時候,取得的是變數 a 的值,一個具體的型別變數
當一個 * 號操作符操作到二級指標的時候,取得的是變數 一級指標的地址,也就是 a 的地址
當兩個 * 號操作符操作到二級指標的時候,取得的就是 變數 a 的值,一個具體的型別變數
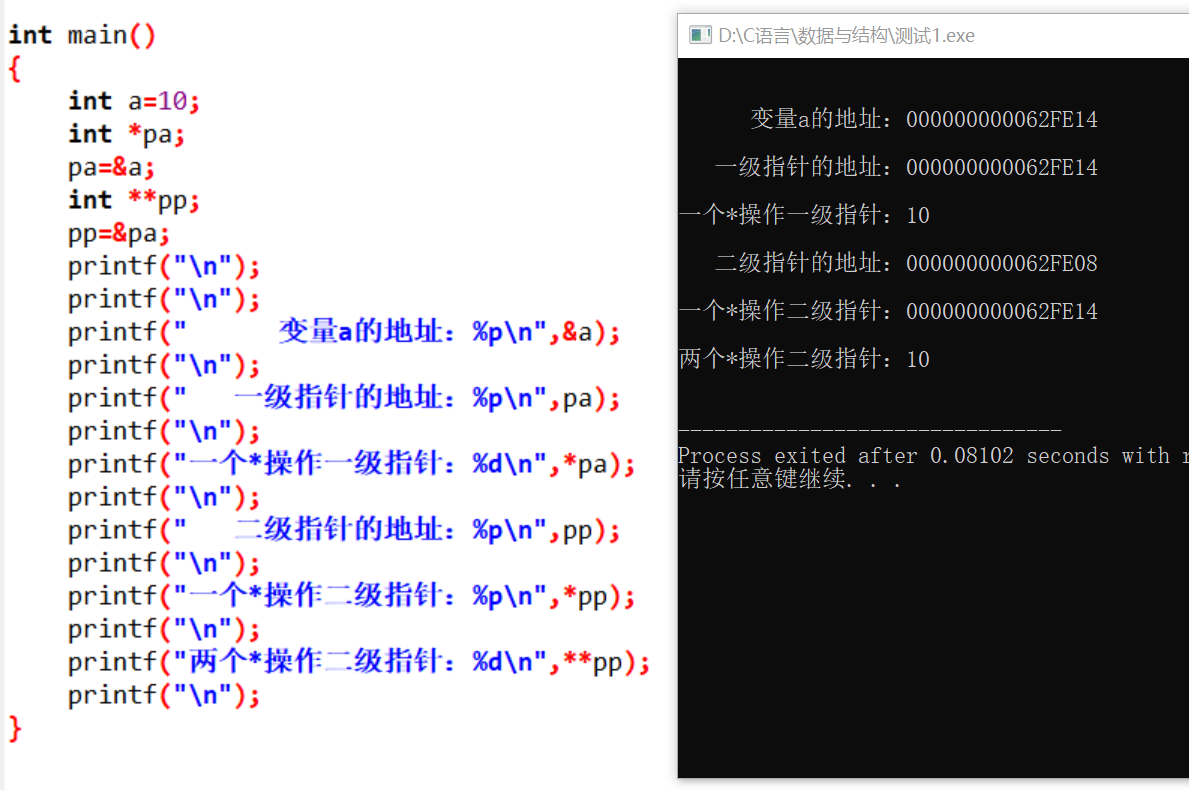
大家也可以自己去敲敲命令看看,通過觀察就可以發現二級地址和一級地址在概念上應該是大差不差的
在函數的引數傳遞的時候,我們就會發現會使用到二級指標,因為那個函數可能要對鏈佇列的最後一個元素操作,你要是直接傳入一個指標進去,它不知道整個鏈佇列的隊尾在哪
所以你可以直接把隊尾的地址傳進去,直接在當前的地址後面新增結點