作者：vivo 網際網路伺服器團隊- Gong Bing

本文將學術界和工業界的糾刪碼技術的核心研究成果進行了相應的梳理，然後針對公司線上儲存系統的糾刪碼進行分析，結合網際網路企業通用的IDC資源、伺服器資源、網路資源、業務特性進行分析對原有糾刪碼技術進行優化和微創新，提出了融合EC整體方案以及可落地的RS+LRC+中間結果優化+並行修復跨AZ頻寬設計方案，為後續的工程實踐提供重要原理和架構支撐。

引言

本文借友商輪值CEO 於2020年8月28日在長沙「數學促進企業創新發展論壇」上分享的《後夏農時代，數學決定未來發展的邊界》【85】進行開篇，發言提出了後夏農時代，ICT資訊工業面向數學的十大挑戰性問題，其中就有一項「高效的糾刪碼問題」，雖然這個問題的提出背景是出於通訊編碼領域，但對於糾刪碼在儲存領域的使用同樣面臨著具大的機遇與挑戰。

圖1：糾刪碼問題挑戰

針對糾刪碼的研究分為兩派：

• 一派則是純理論界針對糾刪碼編碼技術在編解碼複雜度、修復頻寬及磁碟IO、儲存開銷等維度進行研究提出新的理論完備性證明過的糾刪碼，這類研究可能考慮更多的是理論完備性的證明；不會考慮工程界的實現複雜度等情況；

• 一派是不改變編碼理論，利用糾刪碼結合生產環境進行適當改造（多AZ、異構伺服器、大條帶、跨rack等）再結合實驗資料在修復開銷、儲存開銷、可靠性等指標來證明價值。這兩派的研究相輔相成共同推動糾刪碼技術在分散式儲存領域的發展。

本次分享的主題「糾刪碼技術在vivo儲存系統的演進」，分為上下兩篇：

• 上篇側重介紹和分析糾刪碼技術的演進歷程、核心糾刪碼技術的原理和以及工業界儲存產品當中的糾刪碼技術的探索與實踐，最後介紹vivo儲存系統在糾刪碼技術上的一些探索；

• 下篇重點展開介紹儲存團隊在糾刪碼領域的研究成果及糾刪碼研究成果在vivo儲存系統中的實踐，與工業界儲存產品中的糾刪碼相關指標進行全方位對比，以及未來的一些規劃。 

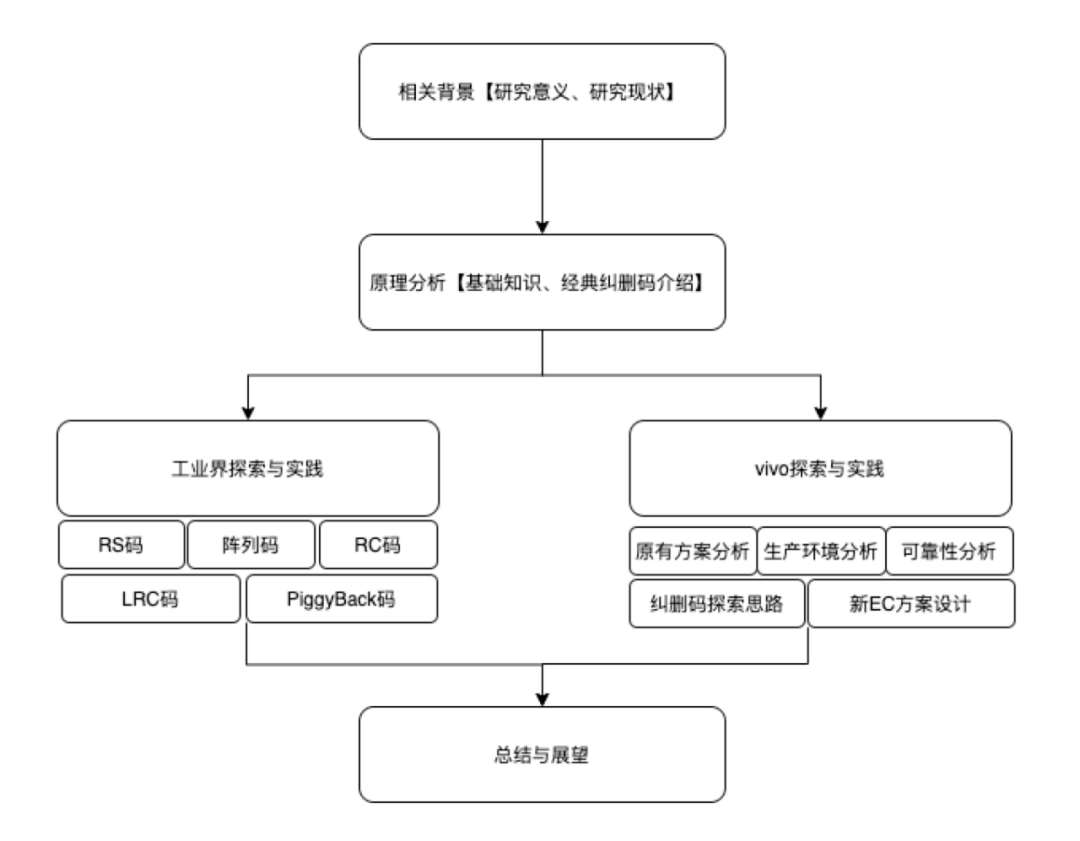
圖2：本文的組織結構

注：本文當中有大量的專業術語，不可能所有術語都去作個解釋，因此針對不懂的有些術語可以自行去搜尋相關含義

一、相關背景

1.1 研究意義

分散式儲存系統為了降低成本往往採用大量廉價通用的伺服器提供服務，然而這些伺服器的磁碟的可靠性是個很大的問題，其平均壽命在2-7年，還受外部環境因素的影響，受限於其機械構造，磁碟會發生磁碟故障、磁區故障和不可檢測磁碟故障等。因此，分散式儲存系統為了提高原始資料的可靠性，副本和糾刪碼是兩種最常見的資料冗餘方法。副本將原始資料複製到n份，並儲存到不同的儲存節點上，能夠容忍任意n-1個節點失效，其缺點是儲存開銷大。糾刪碼則以計算資源換儲存資源，採用了一種更高效的方式增加資料冗餘，因此，糾刪碼成為了當前雲端儲存的主流資料冗餘方式，並且持續成為學術界和工業界在儲存領域的一種研究熱點。

圖3：使用糾刪碼技術公司列表

1.2 研究現狀

糾刪碼也被稱為糾錯碼，它將原始資料編碼為資料量更大的編碼資料，並能夠利用編碼後的部分編碼資料恢復出原始資料。當有節點發生故障時，要恢復這個節點的資料需要讀取多個節點的資料，這個過程會消耗大量的網路頻寬和磁碟IO，另外解碼複雜度對業務可用性和資料可靠性也有影響，解碼複雜度越高，則臨時修復時延就高，從而增加業務讀取時延；因此，影響糾刪碼好壞的指標很多，主要有如下一些指標：以下指標都是以可靠性統一基準的前提下進行參考：

• 【編碼複雜度】編碼複雜度決定了資料寫入的時延

• 【解碼複雜度】解碼複雜度決定了讀取的時延以及節點故障時資料臨時修復及永久修復的時延

• 【修復網路頻寬】節點故障時資料修復所需消耗的整體網路頻寬，這個指標非常關鍵

• 【修復磁碟IO】磁碟IO消耗和網路頻寬一般成正比，考慮大部分儲存伺服器是高密伺服器，一般網路會是瓶頸

• 【修復節點數】修復節點數減少，往往也就降低了修復需要的網路頻寬 

• 【更新複雜度】更新複雜度是指一份資料有少量更新操作，比如更新一兩個位元組很頻繁所涉及的相關操作複雜度

• 【儲存開銷】這個指標是指的編碼效率，編碼效率越高，儲存開銷越低

• 【引數限制】比如糾刪碼的碼長受不受限制等等

以應用最為廣泛的【n,k】RS碼【2】為例，RS的碼長為n，碼的維度為k，當出現有節點故障時，需要k個節點進行恢復，同時可以容忍n-k個節點的故障，這種編碼也被稱為最大距離可分糾刪碼MDS【3】，對應上述指標也就意味著相同的容錯能力下RS碼的儲存開銷小，另外RS碼的碼長不受限制，這也是RS碼如此受歡迎的原因；而在通訊領域大殺四方的LDPC【4】糾錯碼在儲存領域應用較少，原因就是因為LDPC不滿足MDS特性，容錯能力不限，意味著相同的容錯能力LDPC需要更大的儲存開銷, LDPC更多是應用在磁碟內部的冗餘；而得益於早期在RAID5和RAID6中的廣泛使用，具有MDS特性的陣列糾刪碼也被嘗試著應用在分散式儲存系統當中，MDS陣列碼相對於RS碼全是互斥或操作，編解碼相對RS碼複雜度低，但是同時相關引數有所受限，這也抑制了它在分散式儲存的廣泛應用；常見的陣列碼有EVENODD碼【5】、RDP碼【6】、STAR碼【7】支援3容錯、Liberation碼相對EVENODD更新複雜度接近理論下界【8】，ZigZag碼【9】磁碟IO開銷達理論下界，Blaum-Roth碼【10】基於多項式環上構造的MDS陣列碼，相對於RS是編解碼複雜度要低些。

另外針對RS碼高昂的網路修復頻寬，湧現出一類再生碼【11】來降低修復中所要消耗的頻寬。再生碼是一類通過允許節點傳送編碼過的資料來使得修復中可最小化修復頻寬的糾刪碼，其可在不增加儲存開銷的情況下顯著降低修復頻寬。Dimakis等人將再生碼分為兩大類：MSR碼【23-47】和MBR碼【12,13】。MBR碼是最小化修復頻寬主要分為Polygonal MBR Code【14】和Product-Matrix MBR Code【15】；MSR碼是在最小化儲存開銷下降低修復頻寬，又分為精確修復碼和功能修復碼，精確修復碼是指通過修復可修復出原始丟失資料，功能修復碼則不保證，資料讀取每次都需要進行解碼操作。比如Hu等人提出了一種功能性MSR碼F-MSR【16】，精確性MSR研究主要基於Product-Matrix MSR【26】，還有比如Butterfly碼【48】、Coupled Layer Code碼【38-40】等當前已經在工業界有所應用的再生碼。最近又有一些工作【18,19,20】是針對跨機架頻寬和機架內頻寬進行區分，為最小化跨機架頻寬為目標減少修復頻寬。降低修復頻寬還有一些其它的研究工作，比如2013年Rashmi等人提出Piggybacking框架【22】，框架以MDS碼為基本碼通過將子條帶資料嵌入其它條帶來顯著降低修復頻寬，Piggybacking框架的編碼設計也有很多研究成果。【79-81】

針對修復節點數降低這個指標，Huang等人提出了一種區域性修復碼LRC【17,21】通過對傳統編碼資料塊進行分組，並針對每組生成校驗塊，從而使得單塊修復只需要組內節點參與修復提高修復效能。但由於引入額外儲存開銷，LRC沒達到儲存最優。但由於LRC的簡易性，工業界有很多的實踐反饋，因此LRC逐漸成為近年來糾刪碼領域的研究熱點【66-78】。LRC的一個分支MRC碼的研究PMDS也吸引了不少關注【49-60】，除了單節點修復相關的LRC碼的構造，針對修復多個節點的LRC碼【62-65)】是一個研究方向，另外，結合LRC和RC的Local Regeration Code【61】也是個研究思路。

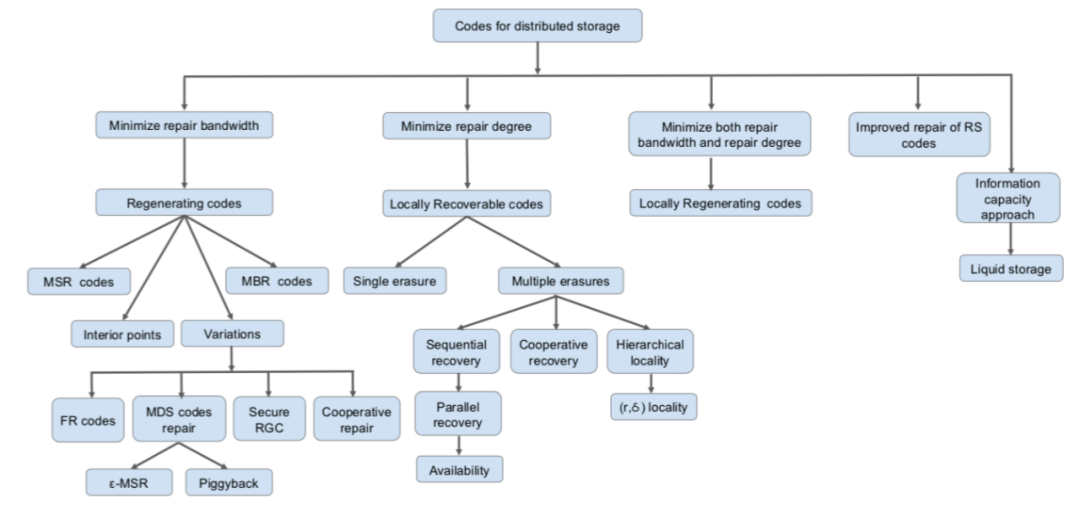
圖4：糾刪碼研究方向概覽

二、原理解析

2.1 基礎知識介紹

概念1：糾刪碼原理

糾刪碼通用由兩個引數n和k來進行設定，稱為(n,k)編碼。在分散式系統當中，通常將資料以固定大小的塊進行組織，編碼時，儲存系統將k個資料塊進行編碼生成額外的n-k = m個大小相同的校驗塊，這樣n個資料塊和校驗塊中有任意的磁碟節點故障，都可以通過其它的磁碟節點進行解碼恢復丟失的資料。以下為糾刪碼的一個示意圖：

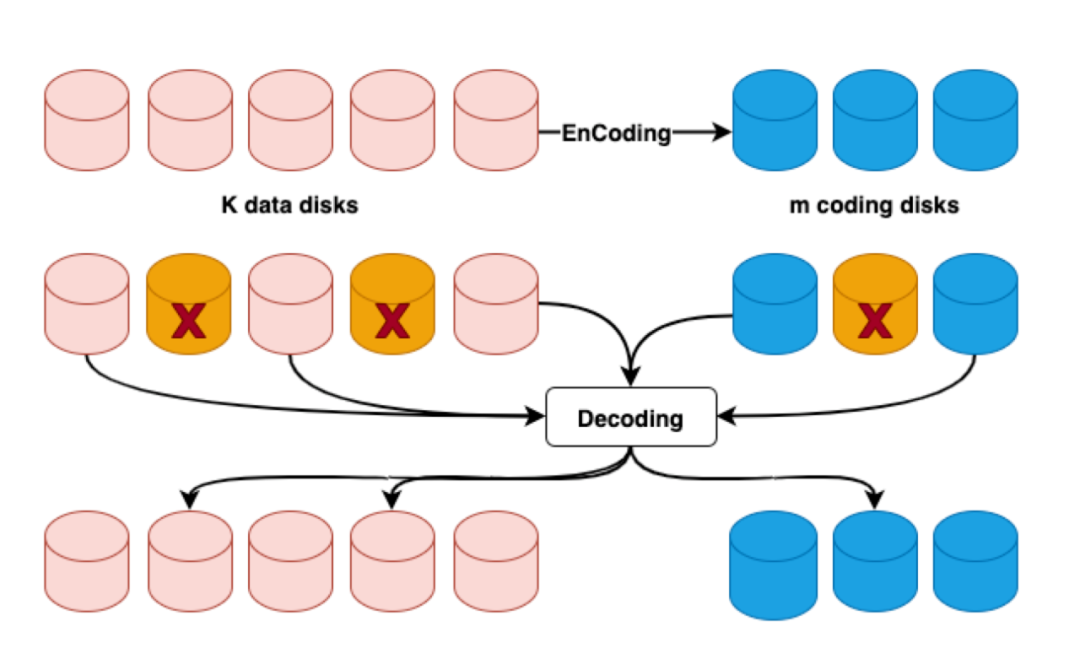
圖5：糾刪碼原理示意圖

概念2：Singleton頓界

假設C是一個引數為[n,k]的線性碼，則C的極小距離d≤n-k+1。以上表明一個線性碼的極小距離不會「太大」，無論怎樣努力，都不能夠構造出一個引數為[n,k]的線性碼，使得它的極小距離大於n-k+1，這個n-k+1就稱為Singleton界。

概念3：MDS特性

一個引數為[n,k]的線性碼C，若滿足dmin(C)=n-k+1，則稱該碼為極大距離可分碼，簡稱為MDS（Maximum Distance Separable）碼。

概念4：系統性

系統性就是系統中儲存了k個資料塊可用來直接存取，如果故障的節點沒包括資料塊，則不影響資料的讀取，系統性可降低讀取時延。非系統性則在每次讀取時都需要進行解碼操作，讀取時延相對偏大。

2.2 經典糾刪碼介紹

2.2.1 Reed-Solomon Code

RS碼最早是ECC領域的一種糾錯演演算法，RS編碼演演算法是一種典型的系統編碼，也是一種典型的MDS性質的編碼。

RS碼基本思想其實就是拉格朗日插值多項式，我覺得用拉格朗日插值多項式來推導RS碼相對於其它文獻的講解會更清晰，下面我們簡單回顧一下拉格朗日插值多項式：對於任何k階的多項式函數f(x)=a0+a1x+a2x^2+...+akx^k，我們很容易通過任意的n+1個點(x0, f(x0)，(x1,f(x1))，... (xk,f(xk))對這個多項式進行恢復。

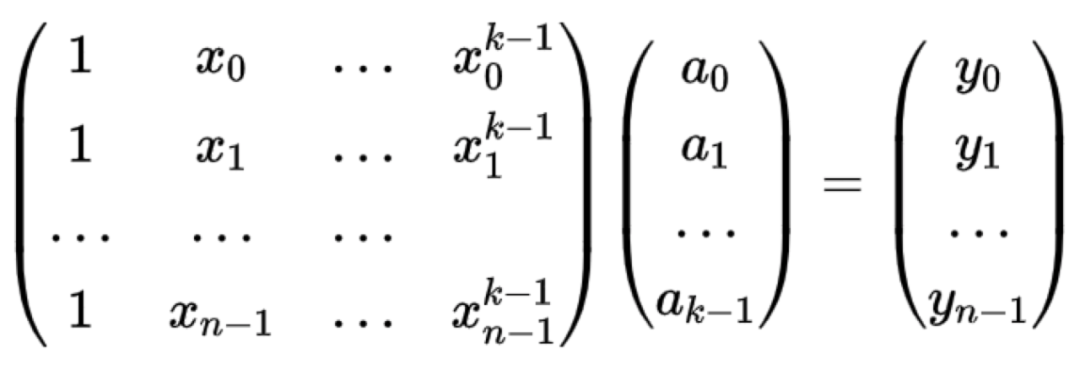
解碼過程如下：

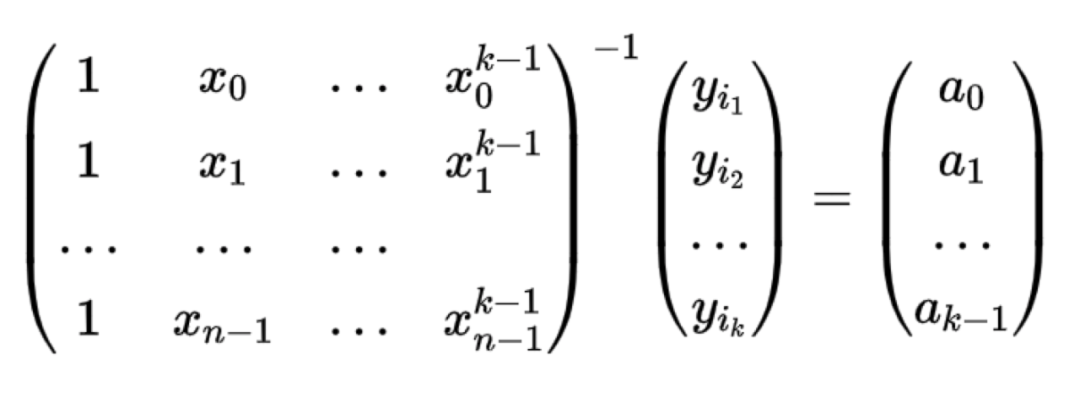
那麼RS碼是如何使用拉格朗日插值的呢？對於一個(n,k)的RS碼，假設a0,a1,...ak-1在Fq域內的k個傳送訊號，我們在Fq中取樣n個插值點x0,x1,...xn-1，則可以得到拉格朗日插值多項式為：

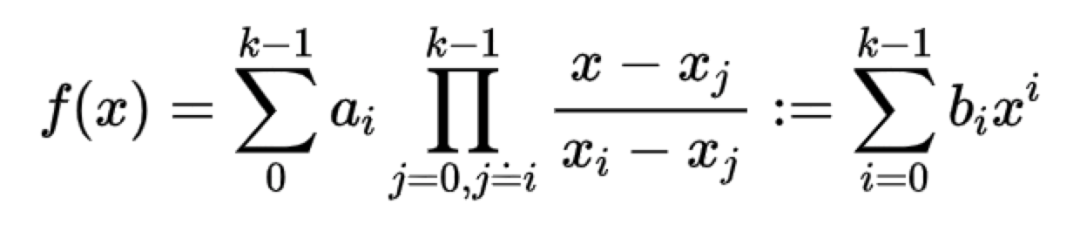
不難發現，前k個插值的多項式值有如下：

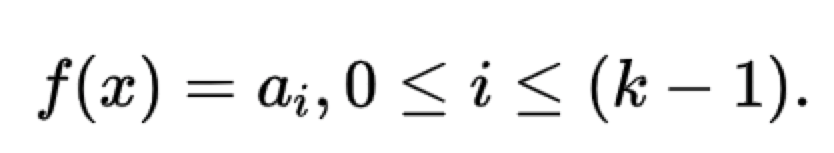
如果用矩陣來表示則為：

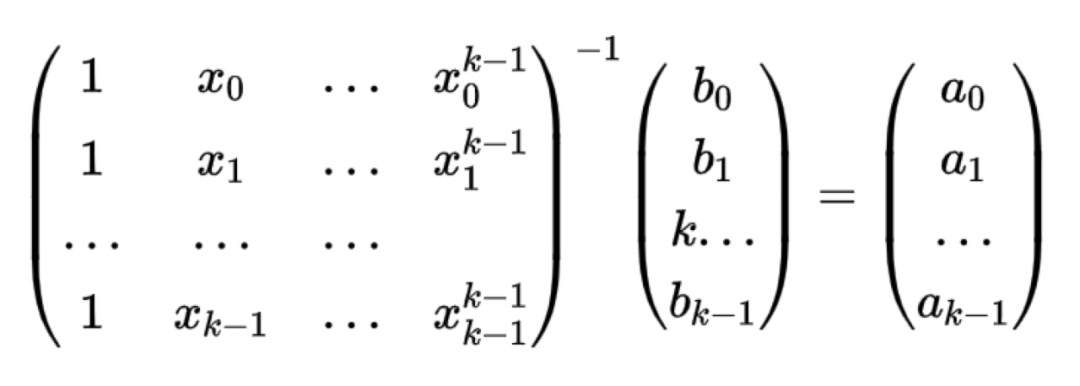
令上式的範德蒙德矩陣的逆*a向量 = b向量，則校驗矩陣有如下：

【A|B】【A^-1】 a向量= 【E|BA^-1】* a向量 = 【a0,a1,...ak, c1,...cn-k】

這樣就有了經典的(A Performance Evaluation and Examination of Open-Source Erasure Coding Libraries For Storage)描述Reed-Solomon碼的編解碼方式如下圖所示：

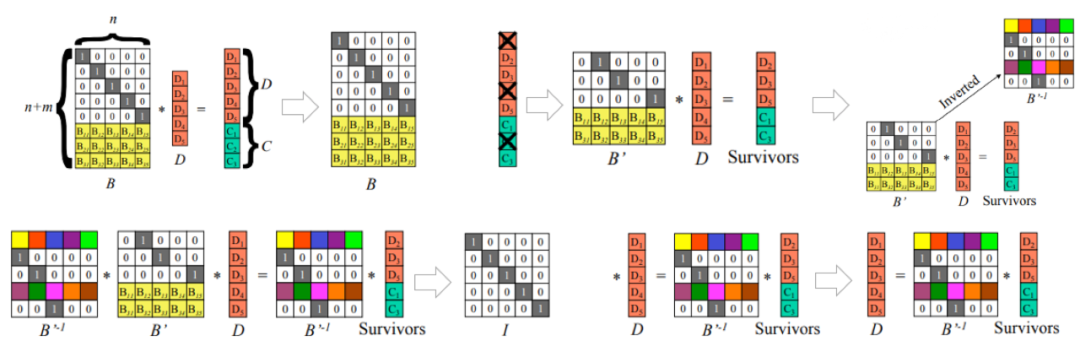
圖6：RS編解碼示意圖

可以看出，RS(n,k)碼一個滿足MDS性質的編碼，當有資料丟失需要k個節點同時進行恢復，另外，允許n-k+1個節點同時資料丟失。

2.2.2 MDS Array Code

MDS陣列碼是一類比較特殊的線性分組碼。陣列碼相對於RS碼避免了有限域計算，僅通過互斥或運算實現糾刪碼。在這類碼中，符號均為m維的列向量，從而每個碼字都是一個m*n的二維陣列。絕大部分的陣列碼都是二元陣列碼，陣列碼的每一列可以全是資料位也可以既有資料位也有校驗位。以下為一個m=2, n = 5, k = 3的陣列碼的示意圖：

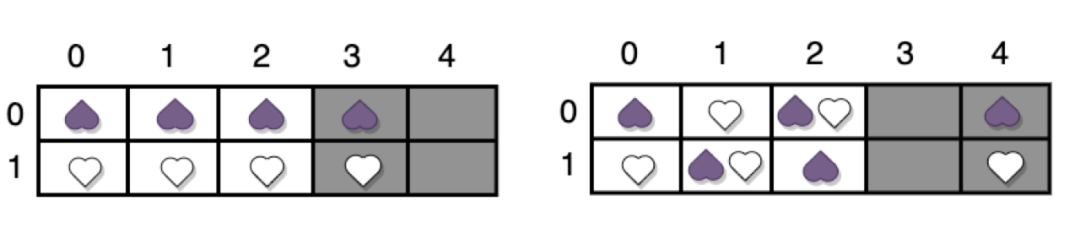
圖7：陳列碼示意圖

不難看出該碼的奇偶校驗方程為：

 

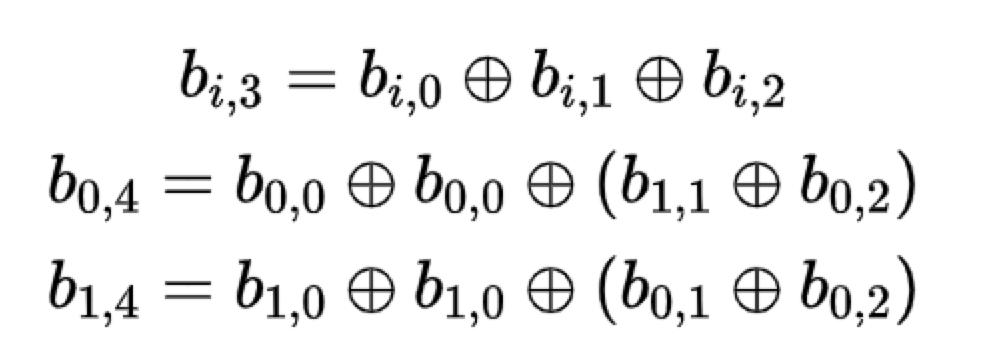
（1）EVENODD Code

EVENODD碼是一種允許丟雙列的容錯碼，有兩列的校驗列，是繼RS碼後最先運用在RAID當中的碼，它是一個(m-1)*(m+2)的陣列碼，其中m是一個素數。第m+1列和第m+2列的編碼方式如下： 

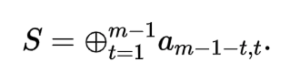
另外，對於每一個l，0<= l <= m-2，可以通過以下方式獲取冗餘符號：

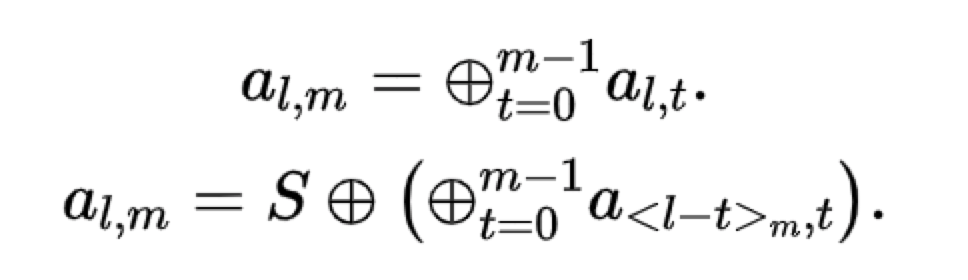
可以看到，第m+1列校驗碼的構造是前m列的資料位的互斥或；第m+2列的校驗碼的構造則是通過追加沿斜率為1的對角線互斥或和來達到容錯目的。EVENODD碼推出後，針對斜率不為1引入到糾刪碼的研究作為EVENODD碼的推廣為也就不足為奇。

圖8：EVENODD碼示意圖

（2）RDP Code

RDP碼的碼字結構與EVENODD碼非常類似，只是比EVENODD碼少了一個資料列，是一個(m-1)*(m+1)陣列碼，其中m是一個素數。RDP相對於EVENODD編解碼複雜度都要低不少，因此在RAID應用廣泛。

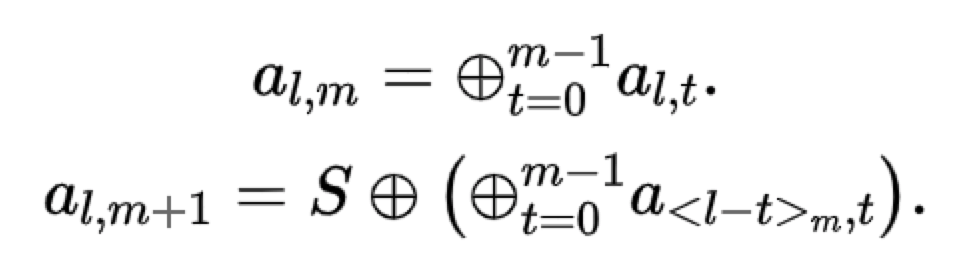
RDP碼的編碼結構示意框圖如下所示：

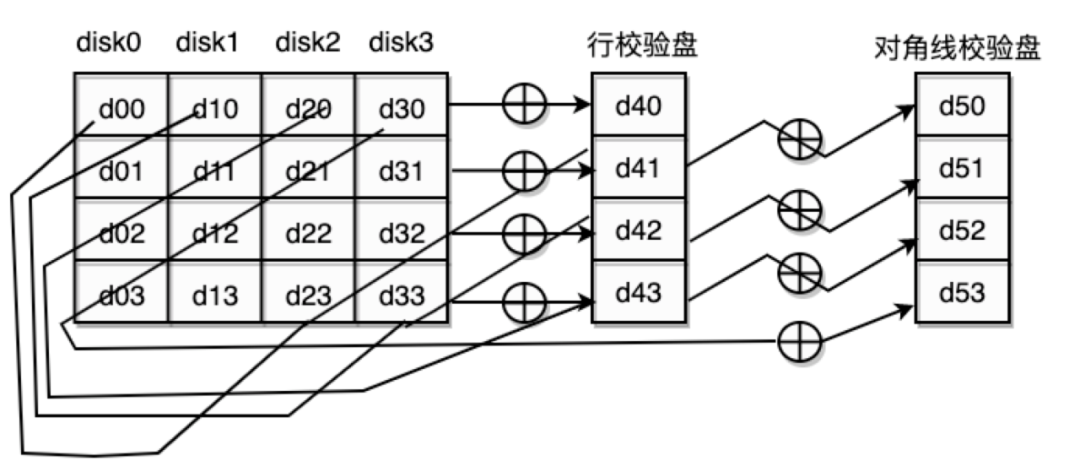
圖9：RDP碼示意圖

2.2.3 Regeration Code

在討論再生碼這前我們來分析一下儲存開銷和修復開銷的關係，從定性分析，我們很容易理解，當位元速率越大，儲存空間效率越高，修復所需要的資料量就越大。A.G.Dimakis等人首次利用資訊流圖推匯出儲存開銷與修復開銷滿足以下：

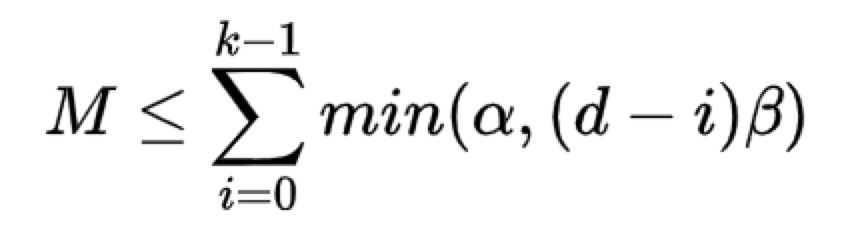
其中，alpha代表每個節點儲存資料量，belta代表修復過程中每個參與節點傳輸的資料量，d代表輔助節點的個數。那麼儲存開銷為所有節點儲存量的總和。n* alpha。而修復開銷是所有參與修復的儲存節點所需要傳輸的資料量，d* belta。不難看出，alpha和belta不可能同時最小，alpha最小也就是M/k；belta最小也就是上式所有的(d-i)* belta都最小，可以求得d * belta = 2Md/(2kd-k^2+k)。

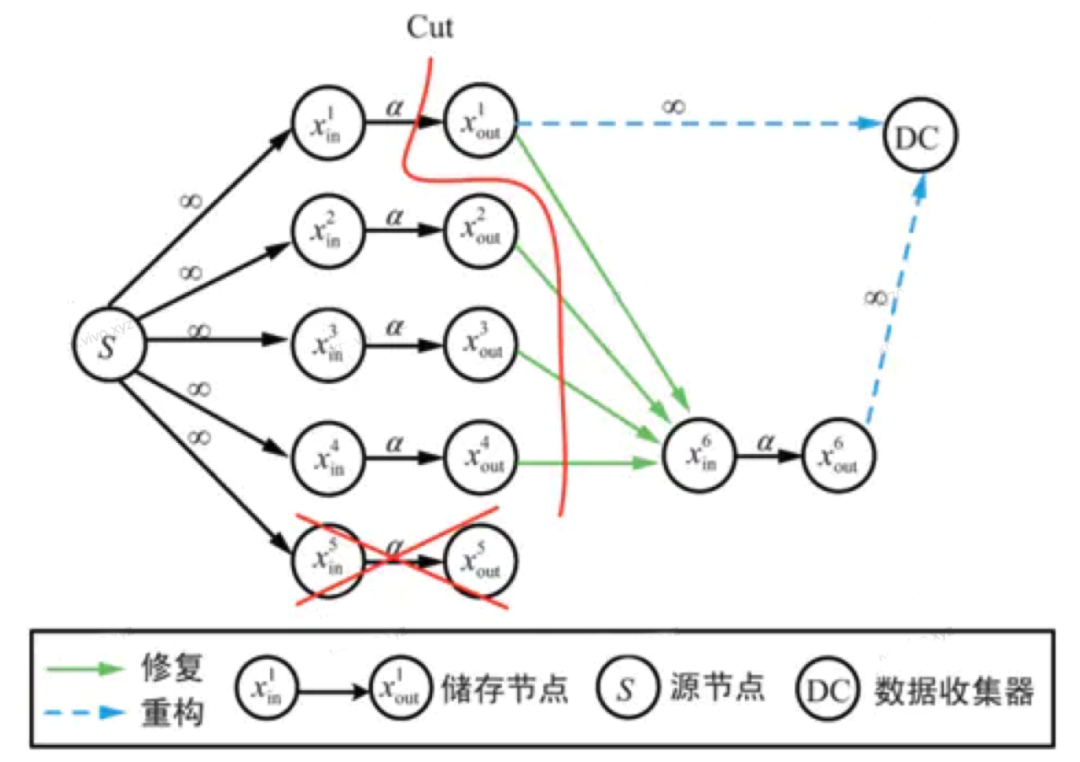
圖10：再生碼資訊流圖

（1）MSR

MSR全稱為最小儲存再生碼Minimum Storage Regenerating碼，不難理解，MSR是保證了儲存消耗最小，所以MSR的儲存資料塊大小和失效修復頻寬值計算公式如下：

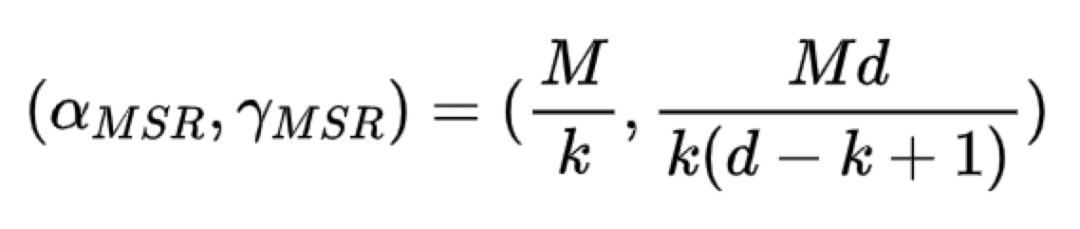
具體的編碼方式就不介紹了，在下一章節介紹的Clay碼就是MSR的一種工業上的應用MSR碼。通過公式不難看出，d越大，修復開銷越小。MSR的研究方向學術界和工程界側重點有所有同，學術界是不考慮分包數大小，為了不斷逼近最小的修復頻寬去儘可能設計MSR碼或者固定分包數然後在固定分包數下不斷的去降低修復頻寬；而工程界則更多考慮設計出分包數不高但是修復頻寬低的MSR碼，因為需要考慮工程實現。

（2）MBR

MBR全稱為最小頻寬再生碼Minimum Bandwidth Regenerating，不難理解，MBR是保證了單節點失效修復頻寬最小，所以MBR的儲存資料塊大小和失效修復頻寬值計算公式如下：

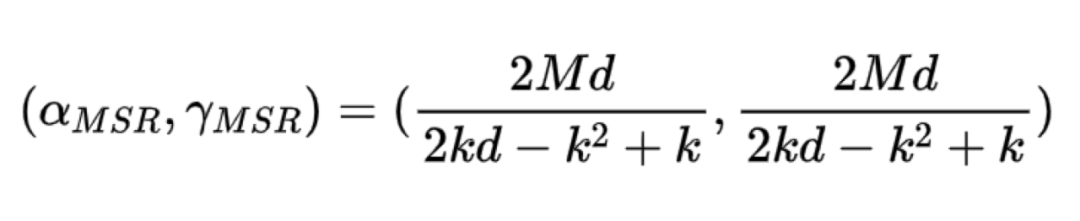
MBR相對於MSR實用性沒有那麼高，原因是因為分散式系統更多的是在儲存開銷最小化的情況去儘量降低修復頻寬，因而MBR的研究熱度沒有MSR那麼高。

2.2.4 Locally Repairable Code

區域性修復碼則是通過一類增加額外的儲存來將資料修復儘可能在少量節點內完成，從而達到大大降低網路開銷操作的糾刪碼。由於引入了額外的儲存開銷，區域性修復碼並沒有達到儲存最優。但是區域性修復碼實現簡單，因此生產環境有了很多的實踐，當前，LRC編碼成為最近幾年糾刪碼研究領域的一個熱點研究方向。

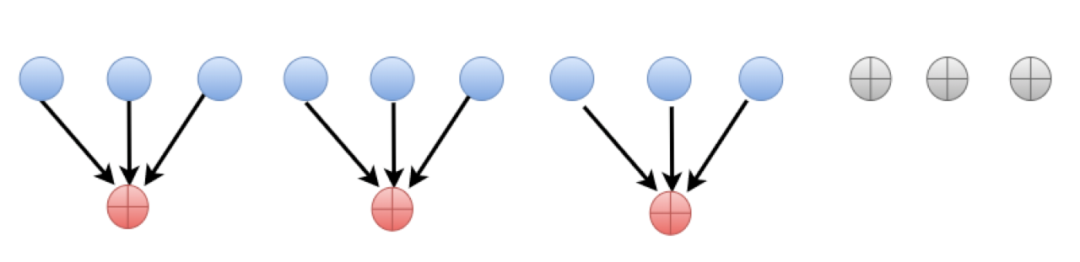
圖11：LRC碼示意圖

Singleton-型上界：

針對於一個(n,k,r)的區域性修復碼，即碼長為n的碼中有k個資訊位和具有區域性修復性r，則有一個經過證明的該碼的最小距離d(C)滿足上界如下：

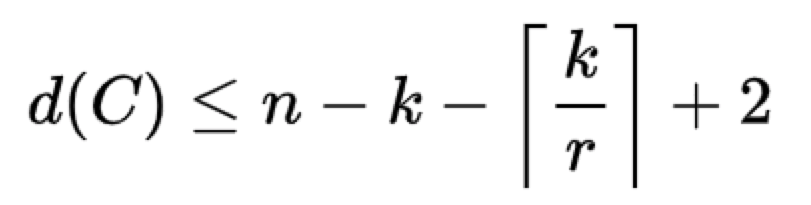
任何一個達到這個界的區域性修復碼稱為最優區域性修復碼。因此，設計達到最優區域性修復的碼是LRC方向的一個研究熱點。

上述區域性修復碼只能修復一個故障節點，多個故障節點沒有考慮，學術界針對多個故障節點的LRC修復引入了(n,k,r,gama)-區域性修復碼，針對多個故障節點修復的區域性修復碼滿足上界如下：

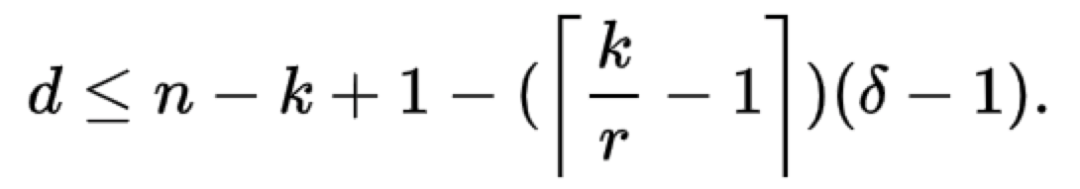
2.2.5 piggyback框架

piggyback框架嚴格意義上是MSR的一個子集，piggyback框架的核心思想是通過擴充套件後MDS碼的子條帶資料嵌入到其他子條帶的操作，在不改變原有編碼結構的情況下顯著降低修復頻寬。

例如，以一個（4，2）MDS碼如圖所示，它有兩個子條帶，每個子條帶上分別有兩個資訊資料，每個子條帶的後兩位儲存該條帶的傳輸線性組合，圖左1為MDS碼，圖左2為piggyback編碼，我們來分析一下右圖1和右圖2兩種節點故障的情況下修復頻寬的消耗情況：

（1）右圖1修復：傳統MDS碼：任意2個節點的2個符號來修復；piggyback碼：b2, b1+b2, b1+2b2+a1這三個符號可以修復a1, b1兩個符號；

（2）右圖2修復：傳統MDS碼：任意2個節點的2個符號來修復；piggyback碼：b1,b1+b2, 2a2-2b2-b1這三個符號可以修復a2,b2兩個符號。

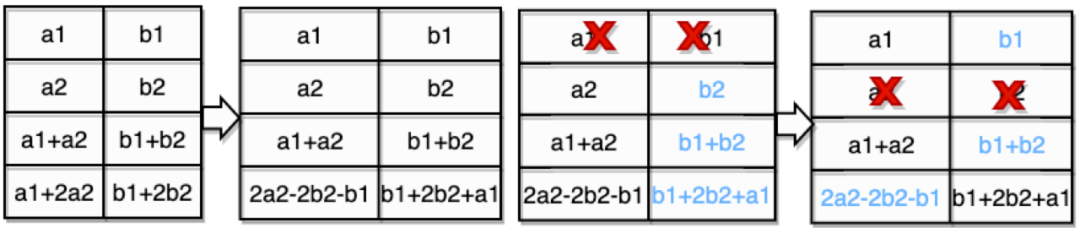
圖12：PiggyBack框架示意圖

三、糾刪碼行業探索與實踐

在第二大章節以經對當前糾刪碼幾個核心領域的編碼原理進行了闡述，本章則介紹這幾個核心領域的糾刪碼在工業界的應用。基本上每種型別的糾刪碼都或多或少在工業界有具體的編碼演演算法及實踐經驗。為了保持和第二章的順序保持一致，本章也從RS碼、陣列碼、RC、LRC、PiggyBack這幾個方向應用於工業界的具體編碼順序進行詳細介紹。

3.1 RS：CRS

首先是應用最為廣泛，也是最成熟的RS碼，當前工業界大多數的糾刪碼都是基於該編碼實現的。雖然RS碼的修復頻寬一直是一個痛點，但是由於其基本上每家公司的最早的糾刪碼演演算法上線都是基於RS完成的。比如早期的Google、AWS、阿里、騰訊、華為、百度等公有云廠商。

3.2 陣列碼：HashTag

An alternate construction of an access-optimal regenerating code with optimal sub-packetization level

3.3 MSR：Butterfly

butterfly是FAST 2016年的一篇論文提出的編碼演演算法，最多可校正2個節點故障的資料丟失，演演算法只涉及XOR操作，效能較好。節點故障後只需要所有節點的1/2資料引數修復。由於編碼操作用線相連對應符號位看起來像蝴蝶一樣，如下圖所示，所以取名butterfly code。

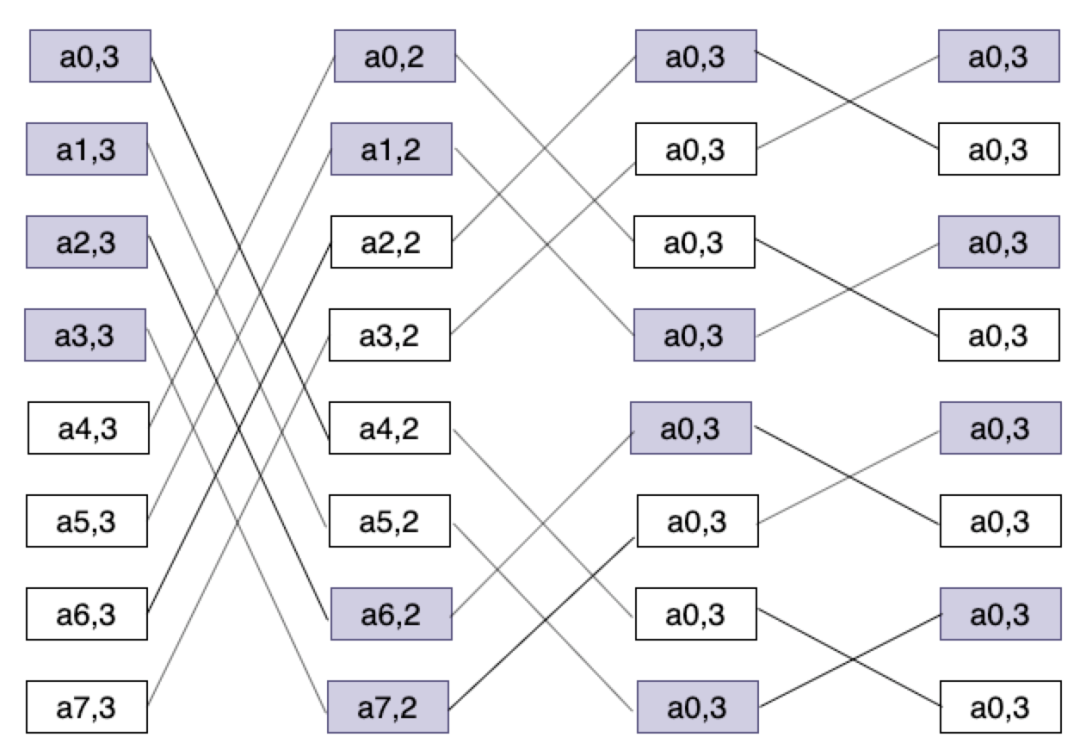
圖13：Butterfly碼示意圖

編碼方法：

首先資料符號需要轉換成一個bit矩陣2^(k-1) * k記為Dk，用矩陣表示如下：

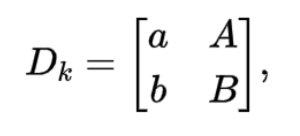
其中，A,B是2^(k-2) * (k-1)的bit矩陣，a,b則是一個包含2^(k-2)個元素的列向量。如果把 butterfly編碼後的碼字記為：Ck = (Dk−1 k ,...,D0 k ,H,B),則不難看出，H,B分別帶為butterfly後的一個水平校驗列和butterfly校驗列。H,B的生成遵循如下遞迴準則：

如果 k = 2，那麼有：

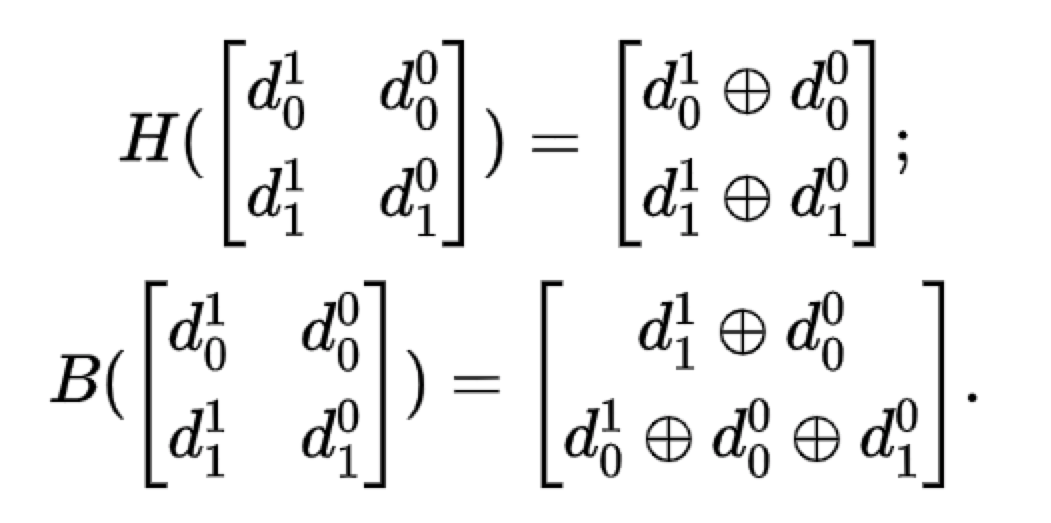
如果 k > 2，那麼有：

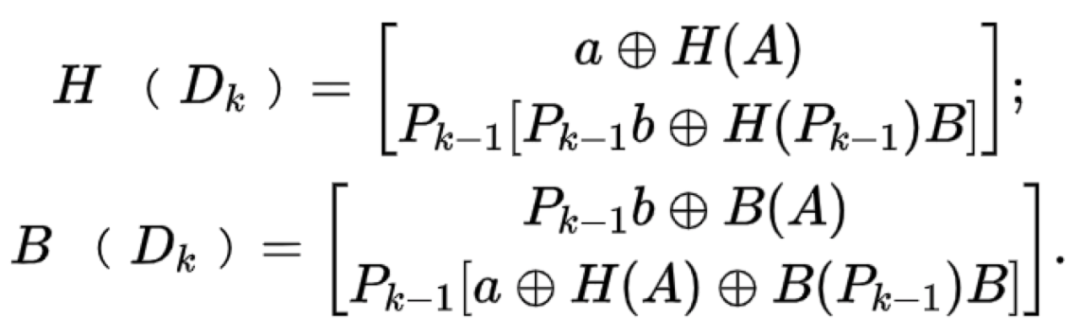
其中，Pk帶表一個包含2^k * 2^k個元素的矩陣，矩陣的副對角線元素為1，其餘元素為0。下圖為一個k = 4的 butterfly編碼：

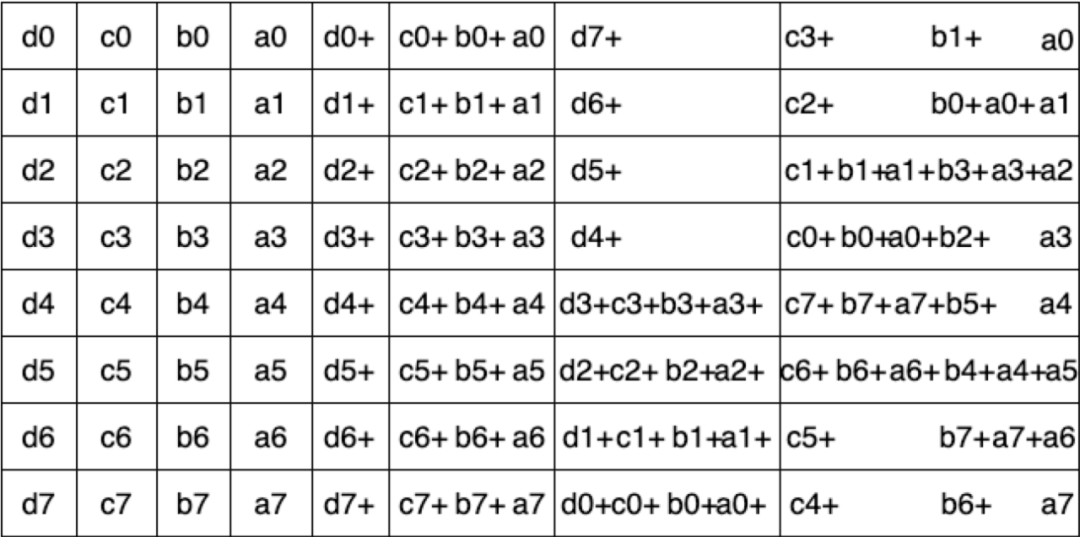
圖14：k=4 Butterfly編碼構造

3.4 MSR：Clay

Clay碼是FAST 2018年的一篇論文提出的編碼演演算法，Clay碼能夠將一般的MDS碼轉化為MSR碼，Clay碼包含兩個特點：1 將MDS碼分層處理；2 分層之間資料耦合，以（4，2）Clay碼為例，為了更形象瞭解編碼方式，將編碼後的資料放在稜形柱上，其中alpha = 4，也就是有4層，原始資料如下：

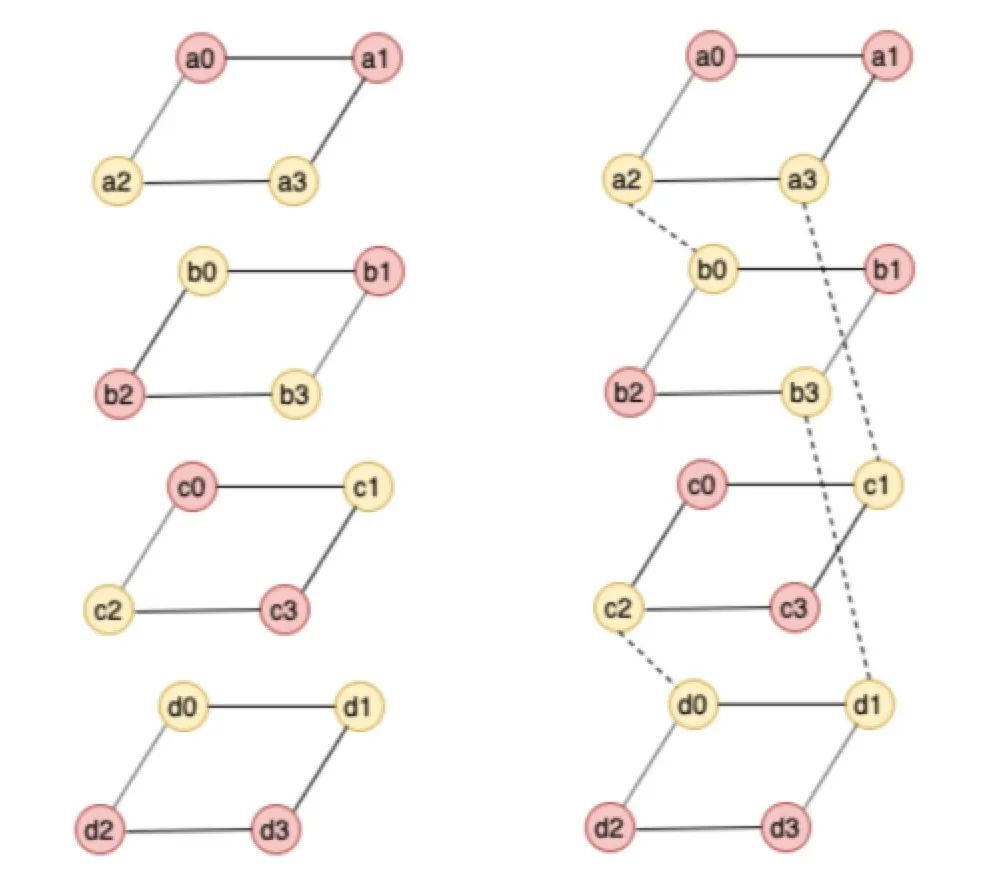
圖15：原始資料結構

圖中被耦合的資料用黃色表示，耦合關係如上圖右虛線表示，黃色資料塊儲存的是耦合之後的資料，也就是不再是系統碼，相當於解碼需要進行解耦合才能得到原始資料。

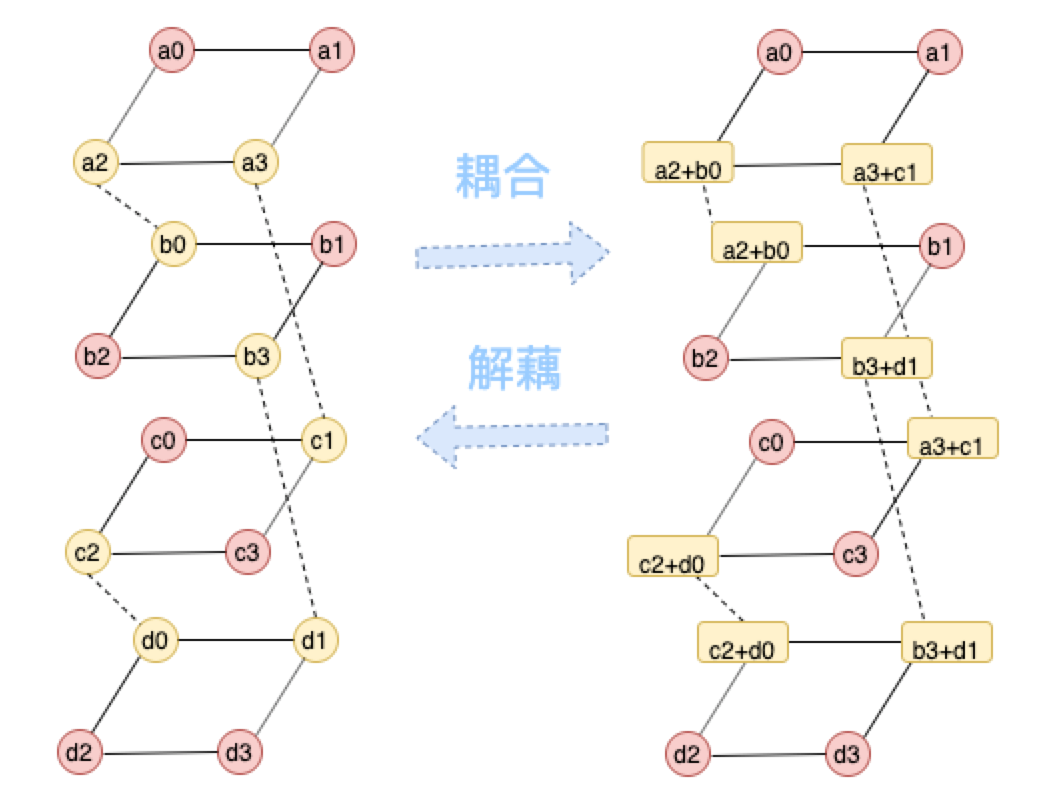
圖16：CLAY編碼結構

當有一個節點失效後，CLAY碼的修復過程如下：

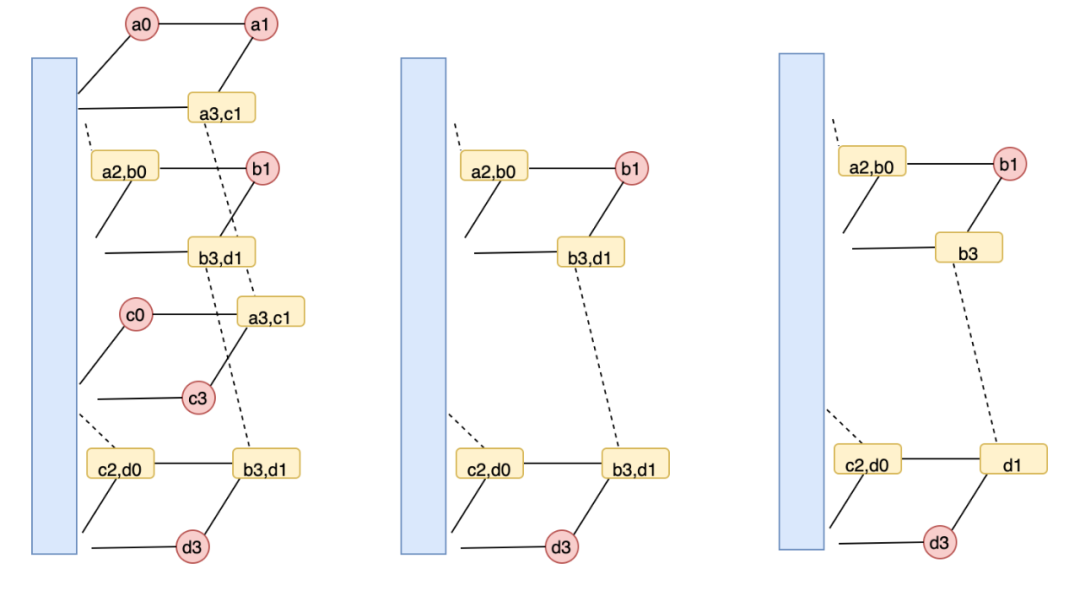
圖17：CLAY修復結構

Clay 修復該節點失效只需要第二層和第三層的剩餘資料塊（如上圖（中）所示），修復步驟如下：

• 兩個耦合的資料塊(b_3,d_1) 和[b_3, d_1] 解耦得到b3 和d1，如上圖（右）；

• 第二層通過b1，b3 的MDS 解碼得到b_0, b_2，第四層MDS 解碼得到d_0，d_2；

• 利用第二層中[a_2, b_0] 和步驟2 得到的b_0 得到a_2，同理得到c_2。

簡單推導可以發現其他三個節點也可以以最小開銷完成資料修復。

3.5 LRC：azure、yottachain LRC

區域性可恢復碼LRC是微軟在2012年FAST發表的一篇論文，該論文同時也是當年FAST的best paper。核心思路就是通過引入區域性校驗位來輔助全域性校驗位進行節點故障後的修復，由於區域性校驗節點的存在，所以當有一個節點故障的時候可以只用區域性少數節點進行恢復，而不需要全域性節點進行恢復提升修復頻寬。以下以（6，2，2）LRC為例進行介紹：

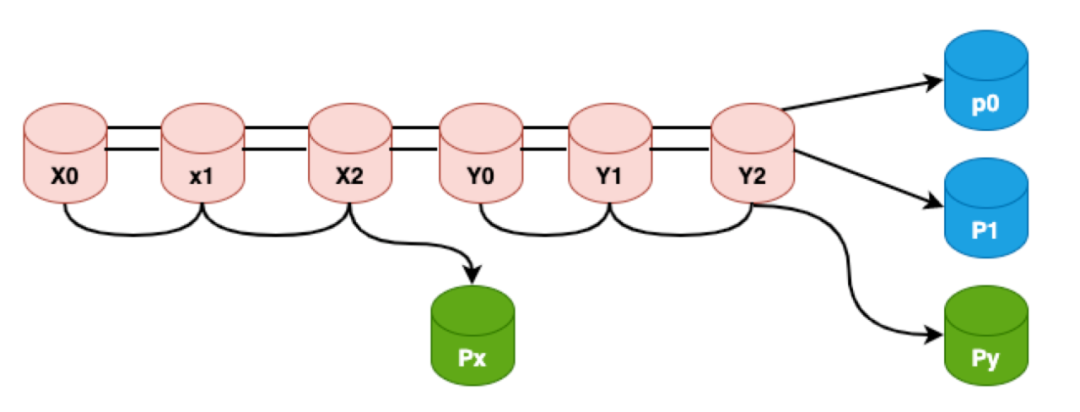
圖18：全域性&區域性校驗示意圖

如上圖所示px,py為區域性校驗節點，p0,p1為全域性校驗節點，不難看出，雖然LRC有4個校驗節點，但是LRC不滿足MDS性質，比如x0,x1,x2,px 4個節點全都故障，LRC無論如何校造都是無法恢復的，因為全域性校驗節點只有2個，而py和x0,x1,x2無關，所以無論如何都恢復不出來x0,x1,x2這三個資料節點，這種故障也稱為資訊理論無法解碼故障；雖然LRC不能容忍這種場景的4個節點故障，但是如果LRC構造得好，是可以達成其它場景的4個節點的故障，比如下圖所示：

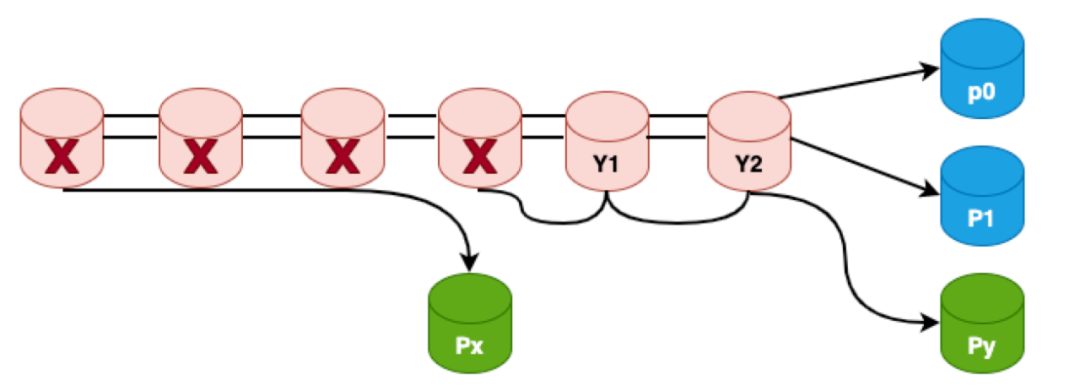
圖19：4資料節點失效示意圖

a圖是x0,x1,p1三個節點故障，b圖是x0,x1,y0,y1四個節點故障，這類故障是有可能重建的也稱為資訊理論可解碼故障。那麼LRC的研究就是設計合理的編碼方式來儘可能的覆蓋所有資訊理論可解碼故障場景，當LRC的構造方式覆蓋了所有資訊理論可解碼場景則稱LRC碼符合Maximally Recoverable（MR）性質。 (6，2，2)的校驗位構造方程如下：

 

 

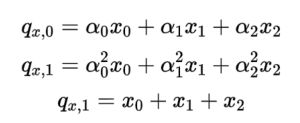
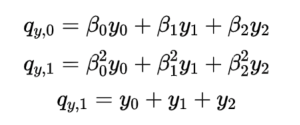
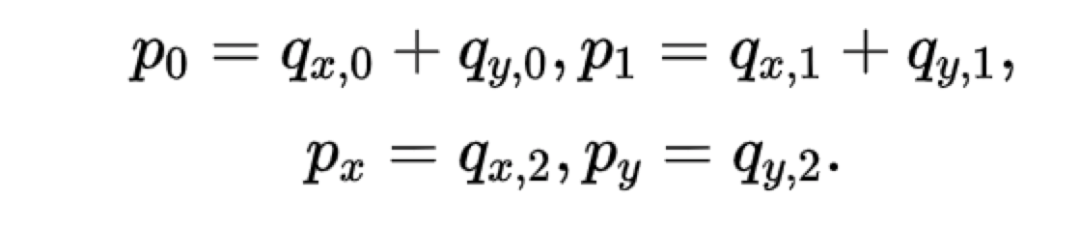
然後該編碼構造方法需要覆蓋所有理論可解碼故障場景比如以下三種典型場景：

（1）4個節點全故障，平均分佈在6個資料節點

這種場景則不難看出要想可求解就必需保證：

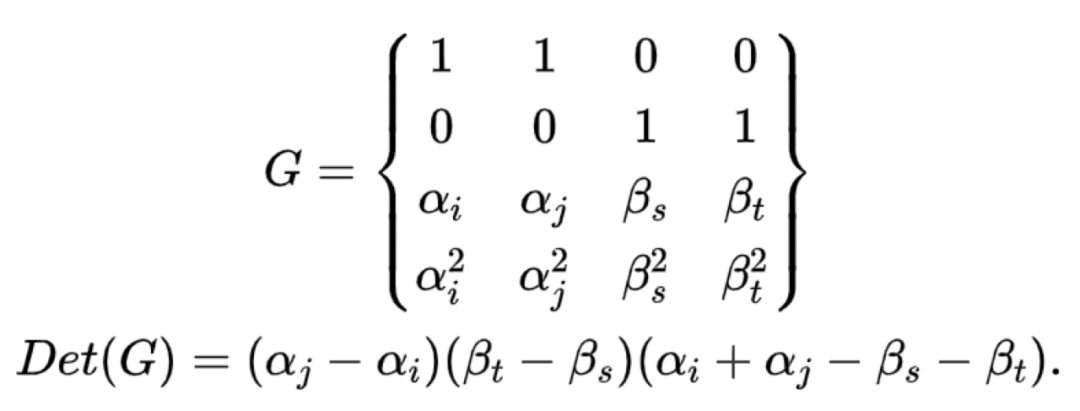
G的行列為不為0，G矩陣是奇異矩陣。

（2）px,py中有一個故障，假設是py故障，則必須有：

 

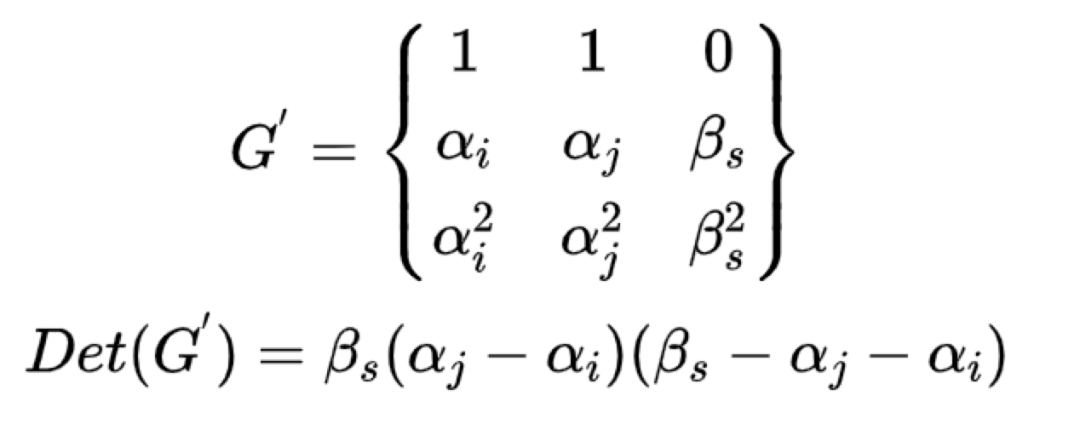
（3）同理如果px,py全故障，則必須有：

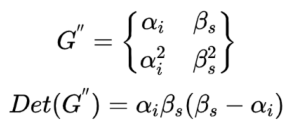
因此，alpha，belta的取值必須滿足上述矩陣的行列式不為0。（6，2，2）LRC與（6，3）的RS對比不難發現：LRC可靠性略高，成本也略高，修復頻寬幾乎是原來的一半。

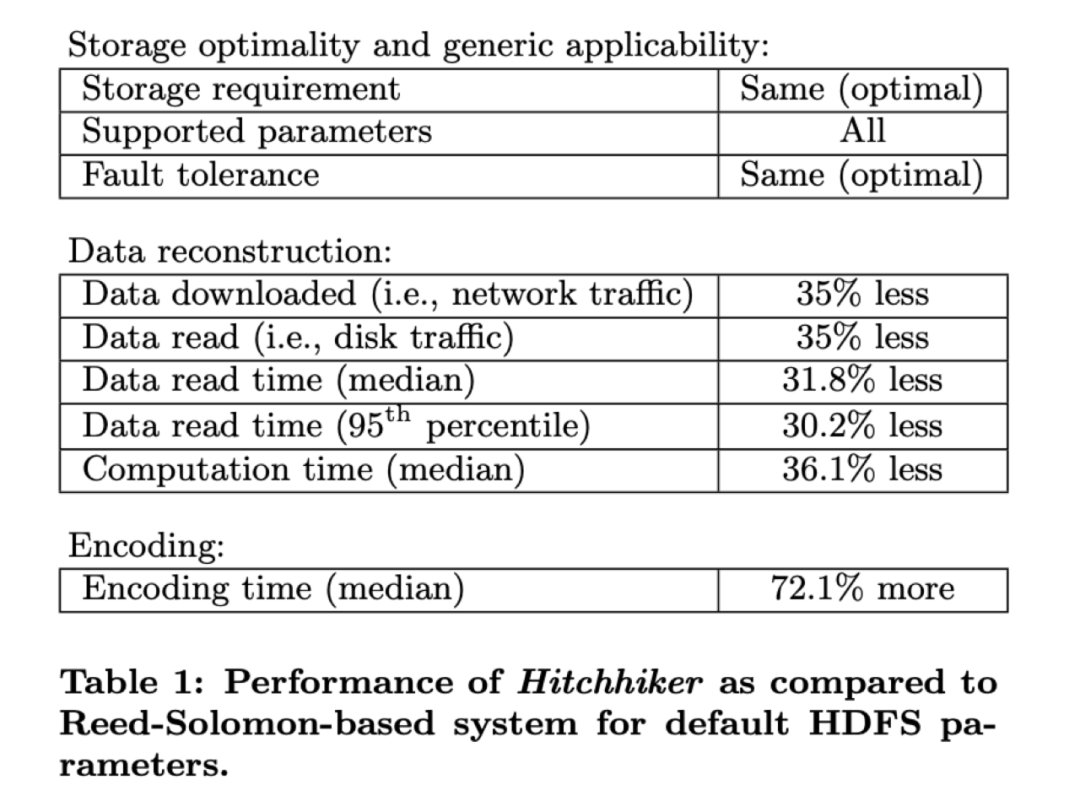
3.6 piggyback：Hitchhiker

piggyback框架的一個典型的工業界的應用實踐場景是facebook在2014年提出的，當時facebook的f4系統原本也是用（10，4）RS糾刪碼來降低冗餘度，但是RS碼的修復頻寬非常高，據當時統計資料，facebook一個PB級的叢集中因為節點恢復所需要消耗的網路頻寬達到了180TB。所以facebook針對冷存叢集提出了一種基於piggyback框架的Hitchhiker編碼來降低修復頻寬。

（1) Hitchhiker-XOR

傳統的(10,4)的RS編碼如下圖左1所示，引入piggyback框架後則編碼方式如下左2所示，Hitchhiker-XOR編碼方式如下右1所示：

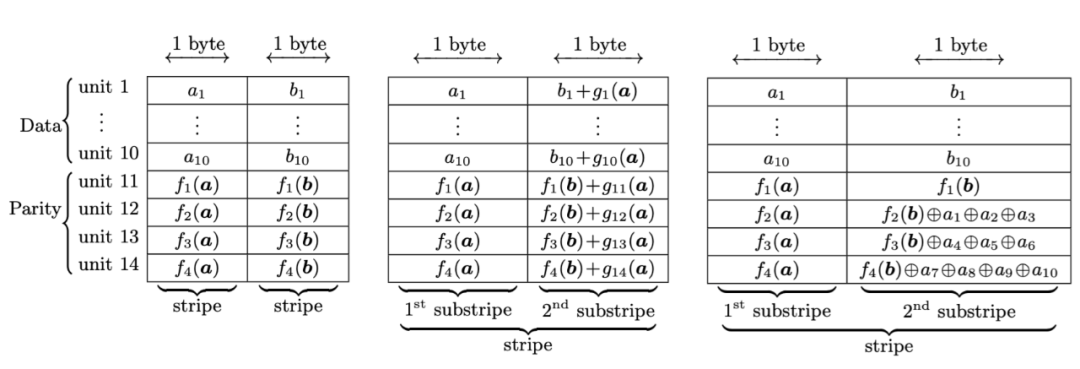
圖20：Hitchhiker-XOR編碼示意圖

編碼：4個校驗單元：f1保持不變，f2引入a1,a2,a3的奇偶校驗位，f3引入a4,a5,a6的奇偶校驗位，f4引入a7,a8,a9,a10的奇偶校驗位。

修復：當1-3有一個節點故障，則可以通過，b1-10,f1(b)中的任意10個但願恢復出故障的bi，然後可以通過f2函數計算出f2(b)，再結合第2個子條帶的第2個校驗單元以及a1-a3中的2個單元一起，可以計算出ai，這樣就把ai,bi修復出來了。 同理，當4-6有一個節點故障時，也是一樣的，可以通過13個byte將ai,bi進行恢復。

而當7-10有一個節點故障時，則需要通過14個byte進行恢復，原因是第2個子條帶的第4個校驗單元是由a7,a8,a9,10四個組合，其中有一個失效，需要引入第1個子條帶的3個單元才能進行恢復。

（2）Hitchhiker-XOR+

針對Hitchhiker-XOR演演算法，可以看到在第7-10節點故障時需要14個Bytes進行修復，XOR+通過對RS碼進行適當限制來降低這一部分的開銷，限制條件如下：4個校驗單元的函數f需要有一個滿足：ALL-XOR性質，也就是子條帶資料全部進行互斥或操作的同時滿足MDS性質。通過該限制，則兩個子條帶的校驗單元的編碼方式如下圖所示：

圖21：Hitchhiker-XOR+編碼示意圖

修復： 

不難看出，1-9節點故障時的修復是和Hitchhiker-XOR是完全一樣的，只需要13個bytes進行修復，第10個節點故障時，則通過第2個子條帶的1-10，13，14單元和第1條帶的12單元可以恢復a10,b10，不難看出，恢復節點10也只需要13個bytes。

所以Hitchhiker-XOR+相對於Hitchhiker-XOR限制了RS碼構造的條件，但進進一步降低了部分資料修復的開銷。

（3）Hitchhier-NoXOR

這種編碼是針對於Hitchhier-XOR+是引入了限制條件，為了消除這個限制條件，可以通過有限域運算的方式來達到Hitchhier-XOR+同樣的效果，但是可以消除RS的校驗生成限制，與此同時也是通過有限域運算開銷來替換XOR操作。

圖22：Hitchhier-NoXOR編碼示意圖

以上編碼方式可以擴充套件到任意的(k,r)，對於不同的k,r引數，HH碼相對傳統RS碼可以降低25%-45%不等的開銷。

3.7 糾刪碼對比

（n,k）糾刪碼，資料大小為M，劃分為k份，生成m份校驗資料 k + m = n，則相關糾刪碼演演算法的相關開銷和性質總結如下：

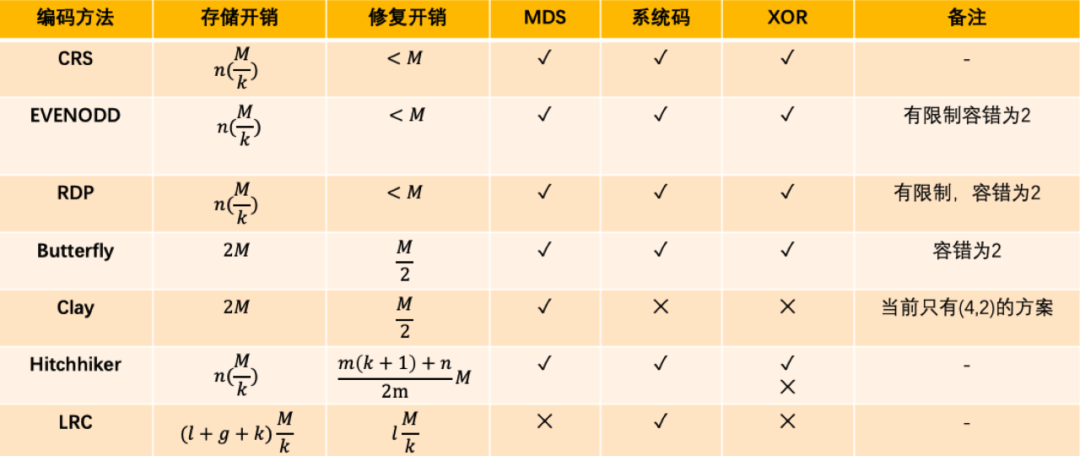
圖23：糾刪碼演演算法相關維度對比

四、vivo 糾刪碼探索與實踐

4.1 線上EC方案介紹

vivo物件儲存的EC方案是採用RS糾刪碼，前面章節已經介紹過RS碼是通過構造生成矩陣來編碼資料塊。生成矩陣可以採用範德蒙德矩陣，原因是因為範德蒙德矩陣是可逆的，另外，還有一種矩陣是也可逆矩陣那就是Cauchy矩陣，Cauchy矩陣是由兩個交集為空的集合構成的矩陣，具體為：令C = [c(i,j)]m*n，有集合X = {x1,x2,...xm}，Y = {y1,y2, ...,yn}，且X交集Y={空}。矩陣C中的元素cij滿足：

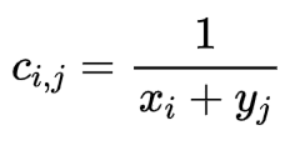
不難理解，如果不做優化，柯西編解碼過程會充斥著大量的有限域的乘法和加法運算，為了降低複雜度，通過利用有限域任何一個GF（2^w）域上的元素都可以對映到GF(2)域上的一個二進位制矩陣，例如，GF(2^3)域中的元素可以表示成GF（2）域中的二進位制矩陣：

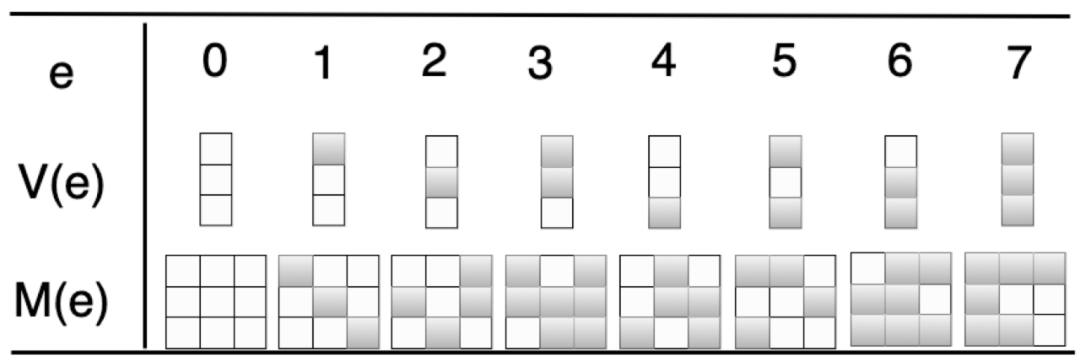
圖24：GF(2^3)在GF(2)對映矩陣

其中，M ( e )的第i 列為V ( e ∗ 2^ (i − 1 )) 其中e ∗ 2^(i-1) 為G F ( 2 ^3 ) )上的乘法。

所以基於Cauchy矩陣的RS編碼方案可以優化為bit-matrix為生成矩陣，原有的有限域上的乘法和加法也變成了有限域的「與運算」和「XOR」運算，從而提高編碼效率。

在真正實現的時候， vivo糾刪碼的CRS編碼和jeasure的CRS編碼一樣，針對bit-matrix在GF(2)有限域的與和OXR操作進行也進一步優化，就是通過將bit-matrix轉化為一個schedule的方式，也就是一個五元組，其中，op操作是O,1對應是拷貝還是XOR，sd是源資料的id，sb為源資料中bit位的相對id，dd和db則為目的校驗資料的id和校驗資料bit位id。如下圖針對一個k = 3, w = 5的bit-matrix對應的schedule操作為如下：

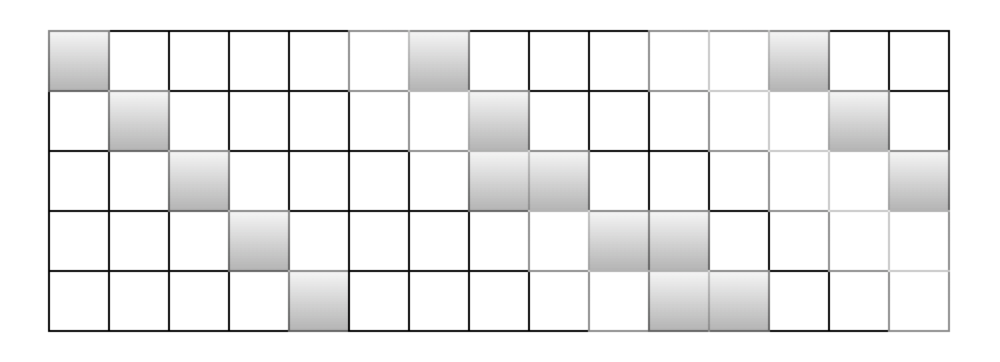
圖25：bitmatrix的schedule操作

不難看出，通過schedule方式轉化後編解碼操作簡化了好多，以下為一段C++程式碼：

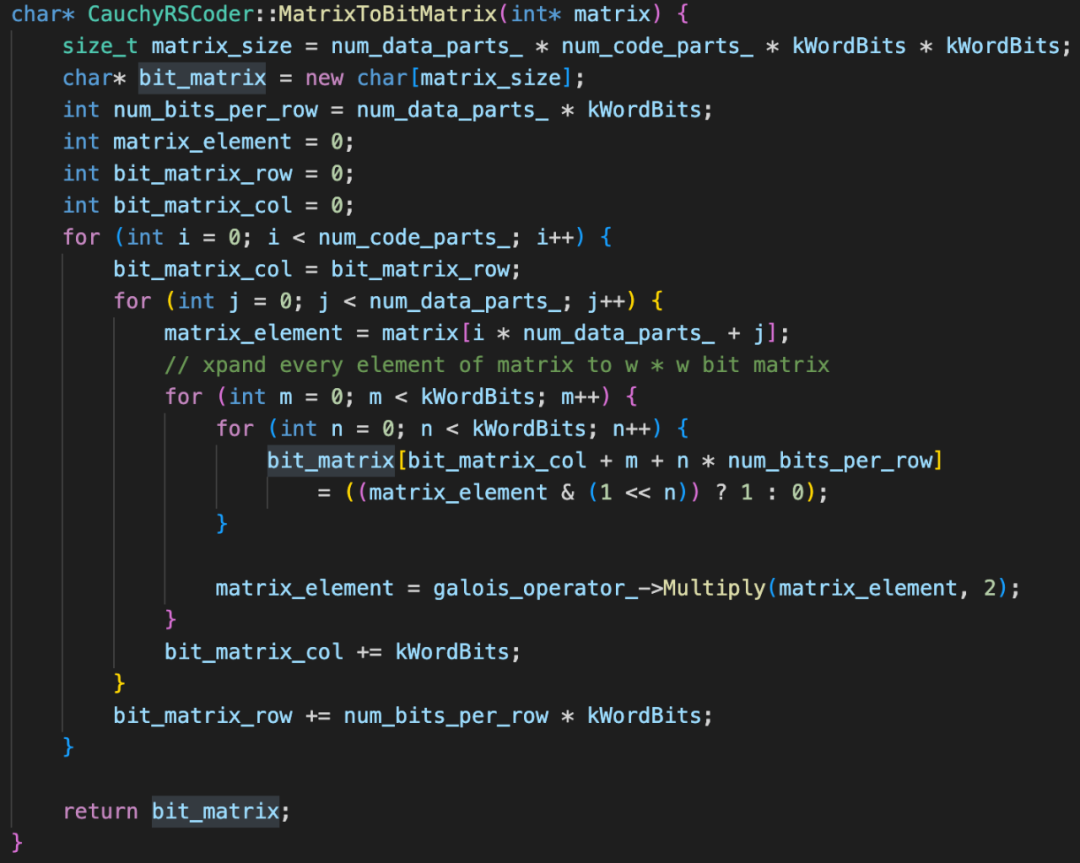
圖26：儲存糾刪碼schedule程式碼片斷

4.2 生產環境分析

注：這裡的生產環境分析章節是參照常規的業界生產環境部署規範進行假設和模擬，不代表本公司的真實生產環境。

4.2.1 IDC資源

現在很多公司為了能夠防止資料中心因為某些不可抗力比如自然災害、斷電等極端情況導致整體故障而造成資料丟失和服務中斷建設了多個資料中心，分散式儲存服務可以通過將資料打散儲存在多個不同的資料中心來保證當某個IDC故障後依然能提供穩定可靠的儲存服務。糾刪碼技術通過將資料分塊和校驗碼分塊均勻打散到不同資料中心，實現同城容災冗餘。當某個資料中心不可用時，另外其他資料中心的資料依舊可以正常讀取和寫入，保障客戶資料持久儲存不丟失，維持客戶業務資料連續性和高可用。

以下為一個同城冗餘的示意圖【參照自公有云多region多AZ機構】

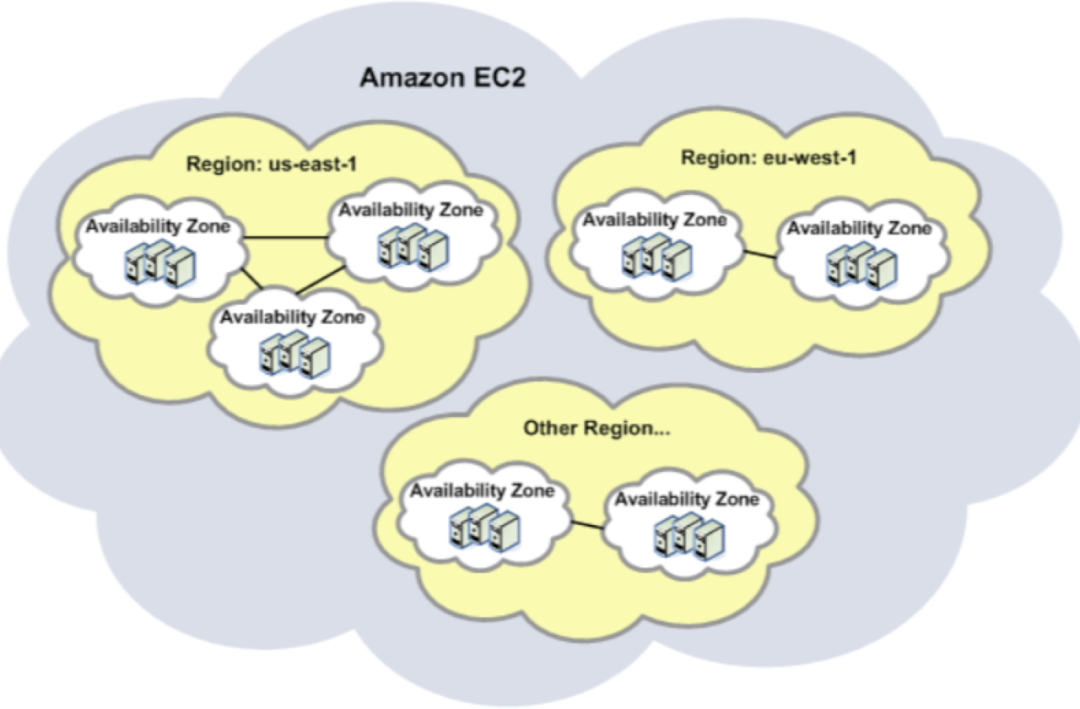
圖27：同城冗餘機房示意圖

4.2.2 儲存資源

隨著近年網際網路業務的非速發展，網際網路業務資料的規模及多樣性也越來越複雜，各大公司的儲存型伺服器由於歷史原因迭代過很多的版本，從4xTB到1x00TB容量不等的演進了有多種套餐型別，因此生產環境很難避免的有多種儲存型別的伺服器共存的情況出現，伺服器的攜帶的HDD硬碟的塊數和單盤的容量也不盡相同，單盤容量從4T到20多T不等，伺服器攜帶的硬碟數目也從12到60多不等，還有各種其它型別的儲存陣列比如JBOD產品（由多塊60TB的硬碟組成的儲存資源陣列）。

4.2.3 網路資源

如第1章所述，糾刪碼技術在海量分散式儲存系統的引入為企業節省了大量的成本，但是在節約成本的同時，由於糾刪碼技術特點也帶了頻寬成本的上升，基於糾刪碼冗餘的分散式系統在出現節點或硬碟故障時，需要多個節點進行同時恢復，這就需要大量的網路硬碟頻寬，而且以（n,k）RS碼為例，1個RS碼的節點故障，需要n個節點進行恢復，而副本技術的系統只需要1個節點參與，相當於糾刪碼技術的系統網路頻寬放大了n倍速。因此，在IDC內部和IDC機房之間的頻寬就成為了糾刪碼技術實施的關鍵因素。

以下為業界某司的IDC之間的網路拓撲架構如下：【參照自公有云多region多AZ機構】

圖28：業界IDC頻寬拓撲架構

而由於成本上的考慮，往往資料中心與資料中心之間的專線頻寬都不會太高，但是傳統的糾刪碼技術在提供低冗餘度和高可靠的同時帶來的是大理的修復頻寬的成本，因此，跨IDC之間的糾刪碼技術不得不考慮IDC之間的頻寬不大這個因素。

4.2.4 業務特性

• 物件儲存業務特點1：通常接入物件儲存的大規模業務的更新的操作比較少，因此原有的更新的操作消耗頻寬成本高的痛點可以不考慮；

• 物件儲存業務特點2：通常接入物件儲存業務線上場景和離線場景區分比較明顯；大儲存業務呈現冷資料趨勢；

• 物件儲存業務特點3：網際網路行業的資料型別豐富，一般對跨AZ和不跨AZ的需求有所不同，資料可靠性的要求各有不同；可用性指標各有不同。

4.3 vivo新糾刪碼方案

4.3.1 糾刪碼優化思路

• 基於糾刪演演算法思考：通過對學術界和工業界的整體調研考慮實現複雜度和效果發現還是RS碼還是當前工業界糾刪碼的主流，特別是對RS碼引入並行修復後非常的適合降低跨IDC之間的頻寬消耗；可以將大部分的頻寬消耗收斂到IDC內部；

• 基於機房資源思考：基於多資料中心的資料分佈考慮，糾刪碼可以考慮引入LRC，在資料中心內部引入區域性校驗塊來進行資料中心內部的快速修復從而提高整體可靠性；

• 基於業務特性思考：根據網際網路業務的通用特性分析可以將離線線上儲存叢集進行分離；以及資料可靠性要求進行規劃EC叢集，比如不考慮機房容災的業務可以在同一個資料中心內部的不同Region進行部署EC叢集；

• 基於服務資源思考：網際網路行業的儲存伺服器資源的儲存和網路卡設定迭代較快，線上這種異構環境導致的線上擴縮容操作都會引起叢集可靠性的變化，因此引入可靠性評估模型對叢集進行近實時的預估；

• 基於恢復頻寬思考：優化目標是為了進一步降低EC冗餘度但同時可靠性不降低，因此恢復頻寬降低是一個重要優化思路，因此在全域性引入並行修復和在區域性引入MSR糾刪修復的方式進一步降低恢復頻寬。

4.3.2 可靠性模型設計

在優化思路我們提到引入可靠性評估模型來對叢集進行近實時的預估，那麼可靠性模型如何預估是合理的？當前並沒有一個統一的可靠性評估方案，不過學術界基本都是基於馬爾可夫鏈的MTTDL模型來進行EC的可靠性計算，工業界就沒有特別統一的可靠性評估方案，在調研了行業內相關方案後我們的可靠性模型主要是基於MTTDL馬爾可夫鏈模型再結合我之前分享的一篇【分散式儲存系統的可靠性估算】形成特有的分散式儲存可靠性模型估算方案。這套方案是結合了兩種可靠性估算最合理的部分邏輯：MTTDL模型的理論嚴謹性 + 叢集級磁碟故障的組合概率引入的必要性。

在介紹可靠性模型之前，我們先來看幾個概念如下圖所示：

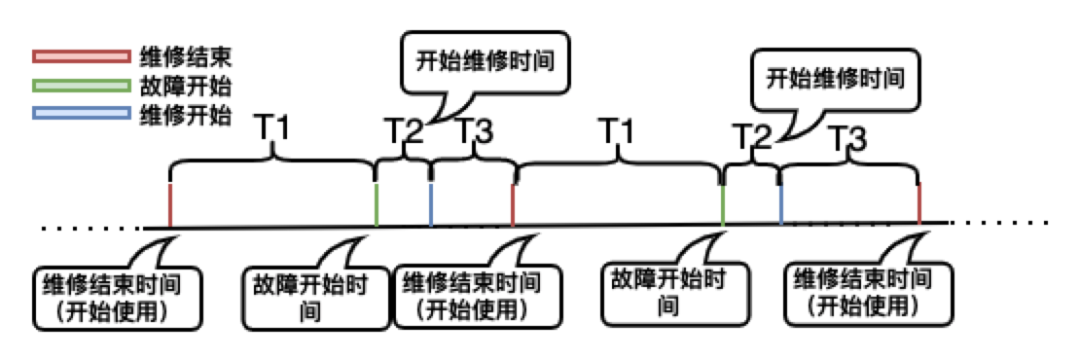
圖29：系統故障處理流流程【時間線】

• MTTF：Mean Time To Failure，平均無故障時間，指系統無故障執行的平均時間，取所有系統開始正常遠行到發生故障之間的時間段的平均值，如上圖的T1的平均值；

• MTTR：Mean Time To Repair，平均修復時間，指系統從發生故障到維修結束之間的時間段的平均值。如上圖的T2+T3的平均值；

• MTTDL：Mean Time to Data Loss，平均資料丟失時間，換個說法也可以是系統兩次故障發生時間的間隔平均值，如上圖的T1+T2+T3的平均值。

（1）Markov可靠性模型

Markov可靠性模型是基於MTTDL進行預估的，Markov可靠性模型是基於下圖來進行狀態轉移的：

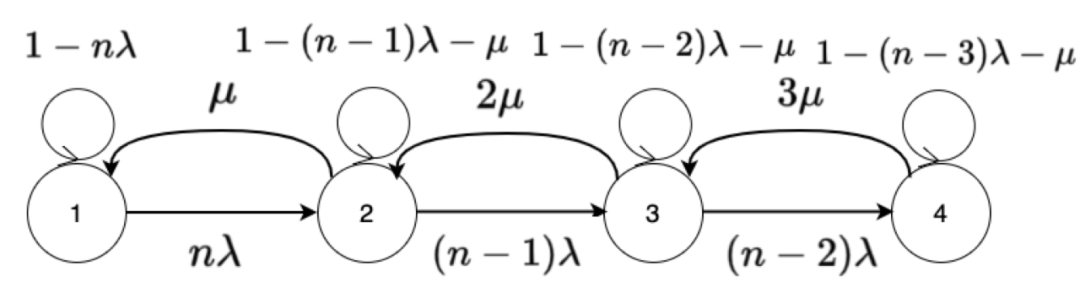
圖30：馬爾科夫鏈的故障狀態轉移模型

初始狀態為1狀態，1狀態為n塊磁碟都沒有故障的概率為1-n* ramda，從狀態1轉移到狀態2則是有n*ramda概率，狀態2恢復到1狀態則由u決定，狀態2轉移到狀態3的概率為1-(n-1)* ramda，則不難計算出維持2狀態的概率如上圖所示：

本文不對馬爾科夫鏈狀態轉移進行詳細推導，僅給出最終的MTTDL的簡化版計算公式如下：

 

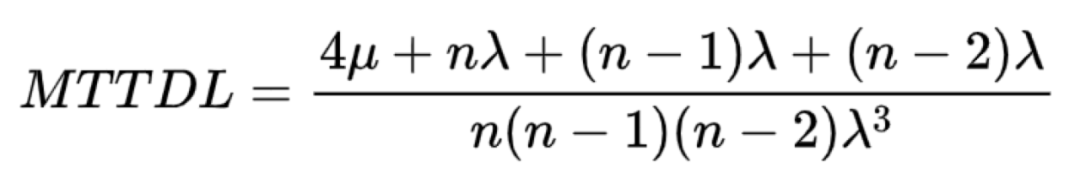
（2）其它可靠性模型

Markov可靠性模型是把所有磁碟都用在了資料的條帶化處理，但是真實的線上環境叢集可能非常龐大，整個叢集的節點數會遠大於進行糾刪碼的n的大小，那麼從叢集角度看可靠性如何估算呢？我曾經在21年有發表過一篇外發期刊【分散式儲存系統可靠性：系統量化估算】，這篇文章就是以生產環境以叢集部署的角度進行分析分散式儲存系統的可靠性如何估算，這篇文章相對於Markov可靠性模型一個最大的借鑑意義是它把叢集內的一個資料的條帶化組合引入到了可靠性估算，因此，新的可靠性估算模型可以結合Markov可靠性模型和叢集條帶化組合比例進行設計，更加具體的設計方案會在【糾刪碼技術在vivo儲存系統的演進-下篇】中介紹。

4.3.3 多融合EC方案設計

根據對IDC資源、伺服器資源、業務特性、網路資源的分析，結合可靠性評估近實時系統的支撐，我們在原有的8+4 CRS糾刪碼演演算法的基礎上進行優化，將整體的EC策略分為兩種如下圖所示：

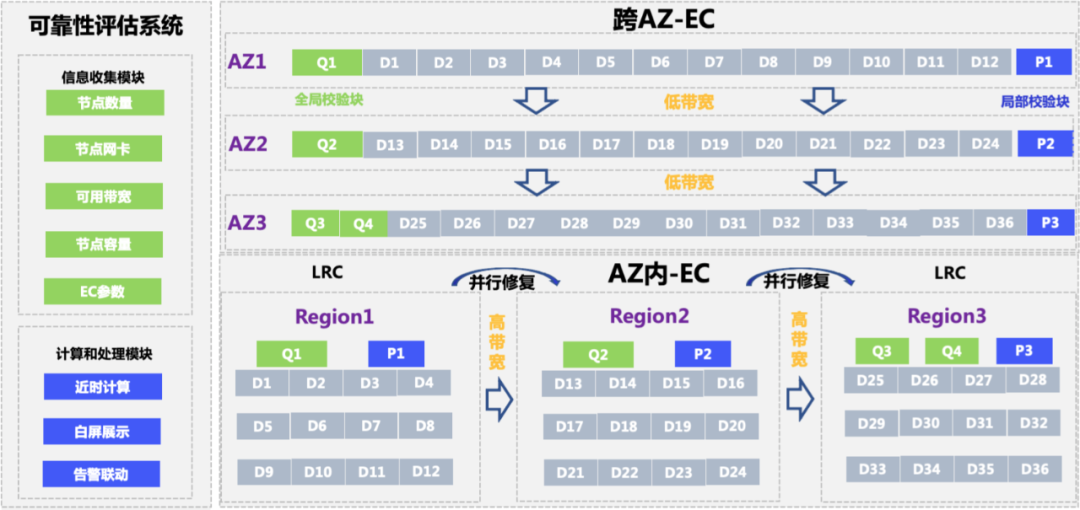
圖31：多融合EC方案架構圖

跨AZ-EC策略

核心業務資料有跨AZ儲存需求進行機房資料容災，但是同時也帶來在節點故障情況下有跨機房網路頻寬的影響，因此EC策略是LRC+RS+並行修復+MSR結合的EC方式，針對不同的場景有不同的優化措施：

• 當只有一個資料節點故障情況下，通過在各機房的區域性校驗塊，只需要在機房內用MSR最小頻寬進行快速修復；

• 當只有一個區域性校驗節點故障下，也是通過在各機房的資料塊在機房內進行快速修復；

• 當只有一個全域性校驗節節點故障下，則可以通過一個機房的區域性校驗塊再結合其它機房的中間結果資料進行並行恢復；條帶越寬，頻寬節省越多，比如單機房12資料塊，3機房可節省跨機房頻寬80%+；

• 當有兩個或兩個以上節點同時故障的情況下，才需要進行跨機房傳輸資料修復，我們可以通過區域性校驗塊+其它機房中間結果結合+並行修復的形式來降低網路頻寬消耗。

為了能描述清楚我們的策略，我們以（16，4，4）4機房，4個區域性校驗塊，4個全域性校驗塊，16個資料塊【如下圖所示】為例來說明：

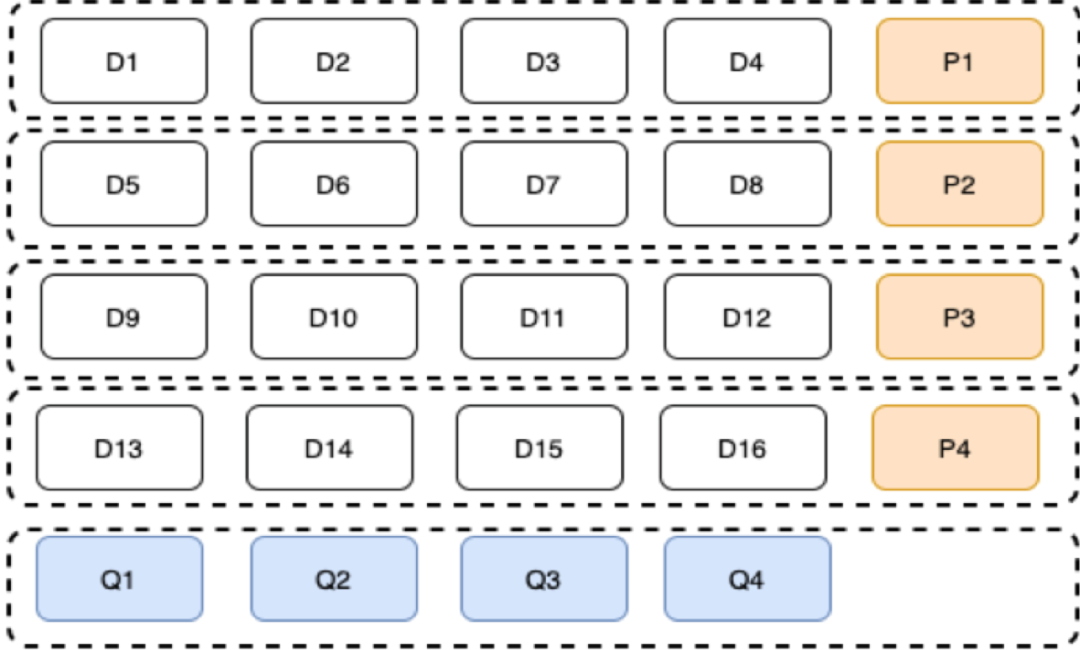
圖32：（16，4，4）LRC編碼拓撲

我們假設區域性校驗塊P1、P2、P3、P4的構造按如下所示：

同樣按RS碼構造方式，我們假設Q1、Q2、Q3、Q4的構造按如下所示：

接下來我們來分析一下不同場景下的恢復情況：

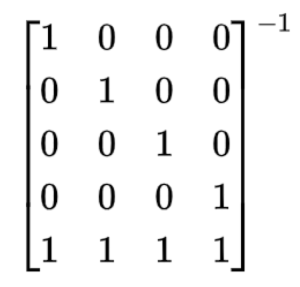
• 只有一個資料節點或P節點故障：只需要在每個區域性進行即可，利用生成矩陣的逆矩陣：

• 只有一個Q節點故障：按原來的演演算法是需要D1-16全部參與進行計算，但是我們分析可以發現生成矩陣是固定的，因此，完全可以在機房內部進行中間運算後再傳送到故障機房進行最終運算得到，以Q2為例，只需要以下四個生成矩陣在各自機房與機房資料Di進行中間結果運算即可：

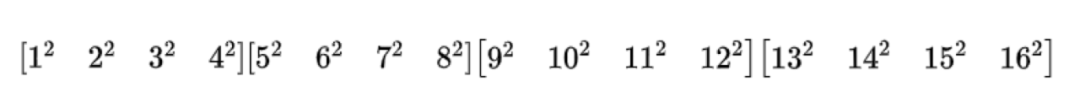
• 有兩個或兩個以上節點故障：可以通過在叢集執行前先把所有可能的校驗矩陣【如下圖所示】準備好，然後再通過在各自機房與機房資料Di或Qj進行中間結果的計算，最後在需要恢復機房進行最終結果的合併計算得到恢復資料：

具體演演算法的詳細細節會在後續的【糾刪碼技術在vivo儲存系統的演進-下篇】介紹，整體思路就是全域性RS+並行修復結合區域性MSR最小頻寬修復的策略來達到多AZ資料可靠性保障的目標。

五、總結

雲端儲存領域針對糾刪碼技術的研究截止到現在仍然是學術界和工業界研究的熱點，如何能降低網路的修復頻寬，降低儲存開銷同時保證資料的可靠性的同時編解碼演演算法又能工程落地，編解碼複雜度又偏低，這些維度的考量衍生了各式各樣的糾刪碼編碼技術，vivo也在糾刪碼技術根據生產環境可落地的前提下在傳統RS碼的基礎上引入並行修復以利用LRC+MSR區域性校驗塊的組合來降低傳統LRC在生產環境上運用導致的跨機房頻寬開銷，從而較低的跨機房頻寬開銷為高條帶低冗餘度的EC策略提供了保障。隨著業務的發展，資料的儲存開銷成本會越來越明顯，因此，針對糾刪碼技術的研究會是一個長期的過程，本人也會時刻關注學術界和工業界的動態，結合IDC、伺服器、網路及業務的特性進行創新和優化為業務持續助力。

 

參考文獻：

1. Reed I S, Solomon G. Polynomial Codes over Certain Finite Fields. Journal of the society for industrial and applied mathematics, 1960, 8(2):300-304

2. Plank J S, Ding Y. Note: Correction to the 1997 tutorial on Reed-Solomon coding.Software: Practice and Experience, 2005, 35(2):189-194

3. Shokrollahi A. LDPC codes: An Introduction. Technical report, 2003.

4. Blaum M, Brady J, Bruck J, et al. EVENODD: An Efficient Scheme for Tolerating Double Disk Failures in RAID Architectures. IEEE Transactions on computers (TOC), 1995, 44(2):192-202.

5. Corbett P, English B, Goel A, et al. Row-diagonal Parity for Double Disk Failure Correction. in: Proceedings of The 2nd USENIX Conference on File and Storage Technologies (FAST'04), Berkeley, CA, USA, March 31 - April 2, 2004, 1-14.

6. Huang C, Xu L. STAR: An Efficient Coding Scheme for Correcting Triple Storage Node Failures. IEEE Transactions on Computers (TOC), 2008, 57(7):889-901.

7. James S. Plank: The RAID-6 Liberation Codes. FAST 2008: 97-110

8. I. Tamo, Z. Wang, and J. Bruck, 「Zigzag codes: MDS array codes with optimal rebuilding,」 IEEE Trans. Inf. Theory, vol. 59, no. 3, pp. 1597–1616,2013.

9. Blaum M, Roth R, New array codes for multiple phased burst correction. IEEE Trans on Inform Theory, 1993,39(1): 66 ~ 77.

10. A. Dimakis, P. Godfrey, Y. Wu, M. Wainwright, and K. Ramchandran, 「Network coding for distributed storage systems,」 IEEE Trans. Inf. Theory,vol. 56, no. 9, pp. 4539–4551, Sep. 2010.

11. M. N. Krishnan and P. V. Kumar, 「On MBR codes with replication,」 in Proc. IEEE International Symposium on Information Theory, Barcelona, Spain, 2016, pp. 71–75.

12. N. B. Shah, 「On Minimizing Data-Read and Download for Storage-Node Recovery,」 IEEE Communications Letters, vol. 17, no. 5, pp. 964–967, 2013.

13. K. Rashmi, N. Shah, P. Kumar, and K. Ramchandran, 「Explicit construction of optimal exact regenerating codes for distributed storage,」 in Proc. 47th Annu. Allerton Conf. Communication, Control, and Computing, Urbana-Champaign, IL, Sep. 2009, pp. 1243–1249.

14. K. V. Rashmi, N. B. Shah, and P. V. Kumar, 「Optimal Exact-Regenerating Codes for Distributed Storage at the MSR and MBR Points via a Product-Matrix Construction,」 IEEE Trans. Inf. Theory, vol. 57, no. 8, pp. 5227–5239, 2011.

15. Y. Hu, H. C. H. Chen, P. P. C. Lee, and Y. Tang, 「NCCloud: applying network coding for the storage repair in a cloud-of-clouds,」 in Proc. 10th USENIX conference on File and Storage Technologies, San Jose, CA, USA,2012, p. 21.

16. Huang C, Simitci H, Xu Y, et al. Erasure Coding in Windows Azure Storage. in: Proceedings of USENIX Annual Technical Conference (ATC), Boston, MA, USA, June, 2012, USENIX.

17. Hu Y, Li X, Zhang M, et al. Optimal repair layering for erasure-coded data centers: From therory ot practive. ACM Transactions on Storage (TOS), 2017, 13(4):33.

18. Rashmi K, Nakkiran P, Wang J, et al. Having Your Cake and Eating It Too: jonintly Optimal Erasure Codes for I/O, Storage, and Network-bandwidth. in: Proceedings of USENIX Conference on File and Storage Technologies (FAST), Santa Clara, CA, USA, February, 2015, USENIX, 81-94.

19. Hou H, Lee P, Shum K, et al. Rack-aware regenerating codes for data centers. IEEE Transactions Information Theory, 2019,65(8):4730-4745.

20. Sathiamoorthy M, Asteris M, Papailiopoulos D, et al. XORing Elephants: Novel Erasure Codes for Big Data. in: Proceedings of VLDB Endowment. VLDB, March, 2013, 325-336.

21. RASHMI K, SHAN N B, RAMCHANDRAN K. A Piggybacking Design Framework for Read and Download-Efficient Distributed Storage Codes[J]. IEEE Transactions on Information Therory, 2017,63(9):5802-5820.

22. N. B. Shah, K. V. Rashmi, P. V. Kumar, and K. Ramchandran, 「Interference Alignment in Regenerating Codes for Distributed Storage: Necessity and Code Constructions,」 IEEE Trans. Inf. Theory, vol. 58, no. 4, pp. 2134–2158, Apr. 2012.

23. Y.WuandA.G.Dimakis,「Reducingrepairtrafficforerasurecoding-basedstorageviainterferencealignment,」Proc.IEEEInternationalSymposium on Information Theory, Seoul, Korea, June 2009, pp. 2276–2280.

24. C.SuhandK.Ramchandran,「Exact-repairMDScodeconstructionusinginterferencealignment,」IEEETrans.Inf.Theory,vol.57,no.3,pp.1425–1442,Mar. 2011.

25. K. V. Rashmi, N. B. Shah, and P. V. Kumar, 「Optimal Exact-Regenerating Codes for Distributed Storage at the MSR and MBR Points via a Product-Matrix Construction,」 IEEE Trans. Inf. Theory, vol. 57, no. 8, pp. 5227–5239, Aug. 2011.

26. S. J. Lin, W. H. Chung, Y. S. Han, and T. Y. Al-Naffouri, 「A Unified Form of Exact-MSR Codes via Product-Matrix Frameworks,」 IEEE Trans Inf Theory, vol. 61, no. 2, pp. 873–886, Feb 2015.

27. D. Papailiopoulos, A. Dimakis, and V. Cadambe, 「Repair Optimal Erasure Codes through Hadamard Designs,」 IEEE Trans. Inf. Theory, vol. 59, no. 5,pp. 3021–3037, 2013.

28. V.Cadambe,S.A.Jafar,H.Maleki,K.Ramchandran,andC.Suh,「AsymptoticInterferenceAlignmentforOptimalRepairofMDSCodesinDistributedStorage,」 IEEE Trans. Inf. Theory, vol. 59, no. 5, pp. 2974–2987, 2013.

29. I. Tamo, Z. Wang, and J. Bruck, 「Zigzag codes: MDS array codes with optimal rebuilding,」 IEEE Trans. Inf. Theory, vol. 59, no. 3, pp. 1597–1616,2013.

30. Z. Wang, I. Tamo, and J. Bruck, 「On codes for optimal rebuilding access,」 in Proc. 49th Annual Allerton Conference on Communication, Control, and Computing, Sept 2011, pp. 1374–1381.

31. V. R. Cadambe, C. Huang, J. Li, and S. Mehrotra, 「Polynomial length MDS codes with optimal repair in distributed storage,」 in Proc. Forty Fifth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA*, 2011, pp. 1850–1854.

32. Z. Wang, I. Tamo, and J. Bruck, 「Long MDS codes for optimal repair bandwidth,」 in Proc. IEEE International Symposium on Information Theory,Cambridge, MA, USA, 2012, pp. 1182–1186.

33. I. Tamo, Z. Wang, and J. Bruck, 「Access Versus Bandwidth in Codes for Storage,」 IEEE Trans. Inf. Theory, vol. 60, no. 4, pp. 2028–2037, 2014.

34. S. Goparaju, I. Tamo, and A. R. Calderbank, 「An Improved Sub-Packetization Bound for Minimum Storage Regenerating Codes,」 IEEE Trans. on Inf.Theory, vol. 60, no. 5, pp. 2770–2779, 2014.

35. B. Sasidharan, G. K. Agarwal, and P. V. Kumar, 「A high-rate MSR code with polynomial sub-packetization level,」 in Proc. IEEE International Symposium on Information Theory, 2015, pp. 2051–2055.

36. A.S.Rawat,O.O.Koyluoglu,andS.Vishwanath,「Progressonhigh-rateMSRcodes:Enablingarbitrarynumberofhelpernodes,」in Proc.Information Theory and Applications Workshop, La Jolla, CA, USA, 2016, pp. 1–6.

37. S. Goparaju, A. Fazeli, and A. Vardy, 「Minimum Storage Regenerating Codes for All Parameters,」 IEEE Trans. Inf. Theory, vol. 63, no. 10, pp.6318–6328, 2017.

38. G. K. Agarwal, B. Sasidharan, and P. V. Kumar, 「An alternate construction of an access-optimal regenerating code with optimal sub-packetization level,」 in Proc. Twenty First National Conference on Communications, Mumbai, India, 2015, pp. 1–6.

39. N. Alon, 「Combinatorial nullstellensatz,」 Combinatorics, Probability and Computing, vol. 8, no. 1-2, pp. 7–29, 1999.

40. N. Raviv, N. Silberstein, and T. Etzion, 「Constructions of High-Rate Minimum Storage Regenerating Codes Over Small Fields,」 *IEEE Trans. Inf.Theory, vol. 63, no. 4, pp. 2015–2038, 2017.

41. M. Ye and A. Barg, 「Explicit Constructions of High-Rate MDS Array Codes With Optimal Repair Bandwidth,」 IEEE Trans. Inf. Theory, vol. 63, no. 4,pp. 2001–2014, 2017.

42. ——, 「Explicit Constructions of Optimal-Access MDS Codes With Nearly Optimal Sub-Packetization,」 IEEE Trans. Inf. Theory, vol. 63, no. 10, pp.6307–6317, 2017.

43. B. Sasidharan, M. Vajha, and P. V. Kumar, 「An Explicit, Coupled-Layer Construction of a High-Rate MSR Code with Low Sub-Packetization Level,Small Field Size and All-Node Repair,」 CoRR, vol. abs/1607.07335, 2016.

44. J. Li, X. Tang, and C. Tian, 「A generic transformation for optimal repair bandwidth and rebuilding access in MDS codes,」 in Proc. IEEE International**Symposium on Information Theory, Aachen, Germany, June 2017, pp. 1623–1627.

45. S. B. Balaji and P. V. Kumar, 「A tight lower bound on the sub-packetization level of optimal-access MSR and MDS codes,」 CoRR, Accepted at ISIT**2018, vol. abs/1710.05876, 2017.

46. M. Vajha, S. B. Balaji, and P. V. Kumar, 「Explicit MSR Codes with Optimal Access, Optimal Sub-Packetization and Small Field Size for d =k + 1, k + 2, k + 3,」 CoRR, vol. abs/1804.00598, 2018.

47. E.E.Gad,R.Mateescu,F.Blagojevic,C.Guyot,andZ.Bandic,「Repair-optimalMDSarraycodesoverGF(2),」inProc.IEEEInternationalSymposium on Information Theory, Istanbul, Turkey, 2013, pp. 887–891.

48. P. Gopalan, C. Huang, H. Simitci, and S. Yekhanin, 「On the Locality of Codeword Symbols,」 IEEE Trans. Inf. Theory, vol. 58, no. 11, pp. 6925–6934,2012.

49. S. B. Balaji and P. V. Kumar, 「On partial maximally-recoverable and maximally-recoverable codes,」 in Proc. IEEE International Symposium on Information Theory, Hong Kong, 2015, pp. 1881–1885.

50. M. Chen, C. Huang, and J. Li, 「On the maximally recoverable property for multi-protection group codes,」 in IEEE International Symposium on Information Theory, June 2007, pp. 486–490.

51. M. Blaum, J. L. Hafner, and S. Hetzler, 「Partial-MDS Codes and Their Application to RAID Type of Architectures,」 IEEE Trans. Inf. Theory, vol. 59, no. 7, pp. 4510–4519, 2013.

52. G. Calis and O. O. Koyluoglu, 「A General Construction for PMDS Codes,」 IEEE Communications Letters, vol. 21, no. 3, pp. 452–455, 2017.

53. R. Gabrys, E. Yaakobi, M. Blaum, and P. H. Siegel, 「Constructions of partial MDS codes over small fields,」 in Proc. IEEE International Symposium on Information Theory, Aachen, Germany, 2017, pp. 1–5.

54. P. Gopalan, C. Huang, B. Jenkins, and S. Yekhanin, 「Explicit Maximally Recoverable Codes With Locality,」 IEEE Trans. Inf. Theory, vol. 60, no. 9, pp. 5245–5256, 2014.

55. G. Hu and S. Yekhanin, 「New constructions of SD and MR codes over small finite fields,」 in Proc. IEEE International Symposium on Information Theory, Barcelona, Spain, 2016, pp. 1591–1595.

56. J. Chen, K. W. Shum, Q. Yu, and C. W. Sung, 「Sector-disk codes and partial MDS codes with up to three global parities,」 in Proc. IEEE International Symposium on Information Theory, Hong Kong, 2015, pp. 1876–1880.

57. M. Blaum, 「Construction of PMDS and SD codes extending RAID 5,」 CoRR, vol. abs/1305.0032, 2013.

58. M. Blaum, J. S. Plank, M. Schwartz, and E. Yaakobi, 「Construction of Partial MDS and Sector-Disk Codes With Two Global Parity Symbols,」 IEEE Trans. Inf. Theory, vol. 62, no. 5, pp. 2673–2681, 2016.

59. V.LalithaandS.V.Lokam,「Weightenumeratorsandhighersupportweightsofmaximallyrecoverablecodes,」inProc.53rdAnnualAllertonConference on Communication, Control, and Computing, Monticello, IL, USA, 2015, pp. 835–842.

60. G. M. Kamath, N. Prakash, V. Lalitha, and P. V. Kumar, 「Codes With Local Regeneration and Erasure Correction,」 IEEE Trans. Inf. Theory, vol. 60, no. 8, pp. 4637–4660, 2014.

61. Cai H, Miao Y, Schwartz M, et al. On optimal locally repairable codes with super-linear length. IEEE Trans Inform Theroy, 2020, 66: 4853-4868.

62. Chen B, Fang W, Xia S, et al. Constructions of optimal (r,sigma) locally repairabl codes via constacyclic codes. IEEE Trans Commun, 2019, 67: 5253-5263.

63. Chen B, Xia S, Hao J, et al. Constructions of optimal cyclic (r,sigma) locally repairable codes. IEEE Trans Inform Theory, 2018, 64:2499-2511.

64. Fang W, Fu F. Optimal cyclic (r,sigma) locally repairable codes with unbounded length. Finite Fields Appl, 2020,63:101650.

65. A. Agarwal, A. Barg, S. Hu, A. Mazumdar, and I. Tamo, 「Combinatorial alphabet-dependent bounds for locally recoverable codes,」 IEEE Trans. Inf. Theory, vol. PP, no. 99, pp. 1–1, 2018.

66. I. Tamo, A. Barg, S. Goparaju, and A. R. Calderbank, 「Cyclic LRC codes, binary LRC codes, and upper bounds on the distance of cyclic codes,」 CoRR, vol. abs/1603.08878, 2016.

67. S. Goparaju and A. R. Calderbank, 「Binary cyclic codes that are locally repairable,」 in Proc. IEEE International Symposium on Information Theory, Honolulu, HI, USA, 2014, pp. 676–680.

68. A. Zeh and E. Yaakobi, 「Optimal linear and cyclic locally repairable codes over small fields,」 in Proc. IEEE Information Theory Workshop, Jerusalem, Israel, 2015, pp. 1–5.

69. I. Tamo, A. Barg, and A. Frolov, 「Bounds on the Parameters of Locally Recoverable Codes,」 IEEE Trans. Inf. Theory, vol. 62, no. 6, pp. 3070–3083, 2016.

70. A. Barg, I. Tamo, and S. Vldu, 「Locally Recoverable Codes on Algebraic Curves,」 IEEE Trans. Inf. Theory, vol. 63, no. 8, pp. 4928–4939, 2017.

71. X. Li, L. Ma, and C. Xing, 「Construction of asymptotically good locally repairable codes via automorphism groups of function fields,」 CoRR, vol. abs/1711.07703, 2017.

72. M.Y.NamandH.Y.Song,「BinaryLocallyRepairableCodesWithMinimumDistanceatLeastSixBasedonPartialt-Spreads,」IEEECommunications Letters, vol. 21, no. 8, pp. 1683–1686, Aug 2017.

73. N. Silberstein and A. Zeh, 「Optimal binary locally repairable codes via anticodes,」 in Proc. IEEE International Symposium on Information Theory, Hong Kong, 2015, pp. 1247–1251.

74. J. Hao, S. T. Xia, and B. Chen, 「Some results on optimal locally repairable codes,」 in Proc. IEEE International Symposium on Information Theory, Barcelona, Spain, 2016, pp. 440–444.

75. M. Shahabinejad, M. Khabbazian, and M. Ardakani, 「A Class of Binary Locally Repairable Codes,」 IEEE Transactions on Communications, vol. 64, no. 8, pp. 3182–3193, 2016.

76. J. Hao, S. T. Xia, and B. Chen, 「On optimal ternary locally repairable codes,」 in Proc. IEEE International Symposium on Information Theory, Aachen, Germany, 2017, pp. 171–175.

77. J. Hao and S. Xia, 「Bounds and Constructions of Locally Repairable Codes: Parity-check Matrix Approach,」 CoRR, vol. abs/1601.05595, 2016. X. Li, L. Ma, and C. Xing, 「Optimal locally repairable codes via elliptic curves,」 CoRR, vol. abs/1712.03744, 2017.

78. KMM,et,al：An Efficient Piggybacking Design Framework with Sub-packetization l