Outlier Detection

Generalized ESD Test

資料集：\(\left\{ x_{1}, x_{2}, \ldots, x_{n} \right\}\)

原假設 \(H_{0}\)：資料集中不存在異常值。

備擇假設 \(H_{1}:\) 最多存在 \(r\) 個異常值。

計算統計量：

其中，\(\bar{x}\) 為樣本均值，\(s\) 為樣本標準差。

移除使得 \(x_{i} - \bar{x}\) 最大的 \(x_{i}\)，在剩餘的 \((n - 1)\) 個 sample 上重新計算 \(R_{i}\)。重複此過程，得到 \(R_{1}, R_{2}, \ldots, R_{r}\)。

令顯著性水平為 \(\alpha\)，對於 \(i = 1, 2, \ldots, r\)，分別計算：

以上，\(t_{p, v}\) 是自由度為 \(v\) 的 t-distribution 的 \(100p\) 分位點，其中：

根據 Rosner 的資料模擬，該假設檢驗方法在樣本量 \(n \geq 25\) 時非常精確，在 \(n \geq 15\) 時較為精確。

程式碼實現如下：

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.stats as stats

y = np.random.random(100)
x = np.arange(len(y))

plt.scatter(x, y)
plt.show()

y[14] = 9
y[83] = 10
y[44] = 14

plt.scatter(x, y)
plt.show()

def test_stat(y, iteration):
    stdev = np.std(y)
    avg_y = np.mean(y)
    abs_val_minus_avg = abs(y - avg_y)
    max_of_deviations = max(abs_val_minus_avg)
    max_ind = np.argmax(abs_val_minus_avg)
    cal = max_of_deviations / stdev
    print(f'Test Statistics Value(R{iteration}) : {cal}')
    return cal, max_ind 

def calc_critical(size, alpha, iteration):
    t_dist = stats.t.ppf(1 - alpha  / (2 * size), size - 2)
    numerator = (size - 1) * np.sqrt(np.square(t_dist))
    denominator = np.sqrt(size) * np.sqrt(size - 2 + np.square(t_dist))
    critical = numerator / denominator
    print(f'Critical Value(lambda{iteration}) : {critical}')
    return critical

def check_values(R, C, inp, max_index, iteration):
    if R > C:
        print('{} is an outlier. R{} > λ{}: {:.4f} > {:.4f} \n'.format(inp[max_index],iteration, iteration, R, C))
    else:
        print('{} is not an outlier. R{}> λ{}: {:.4f} > {:.4f} \n'.format(inp[max_index],iteration, iteration, R, C))


def ESD_Test(input_series, alpha, max_outliers):
    stats = []
    critical_vals = []
    for iterations in range(1, max_outliers + 1):
        stat, max_index = test_stat(input_series, iterations)
        critical = calc_critical(len(input_series), alpha, iterations)
        check_values(stat, critical, input_series, max_index, iterations)
        input_series = np.delete(input_series, max_index)
        critical_vals.append(critical)
        stats.append(stat)
        if stat > critical:
            max_i = iterations
    print('H0:  there are no outliers in the data')
    print('Ha:  there are up to 10 outliers in the data')
    print('')
    print('Significance level:  α = {}'.format(alpha))
    print('Critical region:  Reject H0 if Ri > critical value')
    print('Ri: Test statistic')
    print('λi: Critical Value')
    print('')
    df = pd.DataFrame({'i' :range(1, max_outliers + 1), 'Ri': stats, 'λi': critical_vals})
    
    def highlight_max(x):
        if x.i == max_i:
            return ['background-color: yellow']*3
        else:
            return ['background-color: white']*3
    df.index = df.index + 1
    print('Number of outliers {}'.format(max_i))
    
    return  df.style.apply(highlight_max, axis = 1)

ESD_Test(y, 0.05, 7)

Mining Distance-based outliers in near linear time with randomization and a Simple pruning rule

給定特徵空間上的一個距離測度，存在多種不同基於距離的異常值定義，其中三個經典定義為：

1. 異常值為那些使得滿足相互距離小於 \(d\) 的其餘資料點的個數少於 \(p\) 的資料點。

2. 異常值為那些距離它們最近的第 \(k\) 個鄰居的距離最大的 \(n\) 個資料點。

3. 異常值為那些距離它們最近的 \(k\) 個鄰居的平均距離最大的 \(n\) 個資料點。

以上三種定義均存在一定的問題。第一種定義沒有把 「距離的排序」 納入考量，且引數 \(d\) 的值需要進行估計。第二種定義只考慮到 「最近的第 \(k\) 個鄰居「，而忽略了前 \(k-1\) 個更近的鄰居所包含的資訊。第三中定義雖然求的是最近的 \(k\) 個鄰居的平均距離，但是時間複雜度卻上升了。

演演算法如下：

程式碼實現如下：

import numpy as np
import matplotlib.pyplot as plt


# Distance between two points x and y using Euclidean metric.
def distance(x, y):
    return np.sqrt(np.sum((y - x) ** 2))


# Return the maximum distance between point x and a point in Y.
def max_dist(x, Y):
    return max(map(lambda y: distance(x, y), Y))


# Return the k closest examples in Y to x.
def closest(x, Y, k):
    result = []
    for y in list(Y):
        result.append((y, distance(x, y)))
        
    result.sort(key=lambda tup: tup[1], reverse=True)
    
    return set(map(lambda tup: tup[0], result[:min(k, len(result))]))


# D, a set of examples in random order; k, the number of nearest
# neighbors; n, the number of outliers to return.
def find_outliers(D, k, n):
    def score(N, b):
        result = list(map(lambda n: distance(b, n), list(N)))
        result.sort(reverse=True)
        return np.mean(result[:k])

    c = 0
    O = set()
    block_size = len(D) // 5
    pointer = 0
    
    while pointer <= len(D):
        B = D[pointer: min(pointer+block_size, len(D))]
        pointer += block_size
        neighbors = dict.fromkeys(B)
        for i in neighbors.keys():
            neighbors[i] = set()
        for d in D:
            for b in B:
                if b == d:
                    continue
                if len(neighbors[b]) < k or distance(b, d) < max_dist(b, neighbors[b]):
                    neighbors[b] = closest(b, neighbors[b] | {d}, k)
                    if score(neighbors[b], b) < c:
                        B = list(set(B) - {d})
        
        O = set(sorted(list(set(B) | O), reverse=True)[:n])
        c = min([score(O, o) for o in list(O)])

    return O


y = np.random.random(100)
x = np.arange(len(y))

plt.scatter(x, y)
plt.show()

y[14] = 9
y[83] = 10
y[44] = 14

plt.scatter(x, y)
plt.show()

find_outliers(list(y), 3, 3)

Local Outlier Factor (LOF)

異常值識別通常有兩種思路，即基於距離的方法（distance-based approaches）和基於密度的方法（density-based approaches）。前者基於的思想是，觀測到一個距離資料分佈中心非常遠的資料點的概率是極小的，因此這種點可以被視作為一個異常（Mehrotra, 1997）。然而，基於密度的方法也是很重要的，考慮以下情形：

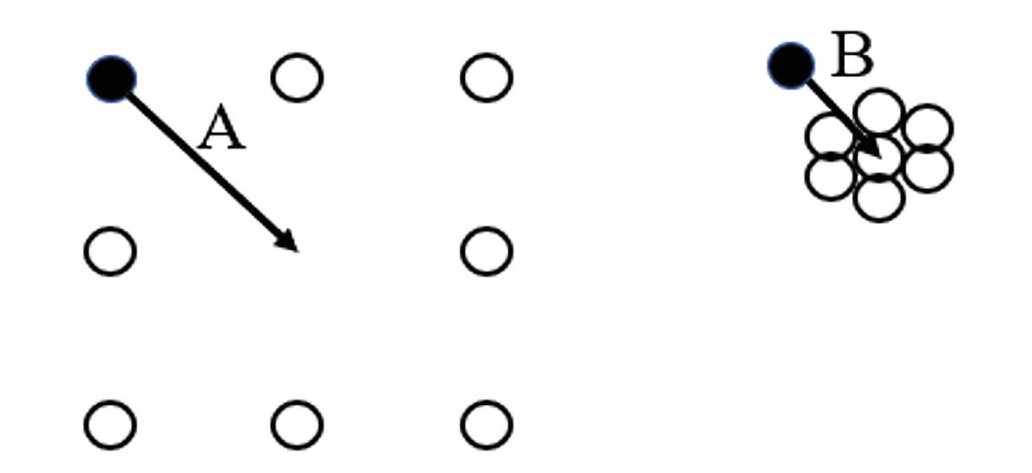
在上方兩圖中，向量 \(A, B\) 分別指向各自資料集的中心，並且如果以距離的視角看待此問題，向量 \(A\) 的模顯然大於向量 \(B\) 的模。然而，相比於向量 \(B\)，相關於向量 \(A\) 的資料點顯然更加均勻地排布在其周圍，或者簡而言之，向量 \(B\) 的座標顯然更像是一個異常值。

在基於密度的識別異常值方法中，我們納入 「鄰域」（neighborhood）的概念，其中一種定義方法是，對於任意一個資料點，給定一個數位 \(n\)，求出資料集中距離它最近的 \(k\) 個點作為它的鄰域。KNN（k-nearest neighbors）演演算法就是對鄰域思想的一種實現，由於演演算法比較基礎這裡按下不表。KNN 演演算法與這裡提到的基於密度的異常值檢驗法的區別是，對於 KNN 演演算法，在確定一個資料點的鄰域後演演算法將停止；然而，對於基於密度的異常值檢驗方法，在確定一個資料點的鄰域後，我們將比較這個資料點的密度與它鄰域中所有資料點的密度。如果相比之下，這個點的密度顯著低於鄰域中其它點的密度，那麼這個點更可能是一個異常值。

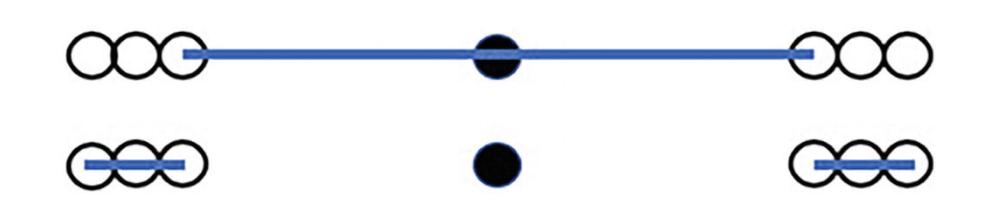
如上圖，假設對於任意一個資料點，我們取距離它最近的兩個點作為其鄰域（即 \(k=2\)）。那麼對於黑點，其鄰域為兩側靠中間的兩個白點，上方的長藍色線段為鄰域覆蓋的範圍；而對於這兩個白點，它們的鄰域卻分別是外側的另外兩個白點，下方的兩段短藍色線段分別為它們鄰域覆蓋的範圍。顯然，黑點的密度遠遠大於其鄰域兩個白點的密度，從圖中恰好體現出，黑點是一個異常值。

Definition. (Reachability Distance)

Reachability Distance 是一個基於密度和鄰域的演演算法，在計算它之前首先要確定一個鄰域的範圍。如下例，假設 \(k=5\)：

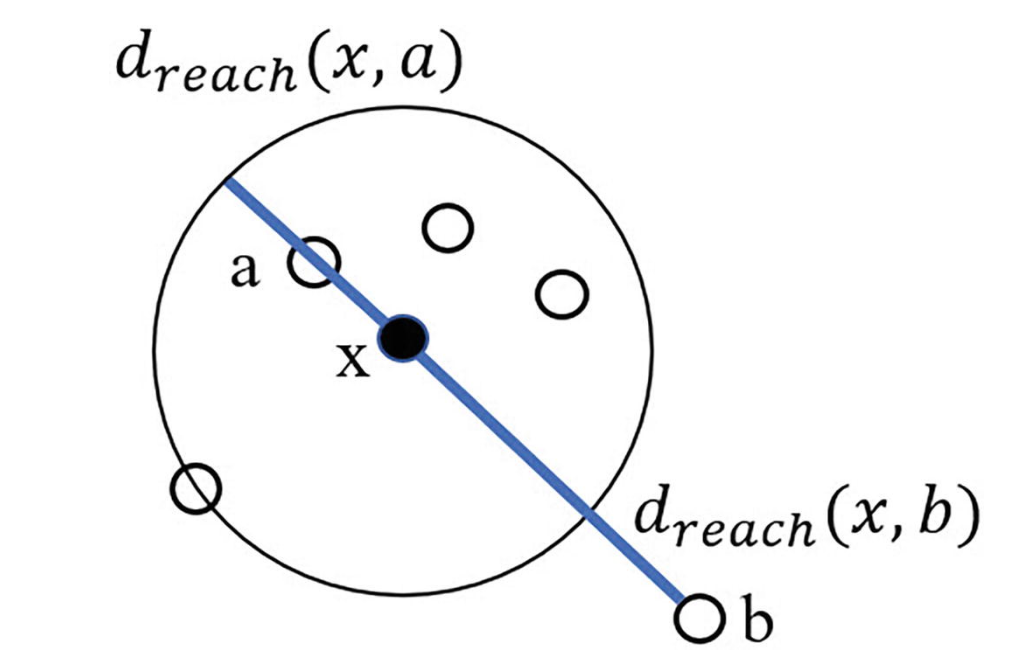
對於資料點 \(x\)，鄰域範圍 \(k=5\)，我們可以確定資料集中距離 \(x\) 最近的五個點（在圖中即為黑點 \(x\) 與除 \(b\) 之外的所有白點，這裡的假設是 \(x\) 也可以作為它自身的鄰近點）。注意到，點 \(b\) 不在 \(x\) 的鄰域中。

我們按照以下方式定義 Reachability Distance：

• 對於在 \(x\) 鄰域之外的點 \(p\)，Reachability Distance 為 \(x\) 與 \(p\) 之間的實際距離。
• 對於在 \(x\) 鄰域之內的點 \(p\)，Reachability Distance 為 \(x\) 與 資料集中距離 \(x\) 第 \(k\) 近的點之間的距離。

在上圖中，圓上的白點為距離 \(x\) 第五近的點（包括 \(x\) 自身），設這個點為 \(o\)，那麼對於圓內任意一點，定義點 \(x\) 到它的 Reachability Distance 皆為圓的半徑，即 \(d(x, o)\)。而對於圓外任意一點，例如點 \(b\)，點 \(x\) 到點 \(b\) 的 Reachability Distance 即為它們的實際距離 \(d(x, b)\)。

換言之，對於目標點 \(x\)，設資料集中距離 \(x\) 第 \(k\) 近的點為 \(o\)，設它到資料集中另外一點 \(p\) 的 Reachability Distance 為 \(d_{reach}(x, p)\)，那麼 \(d_{reach}(x, p)\) 的數學表示式為：

Definition. (Average Reachability Distance)

對於目標點 \(x\)，它的 Average Reachability Distance 定義為 \(x\) 到資料集中除 \(x\) 外所有資料點的平均 Reachability Distances。即，假設資料集為 \(D\)，且 \(|D| = N\)，那麼 Average Reachability Distance 定義為：

對於目標點 \(x\)，它的 Average Reachability Distance 衡量了我們為了尋找 \(x\) 的相似點所需要移動的平均距離。

Definition. (Local Average Reachability Distance)

相似地，對於目標點 \(x\)，假設它的鄰域為 \(S_{x}\)，且 \(|S_{x}| = k\)，那麼它的 Local Average Reachability Distance 定義為：

Definition. (Reachability Density)

對於目標點 \(x\)，它的 Reachability Density 定義為它的 Average Reachability Distance 的倒數，即：

若目標點 \(x\) 的 Average Reachability Distance 越大，說明我們為了尋找與 \(x\) 相似的點所需要移動的平均距離越大，則 \(x\) 的 Reachability Density 越小。

Definition. (Local Reachability Density)

相似地，對於目標點 \(x\)，它的 Local Reachability Density 定義為它的 Local Average Reachability Distance 的倒數，即：

Definition. (Local Outlier Factor)

對於目標點 \(x\)，它的 Local Outlier Factor 定義為：資料集 \(D\) 中除 \(x\) 以外的所有資料點的平均 Local Reachability Density 與 點 \(x\) 的 Local Reachability Density 的比值，即：

Connectivity-Based Outlier Factor

上文介紹的 Local Outlier Factor 的確存在一些實踐中的缺陷，最大的缺陷是，異常值並不一定存在於 「低密度」 區域，如下圖：

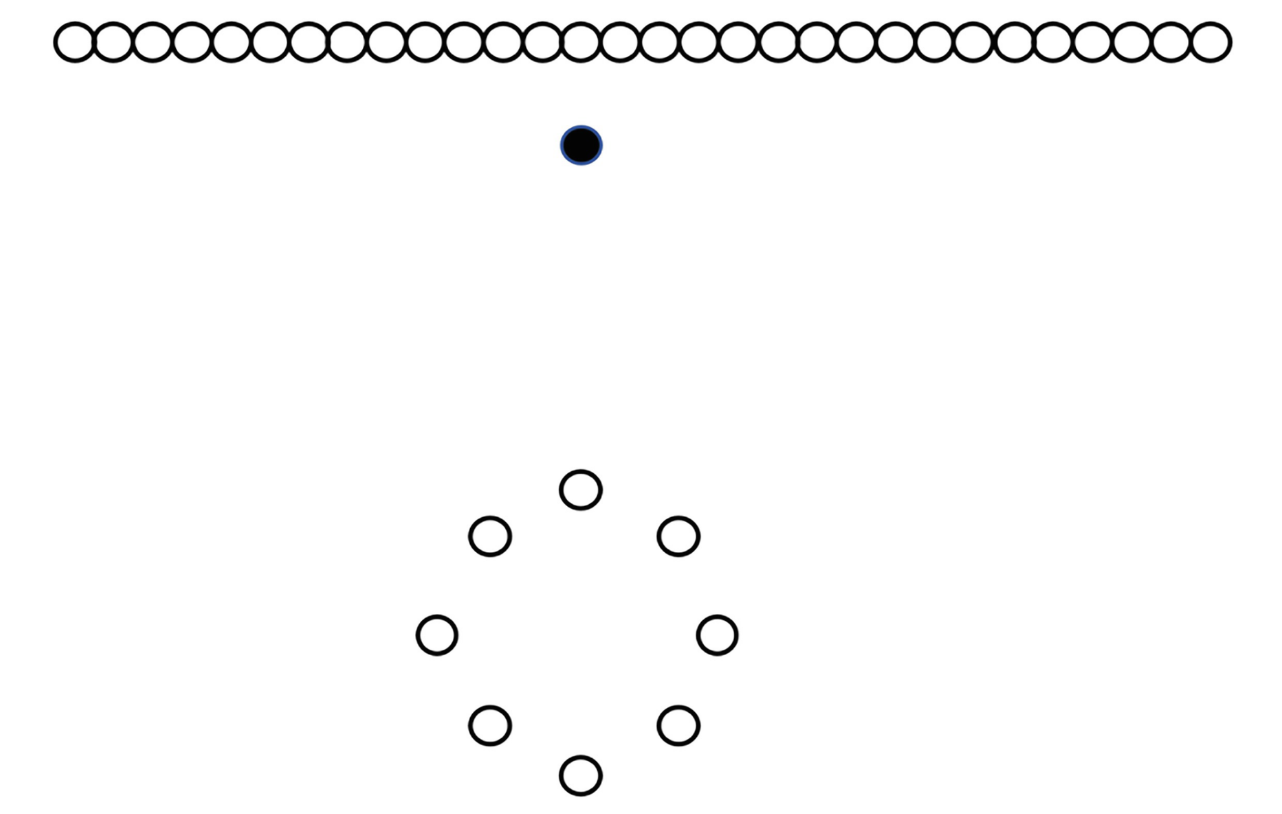
此處，顯然上方與下方的白點分別構成兩簇，黑點即為異常值。然而，如果我們應用 LOF 演演算法且將黑點判別為一個異常點，那麼下方的白色簇將全部歸為異常點，因為該簇中點與點的距離相對較大。

Connectivity-Based Outlier Factor (COF) 是另一種基於密度的聚類方法，並且能夠解決上述 LOF 存在的問題。它向 density 中新增了 isolativity 的概念，即，一個點與其它點的聯絡程度。在上圖中，下方構成圓形的白色點彼此之間相互連線，而黑色點卻並不屬於任何已存在的規律模式（直線或圓），因此，黑點是一個異常值。

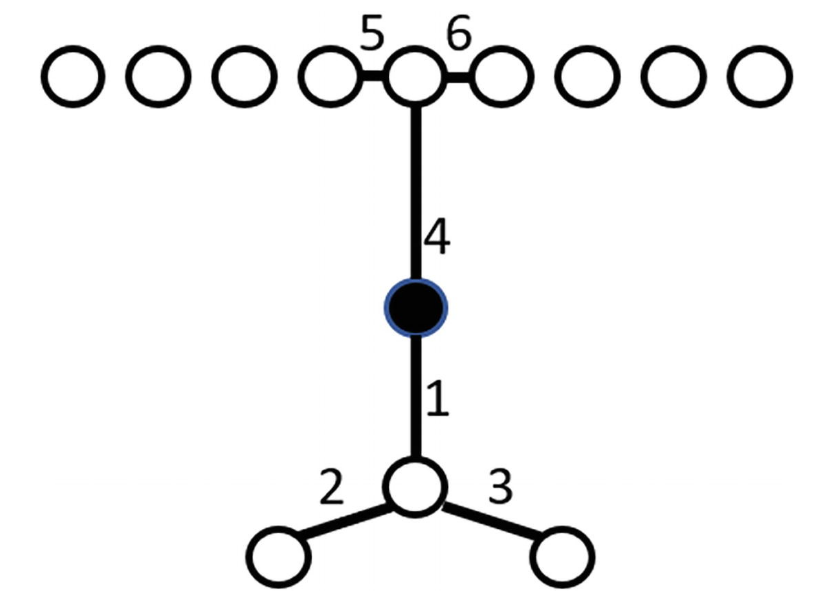
對於上圖這個例子，我們介紹這樣一種演演算法。對於任意一個給定的資料點， 例如圖中黑點，找到與之最相鄰的點，以路徑連線它們並標記為路徑 \(1\)（如圖所示）。將黑點與新連線的點視作一個整體，在所有未與它們相連的點中找到與之相鄰的最近的點，再將它們連線並標記為路徑 \(2\)（如圖所示）。重複這種操作，直到達到最初設定的所需搜尋的點的數量為止。

在建立好上述連線之後，我們可以進行權重運算得到 COF 的值，對於更早的路徑（例如路徑 \(1\) 早於 路徑 \(2\)）賦予更大的權重，更高的 COF 值代表這個點更有可能是一個異常值。

Local Outlier Correlation Integral (LOCI)

Local Outlier Correlation Integral 是一個類似於 LOF 和 COF 的基於密度的異常值檢測法。一個最主要的區別在於，LOCI 提供了一種自動判別一個資料點是否為異常值的方法，這意味著我們無需提供資料以外的任何資訊（Papadimitriou, 2002）。對於 LOF 與 COF，前者我們需要先行規定一個鄰域大小，後者我們需要先行規定搜尋點的數量。相比之下，LOCI 並不需要提前規定鄰域的範圍，它採用了一種測度 \(alpha(\alpha)\) 以表示鄰域的大小，其中 \(\alpha \in (0, 1)\)，預設值 \(\alpha = 0.5\)。

除去 \(\alpha\)，我們還需要一個變數 \(r\)，以代表樣本鄰域（sampling neighborhood）的距離，所謂樣本鄰域即對於一個給定的點，我們用來與之比較的點集。具體來說，我們基於一個半徑為 \(\alpha \cdot r\) 的有界超球，也被稱為 counting neighborhood，通過確定在超球範圍內相鄰點的數量來判斷一個點是否為異常點。

我們令資料集為 \(S = \left\{ p_{1}, p_{2}, \ldots \right\}\)，令資料點 \(p_{i}, p_{j}\) 間的距離為 \(d(p_{i}, p_{j}) \geq 0\)，其中度量 \(d\) 可以任意選取，但除去非負性，還必須滿足度量（metric）的基本三定義，即：

Definition. \(r-neighbors\)

對於給定點 \(p_{i} \in S\)，定義其 \(r-neighbors\) 為被包含在以 \(p_{i}\) 為中心，以 \(r\) 為半徑的閉球 \(\bar{B}_{r}(p_{i})\) 之中的所有資料點，記作 \(\mathcal{N}(p_{i}, r)\)，即：

其中 \(k\) 為資料的維度。

如上圖所示，在二維平面上，半徑為 \(r\) 的圓代表 sampling neighborhood，半徑為 \(\alpha \cdot r\) 的圓代表 counting neighborhood。我們通過計算在 counting neighborhood 範圍內的資料點的數量，來表示給定資料點周圍的點的聚集擁擠程度。我們對於 sampling neighborhood 中其它每一個點都重複此操作，這樣我們能夠比較給定點與其它點所在範圍的擁擠程度。

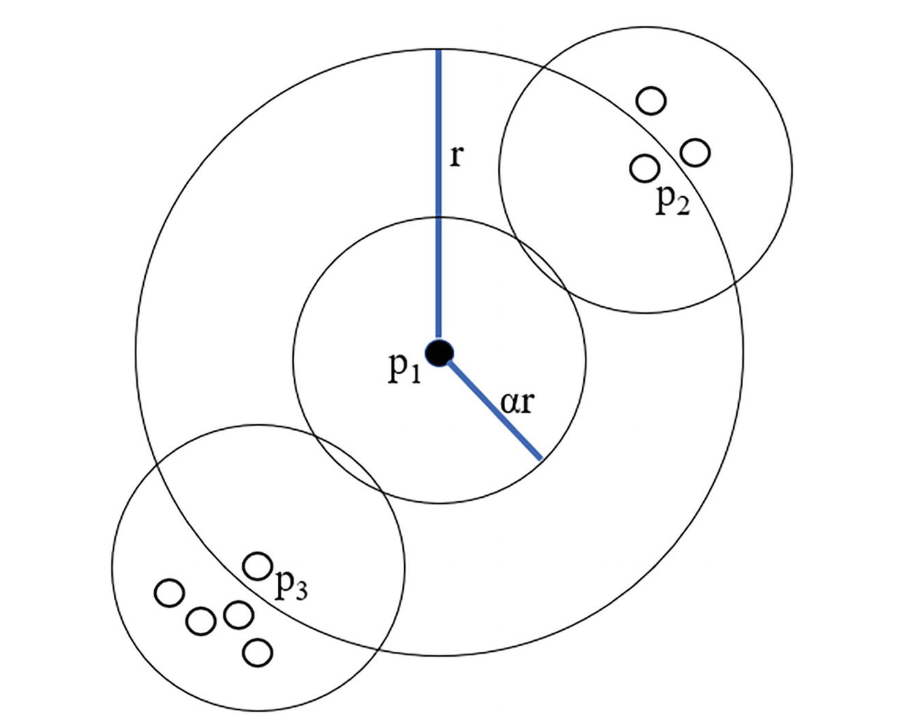
如上圖所示，\(p_{1}\) 是我們選中的點，注意到 \(p_{2}, p_{3}\) 兩點也在 \(p_{1}\) 的 sampling neighborhood 中（半徑為 \(r\) 的圓），同時也分別畫出 \(p_{1}, p_{2}, p_{3}\) 的 counting neighborhood（半徑為 \(\alpha \cdot r\) 的小圓）。在各自的 counting neighborhood 中，我們觀察到 \(p_{1}\) 擁有 \(1\) 個這樣的資料點（即它自身），\(p_{2}\) 擁有 \(3\) 個，\(p_{3}\) 擁有 \(5\) 個。

我們定義以點 \(p_{i}\) 為中心，半徑為 \(r\) 的 \(r-neigbors\) 中所包含點的個數為 \(n(p_{i}, r)\)，即：

則對於點 \(p_{i}\)，其半徑為 \(\alpha \cdot r\) 的 counting neighborhood \(\alpha r - neigbors\) 中包含的點的個數為 \(n(p_{i}, \alpha r)\)。

例如對於上圖：

對於給定的資料點，我們可以計算它的 sampling neighborhood 中的平均 \(\alpha r - neighbors\)，記作 \(\hat{n}(p_{i}, r, \alpha)\)，即：

對於上例，我們有：

Multi-granularity Deviation Factor (MDEF)

多粒度偏離因子（Multi-granularity Deviation Factor）應用上述的公式進行計算：

換言之，我們將給定資料點的 \(\alpha r - neighbors\) 與它 sampling neighborhood 中的平均 \(\alpha r - neighbors\) 進行比較。在上例中，我們有：

定義 \(\sigma_{\hat{n}}(p_{i}, r, \alpha)\) 為資料點 \(p_{i}\) 的 sampling neighborhood 中所有點的 counting neighborhood 中包含點的數量的標準差，即：

在上例中，\(\sigma_{\hat{n}}(p_{1}, r, \alpha)\) 為：

定義 MDEF 的標準差 \(\sigma_{\text{MDEF}}(p_{i}, r, \alpha)\) 為：

在得到 \(MDEF(p_{i}, r, \alpha)\) 的標準差之後，我們需要除 \(\alpha\) 外的另一個引數 \(k_{\sigma}\)，代表我們所取的 MDEF 的標準差的個數，若點 \(p_{i}\) 的 \(MDEF(p_{i}, r, \alpha)\) 值超過 \(k_{\sigma}\) 個 MDEF 的標準差，我們認為它是一個異常值，即：

原論文中 \(k_{\sigma}\) 的預設值為 \(3\)（Papadimitriou, 2002），如此選取的原因參考以下引理。

Lemma. (Deviation probability bounds)

對於任意一個資料集中兩兩點的距離的分佈，以及其中任意一點 \(p_{i}\)，我們有：

Proof.

由 Chebyshev’s inequality，我們有：

切比雪夫不等式是一個相對寬鬆的界，但是它獨立於兩兩距離距離的分佈情況而成立。若資料集中點的兩兩距離的分佈已知，實際的界將收緊。例如，若 neighborhood sizes 服從正態分佈，且我們選取 \(k_{\sigma} = 3\)，根據 Chebyshev’s inequality，大約有 \(\frac{1}{9}\) 的資料點將被視為異常點，但是實際上被視作異常值的點的個數將遠遠小於 \(0.01\)。

Copula-Based Outlier Detection (COPOD)

Copula 是一種提供靈活與通用的生成給定單變數邊際分佈的多元分佈的方法。由於邊際分佈已確定，聯合分佈則能通過這已確定的邊際分佈變換到單位立方體 cube: \([0, 1]^{n}\)​ 上。具體請參考：Copula - 車天健 - 部落格園 (cnblogs.com)。一個資料集中可能包含多個隨機變數，這便存在兩個問題：第一，我們不一定能夠知道各個變數的分佈，例如一個由 \(X \times Y\) 生成的資料集，\(X \sim N(\mu, \sigma^{2})\)，而 \(Y \sim Beta(\alpha, \beta)\)，在更極端的情況下我們甚至連邊緣分佈的型別都不知道；第二，我們不一定能知道變數之間的相關性，例如，在 」\(\text{身高} \times \text{體重}\)「 的資料集中，粗暴地假設體重獨立於身高是不合理。簡單來說，Copula 允許我們僅僅通過隨機變數 \(X_{1}, X_{2}, \ldots, X_{d}\) 各自的邊緣分佈，來大致描述其聯合分佈 \((X_{1}, X_{2}, \ldots, X_{d})\)。

COPOD 通過擬合 Empirical Copula，由於 Copula 本質是一個多元累積分佈函數，那麼此 Empirical Copula 即是一個 Empirical Cumulative Distribution Function（ECDF，經驗 CDF）。令 \(X\) 是一個 \(d\) 維資料集且擁有 \(n\) 個 observation，我們使用 \(X_{i}\) 表示第 \(i\) 個 observation，\(X_{j}\) 表示第 \(j\) 個維度，\(X_{j, i}\) 來表示第 \(i\) 個 observation 在第 \(j\) 維度上的值。

經驗 CDF \(\hat{F}(x)\) 定義為：

Theorem.

令 \(X\) 為連續隨機變數，其 CDF 為 \(F\)，那麼 \(F_{X}(X) \sim \text{Unif}[0, 1]\)。

Proof.

首先， \(F_{X}\) 為累積分佈函數，則 \(F_{X}(X) \in [0, 1]\)。令 \(Y = F_{X}(X)\)，那麼：

因此 \(F(X) \sim \text{Unif}[0, 1]\)。

Inverse Sampling

我們可以通過均勻分佈以逆變換（inverse transform）生成任意所需的分佈。例如，有均勻隨機變數 \(U \sim \text{Unif}[0, 1]\)，那麼 \(F^{-1}(U)\) 服從於分佈 \(F\)。這有兩種理解方式：

1. 由以上 Theorem. 可知，若 \(X\) 是連續隨機變數且 CDF 為 \(F_{X}\)，那麼 \(F_{X}(X) \sim \text{Unif}[0, 1]\)，則 \(U \sim \text{Unif}[0, 1]\) 同分佈於隨機變數 \(F_{X}(X)\)。因此，\(F_{X}^{-1}(U)\) 同分佈於 \(F_{X}^{-1}(F_{X}(X)) = X\)，服從於分佈 \(F_{X}\)。

2. 令 \(Y = F_{X}^{-1}(U)\)，則：

   \[\begin{align*} P(Y \leq y) & = P(F_{X}^{-1}(U) \leq y) \\ & = P(F_{X}(F_{X}^{-1}(U)) \leq F_{X}(y)) \qquad (F_{X} \text{ is monotonically increasing}) \\ & = P(U \leq F_{X}(y)) \\ \end{align*} \]

   注意到 \(F_{X}(y)\) 是一個常數，則 \(P(U \leq F_{X}(y)) = F_{U}(F_{X}(y)) = F_{X}(y)\)，因此：

   \[P(Y \leq y) = F_{X}(y) \]

   所以 \(Y = F_{X}^{-1}(U)\) 服從於分佈 \(F_{X}\)。

我們令一個 \(d\) 維 copula: \(C: [0, 1]^{d} \rightarrow [0, 1]\)，為一個隨機向量 \(\vec{U} = (U_{1}, U_{2}, \ldots, U_{d})\) 的 CDF，其中 \(U_{i} \sim \text{Unif}[0, 1], ~ \forall 1 \leq i \leq d\)，記作：

結合上述 Theorem，我們有：

即 Sklar’s Theorem。

對於維度 \(j\)，由 inverse transformation 有：

通過上述 inverse transformation，我們可以得到 empirical copula \(\hat{U}^{i}\)：

結合經驗 CDF 表示式，我們能得到 empirical copula：

通過 COPOD 實現異常值檢驗一共分為三個步驟：

1. 根據資料集 \(X = ( X_{1, i}, X_{2, i}, \ldots, X_{d, i}), ~ 1 \leq i \leq n\) 計算 ECDF（經驗 CDF），對於任意資料點，ECDF 給出在統計經驗上隨機變數取值將小於這個點的概率。

2. 通過上述生成的 ECDF，得出 Empirical Copula Function，從而將隨機變數的聯合概率分佈轉換為邊緣分佈。

3. 使用上述得到的 Empirical Copula Function 估計尾部概率（Tail Probability），即 \(\forall x_{i}: ~ F_{X}(\vec{x_{i}}) = P \big( X_{1} \leq x_{1, i}, \ldots, X_{d} \leq x_{d, i} \big)\)。

Empirical CDF Outlier Detection (ECOD)

假設有獨立同分布生成的樣本資料 \(X_{1}, X_{2}, \ldots, X_{n} \in \mathbb{R}^{d}\)，且資料點維度為 \(d\)，即矩陣資料集 \(\mathbf{X} \in \mathbb{R}^{n \times d}\)。

Definition. Left and Right tail ECDF

Left and right tail ECDF 分別定義為，在某一個維度（例如 \(j\)）上的傳統 CDF 以及 survival function，即對於 \(z \in \mathbb{R}\)：

Definition. Sample Skewness Coefficient

對於某一個維度（例如 \(j\)），這個維度上的 sample skewness coefficient 定義為：

其中 \(\overline{X^{(j)}} = \frac{1}{n} \sum\limits_{i=1}^{n}X_{i}^{(j)}\) 為第 \(j\) 個特徵（維度）的樣本均值。

Definition. Aggregated Tail Probability

對於資料點 \(X_{i} \in \mathbf{X}\) ，定義其以下三種 aggregated tail probability：

Definition. Outlier Score

對於資料點 \(X_{i} \in \mathbf{X}\) ，定義其 outlier score 為以上三種 aggregated tail probability 的最大值：

程式碼實現如下：

import numpy as np

class ECOD(object):

    def __init__(self, data: np.array):

        if len(data.shape) == 1:
            data = data.reshape(-1, 1)

        self.data = data
        self.size, self.dim = self.data.shape

        for p in self.data:
            try:
                assert len(p) == self.dim
            except:
                raise AssertionError("Sample dimensions should be identical.")


    def ecdf(self, x, d: int) -> dict:

        try:
            assert 0 <= d < self.dim
        except:
            raise AssertionError("Incorrect dimension appointed.")

        left = np.sum(self.data[:, d] <= x) / self.size

        right = np.sum(self.data[:, d] >= x) / self.size

        return {"left": left, "right": right}


    def skewness(self, d: int) -> float:

        try:
            assert 0 <= d < self.dim
        except:
            raise AssertionError("Incorrect dimension appointed.")

        avg = np.mean(self.data[:, d])
        nominator = np.mean((self.data[:, d] - avg) ** 3)
        denominator = np.power((np.sum((self.data[:, d] - avg) ** 2) / (self.size - 1)), 1.5)

        return nominator / denominator


    def aggregate(self, p: np.array) -> dict:

        left, right, auto = [], [], []

        for j in range(self.dim):
            prob = self.ecdf(x=p[j], d=j)
            left.append(np.log(prob["left"]))
            right.append(np.log(prob["right"]))

            if self.skewness(j) < 0:
                auto.append(np.log(prob["left"]))
            else:
                auto.append(np.log(prob["right"]))

        return {"left": -np.sum(left), "right": -np.sum(right), "auto": -np.sum(auto)}


    def score(self, p) -> float:
        return np.max(list(self.aggregate(p=p).values()))


    def execute(self, onum: int):
        scores = list(map(lambda p: self.score(p=p), self.data))
        idx = np.argsort(scores)[::-1][:onum]

        return self.data[idx]